Ứng dụng mạch khuếch đại thuật toán

Bài này nêu lên một số ứng dụng tiêu biểu của các linh kiện tích hợp mạch rắn - Mạch khuếch đại thuật toán. Trong bài có sử dụng các sơ đồ đơn giản hóa, và người đọc nên lưu ý rằng nhiều chi tiết như tên của linh kiện, số thứ tự chân ra và nguồn cung cấp không được thể hiện trong hình.

Các điện trở sử dụng trong các sơ đồ thường được ghi nhận giá trị trên đơn vị là kΩ. Các điện trở có dải < 1 kΩ có thể gây ra dòng điện quá mức và có khả năng phá hỏng linh kiện. Các điện trở có dải >1 MΩ có thể gây ra các tạp âm nhiệt và làm cho mạch vận hành kém ổn định ứng với dòng định thiên đầu vào.

Ghi chú: Một điều quan trọng cần lưu ý là các công thức dưới đây giả định rằng chúng ta sử dụng các mạch khuếch đại thuật toán lý tưởng. Điều đó có nghĩa là khi thiết kế thực tế các mạch này cần phải tham khảo thêm một số tài liệu chi tiết khác.

Ứng dụng mạch thuật toán

Mạch khuếch đại đơn

Mạch khuếch đại vi sai

Bài chi tiết: Khuếch đại vi sai

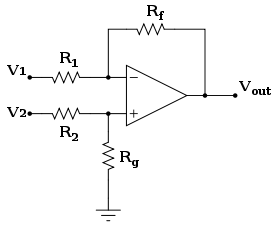
Mạch điện này dùng để tìm ra hiệu số, hoặc sai số giữa 2 điện áp mà mỗi điện áp có thể được nhân với một vài hằng số nào đó. Các hằng số này xác định nhờ các điện trở.

Thuật ngữ "Mạch khuếch đại vi sai" không được nhầm lẫn với thuật ngữ "Mạch vi phân" cũng trong bài này.

$V_{\mathrm {out} }=V_{2}\left({\left(R_{\mathrm {f} }+R_{1}\right)R_{\mathrm {g} } \over \left(R_{\mathrm {g} }+R_{2}\right)R_{1}}\right)-V_{1}\left({R_{\mathrm {f} } \over R_{1}}\right)$

• Tổng trở vi sai $Z_{\mathrm {in} }$ (giữa 2 chân đầu vào) = $R_{1}+R_{2}$

Hệ số khuếch đại vi sai

Nếu $R_{1}=R_{2}$ và $R_{\mathrm {f} }=R_{\mathrm {g} }$,

$V\mathrm {out} =A(V_{\mathrm {2} }-V_{\mathrm {1} })$ và $A=R_{\mathrm {f} }/R_{\mathrm {1} }$

Mạch khuếch đại đảo

Mạch khuếch đại đảo

Dùng để đổi dấu và khuếch đại một điện áp (nhân với một số âm)

$V_{\mathrm {out} }=-V_{\mathrm {in} }(R_{\mathrm {f} }/R_{\mathrm {in} })\!\$

• $Z_{\mathrm {in} }=R_{\mathrm {in} }$ (vì $V_{-}$ là một điểm đất ảo)
• Một điện trở thứ ba, có trị số $R_{\mathrm {f} }\|R_{\mathrm {in} }=R_{\mathrm {f} }R_{\mathrm {in} }/(R_{\mathrm {f} }+R_{\mathrm {in} })$, được thêm vào giữa đầu vào không đảo và đất mặc dù đôi khi không cần thiết lắm, nhưng nó sẽ giảm thiểu sai số do dòng định thiên đầu vào.

Mạch khuếch đại không đảo

Mạch khuếch đại không đảo

Dùng để khuếch đại một điện áp (nhân với một hằng số lớn hơn 1)

$V_{\mathrm {out} }=V_{\mathrm {in} }\left(1+{R_{2} \over R_{1}}\right)$

• $Z_{\mathrm {in} }=\infty$ (thực ra, tổng trở bản thân của đầu vào op-amp có giá trị từ 1 MΩ đến 10 TΩ. Trong nhiều trường hợp tổng trở đầu vào có thể được xem như cao hơn, do ảnh hưởng của mạch hồi tiếp.)
• Một điện trở thứ ba, có giá trị bằng $R_{\mathrm {f} }\|R_{\mathrm {in} }$, được thêm vào giữa nguồn tín hiệu vào $V_{\mathrm {in} }$ và đầu vào không đảo trong khi thực ra không cần thiết, nhưng nó sẽ làm giảm thiểu những sai số do dòng điện định thiên đầu vào.

Mạch đệm điện áp

Mạch theo điện áp

Được sử dụng như một bộ khuếch đại đệm, để giới hạn những ảnh hưởng của tải hay để phối hợp tổng trở (nối giữa một linh kiện có tổng trở nguồn lớn với một linh kiện khác có tổng trở vào thấp). Do có hồi tiếp âm sâu, mạch này có khuynh hướng không ổn định khi tải có tính dung cao. Điều này có thể ngăn ngừa bằng cách nối với tải qua 1 điện trở.

$V_{\mathrm {out} }=V_{\mathrm {in} }\!\$

• $Z_{\mathrm {in} }=\infty$ (thực ra, tổng trở bản thân của đầu vào op-amp có giá trị từ 1 MΩ đến 10 TΩ.)

Mạch khuếch đại cộng đảo

Mạch khuếch đại tổng

Mach được sử dụng để làm phép cộng một số tín hiệu điện áp

$V_{\mathrm {out} }=-R_{\mathrm {f} }\left({V_{1} \over R_{1}}+{V_{2} \over R_{2}}+\cdots +{V_{n} \over R_{n}}\right)$

• nếu $R_{1}=R_{2}=\cdots =R_{n}$, và $R_{\mathrm {f} }$ độc lập thì

$V_{\mathrm {out} }=-\left({R_{\mathrm {f} } \over R_{1}}\right)(V_{1}+V_{2}+\cdots +V_{n})\!\$

• Nếu $R_{1}=R_{2}=\cdots =R_{n}=R_{\mathrm {f} }$

$V_{\mathrm {out} }=-(V_{1}+V_{2}+\cdots +V_{n})\!\$

• Ngõ ra sẽ đổi dấu
• Tổng trở đầu vào $Z_{n}=R_{n}$, cho mỗi đầu vào ($V_{-}$ xem như điểm đất ảo)

Mạch tích phân

Mạch tích phân

Mạch này dùng để tích phân (có đảo dấu) một tín hiệu theo thời gian.

$V_{\mathrm {out} }=\int _{0}^{t}-{V_{\mathrm {in} } \over RC}\,dt+V_{\mathrm {initial} }$

(Trong đó, $V_{\mathrm {in} }$ và $V_{\mathrm {out} }$ là các hàm số theo thời gian, $V_{\mathrm {initial} }$ là điện áp ngõ ra của mạch tích phân tại thời điểm t = 0.)

• Lưu ý rằng cấu trúc của mạch này cũng được xem là mạch lọc thông thấp, một dạng của mạch lọc tích cực.

Mạch vi phân

Mạch vi phân

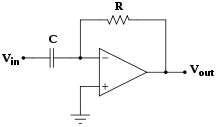
Mạch này để lấy vi phân (có đảo dấu) một tín hiệu theo thời gian.

Thuật ngữ "Mạch vi phân" tránh không nên nhầm lẫn với "mạch khuếch đại vi sai", cũng trong trang này.

$V_{\mathrm {out} }=-RC\left({dV_{\mathrm {in} } \over dt}\right)$

(Trong đó, $V_{\mathrm {in} }$ và $V_{\mathrm {out} }$ là các hàm số theo thời gian)

• Lưu ý rằng cấu trúc của mạch này có thể xem như một mạch lọc thông thường, một dạng của mạch lọc tích cực.

Mạch so sánh

Mạch so sánh

Mạch này để so sánh hai tín hiệu điện áp, và sẽ chuyển mạch ngõ ra để hiển thị mạch nào có điện áp cao hơn.

• $V_{\mathrm {out} }=\left\{{\begin{matrix}V_{\mathrm {S+} }&V_{1}>V_{2}\\V_{\mathrm {S-} }&V_{1}<V_{2}\end{matrix}}\right.$

(Trong đó $V_{\mathrm {s} }$ là điện áp nguồn, và mach sẽ được cấp nguồn từ $+V_{\mathrm {s} }$ và $-V_{\mathrm {s} }$.)

Mạch khuếch đại đo lường

Mạch khuếch đại đo lường

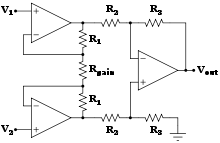
Người ta kết hợp các đặc tính tổng trở vào rất cao, độ suy giảm tín hiệu đồng pha cao, điện áp bù đầu vào thấp và các đặc tính khác để thiết kế mạch đo lường chính xác, độ nhiễu thấp.

• Mạch này được thiết lập bằng cách thêm một mạch khuếch đại không đảo, đệm vào mỗi đầu vào của mạch khuếch đại vi sai để tăng tổng trở vào.
• Vout=v1(hs)