Công (vật lý học)
Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin. |
| Công | |
|---|---|
 Một cầu thủ giao bóng bóng chày tạo ra công lên quả bóng bằng cách tác dụng một lực | |
Ký hiệu thường gặp | A (W trong tiếng Anh - Work (physic)) |
| Đơn vị SI | Joule (J) |
| Trong hệ SI | 1 kg⋅m2/s2 |
Liên hệ với các đại lượng khác | A = F ⋅ s A = τ θ |
| Một phần của chuỗi bài viết về |
| Cơ học cổ điển |
|---|
Công được định nghĩa là hành động được thực hiện trên một đối tượng, gây ra một lực làm dịch chuyển đối tượng đó.
Trong vật lý, công là một đại lượng vô hướng có thể mô tả là tích của lực với quãng đường dịch chuyển mà nó gây ra, và nó được gọi là công của lực. Chỉ có thành phần của lực theo phương chuyển động ở điểm đó thì mới gây ra công. Khái niệm công được đề ra đầu tiên vào năm 1826 bởi nhà toán học người Pháp Gaspard-Gustave de Coriolis.
Đơn vị[sửa | sửa mã nguồn]
Đơn vị SI của công là joule (J), được định nghĩa là công thực hiện bởi một newton làm dịch chuyển một đoạn có chiều dài một mét. Đơn vị tương đương là newton-mét (N.m) cũng được sử dụng thỉnh thoảng, nhưng điều này có thể gây nhầm lẫn với đơn vị newton-mét dùng cho Mô men.
Các đơn vị không phải SI của công bao gồm erg, foot-pound, foot-poundal, và litre-atmosphere. Những đơn vị khác là mã lực, therm, BTU và Ca-lo. Điều quan trọng phải nhớ là nhiệt lượng và công có cùng đơn vị đo.
Nhiệt năng không được xem xét như là một dạng công, vì năng lượng được truyền cho sự rung của các phân tử chứ không phải là sự dịch chuyển vĩ mô. Tuy nhiên, nhiệt lượng có thể gây ra công bởi sự giãn nở khí trong một xi-lanh như là trong động cơ của xe hơi.
Tính toán toán học[sửa | sửa mã nguồn]
Tính toán công như là "lực nhân đoạn thẳng đi được" chỉ có thể thực hiện trong những trường hợp đơn giản mô tả ở trên. Nếu lực biến thiên, nếu vật chuyển động theo một đường cong, có thể là quay, thì chỉ có phần quỹ đạo của điểm tác dụng lực mới tạo nên công, và chỉ có thành phần của lực song song với phương vận tốc của điểm đó của lực mới gây nên công (công dương khi cùng hướng với vận tốc, âm khi ngược hướng). Thành phần này của lực có thể mô tả như một đại lượng vô hướng gọi là thành phần lực tiếp tuyến (, với là góc giữa vectơ lực và vận tốc). Và sau đây là định nghĩa chung của công:
- Công của lực là tích phân đường của thành phần lực tiếp tuyến theo quỹ đạo của điểm tác dụng lực.
Lực và độ dời[sửa | sửa mã nguồn]
Nếu một lực không đổi theo thời gian tác dụng lên một vật làm vật dịch chuyển tịnh tiến một vectơ độ dời , thì công thực hiện của lực lên vật là tích vô hướng của các vectơ và :
- (1)
với là góc giữa vectơ lực và vectơ độ dời.
Khi mà độ lớn và hướng của lực không đổi, quỹ đạo của vật có thể theo bất kỳ hình dạng nào: công thực hiện là độc lập với quỹ đạo và được xác định bởi chỉ một vectơ độ dời tổng cộng . Một ví dụ dễ thấy là công thực hiện bởi trọng lực - xem hình. Vật rơi xuống theo một đường cong, nhưng công được tính từ , nó cho một kết quả quen thuộc .
Nếu lực gây ra (hay ảnh hưởng) đến sự quay của vật, hay vật không rắn, thì độ dời của điểm mà lực tác dụng được dùng để tính công. Trong trường hợp lực thay đổi theo thời gian, phương trình (1) không thể áp dụng được nữa. Nhưng khả dụng nếu chia chuyển động thành nhiều bước nhỏ, đến mức lực có thể coi xấp xỉ là hằng số trong mỗi bước, và công tổng cộng sẽ là tổng công các bước. Điều này sẽ trả lại một kết quả xấp xỉ, mà nó có thể được cải thiện khi chia nhỏ các bước hơn nữa (vi phân). Và kết quả chính xác thu được là giới hạn toán học của quá trình này, dẫn đến định nghĩa dưới đây.
Định nghĩa chung cho công cơ học được cho bởi tích phân đường sau đây:
- (2)
với:
Phương trình (2) giải thích làm sao một lực khác không có thể thực hiện công bằng không. Trường hợp đơn giản nhất là lực luôn vuông góc với phương chuyển động, tạo nên một tích phân luôn bằng không. Nó xảy ra khi vật chuyển động tròn. Tuy nhiên, kể cả khi nếu tích phân thỉnh thoảng có một giá trị khác không, nó vẫn có thể tích phân ra không nếu thỉnh thoảng nó dương và thỉnh thoảng nó âm.
Sự hiện diện của lực khác không tạo công bằng không minh họa sự khác nhau giữa công và đại lượng liên quan, xung lượng, nó là tích phân của lực theo thời gian. Xung lượng đo sự thay đổi động lượng của vật, một đại lượng vectơ có hướng, trong khi công chỉ phụ thuộc độ lớn của vận tốc. Ví dụ như là một vật chuyển động tròn đều chuyển động được một nửa vòng, thì lực hướng tâm của nó không gây công, nhưng nó tạo một xung lượng khác không.
Mô men và sự quay[sửa | sửa mã nguồn]
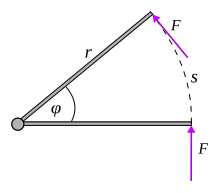
Công thực hiện bởi một mô men lực có thể được tính theo cách tương tự, như là một lực có độ lớn không đổi tác động vuông góc lên một cánh tay đòn. Tích phân tại phương trình (2) cho chiều dài quỹ đạo của điểm đặt lực là cung tròn . Tuy nhiên, cung tròn có thể được tính từ góc quay (đo bằng radian) như là , và tích bằng với mô men . Như vậy, công còn được tính như sau:
với
- là vectơ mô men tác động vào vật;
- là vectơ góc quay của vật quay; và
- là vectơ vận tốc góc của vật quay.
Công và động năng[sửa | sửa mã nguồn]
Theo định lý công-động năng, nếu một hay nhiều ngoại lực tác động lên một vật rắn, làm cho động năng của nó biến thiên từ đến , thì công thực hiện bởi hợp tất cả các lực bằng với độ biến thiên động năng. Trong chuyển động tịnh tiến, định lý có thể mô tả như sau:
với m là khối lượng của vật và v là vận tốc của nó.
Định lý có thể dễ dàng chứng minh cho trường hợp lực tác dụng theo phương chuyển động theo một đường thẳng. Cho những trường hợp phức tạp hơn, ví dụ như một quỹ đạo cong hay lực biến đổi (hay cả hai), chúng ta có thể sử dụng tích phân để lấy kết quả tương đương. Trong cơ học vật rắn, một công thức tính công có thể biến đổi thì động năng bằng cách sử dụng tích phân bậc nhất của định luật 2 Newton.
Để thấy được điều này, hãy khảo sát 1 vật P chuyển động theo một quỹ đạo với một lực tác động lên đó. Định luật 2 Newton cung cấp mối quan hệ giữa lực và gia tốc của vật:
với m là khối lượng của vật.
Nhân vô hướng vận tốc của vật cho mỗi vế của định luật 2 Newton:
Tích phân từ điểm đến điểm ta có:
Vế trái của phương trình là công của lực tác động lên vật dọc theo quỹ đạo từ thời điểm đến thời điểm . Nó còn có thể được viết:
Tích phân này được tính dọc theo quỹ đạo của vật và do đó phụ thuộc vào quỹ đạo.
Vế phải của phương trình tích phân bậc nhất định luật 2 Newton có thể được đơn giản khi sử dụng biểu thức sau:
Biểu thức trên có thể tích phân dễ dàng để chuyển thành động năng:
với động năng của vật được định nghĩa như sau:
Và kết quả là định lý công-động năng cho vật rắn chuyển động:
Công và công suất[sửa | sửa mã nguồn]
Tốc độ công thực hiện bởi một lực (đo bằng joule/giây, hay là watt) là tích vô hướng của một lực (một vectơ) với lại tốc độ thay đổi vectơ độ dời, hay là vectơ vận tốc của điểm đặt lực. Phép nhân vô hướng này giữa lực và vận tốc này được gọi là công suất tức thời.
Cũng như là vận tốc có thể được tích phân theo thời gian để ra quãng đường, thì theo cơ bản của định lý tích phân, tổng công dọc theo một quỹ đạo là tích phân theo thời gian của công suất tức thời tác động dọc theo quỹ đạo của điểm đặt lực.
Hệ quy chiếu[sửa | sửa mã nguồn]
Công thực hiện bởi lực tác động vào một vật phụ thuộc vào cách chọn hệ quy chiếu bởi vì độ dời và vận tốc là phụ thuộc vào hệ quy chiếu mà trong đó chúng ta khảo sát.
Độ biến thiên động năng cũng phụ thuộc vào cách chọn hệ quy chiếu bởi vì động năng là một hàm theo vận tốc. Tuy nhiên, bỏ qua cách chọn hệ quy chiếu, định luật công-động năng vẫn đúng và công thực hiện vẫn bằng độ biến thiên động năng.






































