Hệ thống đầu phiếu
| Hế thống bầu cử |
|
| Politics Portal |
Hệ thống bầu cử cho phép cử tri chọn một trong các giải pháp, thường để chọn ứng viên cho việc quản trị công (Tiếng Anh: public administration hay public office) trong một cuộc bầu cử. Ngoài ra, bỏ phiếu còn dùng để chọn người được trao giải, chọn phương án tối ưu, hay tìm giải pháp cho một vấn đề.
Hệ thống bầu cử chứa đựng những luật lệ cho việc bỏ phiếu hợp lệ, và cách để cho các phiếu bầu được tập trung để có kết quả cuối cùng. Nghiên cứu về các hệ thống bầu cử thì được gọi là thuyết bầu cử, một lĩnh vực trong khoa học chính trị, kinh tế học, hay toán học. Thuyết bầu cử bắt đầu chính thức vào thế kỷ 18 và đang được phát triển.
Các phương diện của hệ thống bầu cử[sửa | sửa mã nguồn]
Một hệ thống bầu cử quy định rõ dạng lá phiếu, tập các lá phiếu cho phép, và phương pháp kiểm phiếu (tallying method), một thuật toán quyết định kết quả. Kết quả có thể là một người thắng cử, hay nhiều người như ở bộ phận lập pháp.
Lá phiếu[sửa | sửa mã nguồn]
Các hệ thống bầu cử có những hình thức khác nhau cho phép cử tri thể hiện ước muốn của mình. Ở hệ thống lá phiếu xếp hạng, cử tri đánh số 1 cho ứng viên thích nhất, số 2 cho vị trí tiếp theo và cứ thế... Hoặc ở hệ thống đa số tương đối cử tri chỉ được phép đánh dấu vào một ứng viên mình thích nhất, trong khi đó ở hệ thống đầu phiếu đồng thuận (approval voting), cử tri có thể chọn bao nhiêu tùy thích. Ở hệ thống khác như đa phiếu tích lũy (cumulative voting) lại cho phép một cử tri bỏ nhiều hơn một phiếu cho một ứng viên.
Ở một số hệ thống bầu cử còn kèm theo các lựa chọn phụ vào lá phiếu như dành chỗ cho cử tri ghi tên ứng cử viên không ở trong danh sách vào lá phiếu, hoặc cho phép không chọn ai trong danh sách.
Trọng lượng lá phiếu[sửa | sửa mã nguồn]
Các cuộc bầu cử thường được tổ chức theo ý tưởng "mỗi người, một phiếu", có nghĩa là mỗi cử tri chỉ có một lá phiếu và chúng đều có giá trị quyết định như nhau. Tuy nhiên, ở nhiều trường hợp điều đó không được đúng. Ví dụ như ở các công ty cổ phần, trọng lượng lá phiếu tùy thuộc vào số lượng cổ phiếu mà cử tri hay cổ đông đó nắm giữ, và chuyển thành "mỗi cổ phần, một lá phiếu". Hoặc vì một cử tri nào đó là thành viên cấp cao hơn của một tổ chức thì lá phiếu của người đó cũng có trọng lượng hơn.
Khu vực bầu cử[sửa | sửa mã nguồn]
Mục đích thường thấy của một cuộc bầu cử là để cho bộ phận lập pháp với nhiều thành viên. Việc này được thực hiện bằng cách tổ chức một cuộc bầu cử và chọn các ứng viên thắng cử từ rất nhiều ứng viên, hoặc bằng cách chia cử tri thành nhiều nhóm ở các khu vực bầu cử khác nhau với các lựa chọn và ứng viên khác nhau.
Một số quốc gia, như Israel, thành lập nghị viện bằng cách tổ chức một hạt bầu cử nhiều người thắng, trong khi các quốc gia như Cộng hòa Ireland hay Bỉ, chia các cuộc bầu cử quốc gia thành các hạt bầu cử nhiều người thắng nhỏ hơn, thế nhưng Mỹ hay Vương quốc Anh chỉ tổ chức các cuộc bầu cử một người thắng (ở từng khu vực) mà thôi.
Phương pháp một người thắng[sửa | sửa mã nguồn]
Hệ thống này có thể được phân loại dựa trên hình thức lá phiếu của nó
Phương pháp tuần tự[sửa | sửa mã nguồn]

Phương pháp bỏ phiếu một người thắng phổ biến nhất hiện nay là hệ thống bầu cử đa số tương đối (plurality, first-past-the-post, hay relative majority). Ở hệ thống này, mỗi cử tri chỉ được bầu cho một ứng viên, và người thắng cử là người nhận được nhiều phiếu bầu nhất, ngay cả khi số phiếu đó nhỏ hơn đa số tuyệt đối (50%).
Phương pháp dồn phiếu (runoff) cho phép đảm bảo người thắng cử do đa số cử tri chọn. Việc chọn hai ứng viên có số phiếu cao nhất cho vòng hai của bầu cử hai vòng (runoff election) cũng là một phương pháp phổ biến nữa. Tuy nhiên, nếu một ứng viên nào đó có số phiếu quá bán thì sẽ không có vòng hai.
Phương pháp lá phiếu ngẫu nhiên là phương pháp mỗi cử tri chỉ chọn một lựa chọn, và mỗi lá phiếu được chọn ngẫu nhiên để quyết định người thắng cuộc. Phương pháp này được dùng phổ biến như là cách chọn một trong những ứng viên có số phiếu cân bằng nhau.
Phương pháp xếp hạng[sửa | sửa mã nguồn]

Còn được biết đến với tên phương pháp bỏ phiếu theo thứ tự ưu tiên (preferential voting methods), phương pháp này cho phép mỗi cử tri xếp hạng các ứng viên theo thứ tự mình thích. Thường thì không phải tất cả các ứng viên được xếp hạng, như vậy, những ứng viên không được xếp hạng được xem như được xếp cuối. Một số nơi còn cho phép cử tri xếp hạng nhiều ứng viên cùng một mức.
Phương pháp đánh giá[sửa | sửa mã nguồn]

Phương pháp cho điểm (score voting) dường như còn uyển chuyển hơn phương pháp xếp hạng, nhưng lại ít được dùng. Ở phương pháp này, cử tri cho điểm mỗi ứng viên, chẳng hạn cho theo chữ số (ví dụ từ 0 đến 100) hoặc ký tự A/B/C/D/E... Như vậy, người có tổng số điểm cao nhất sẽ thắng cử.
Ở phương pháp đầu phiếu đồng thuận (approval voting), cử tri lại có thể bầu cho nhiều ứng viên mà họ thích, và như vậy nó được xem là một dạng khác của phương pháp đánh giá mà mỗi người được chọn được 1 điểm và không được chọn được 0 điểm.
Phương pháp nhiều người thắng cử[sửa | sửa mã nguồn]
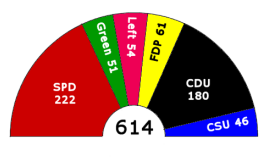
Phương pháp này thường được dùng cho các cuộc bầu cử cơ quan lập pháp. Các ứng viên tham gia trong loại hình bầu cử này thường được quan tâm một cách tổng thể hơn là từng ứng viên cụ thể. Chính vì lý do này, phương pháp nhiều người thắng cử thường được áp dụng cho đại diện tỷ lệ, có nghĩa là nếu một đảng nào đó chiếm x% số phiếu bầu, thì nó cũng sẽ chiếm khoảng chừng ấy phần trăm ghế trong bộ phận lập pháp, hay cụ thể hơn là quốc hội hay nghị viện.
Các phương pháp không theo tỉ lệ và bán tỉ lệ[sửa | sửa mã nguồn]
Nhiều phương pháp đầu phiếu nhiều người thắng cử chỉ là sự mở rộng của phương pháp một người thắng. Ở bỏ phiếu nhóm (bloc voting), đảng dành được nhiều phiếu bầu nhất sẽ thắng cử và chiếm được toàn bộ ghế. Chính vì có xu hướng thắng toàn diện (landslide victory) của nhóm người thắng cử nên phương pháp bầu cử này không tỉ lệ. Có hai phương pháp khác tương tự cho nhiều người thắng là phương pháp bỏ phiếu không chuyển nhượng đơn (Single Non-Transferable Vote, hay SNTV) – cử tri chỉ được bầu cho một ứng viên, và phương pháp đa phiếu tích lũy như được nói ở trên.
Không giống như bỏ phiếu nhóm, các cuộc bầu cử sử dụng phương pháp bỏ phiếu không chuyển nhượng đơn hay đa phiếu tích lũy có thể đạt tính tỷ lệ nếu cử tri sử dụng đầu phiếu chiến thuật (tactical voting) hay việc đề cử chiến lược (strategic nomination).
Chính vì hai phương pháp trên chỉ khuyến khích kết quả có tỷ lệ chứ không bảo đảm điều đó nên chúng được xem là bán tỉ lệ. Còn một số phương pháp khác cũng thuộc dạng bán tỉ lệ là phương pháp hỗn hợp như bỏ phiếu song song.
Phương pháp tỉ lệ[sửa | sửa mã nguồn]
Các phương pháp tỉ lệ theo đúng nghĩa sẽ bảo đảm tính tỷ lệ bằng cách mỗi ứng viên thắng cử sẽ đại diện cho số cử tri tương xứng. Số lượng cử tri này được gọi là hạn ngạch (quota). Ví dụ như, hạn ngạch là 1000 cử tri, thì mỗi ứng viên được bầu phản ánh nguyện vọng của 1000 cử tri đó, trong giới hạn sai số. Chúng ta có thể đo được bằng việc dùng Chỉ số Gallagher (Gallagher Index, least squares index – chỉ số bình phương nhỏ nhất).
Các hệ thống tỉ lệ nhất đang được dùng đều dựa trên nguyên tắc đại diện tỉ lệ theo danh sách đảng (party-list proportional representation). Theo nguyên tắc này, cử tri bầu cho các đảng thay vì cho các ứng viên riêng lẻ. Với mỗi hạn ngạch số phiếu mà một đảng nhận được, tương ứng với một trong những ứng viên của họ nhận được một ghế trong hội đồng lập pháp. Tỉ lệ cử tri được làm tròn để tương ứng với số ghế trong hội đồng lập pháp.
Các phương pháp phân phối số ghế có thể được liệt chung vào phương pháp bình quân cao nhất (highest averages method) và phương pháp số dư lớn nhất (largest remainder method). Phương pháp số dư lớn nhất thiết đặt một hạn ngạch cụ thể dựa trên số cử tri, trong khi phương pháp bình quan cao nhất như phương pháp Sainte-Laguë và phương pháp d'Hondt lại quyết định hạn ngạch trực tiếp bằng cách chia số phiếu mà đảng đó nhận được cho một dãy số. Dãy số này tùy thuộc vào mỗi phương pháp cụ thể.
Phương pháp bán tỉ lệ[sửa | sửa mã nguồn]
Một phương pháp điển hình của phương pháp đầu phiếu bán tỉ lệ là đa phiếu tích lũy (cumulative voting – CV). Phương pháp này là một phương pháp thường dùng ở những nơi cử tri có quyền bỏ phiếu khác nhau như ở các công ty cổ phần dùng một cổ phiếu, một phiếu bầu. Đầu phiếu tích lũy còn được dùng ở phương pháp bầu cử nhiều người thắng như ở bỏ phiếu thành lập ban lãnh đạo công ty.
Tiêu chuẩn đánh giá hệ thống một người thắng[sửa | sửa mã nguồn]
Trên thực tế, các quan điểm về các hệ thống bầu cử bị ảnh hưởng nhiều bởi ảnh hưởng của các hệ thống đó lên các nhóm ủng hộ hay phản đối. Điều này có thể tạo sự so sánh các hệ thống bầu cử khác nhau trở nên khó khăn. Vì thế, để so sánh các hệ thống những ý thức hệ chính trị được độc lập và công bằng, các nhà lý luận bầu cử dùng tiêu chuẩn bầu cử để đánh giá một cách toán học hơn.
Khó có hệ thống đầu phiếu nào thỏa mãn mọi tiêu chuẩn đó. Nhà kinh tế học Kenneth Arrow đã chứng minh "định lý sự bất khả Arrow" (Arrow's impossibility theorem) rằng các đặc điểm tốt của các hệ thống đầu phiếu lại trái ngược nhau. Chính vì lý do này, những người tiến hành bầu cử phải quyết định tiêu chuẩn nào là quan trọng nhất cho các cuộc bầu cử của mình.
- Tiêu chuẩn đa số (Majority criterion) — Có tồn tại bộ phận đa số xếp hạng hay đánh giá một ứng viên nào đó luôn luôn cao hơn các ứng viên khác trong cuộc bầu cử không?
- Tiêu chuẩn đơn nhất (Monotonicity criterion) — Có thể làm cho một ứng viên thắng cử thành bại và biến ứng viên bại thành thắng được hay không?
- Tiêu chuẩn nhất quán (Consistency criterion) — Nếu một khu vực bầu cử được chia làm hai và một ứng viên nào đó đều thắng ở cả hai hạt đó thì người ấy có thắng chung cuộc hay không?
- Tiêu chuẩn tham gia (Participation criterion) — Có phải đi bầu thành thật thì luôn tốt hơn không bầu không?
- Tiêu chuẩn Condorcet hay còn gọi là tiêu chuẩn gà chọi (Condorcet criterion) — Nếu một ứng viên đánh bại từng đối thủ một theo phương pháp Condorcet (đại thể là từng đôi một), thì ứng viên đó có luôn thắng không?
- Tiêu chuẩn chiến bại Condorcet (Condorcet loser criterion) — Nếu một ứng nào đó thua trong tất các ứng viên khác trong cuộc so từng đôi một thì ứng viên đó có luôn thua không?
- Tính độc lập của ứng viên không liên quan (Independence of irrelevant alternatives) — Kết quả có được giữ nguyên sau khi thêm hay bớt các ứng viên không thắng cử hay không?
- Tính độc lập của cùng ứng viên (Strategic nomination, independence of clone candidates) — Kết quả có giống nhau nếu thêm vào chính những ứng viên đã có trong danh sách?
- Tính đối xứng ngược (Reversal symmetry) — Nếu toàn bộ cử tri đảo ngược lựa chọn của mình thì ứng viên thắng lúc đầu có thua không?
- Tiêu chuẩn Smith - (Smith criterion hoặc generalized Condorcet criterion) — Nhóm Smith là nhóm ứng cử viên nhỏ nhất đánh bại mọi ứng cử viên không thuộc nhóm trong cuộc bầu cử hai ứng cử viên theo nguyên tắc đa số. Có phải một trong những ứng cử viên Nhóm Smith luôn chiến thắng?
Bản mẫu:Tiêu chuẩn của hệ thống đầu phiếu
Lịch sử[sửa | sửa mã nguồn]
Tiền dân chủ[sửa | sửa mã nguồn]
Bầu cử đã và dang được dùng như một nhân tố căn bản của một xã hội dân chủ hồi dân chủ Athen từ thế kỷ 6 TCN. Một trong những cuộc bỏ phiếu sớm nhất được ghi lại ở Athen là bỏ phiếu theo nguyên tắc đa số cho chiến thắng không mong đợi vì đấy thật ra là việc tẩy chay để đày người dân mà họ (cử tri) không thích nhất. Hầu hết các cuộc bầu cử trong thời kỳ đầu dân chủ đều dùng thể thức đa số này hoặc chỉ là biến thể của nó. Chỉ có một ngoại lệ, vào thế kỷ 13 bang Venice đã thông qua một cách thức bầu cử mà chúng ta gọi hôm nay là đầu phiếu đồng thuận để bầu Đại hội đồng của họ.[1]


Sự sáng lập lý thuyết bầu cử[sửa | sửa mã nguồn]
Lý thuyết bầu cử trở thành đối tượng của nghiên cứu mang tính học thuật vào khoảng Cách mạng Pháp.[1] Jean-Charles de Borda đề xướng nguyên tắc đếm Bardo vào năm 1770 cho bầu cử các thành viên cho Viện Hàn Lâm Khoa Học Pháp. Phương pháp này bị Marquis de Condorcet bác bỏ và ông này đề nghị phương pháp Condorcet và ông cũng viết về nghịch lý Condorcet.[2]
Sự phát triển hậu 1980[sửa | sửa mã nguồn]
Lý thuyết bầu cử đang tập trung vào các tiêu chuẩn của hệ thống bầu cử ở các hệ thống bầu cử cụ thể. Mọi chi tiết về mặt mạnh hay yếu của một hệ thống bầu cử sẵn sàng được hỗ trợ bởi các tiêu chuẩn đã được định nghĩa trước bằng toán học.
Các nhà khoa học chính trị của thế kỷ 20 đã ấn hành nhiều nghiên cứu về ảnh hưởng của các hệ thống bầu cử đến chọn lựa của cử tri, tới các đảng chính trị,[3][4][5] và tới sử ổn định chính trị.[6][7] Một số ít học giả còn nghiên cứu những hiệu ứng đã làm cho các quốc gia thay đổi hệ thống bầu cử của mình.[8][9][10][11][12] Nicolaus Tideman và Donald G. Saari là hai trong một số nhà lý luận nổi tiếng đã góp phần vào việc cải thiện và đưa ra một số khái niệm mới về bầu cử.
Máy tính đã giúp cho việc ứng dụng các phương pháp Kemeny-Young, cặp xếp hạng (ranked pairs), và Schulze xếp hạng tất cả các lựa chọn từ phổ biến nhất đến ít phổ biến nhất.
Sự phổ cập của Internet cũng đã làm tăng sự quan tam và bầu cử. Không giống như các lĩnh vực toán học khác, hệ thống bầu cử tương đối dễ hiểu đối với những người không chuyên.
Các nghiên cứu về hệ thống bầu cử đã ảnh hưởng đến việc cải cách bầu cử hiện nay, như những đề xuất thay thế đầu phiếu đa số bằng các phương pháp khác ở bầu cử cấp chính quyền. Các địa phương ở Mỹ đã dùng phương pháp chuyển phiếu từ dưới lên (instant-runoff voting) từ năm 2000. Nhiều nước khác như New Zealand, Canada cũng thay thế cho phù hợp hơn. Ngoài ra, vào tháng Chín năm 2007, Đảng Tân Dân Chủ Thống Nhất của Hàn Quốc bắt đầu dùng Hệ thống Bầu cử Di động đầu tiên trên thế giới trong cuộc bầu cử tổng thống sơ bộ của mình.[13] Ngay cả các tổ chức phi chính phủ hiện nay cũng dùng các hệ thống bầu cử.
Xem thêm[sửa | sửa mã nguồn]
- Dân chủ điện tử (e-democracy)
- Cải cách bầu cử (electoral reform)
- Bảng các hệ thống đầu phiếu theo quốc gia
- Hệ thống đếm phiếu
- Máy đầu phiếu
Tham khảo[sửa | sửa mã nguồn]
Tham khảo chung[sửa | sửa mã nguồn]
- Arrow, Kenneth J. (1951, 2nd ed., 1963), Social Choice and Individual Values. New Haven: Yale University Press. ISBN 0-300-01364-7
- Colomer, Josep M. ed. (2004). Handbook of Electoral System Choice. London and New York: Palgrave-Macmillan. ISBN 1-4039-0454-5.Quản lý CS1: văn bản dư: danh sách tác giả (liên kết)
- Cretney, Blake. “Election Methods Resource”. condorcet.org. Truy cập 2005. Đã bỏ qua tham số không rõ
|accessmonthday=(trợ giúp); Kiểm tra giá trị ngày tháng trong:|ngày truy cập=(trợ giúp) - Cranor, Lorrie. “Vote Aggregation Methods”. Declared-Strategy Voting: An Instrument for Group Decision-Making. Truy cập 2005. Đã bỏ qua tham số không rõ
|accessmonthday=(trợ giúp); Kiểm tra giá trị ngày tháng trong:|ngày truy cập=(trợ giúp) - Farrell, David M. (2001). Electoral Systems: A Comparative Introduction. New York: St. Martin's Press. ISBN 0-333-80162-8.
Chú thích[sửa | sửa mã nguồn]
- ^ a b J. J. O'Connor and E. F. Robertson. “The history of voting”. The MacTutor History of Mathematics Archive. Bản gốc lưu trữ ngày 2 tháng 4 năm 2019. Truy cập 2005. Đã bỏ qua tham số không rõ
|accessmonthday=(trợ giúp); Kiểm tra giá trị ngày tháng trong:|ngày truy cập=(trợ giúp) - ^ J. J. O'Connor and E. F. Robertson. “Marie Jean Antoine Nicolas de Caritat Condorcet”. The MacTutor History of Mathematics Archive. Bản gốc lưu trữ ngày 16 tháng 12 năm 2008. Truy cập 2005. Đã bỏ qua tham số không rõ
|accessmonthday=(trợ giúp); Kiểm tra giá trị ngày tháng trong:|ngày truy cập=(trợ giúp) - ^ Duverger 1954
- ^ Rae 1971
- ^ Taagapera and Shugart 1989
- ^ Hermens 1941
- ^ Lijphart 1994
- ^ Lijphart 1985 and Lijphart 1992
- ^ Rokkan 1970
- ^ Rogowski 1987
- ^ Boix 1999
- ^ Cox 1997, pp. 15-16
- ^ UNDP Promote Mobile Phone Voting Lưu trữ 2007-12-04 tại Wayback Machine, KBS Global, Truy cập 28 tháng 9 năm 2007
Đọc thêm[sửa | sửa mã nguồn]
- Boix, Carles 1999. Setting the Rules of the Game: The Choice of Electoral Systems in Advanced Democracies American Political Science Review 93, 609-624.</ref>
- Duverger, Maurice. 1954. Political Parties. New York: Wiley.
- Hermens, Ferdinand A. 1941. Democracy or Anarchy? A Study of Proportional Representation. Notre Dame: University of Notre Dame.
- Lijphart, Arend
- 1985 The Field of Electoral Systems Research: A Critical Survey, Electoral Studies 4:
- 1992 Democratization and Constitutional Choices in Czecho-Slovakia, Hungary and Poland, 1989-1991, Journal of Theoretical Politics 4: 207-223.
- 1994 Electoral Systems and Party Systems: A Study of Twenty-Seven Democracies, 1945-1990. Oxford: Oxford University Press, 1994. ISBN 0-19-828054-8.
- Rae, Douglas W. 1971. The Political Consequences of Electoral Laws. New Haven: Yale University Press.
- Rogowski, Ronald. 1987. Trade and the Variety of Democratic Institutions, International Organization
41: 203-224.
- Rokkan, Stein. 1970. Citizens, Elections, Parties: Approaches to the Comparative Study of the Process of Development. Oslo: Universitetsforlaget.
- Taagapera, Rein and Matthew S. Shugart. 1989. Seats and Votes: The Effects and Determinants of Electoral Systems. New Haven: Yale University Press.
Liên kết ngoài[sửa | sửa mã nguồn]
Tổng quát[sửa | sửa mã nguồn]
- ACE Electoral Knowledge Network Expert site providing encyclopedia on Electoral Systems and Management, country by country data, a library of electoral materials, latest election news, the opportunity to submit questions to a network of electoral experts, and a forum to discuss all of the above
- A handbook of electoral system Design Lưu trữ 2009-12-24 tại Wayback Machine from International IDEA
- Accurate Democracy: electoral and legislative voting rules
- Election methods list A mailing list for technical discussions about election methods.
- Electowiki A wiki that focuses on voting theory.
- National Brainstorming project Lưu trữ 2015-11-01 tại Wayback Machine Canadian site.
- Descriptions of Single-Winner Voting Systems Paper by Warren D. Smith.
- Evaluating Voting Methods Lưu trữ 2006-08-21 tại Wayback Machine by Matt Corks
- Open Directory Project Lưu trữ 2006-06-18 tại Wayback Machine category on voting systems
- OpenSTV Lưu trữ 2009-05-01 tại Wayback Machine Software for computing a variety of voting systems including IRV, STV, and Condorcet.
- Ranked Ballot Voting Methods Lưu trữ 2008-12-16 tại Wayback Machine: tutorial, evaluation, and calculator
- Student's Social Choice by Alex Bogomolny. Illustrates various concepts of choice using Java applets.
- Voting, Arbitration, and Fair Division Lưu trữ 2009-09-12 tại Wayback Machine by Marcus Pivato.
- Voting and Election Reform: election calculator and other resources
- Voting Systems by Paul E. Johnson. A textbook-style overview of voting methods and their mathematical properties.
- U.S. Voting System Analysis Lưu trữ 2008-05-09 tại Wayback Machine
- A New Nation Votes: American Elections Returns 1787–1825 Lưu trữ 2008-07-25 tại Wayback Machine
- Logicracy Lưu trữ 2008-12-20 tại Wayback Machine Freely available on-line referendum engine, competence vs. opinion scatter plots, competence-weighted voting, analysis tools, and fraud reduction methods.
- Criteria by Blake Cretney
- Evaluation of ranked ballot voting methods Lưu trữ 2008-12-16 tại Wayback Machine by Rob LeGrand
- Voting Methods Lưu trữ 2006-05-14 tại Wayback Machine: Tutorial and essays by James Green-Armytage
- Electoral systems and the protection and participation of minorities, report by Minority Rights Group, 2006
- Citizens for Approval Voting
- Center for Range Voting CRV simplified entry page
- Center for Voting and Democracy Advocates using IRV in the United States.
- California LocalParty.Org Advocates proportional elections in local elections.
- condorcet.org Advocates Condorcet voting and provides links to vote-tallying software.
- The De Borda Institute A Northern Ireland-based organisation promoting inclusive voting procedures
- May the Best Man Lose Lưu trữ 2003-10-19 tại Archive.today A Discover article on Approval voting and the Borda Count, by Dana Mackenzie.
- Bầu cử qua mạng xã hội
Tài liệu nghiên cứu[sửa | sửa mã nguồn]
- Analysis and Design of Electoral Systems Lưu trữ 2006-06-23 tại Wayback Machine Proceedings of a seminar at the Mathematical Research Institute at Oberwolfach, Germany.
- Analysis of Democratic Institutions: Structure, Conduct and Performance Lưu trữ 2006-06-23 tại Wayback Machine An article by Roger B. Myerson that analyzes voting systems economically.
- PhD seminar on Choice Theory by Robert Nau.
- Common Voting Rules as Maximum Likelihood Estimators by Vincent Conitzer and Tuomas Sandholm.
- A New Monotonic and Clone-Independent Single-Winner Election Method Lưu trữ 2006-06-23 tại Wayback Machine by Markus Schulze (mirror1 Lưu trữ 2006-02-19 tại Wayback Machine, mirror2). Introduces the Schulze method and its use in the Debian project.
- Hybrid Voting Protocols and Hardness of Manipulation Lưu trữ 2006-06-23 tại Wayback Machine by Edith Elkind and Helger Lipmaa.
- On the impact of indifferent voters on the likelihood of some voting paradoxes Lưu trữ 2006-06-23 tại Wayback Machine by Vincent Merlin and Fabrice Valognes.
- In Praise of Manipulation Lưu trữ 2006-06-23 tại Wayback Machine by Martin van Hees and Keith Dowding. Examines strategic voting from an ethical point of view.
- Universal voting protocol tweaks to make manipulation hard by Vincent Conitzer and Tuomas Sandholm.
- Voting by Adaptive Agents in Multi-candidate Elections Lưu trữ 2006-06-23 tại Wayback Machine by Scott Moser.
- Range Voting Lưu trữ 2009-03-26 tại Wayback Machine by Warren D. Smith. After the mathematical advocacy of Range Voting, there is a good monte-carlo comparison of voting systems in virtual elections, which, despite a rudimentary approach to strategy and polling, gives interesting best-case (honest) and worst-case (overstrategic) social utilities for various systems.
- Safe Votes, Sincere Votes and Strategizing by Rohit Parikh and Eric Pacuit.
