Khoảng cách Manhattan
Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin. |
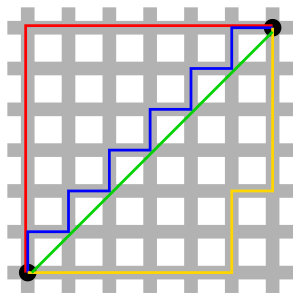
Khoảng cách Manhattan, còn được gọi là khoảng cách L1 hay khoảng cách trong thành phố, là một dạng khoảng cách giữa hai điểm trong không gian Euclid với hệ tọa độ Descartes. Đại lượng này được tính bằng tổng chiều dài của hình chiếu của đường thẳng nối hai điểm này trong hệ trục tọa độ Descartes
Ví dụ, khoảng cách Manhattan giữa hai điểm: có tọa độ và điểm có tọa độ là:





