Ô Wigner-Seitz
Bài này không có nguồn tham khảo nào. (December 2017) |
Ô Wigner–Seitz do Eugene Wigner và Frederick Seitz đặt tên là một loại ô Voronoi được sử dụng trong nghiên cứu vật liệu tinh thể trong vật lý chất rắn.

Tính chất đặc biệt của một tinh thể là các nguyên tử của nó được sắp xếp trong một dãy ba chiều thông thường gọi là mạng tinh thể. Tất cả các tính chất được cho là nguồn gốc các vật liệu tinh thể đều từ cấu trúc bậc cao này. Một cấu trúc như vậy thể hiện tính đối xứng tịnh tiến rời rạc. Xem mô hình như một hệ tuần hoàn, ta cần một công cụ toán học mô tả tính đối xứng và do đó các tính chất vật liệu như một hệ quả của tính đối xứng này. Ô Wigner–Seitz là một định nghĩa để đạt được điều này.
Một ô Wigner–Seitz là một ví dụ của một ô cơ sở, đó là một ô đơn vị chứa chính xác một nút mạng. Nó là locus của các điểm trong không gian gần với nút mạng hơn các nút mạng khác.
Một ô Wigner–Seitz, giống như bất kì ô cơ sở nào, là một hệ cơ bản cho đối xứng tịnh tiến rời rạc của mạng tinh thể. Ô cơ sở của mạng đảo trong không gian xung được gọi là vùng Brillouin.
Định nghĩa[sửa | sửa mã nguồn]
Ô Wigner–Seitz xung quanh một nút mạng được xác định như locus của các điểm trong không gian gần với nút mạng hơn các nút mạng khác.
Nó có thể được chứng minh một cách toán học rằng một ô Wigner–Seitz là một ô cơ sở kéo dài toàn bộ không gian thực mà không bỏ các khoảng trống (gaps) hoặc lỗ trống.
Ô Wigner–Seitz trong không gian mạng đảo được biết như là vùng Brillouin thứ nhất. Nó được tạo ra bằng cách vẽ các mặt phẳng vuông góc với các đoạn nối với các nút mạng gần nhất đến một nút mạng cụ thể, đi qua các trung điểm của các đoạn như vậy.
Cách xây dựng ô[sửa | sửa mã nguồn]
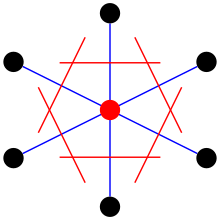
Ô có thể được chọn bằng cách lấy một nút mạng. Sau khi chọn một nút, vẽ các đường thẳng đến tất cả các nút mạng gần nhất. Tại trung điểm của mỗi đường, vẽ đường thẳng khác vuông góc với mỗi tập hợp các đường thẳng đầu tiên.
Trong trường hợp của mạng tinh thể ba chiều, vẽ một mặt phẳng vuông góc tại trung điểm các đường giữa các nút mạng. Bằng cách này, diện tích (hoặc thể tích) nhỏ nhất được vẽ theo cách này và được gọi là ô cơ sở Wigner-Seitz. Tất cả diện tích (hoặc không gian) trong mạng tinh thể được lấp đầy bởi các ô cơ sở này và sẽ không có khoảng hở.
 |
 |
Khái niệm toán học tổng quát[sửa | sửa mã nguồn]
Khái niệm toán học tổng quát thể hiện trong ô Wigner-Seitz thường được gọi là ô Voronoi, và phần mặt phẳng các ô này cho một tập hợp các điểm cho trước được biết đến là một giản đồ Voronoi. Mặc dù bản thân ô Wigner-Seitz không quan trọng lắm trong không gian thực, nhưng nó lại cực kỳ quan trọng trong không gian mạng đảo. Ô Wigner-Seitz trong không gian mạng đảo được gọi là vùng Brillouin, chứa thông tin về vật liệu sẽ là chất dẫn điện hay chất cách điện.
