Phương trình tham số

Trong toán học, phương trình tham số xác định bởi hệ các hàm số của một hoặc nhiều biến độc lập gọi là các tham số.^[1] Phương trình tham số thường được sử dụng để biểu diễn các tọa độ của các điểm thuộc đối tượng hình học như đường cong hoặc bề mặt, mà khi đó các đối tượng này được gọi là biểu diễn theo tham số hoặc tham số hóa.^[1]^[2]^[3]

Ví dụ, phương trình

{\begin{aligned}x&=\cos t\\y&=\sin t\end{aligned}}

là dạng biểu diễn bằng tham số của đường tròn đơn vị, với t là tham số: Một điểm (x, y) nằm trên đường tròn đơn vị nếu và chỉ nếu tồn tại giá trị t thỏa mãn hai phương trình trên. Thỉnh thoảng phương trình tham số cho ánh xạ từ tập xác định nhiều biến vào miền vô hướng được kết hợp thành một phương trình tham số duy nhất của vectơ:

(x,y)=(\cos t,\sin t).

Nói chung biểu diễn hàm bằng phương trình tham số không duy nhất, cùng một hàm số có nhiều cách biểu diễn bằng cách tham số khác nhau.^[1]

Ngoài đường cong và các bề mặt, phương trình tham số có thể biểu diễn cho đa tạp và đa tạp đại số có số chiều cao hơn, với số các tham số độc lập bằng số chiều của đa tạp, và số các phương trình bằng số chiều của không gian trong đó đang xét tới đa tạp hoặc đa tạp đại số (đối với đường cong phẳng số chiều là một và cần một tham số, đối với mặt hai chiều cần hai tham số biểu diễn, vv.).

Phương trình tham số hay được sử dụng trong lý thuyết động học, trong đó quỹ đạo của một đối tượng được biểu diễn bằng phương trình theo thời gian, với thời gian chính là tham số. Theo cách biểu diễn này, một tham số được gán ký hiệu là t; ngoài ra các tham số có thể biểu diễn cho các đại lượng vật lý khác (như các biến hình học) hoặc lựa chọn một cách tùy ý sao cho phù hợp. Phương pháp tham số hóa là không duy nhất; có nhiều hơn một tập phương trình tham số có thể sử dụng để biểu diễn cùng một đường cong.^[4]

Ứng dụng[sửa | sửa mã nguồn]

Động học[sửa | sửa mã nguồn]

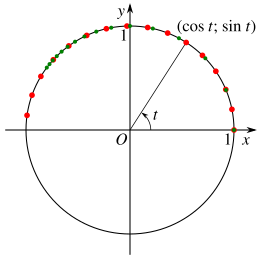
Biểu diễn tham số của đường tròn đơn vị:
Đỏ: $x=\cos t;\ y=\sin t$
Xanh: $x={\tfrac {1-\tau ^{2}}{1+\tau ^{2}}};\ y={\tfrac {2\tau }{1+\tau ^{2}}}$
Cả hai cách đều thỏa mãn phương trình đường tròn $x^{2}+y^{2}=1.$

Trong động học, quỹ đạo của vật trong không gian thường được miêu tả như là đường cong tham số hóa, với mỗi tọa độ không gian phụ thuộc tường minh vào một tham số độc lập (thường là thời gian). Sử dụng theo cách này, hệ phương trình tham số cho tọa độ của đối tượng làm thành hàm trị vectơ cho vị trí. Từ các đường cong tham số hóa này có thể thực hiện tích phân và vi phân theo tham số độc lập. Do đó, nếu vị trí của một hạt được miêu tả theo tham số

\mathbf {r} (t)=(x(t),y(t),z(t))

thì vận tốc của nó bằng

\mathbf {v} (t)=\mathbf {r} '(t)=(x'(t),y'(t),z'(t))

và gia tốc tìm được

\mathbf {a} (t)=\mathbf {r} ''(t)=(x''(t),y''(t),z''(t))

.

Thiết kế hỗ trợ bởi máy tính[sửa | sửa mã nguồn]

Một ứng dụng quan trọng khác của phương trình tham số đó là được áp dụng trong thiết kế hỗ trợ bởi máy tính (CAD).^[5] Ví dụ, xét ba biểu diễn sau đây của các đường cong phẳng.

Loại	Dạng	Ví dụ	Miêu tả
1. Tường minh	$y=f(x)\,\!$	$y=mx+b\,\!$	Đường thẳng
2. Hàm ẩn	$f(x,y)=0\,\!$	$\left(x-a\right)^{2}+\left(y-b\right)^{2}=r^{2}$	Đường tròn
3. Tham số	$x={\frac {g(t)}{w(t)}}$ ; $y={\frac {h(t)}{w(t)}}$	$x=a_{0}+a_{1}t;\,\!$ $y=b_{0}+b_{1}t\,\!$ $x=a+r\,\cos t;\,\!$ $y=b+r\,\sin t\,\!$	Đường thẳng Đường tròn

Hai loại đầu tiên được gọi là loại biểu diễn giải tích, hay không có tham số, của các đường cong; khi so sánh với cách biểu diễn tham số được ứng dụng trong các chương trình CAD, các cách biểu diễn giải tích có những nhược điểm của chúng. Đặc biệt, những cách biểu diễn không có tham số phụ thuộc vào lựa chọn hệ tọa độ và không thể hiện được hết tính chất của đối tượng qua các phép biến đổi hình học, như phép quay, tịnh tiến, và phóng to thu nhỏ; do vậy cách biểu diễn giải tích khiến cho khó phát sinh tạo điểm trên đường cong. Các vấn đề này có thể khắc phục được bằng cách viết các phương trình dưới dạng tham số.^[6]

Các hình có độ dài cạnh là số nguyên[sửa | sửa mã nguồn]

Nhiều bài toán trong tìm các hình có độ dài cạnh là số nguyên (tam giác nguyên) có thể đưa ra lời giải bằng phương trình tham số. Một ví dụ đó là tham số hóa Euclid của tam giác vuông sao cho độ dài các cạnh bên của nó $a, b$ và cạnh huyền $c$ là các số nguyên tố cùng nhau. Vì a và b không thể đồng thời là số chẵn (bằng không $a, b$ và $c$ không thể nguyên tố cùng nhau), ta có thể coi $a$ là số chẵn, và viết các cạnh dưới dạng tham số như sau

a=2mn,\ \ b=m^{2}-n^{2},\ \ c=m^{2}+n^{2},

trong đó các tham số $m$ và $n$ là những số nguyên dương nguyên tố cùng nhau và không đồng thời là số lẻ.

Bằng cách nhân $a, b$ và $c$ với một số nguyên dương bất kỳ, có thể thu được dạng tham số hóa của mọi tam giác vuông mà ba cạnh đều có độ dài là các số tự nhiên.

Xem thêm[sửa | sửa mã nguồn]

Tham khảo[sửa | sửa mã nguồn]

^ ^a ^b ^c Weisstein, Eric W. “Parametric Equations”. MathWorld.
^ Thomas, George B.; Finney, Ross L. (1979). Calculus and Analytic Geometry . Addison-Wesley. tr. 91.
^ Nykamp, Duane. “Plane parametrization example”. mathinsight.org. Truy cập ngày 14 tháng 4 năm 2017.
^ Spitzbart, Abraham (1975). Calculus with Analytic Geometry. Gleview, IL: Scott, Foresman and Company. ISBN 0-673-07907-4. Truy cập ngày 30 tháng 8 năm 2015.
^ Stewart, James (2003). Calculus (ấn bản 5). Belmont, CA: Thomson Learning, Inc. tr. 687–689. ISBN 0-534-39339-X.
^ Shah, Jami J.; Martti Mantyla (1995). Parametric and feature-based CAD/CAM: concepts, techniques, and applications. New York, NY: John Wiley & Sons, Inc. tr. 29–31. ISBN 0-471-00214-3.

Liên kết ngoài[sửa | sửa mã nguồn]

Weisstein, Eric W., "Parametric Equations" từ MathWorld.
Graphing Software trên DMOZ
Web application to draw parametric curves on the plane

[MathWorld-1] Weisstein, Eric W. “Parametric Equations”. MathWorld.

[2] Thomas, George B.; Finney, Ross L. (1979). Calculus and Analytic Geometry . Addison-Wesley. tr. 91.

[3] Nykamp, Duane. “Plane parametrization example”. mathinsight.org. Truy cập ngày 14 tháng 4 năm 2017.

[4] Spitzbart, Abraham (1975). Calculus with Analytic Geometry. Gleview, IL: Scott, Foresman and Company. ISBN 0-673-07907-4. Truy cập ngày 30 tháng 8 năm 2015.

[5] Stewart, James (2003). Calculus (ấn bản 5). Belmont, CA: Thomson Learning, Inc. tr. 687–689. ISBN 0-534-39339-X.

[6] Shah, Jami J.; Martti Mantyla (1995). Parametric and feature-based CAD/CAM: concepts, techniques, and applications. New York, NY: John Wiley & Sons, Inc. tr. 29–31. ISBN 0-471-00214-3.

[1]

[2]

[3]

[4]

[5]

[6]