Khác biệt giữa bản sửa đổi của “Siêu đồ thị”

Nội dung được xóa Nội dung được thêm vào

Nội tuyến

Phiên bản lúc 06:00, ngày 8 tháng 6 năm 2013

An example of a hypergraph, with $X=\{v_{1},v_{2},v_{3},v_{4},v_{5},v_{6},v_{7}\}$ and $E=\{e_{1},e_{2},e_{3},e_{4}\}=$ $\{\{v_{1},v_{2},v_{3}\},$ $\{v_{2},v_{3}\},$ $\{v_{3},v_{5},v_{6}\},$ $\{v_{4}\}\}$ .

Trong toán học,một siêu đồ thị là sự tổng quát của 1 đồ thị trong đó một cạnh có thể nối với bất kỳ đỉnh nào. Về mặt hình thức, một siêu đồ thị H là một cặp H=(E,X ) mà X là một tập hợp của các yếu tố được gọi là các nút hay đỉnh ,và E là một tập hợp các tập con khác rỗng của X gọi là siêu cạnh hoặc cạnh . Do đó, E là một tập hợp con của P(x) \ {0} , mà P(X) là power set của X. Trong khi cạnh đồ thị là các cặp nút ,siêu cạnh là bộ tùy ý của các nút. Do đó có thể chứa một số lượng tùy ý các nút. Tuy nhiên nó thường là mong muốn để nghiên cứu các siêu đồ thị, nơi mà tất cả siêu cạnh có cùng hướng, một siêu đồ thị – k cùng kiểu dữ liệu là một siêu đồ thị như là tất cả siêu cạnh của nó có kích thước k.

(Nói cách khác, nó là một sự kết hợp các bộ kích thước  k .)

Vì vậy , siêu đồ thị có 2 đồng dạng là một đồ thị. Siêu đồ thị có 3 đồng dạng cùng kiểu dữ liệu là sự kết hợp tập hợp tập bộ ba không có thứ tự,và tiếp tục như vậy.

Thuật ngữ

Do các liên kết của siêu đồ thị có thể có bất kỳ số các yếu tố trong một tập hợp, có một vài ký hiệu của các khái niệm về một đồ thị con, được gọi là siêu đồ thị con, siêu đồ thị bộ phận và siêu đồ thị phần.

Cho H = (X, E) là siêu đồ thị bao gồm đỉnh X = {xi | i Iv} và có tiến bộ: E = {ei | i  Ie, ei  X}

Nơi Iv và Ie là bộ chỉ số của các đỉnh và các cạnh tương ứng. Một siêu đồ thị con là một siêu đồ thị với một số đỉnh bị loại bỏ. Về mặt hình thức, các siêu đồ thị con HA sinh ra bởi một tập hợp con A của X được định nghĩa là. HA = (A,{ei  A | ei  A ≠ } ). Các phần siêu đồ thị là một siêu đồ thị với một số cạnh bị loại bỏ. Cho một tập hợp con J  Je tập hợp con của tập chỉ số cạnh, siêu đồ thị một phần được tạo ra bởi J là siêu đồ thị: (X,{ei | i  J}) Cho một tập hợp con A  X , siêu đồ thị được chọn là siêu đồ thị riêng phần: H x A = (A,{ei | i  Ie, ei  A}). Đối ngẫu H* của H là một siêu đồ thị mà các đỉnh và các cạnh được thay đổi cho nhau, vì vậy mà các đỉnh được cho bởi {ei} và có các cạnh được cho bởi {Xm}: Xm = {ei | x¬m  e¬¬i}.

Khi một khái niệm về phép bằng được xác định đúng, như thực hiện dưới đây, phép toán lấy đối ngẫu một siêu đồ thị là một phép nâng lên lũy thừa. (H*)* = H.

Một đồ thị kết nối G có tập đỉnh giống tập đỉnh của một siêu đồ thị kết nối H là một đồ thị chính của H nếu mỗi siêu đồ thị H sinh ra một đồ thị con được kết nối trong G. Đối với đồ thị không kết nối H, G là một đồ thị chính nếu có một song ánh giữa thành phần kết nối của G và H, sao cho mỗi kết nối thành phần G 'của G là một loạt các tương ứng với H'.

Một siêu đồ thị là song phương (hai bên) khi và chỉ khi các đỉnh của nó có thể được phân chia thành hai loại U và V mà mỗi siêu cạnh với số các yếu tố trong một tập hợp ít nhất 2 chứa tối thiểu một đỉnh từ cả hai lớp.

Đồ thị nguyên thủy của siêu đồ thị là đồ thị với đỉnh giống nhau của siêu đồ thị và các cạnh giữa các cặp đỉnh được chứa trong cùng một siêu cạnh. Đồ thị nguyên thủy đôi khi còn được gọi là đồ thị Gaifman.

Mô hình đồ thị song phương

Một siêu đồ thị H có thể là đại diện cho bởi một đồ thị song phương BG như sau: bộ X và E là phân vùng của BG Và ( x1, e1 ) được nối với cạnh nếu và chỉ nếu đỉnh x1 chứa trong cạnh e1 trong H. Ngược lại , đồ thị xong phương nào với bộ phận cố định và không có các nút không liên quan trong phần thứ hai đại diện cho một số siêu đồ thị theo cách mô tả ở trên , Đồ thị song phương này cũng được gọi là đồ thị tỷ lệ.

Tính không tuần hoàn

Tương phản với đồ thị vô hướng thường theo đó có một khái niệm tự nhiên của tuần hoàn và đồ thị không tuần hoàn ,có nhiều định nghĩa tương đương không tự nhiên của tính không tuần hoàn cho nhiều siêu đồ thị. Định nghĩa thứ nhất của tính không tuần hoàn cho nhiều siêu đồ thị được tính bằng cách lấy Claude Berge;một siêu đồ thị là không tuần hoàn Berge nếu nó là đồ thị liên thuộc(đồ thị song phương định nghĩa ở trên) là không tuần hoàn. nếu đồ thị nguyên thuỷ của nó là không tuần hoàn .Định nghĩa này là rất hạn chế : ví dụ,nếu siêu đồ thị có vài cặp v ≠ v’của các đỉnh và một vài cặp f ≠ f’ của các siêu đồ thị sao cho v,v’  f và v,v’  f’ thì nó là chu kỳ Berge. Chu kỳ Berge có thể một cách rõ ràng hiển nhiên là phép thử kiểm định trong thời gian tuyến tính bằng khám phá đồ thị liên thuộc. Chúng ta có thể định nghĩa khái niệm yếu của tính không tuần hoàn siêu đồ thị [ 4 ], chậm hơn số hạng tính không tuần hoàn α. Khái niệm này của tính không tuần hoàn tương đương với siêu đồ thị được bảo giác (mỗi đẳng phái của đồ thị nguyên thuỷ được che phủ bằng một vài siêu đồ thị) và đồ thị nguyên thuỷ của nó đang có hình sợi dây ; nó cũng tương đương đến tính khả quy đến đồ thị trống rỗng qua thuật toán GYO ( cũng gọi là thuật toán của Graham ). Trong lý thuyết lĩnh vực cơ sở dữ liệu, ta biết rằng lược đồ cơ sở dữ liệu thích một số tính chất hấp dẫn nếu siêu đồ thị bên dưới nó là không tuần hoàn α. Hơn nữa, tính không tuần hoàn α cũng là liên quan đến hàm ý của đoạn được che theo thứ tự lôgic. Chúng ta có thể phép thử kiểm định trong thời gian tuyến tính nếu siêu đồ thị là không tuần hoàn α Lưu ý là tính không tuần hoàn α có tính chất trái với mong đợi mà thêm các siêu cạnh vào siêu đồ thị có chu trình α có thể làm nó không tuần hoàn α ( chẳng hạn như, cộng vào siêu cạnh chứa toàn bộ các đỉnh của siêu đồ thị luôn luôn làm nó không tuần hoàn α). Thúc đẩy phần nào bằng khiếm khuyết đựơc nhìn nhận này, Ronald Fagin định nghĩa khái niệm mang tính không tuần hoàn β và tính không tuần hoàn γ. Chúng ta có thể phát biểu rằng tính không tuần hoàn β khi yêu cầu toàn bộ siêu đồ thị con của siêu đồ thị là không tuần hoàn α, là tương đương để định nghĩa trước đây bằng Graham. Khái niệm của tính không tuần hoàn γ là hạn chế hơn điều kiện mà tương đương với vài yêu cầu của lược đồ cơ sở dữ liệu và được liên quan đến đồ thị Bachman. Cả hai tính không tuần hoàn β và tính không tuần hoàn γ có thể kiểm định trong thời gian đa thức.

Chúng ta có thể phép thử kiểm định trong thời gian tuyến tính nếu siêu đồ thị là không tuần hoàn α .

Phép đẳng cấu và đẳng thức

Một đồng cấu Siêu đồ thị là một xạ ảnh từ tập đỉnh của một Siêu đồ thị khác như vậy mà mỗi cạnh của xạ ảnh tới một cạnh khác Một siêu đồ thị H = (X, E) là đẳng cấu với một siêu đồ thị G = (Y, F), được viết như H  Gif nếu tồn tại một song ánh  : X  Y và một hoán vị  của I như vậy mà (ei) = f(i) Các song ánh  sau đó được gọi là đẳng cấu của các đồ thị. lưu ý rằng H  G nếu và chỉ nếu H*  G* Khi các cạnh của một siêu đồ thị được dán nhãn rõ ràng, ta có một khái niệm bổ sung đẳng cấu mạnh. Ta nói rằng H là đẳng cấu mạnh với G nếu hoán vị là phân biệt. Sau đó người ta viết H  G. Lưu ý rằng tất cả các đồ thị đẳng cấu mạnh là đẳng cấu, nhưng không phải ngược lại. Khi các đỉnh của một siêu đồ thị được dán nhãn rõ ràng, chúng ta có các khái niệm về tính tương đương, và cũng về phép bằng. Ta nói rằng H là tương đương với G, và viết H  G nếu đẳng cấu  có (xn) = yn và (ei) = f(i) Ghi chú rằng: H  G nếu và chỉ nếu H*  G*

Ngoài ra, hoán vị  là đồng nhất, người ta nói rằng H bằng G, và viết H = G. Lưu ý rằng, với định nghĩa về tính tương đồng, đồ thị là tự đối ngẫu. (H*)* = H Một siêu đồ thị tự đẳng cấu là một đẳng cấu từ một tập đỉnh vào chính nó, đó là ghi nhãn lại các đỉnh. Tập hợp các tự đẳng cấu của một siêu đồ thị H (= (X, E)) là một nhóm thuộc thành phần, được gọi là nhóm tự đẳng cấu của siêu đồ thị và được viết thành Aut(H).

Ví dụ

Xem xét các siêu đồ thị H với các cạnh H = {e1 = {a,b}, e2 = {b,c}, e3 = {c,d}, e4 = {d,a}, e5 = {b,d}, e6 = {a,c}} và G = {f1 = {,}, f2 = {,}, f3 = {,}, f4 = {,}, f5 = {,}, f6 = {,}} Thì rõ ràng H và G là đẳng cấu (với (a) = , v.v…), nhưng chúng không phải là đẳng cấu mạnh. Vì vậy, ví dụ, trong H, đỉnh  đáp ứng các cạnh 1, 4 và 6, vì vậy: e1  e4  e¬6 = {a} Trong đồ thị G, không tồn tại bất kỳ đỉnh đáp ứng các cạnh 1, 4 và 6: f¬1  f4  f6 =  Trong ví dụ này, H và G là tương đương, H  G, và các đối ngẫu là đẳng cấu mạnh: H*  G*

Symmetric hypergraphs

The rank $r(H)$ of a hypergraph $H$ is the maximum cardinality of any of the edges in the hypergraph. If all edges have the same cardinality k, the hypergraph is said to be uniform or k-uniform, or is called a k-hypergraph. A graph is just a 2-uniform hypergraph.

The degree d(v) of a vertex v is the number of edges that contain it. H is k-regular if every vertex has degree k.

The dual of a uniform hypergraph is regular and vice-versa.

Two vertices x and y of H are called symmetric if there exists an automorphism such that $\phi (x)=y$ . Two edges $e_{i}$ and $e_{j}$ are said to be symmetric if there exists an automorphism such that $\phi (e_{i})=e_{j}$ .

A hypergraph is said to be vertex-transitive (or vertex-symmetric) if all of its vertices are symmetric. Similarly, a hypergraph is edge-transitive if all edges are symmetric. If a hypergraph is both edge- and vertex-symmetric, then the hypergraph is simply transitive.

Because of hypergraph duality, the study of edge-transitivity is identical to the study of vertex-transitivity.

Transversals

A transversal (or "hitting set") of a hypergraph H = (X, E) is a set $T\subseteq X$ that has nonempty intersection with every edge. A transversal T is called minimal if no proper subset of T is a transversal. The transversal hypergraph of H is the hypergraph (X, F) whose edge set F consists of all minimal transversals of H.

Computing the transversal hypergraph has applications in combinatorial optimization, in game theory, and in several fields of computer science such as machine learning, indexing of databases, the satisfiability problem, data mining, and computer program optimization.

Incidence matrix

Let $V=\{v_{1},v_{2},~\ldots ,~v_{n}\}$ and $E=\{e_{1},e_{2},~\ldots ~e_{m}\}$ . Every hypergraph has an $n\times m$ incidence matrix $A=(a_{ij})$ where

a_{ij}=\left\{{\begin{matrix}1&\mathrm {if} ~v_{i}\in e_{j}\\0&\mathrm {otherwise} .\end{matrix}}\right.

The transpose $A^{t}$ of the incidence matrix defines a hypergraph $H^{*}=(V^{*},\ E^{*})$ called the dual of $H$ , where $V^{*}$ is an m-element set and $E^{*}$ is an n-element set of subsets of $V^{*}$ . For $v_{j}^{*}\in V^{*}$ and $e_{i}^{*}\in E^{*},~v_{j}^{*}\in e_{i}^{*}$ if and only if $a_{ij}=1$ .

Hypergraph coloring

Hypergraph coloring is defined as follows. Let $H=(V,E)$ be a hypergraph such that $\Vert V\Vert =n$ . Then $C=\{c_{1},c_{2},\ldots ,c_{n}\}$ is a proper coloring of $H$ if and only if, for all $e\in E,\vert e\vert >1,$ there exists $v_{i},v_{j}\in e$ such that $c_{i}\neq c_{j}$ . In other words, there must be no monochromatic hyperedge with cardinality at least 2.

Hypergraphs for which there exists a coloring using up to k colors are referred to as k-colorable. The 2-colorable hypergraphs are exactly the bipartite ones.

Partitions

A partition theorem due to E. Dauber^[1] states that, for an edge-transitive hypergraph $H=(X,E)$ , there exists a partition

(X_{1},X_{2},\cdots ,X_{K})

of the vertex set $X$ such that the subhypergraph $H_{X_{k}}$ generated by $X_{k}$ is transitive for each $1\leq k\leq K$ , and such that

\sum _{k=1}^{K}r\left(H_{X_{k}}\right)=r(H)

where $r(H)$ is the rank of H.

As a corollary, an edge-transitive hypergraph that is not vertex-transitive is bicolorable.

Graph partitioning (and in particular, hypergraph partitioning) has many applications to IC design^[2] and parallel computing.^[3]^[4]^[5]

Theorems

Many theorems and concepts involving graphs also hold for hypergraphs. Ramsey's theorem and Line graph of a hypergraph are typical examples. Some methods for studying symmetries of graphs extend to hypergraphs.

Two prominent theorems are the Erdős–Ko–Rado theorem and the Kruskal–Katona theorem on uniform hypergraphs.

Hypergraph drawing

This circuit diagram can be interpreted as a drawing of a hypergraph in which four vertices (depicted as white rectangles and disks) are connected by three hyperedges drawn as trees.

Although hypergraphs are more difficult to draw on paper than graphs, several researchers have studied methods for the visualization of hypergraphs.

In one possible visual representation for hypergraphs, similar to the standard graph drawing style in which curves in the plane are used to depict graph edges, a hypergraph's vertices are depicted as points, disks, or boxes, and its hyperedges are depicted as trees that have the vertices as their leaves.^[6]^[7] If the vertices are represented as points, the hyperedges may also be shown as smooth curves that connect sets of points, or as simple closed curves that enclose sets of points.^[8]^[9]

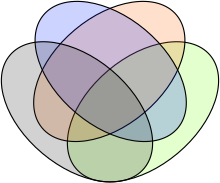
In another style of hypergraph visualization, the subdivision model of hypergraph drawing,^[10] the plane is subdivided into regions, each of which represents a single vertex of the hypergraph. The hyperedges of the hypergraph are represented by contiguous subsets of these regions, which may be indicated by coloring, by drawing outlines around them, or both. An order-n Venn diagram, for instance, may be viewed as a subdivision drawing of a hypergraph with n hyperedges (the curves defining the diagram) and 2ⁿ − 1 vertices (represented by the regions into which these curves subdivide the plane). In contrast with the polynomial-time recognition of planar graphs, it is NP-complete to determine whether a hypergraph has a planar subdivision drawing,^[11] but the existence of a drawing of this type may be tested efficiently when the adjacency pattern of the regions is constrained to be a path, cycle, or tree.^[12]

Generalizations

One possible generalization of a hypergraph is to allow edges to point at other edges. There are two variations of this generalization. In one, the edges consist not only of a set of vertices, but may also contain subsets of vertices, ad infinitum. Set membership then provides an ordering, but the ordering is neither a partial order nor a preorder, since it is not transitive. The graph corresponding to the Levi graph of this generalization is a directed acyclic graph. Consider, for example, the generalized hypergraph whose vertex set is $V=\{a,b\}$ and whose edges are $e_{1}=\{a,b\}$ and $e_{2}=\{a,e_{1}\}$ . Then, although $b\in e_{1}$ and $e_{1}\in e_{2}$ , it is not true that $b\in e_{2}$ . However, the transitive closure of set membership for such hypergraphs does induce a partial order, and "flattens" the hypergraph into a partially ordered set.

Alternately, edges can be allowed to point at other edges, (irrespective of the requirement that the edges be ordered as directed, acyclic graphs). This allows graphs with edge-loops, which need not contain vertices at all. For example, consider the generalized hypergraph consisting of two edges $e_{1}$ and $e_{2}$ , and zero vertices, so that $e_{1}=\{e_{2}\}$ and $e_{2}=\{e_{1}\}$ . As this loop is infinitely recursive, sets that are the edges violate the axiom of foundation. In particular, there is no transitive closure of set membership for such hypergraphs. Although such structures may seem strange at first, they can be readily understood by noting that the equivalent generalization of their Levi graph is no longer bipartite, but is rather just some general directed graph.

The generalized incidence matrix for such hypergraphs is, by definition, a square matrix, of a rank equal to the total number of vertices plus edges. Thus, for the above example, the incidence matrix is simply

\left[{\begin{matrix}0&1\\1&0\end{matrix}}\right].

Notes

^ E. Dauber, in Graph theory, ed. F. Harary, Addison Wesley, (1969) p. 172.
^ Karypis, G., Aggarwal, R., Kumar, V., and Shekhar, S. (1999), “Multilevel hypergraph partitioning: applications in VLSI domain”, IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 7 (1): 69–79, doi:10.1109/92.748202. Đã bỏ qua tham số không rõ |month= (trợ giúp)Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
^ Hendrickson, B., Kolda, T.G. (2000), “Graph partitioning models for parallel computing”, Parallel Computing, 26 (12): 1519–1545, doi:10.1016/S0167-8191(00)00048-X.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
^ Catalyurek, U.V. (1995). A Hypergraph Model for Mapping Repeated Sparse Matrix-Vector Product Computations onto Multicomputers. Đã bỏ qua tham số không rõ |coauthors= (gợi ý |author=) (trợ giúp); Đã bỏ qua tham số không rõ |booktitle= (trợ giúp)
^ Catalyurek, U.V. (1999), “Hypergraph-Partitioning Based Decomposition for Parallel Sparse-Matrix Vector Multiplication”, IEEE Transactions on Parallel and Distributed Systems, IEEE, 10 (7): 673–693, doi:10.1109/71.780863. Đã bỏ qua tham số không rõ |coauthors= (gợi ý |author=) (trợ giúp)
^ Sander, G. (2003), “Layout of directed hypergraphs with orthogonal hyperedges”, [[International Symposium on Graph Drawing|Proc. 11th International Symposium on Graph Drawing (GD 2003)]], Lecture Notes in Computer Science, 2912, Springer-Verlag, tr. 381–386 Tựa đề URL chứa liên kết wiki (trợ giúp).
^ Eschbach, Thomas; Günther, Wolfgang; Becker, Bernd (2006), “Orthogonal hypergraph drawing for improved visibility” (PDF), Journal of Graph Algorithms and Applications, 10 (2): 141–157.
^ Mäkinen, Erkki (1990), “How to draw a hypergraph”, International Journal of Computer Mathematics, 34 (3): 177–185, doi:10.1080/00207169008803875.
^ Bertault, François; Eades, Peter (2001), “Drawing hypergraphs in the subset standard”, Proc. 8th International Symposium on Graph Drawing (GD 2000), Lecture Notes in Computer Science, 1984, Springer-Verlag, tr. 45–76, doi:10.1007/3-540-44541-2_15.
^ Kaufmann, Michael; van Kreveld, Marc; Speckmann, Bettina (2009), “Subdivision drawings of hypergraphs”, Proc. 16th International Symposium on Graph Drawing (GD 2008), Lecture Notes in Computer Science, 5417, Springer-Verlag, tr. 396–407, doi:10.1007/978-3-642-00219-9_39.
^ Johnson, David S.; Pollak, H. O. (2006), “Hypergraph planarity and the complexity of drawing Venn diagrams”, Journal of graph theory, 11 (3): 309–325, doi:10.1002/jgt.3190110306.
^ Buchin, Kevin; van Kreveld, Marc; Meijer, Henk; Speckmann, Bettina; Verbeek, Kevin (2010), “On planar supports for hypergraphs”, Proc. 17th International Symposium on Graph Drawing (GD 2009), Lecture Notes in Computer Science, 5849, Springer-Verlag, tr. 345–356, doi:10.1007/978-3-642-11805-0_33.

References

Claude Berge, Dijen Ray-Chaudhuri, "Hypergraph Seminar, Ohio State University 1972", Lecture Notes in Mathematics 411 Springer-Verlag
Vitaly I. Voloshin. "Introduction to Graph and Hypergraph Theory". Nova Science Publishers, Inc., 2009.
Bài viết này có sử dụng tài liệu từ hypergraph tại PlanetMath, với giấy phép sử dụng Creative Commons Attribution/Share-Alike License.

[1] E. Dauber, in Graph theory, ed. F. Harary, Addison Wesley, (1969) p. 172.

[2] Karypis, G., Aggarwal, R., Kumar, V., and Shekhar, S. (1999), “Multilevel hypergraph partitioning: applications in VLSI domain”, IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 7 (1): 69–79, doi:10.1109/92.748202. Đã bỏ qua tham số không rõ |month= (trợ giúp)Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)

[3] Hendrickson, B., Kolda, T.G. (2000), “Graph partitioning models for parallel computing”, Parallel Computing, 26 (12): 1519–1545, doi:10.1016/S0167-8191(00)00048-X.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)

[4] Catalyurek, U.V. (1995). A Hypergraph Model for Mapping Repeated Sparse Matrix-Vector Product Computations onto Multicomputers. Đã bỏ qua tham số không rõ |coauthors= (gợi ý |author=) (trợ giúp); Đã bỏ qua tham số không rõ |booktitle= (trợ giúp)

[5] Catalyurek, U.V. (1999), “Hypergraph-Partitioning Based Decomposition for Parallel Sparse-Matrix Vector Multiplication”, IEEE Transactions on Parallel and Distributed Systems, IEEE, 10 (7): 673–693, doi:10.1109/71.780863. Đã bỏ qua tham số không rõ |coauthors= (gợi ý |author=) (trợ giúp)

[6] Sander, G. (2003), “Layout of directed hypergraphs with orthogonal hyperedges”, [[International Symposium on Graph Drawing|Proc. 11th International Symposium on Graph Drawing (GD 2003)]], Lecture Notes in Computer Science, 2912, Springer-Verlag, tr. 381–386 Tựa đề URL chứa liên kết wiki (trợ giúp).

[7] Eschbach, Thomas; Günther, Wolfgang; Becker, Bernd (2006), “Orthogonal hypergraph drawing for improved visibility” (PDF), Journal of Graph Algorithms and Applications, 10 (2): 141–157.

[8] Mäkinen, Erkki (1990), “How to draw a hypergraph”, International Journal of Computer Mathematics, 34 (3): 177–185, doi:10.1080/00207169008803875.

[9] Bertault, François; Eades, Peter (2001), “Drawing hypergraphs in the subset standard”, Proc. 8th International Symposium on Graph Drawing (GD 2000), Lecture Notes in Computer Science, 1984, Springer-Verlag, tr. 45–76, doi:10.1007/3-540-44541-2_15.

[10] Kaufmann, Michael; van Kreveld, Marc; Speckmann, Bettina (2009), “Subdivision drawings of hypergraphs”, Proc. 16th International Symposium on Graph Drawing (GD 2008), Lecture Notes in Computer Science, 5417, Springer-Verlag, tr. 396–407, doi:10.1007/978-3-642-00219-9_39.

[11] Johnson, David S.; Pollak, H. O. (2006), “Hypergraph planarity and the complexity of drawing Venn diagrams”, Journal of graph theory, 11 (3): 309–325, doi:10.1002/jgt.3190110306.

[12] Buchin, Kevin; van Kreveld, Marc; Meijer, Henk; Speckmann, Bettina; Verbeek, Kevin (2010), “On planar supports for hypergraphs”, Proc. 17th International Symposium on Graph Drawing (GD 2009), Lecture Notes in Computer Science, 5849, Springer-Verlag, tr. 345–356, doi:10.1007/978-3-642-11805-0_33.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]