Siêu đồ thị

Một ví dụ về siêu đồ thị, với $X=\{v_{1},v_{2},v_{3},v_{4},v_{5},v_{6},v_{7}\}$ và $E=\{e_{1},e_{2},e_{3},e_{4}\}=$ $\{\{v_{1},v_{2},v_{3}\},$ $\{v_{2},v_{3}\},$ $\{v_{3},v_{5},v_{6}\},$ $\{v_{4}\}\}$.

Trong toán học,một siêu đồ thị là sự tổng quát của 1 đồ thị trong đó một cạnh có thể nối với bất kỳ đỉnh nào. Về mặt hình thức, một siêu đồ thị $H$ là một cặp $H=(X,E)$ mà $X$ là một tập hợp của các yếu tố được gọi là các nút hay đỉnh,và $E$ là một tập hợp các tập con khác rỗng của $X$ gọi là siêu cạnh hoặc cạnh. Do đó,$E$ là một tập hợp con của ${\mathcal {P}}(X)\setminus \{\emptyset \}$, mà ${\mathcal {P}}(X)$ là power set của $X$

Trong khi cạnh đồ thị là các cặp nút,siêu cạnh là bộ tùy ý của các nút. Do đó có thể chứa một số lượng tùy ý các nút. Tuy nhiên nó thường là mong muốn để nghiên cứu các siêu đồ thị, nơi mà tất cả siêu cạnh có cùng hướng, một siêu đồ thị k cùng kiểu dữ liệu là một siêu đồ thị như là tất cả siêu cạnh của nó có kích thước k (Nói cách khác, nó là một sự kết hợp các bộ kích thước k). Vì vậy, siêu đồ thị có 2 đồng dạng là một đồ thị. Siêu đồ thị có 3 đồng dạng cùng kiểu dữ liệu là sự kết hợp tập hợp tập bộ ba không có thứ tự,và tiếp tục như vậy.

Thuật ngữ

Do các liên kết của siêu đồ thị có thể có bất kỳ số các yếu tố trong một tập hợp, có một vài ký hiệu của các khái niệm về một đồ thị con, được gọi là siêu đồ thị con, siêu đồ thị bộ phận và siêu đồ thị phần.

Cho $H=(X,E)$ là siêu đồ thị bao gồm đỉnh

$X=\lbrace x_{i}|i\in I_{v}\rbrace ,$

và có:

$E=\lbrace e_{i}|i\in I_{e},e_{i}\subseteq X\rbrace ,$

Nơi $I_{v}$ và $I_{e}$ là bộ chỉ số của các đỉnh và các cạnh tương ứng. Một siêu đồ thị con là một siêu đồ thị với một số đỉnh bị loại bỏ. Về mặt hình thức, các siêu đồ thị con $H_{A}$ sinh ra bởi một tập hợp con $A$ của $X$ được định nghĩa là.

$H_{A}=\left(A,\lbrace e_{i}\cap A|e_{i}\cap A\neq \varnothing \rbrace \right).$

Các phần siêu đồ thị là một siêu đồ thị với một số cạnh bị loại bỏ. Cho một tập hợp con $J\subset I_{e}$ tập hợp con của tập chỉ số cạnh, siêu đồ thị một phần được tạo ra bởi $J$ là siêu đồ thị:

$\left(X,\lbrace e_{i}|i\in J\rbrace \right).$

Cho một tập hợp con $A\subseteq X$, siêu đồ thị được chọn là siêu đồ thị bộ phận:

$H\times A=\left(A,\lbrace e_{i}|i\in I_{e},e_{i}\subseteq A\rbrace \right).$

Đối ngẫu $H^{*}$ của $H$ là một siêu đồ thị mà các đỉnh và các cạnh được thay đổi cho nhau, vì vậy mà các đỉnh được cho bởi $\lbrace e_{i}\rbrace$ và có các cạnh được cho bởi $\lbrace X_{m}\rbrace$:

$X_{m}=\lbrace e_{i}|x_{m}\in e_{i}\rbrace .$

Khi một khái niệm về phép bằng được xác định đúng, như thực hiện dưới đây, phép toán lấy đối ngẫu một siêu đồ thị là một phép nâng lên lũy thừa.

$\left(H^{*}\right)^{*}=H.$

Một đồ thị kết nối G có tập đỉnh giống tập đỉnh của một siêu đồ thị kết nối H là một đồ thị chính của H nếu mỗi siêu đồ thị H sinh ra một đồ thị con được kết nối trong G. Đối với đồ thị không kết nối H, G là một đồ thị chính nếu có một song ánh giữa thành phần kết nối của G và H, sao cho mỗi kết nối thành phần G 'của G là một loạt các tương ứng với H'.

Một siêu đồ thị là song phương (hai bên) khi và chỉ khi các đỉnh của nó có thể được phân chia thành hai loại U và V mà mỗi siêu cạnh với số các yếu tố trong một tập hợp ít nhất 2 chứa tối thiểu một đỉnh từ cả hai lớp.

Đồ thị nguyên thủy của siêu đồ thị là đồ thị với đỉnh giống nhau của siêu đồ thị và các cạnh giữa các cặp đỉnh được chứa trong cùng một siêu cạnh. Đồ thị nguyên thủy đôi khi còn được gọi là đồ thị Gaifman.

Mô hình đồ thị song phương

Một siêu đồ thị H có thể là đại diện cho bởi một đồ thị song phương BG như sau: bộ X và E là phân vùng của BG Và (x₁, e₁) được nối với cạnh nếu và chỉ nếu đỉnh x₁ chứa trong cạnh e₁ trong H. Ngược lại, đồ thị xong phương nào với bộ phận cố định và không có các nút không liên quan trong phần thứ hai đại diện cho một số siêu đồ thị theo cách mô tả ở trên. Đồ thị song phương này cũng được gọi là đồ thị tỷ lệ.

Tính không tuần hoàn

Tương phản với đồ thị vô hướng thường theo đó có một khái niệm tự nhiên của tuần hoàn và đồ thị không tuần hoàn,có nhiều định nghĩa tương đương không tự nhiên của tính không tuần hoàn cho nhiều siêu đồ thị. Định nghĩa thứ nhất của tính không tuần hoàn cho nhiều siêu đồ thị được tính bằng cách lấy Claude Berge;một siêu đồ thị là không tuần hoàn Berge nếu nó là đồ thị liên thuộc(đồ thị song phương định nghĩa ở trên) là không tuần hoàn. nếu đồ thị nguyên thủy của nó là không tuần hoàn.Định nghĩa này là rất hạn chế: ví dụ,nếu siêu đồ thị có vài cặp $v\neq v'$ của các đỉnh và một vài cặp $f\neq f'$ của các siêu đồ thị sao cho $v,v'\in f$ and $v,v'\in f'$ thì nó là chu kỳ Berge. Chu kỳ Berge có thể một cách rõ ràng hiển nhiên là phép thử kiểm định trong thời gian tuyến tính bằng khám phá đồ thị liên thuộc. Chúng ta có thể định nghĩa khái niệm yếu của tính không tuần hoàn siêu đồ thị, chậm hơn số hạng tính không tuần hoàn α. Khái niệm này của tính không tuần hoàn tương đương với siêu đồ thị được bảo giác (mỗi đẳng phái của đồ thị nguyên thủy được che phủ bằng một vài siêu đồ thị) và đồ thị nguyên thủy của nó đang có hình sợi dây; nó cũng tương đương đến tính khả quy đến đồ thị trống rỗng qua thuật toán GYO (cũng gọi là thuật toán của Graham). Trong lý thuyết lĩnh vực cơ sở dữ liệu, ta biết rằng lược đồ cơ sở dữ liệu thích một số tính chất hấp dẫn nếu siêu đồ thị bên dưới nó là không tuần hoàn α. Hơn nữa, tính không tuần hoàn α cũng là liên quan đến hàm ý của đoạn được che theo thứ tự lôgic. Chúng ta có thể phép thử kiểm định trong thời gian tuyến tính nếu siêu đồ thị là không tuần hoàn α Lưu ý là tính không tuần hoàn α có tính chất trái với mong đợi mà thêm các siêu cạnh vào siêu đồ thị có chu trình α có thể làm nó không tuần hoàn α (chẳng hạn như, cộng vào siêu cạnh chứa toàn bộ các đỉnh của siêu đồ thị luôn luôn làm nó không tuần hoàn α). Thúc đẩy phần nào bằng khiếm khuyết được nhìn nhận này, Ronald Fagin định nghĩa khái niệm mang tính không tuần hoàn β và tính không tuần hoàn γ. Chúng ta có thể phát biểu rằng tính không tuần hoàn β khi yêu cầu toàn bộ siêu đồ thị con của siêu đồ thị là không tuần hoàn α, là tương đương để định nghĩa trước đây bằng Graham. Khái niệm của tính không tuần hoàn γ là hạn chế hơn điều kiện mà tương đương với vài yêu cầu của lược đồ cơ sở dữ liệu và được liên quan đến đồ thị Bachman. Cả hai tính không tuần hoàn β và tính không tuần hoàn γ có thể kiểm định trong thời gian đa thức.

Chúng ta có thể phép thử kiểm định trong thời gian tuyến tính nếu siêu đồ thị là không tuần hoàn α.

Phép đẳng cấu và đẳng thức

Một đồng cấu Siêu đồ thị là một xạ ảnh từ tập đỉnh của một Siêu đồ thị khác như vậy mà mỗi cạnh của xạ ảnh tới một cạnh khác Một siêu đồ thị $H=(X,E)$ là đẳng cấu với một siêu đồ thị $G=(Y,F)$, được viết như $H\simeq G$ nếu tồn tại một song ánh

$\phi :X\to Y$

và một hoán vị $\pi$ của $I$ như vậy mà

$\phi (e_{i})=f_{\pi (i)}$

Các song ánh $\phi$ sau đó được gọi là đẳng cấu của các đồ thị. lưu ý rằng

$H\simeq G$ nếu và chỉ nếu $H^{*}\simeq G^{*}$.

Khi các cạnh của một siêu đồ thị được dán nhãn rõ ràng, ta có một khái niệm bổ sung đẳng cấu mạnh. Ta nói rằng $H$ là đẳng cấu mạnh với $G$ nếu hoán vị là phân biệt. Sau đó người ta viết $H\cong G$. Lưu ý rằng tất cả các đồ thị đẳng cấu mạnh là đẳng cấu, nhưng không phải ngược lại. Khi các đỉnh của một siêu đồ thị được dán nhãn rõ ràng, chúng ta có các khái niệm về tính tương đương, và cũng về phép bằng. Ta nói rằng $H$ là tương đương với $G$, và viết $H\equiv G$ nếu đẳng cấu $\phi$ có

$\phi (x_{n})=y_{n}$

và

$\phi (e_{i})=f_{\pi (i)}$

Ghi chú rằng:

$H\equiv G$ nếu và chỉ nếu $H^{*}\cong G^{*}$

Ngoài ra, hoán vị $\pi$ là đồng nhất, người ta nói rằng $H$ bằng$G$, và viết $H=G$. Lưu ý rằng, với định nghĩa về tính tương đồng, đồ thị là tự đối ngẫu.

$\left(H^{*}\right)^{*}=H$

Một siêu đồ thị tự đẳng cấu là một đẳng cấu từ một tập đỉnh vào chính nó, đó là ghi nhãn lại các đỉnh. Tập hợp các tự đẳng cấu của một siêu đồ thị H (= (X, E)) là một nhóm thuộc thành phần, được gọi là nhóm tự đẳng cấu của siêu đồ thị và được viết thành Aut(H).

Ví dụ

Xem xét các siêu đồ thị $H$ với các cạnh

$H=\lbrace e_{1}=\lbrace a,b\rbrace ,e_{2}=\lbrace b,c\rbrace ,e_{3}=\lbrace c,d\rbrace ,e_{4}=\lbrace d,a\rbrace ,e_{5}=\lbrace b,d\rbrace ,e_{6}=\lbrace a,c\rbrace \rbrace$

và

$G=\lbrace f_{1}=\lbrace \alpha ,\beta \rbrace ,f_{2}=\lbrace \beta ,\gamma \rbrace ,f_{3}=\lbrace \gamma ,\delta \rbrace ,f_{4}=\lbrace \delta ,\alpha \rbrace ,f_{5}=\lbrace \alpha ,\gamma \rbrace ,f_{6}=\lbrace \beta ,\delta \rbrace \rbrace$

Thì rõ ràng $H$ và $G$ là đẳng cấu (với $\phi (a)=\alpha$, v.v…), nhưng chúng không phải là đẳng cấu mạnh. Vì vậy, ví dụ, trong $H$, đỉnh $a$ đáp ứng các cạnh 1, 4 và 6, vì vậy:

$e_{1}\cap e_{4}\cap e_{6}=\lbrace a\rbrace$

Trong đồ thị $G$, không tồn tại bất kỳ đỉnh đáp ứng các cạnh 1, 4 và 6:

$f_{1}\cap f_{4}\cap f_{6}=\varnothing$

Trong ví dụ này, $H$ và $G$ là tương đương, $H\equiv G$, và các đối ngẫu là đẳng cấu mạnh: $H^{*}\cong G^{*}$.

Đồ thị đối xứng

Hạng $r(H)$ của siêu đồ thị $H$ là số lượng cực đại của bất cứ cạnh nào trong Siêu đồ thị. Nếu toàn bộ cạnh biên có cùng số lượng k, siêu đồ thị được cho là đồng dạng hay là đồng dạng k, hay là được gọi là Siêu đồ thị k. Đây chính xác là siêu đồ thị đồng dạng 2. Độ d(v) của đỉnh v là số cạnh chứa nó. Siêu đồ thị H gọi là k đều nếu mỗi đỉnh đều có độ k. Siêu đồ thị đối ngẫu là đều và ngược lại. Hai đỉnh x và y của siêu đồ thị H được gọi là đối xứng nếu ở H tồn tại tính tự đẳng cấu sao cho $\phi (x)=y$. Hai cạnh $e_{i}$ và $e_{j}$ được cho là đối xứng nếu ở đó tồn tại tính tự đẳng cấu sao cho $\phi (e_{i})=e_{j}$. Siêu đồ thị được cho là được bắc cầu đỉnh (hay là đối xứng đỉnh) nếu tất cả các đỉnh của nó là đối xứng. Nếu siêu đồ thị có cạnh song song và đối xứng đỉnh thì siêu đồ thị đó gọi là đối xứng đơn giản. Vì tính đối xứng của siêu đồ thị, tính chất bắc cầu của cạnh giống như tính chất bắc cầu ở các đỉnh.

Đường Hoành

Đường hoành của hypergraph H = (X, E) là tập hợp có $T\subseteq X$ giao với mỗi cạnh. Đường hoành T được gọi là cực tiểu nếu tập hợp con của nó cũng là một đường hoành. Siêu đồ thị đường hoành của H là siêu đồ thị (X, F) mà tập hợp cạnh F của nó gồm tất cả đường hoành cực tiểu của H. Tính toán siêu đồ thị đường hoành được ứng dụng trong tối ưu hoá tổ hợp, trí tuệ nhân tạo trong game và vài lĩnh vực khoa học máy tính như là máy học, chỉ số của cơ sở dữ liệu, bài toán thực nghiệm, khai thác dữ liệu, và tối ưu hoá chương trình tính.

Ma Trận Liên Thuộc

Cho $V=\{v_{1},v_{2},~\ldots ,~v_{n}\}$ và $E=\{e_{1},e_{2},~\ldots ~e_{m}\}$ mỗi siêu đồ thị có $n\times m$ ma trận liên thuộc $A=(a_{ij})$ trong đó: $a_{ij}=\left\{{\begin{matrix}1&\mathrm {if} ~v_{i}\in e_{j}\\0&\mathrm {otherwise} .\end{matrix}}\right.$. Chuyển vị $A^{t}$ của ma trận liên thuộc định nghĩa một siêu đồ thị $H^{*}=(V^{*},\ E^{*})$ gọi là đối ngẫu của H, $V^{*}$ là một tập hợp gồm m-phần tử và $E^{*}$ là một tập con gồm n phần tử của $V^{*}$. Ta có $v_{j}^{*}\in V^{*}$ và $e_{i}^{*}\in E^{*},~v_{j}^{*}\in e_{i}^{*}$ nếu và chỉ nếu $a_{ij}=1$.

Tô Màu Siêu Đồ Thị

Tô màu siêu đồ thị được định nghĩa như sau. Giả sử $H=(V,E)$ là siêu đồ thị sao cho $\Vert V\Vert =n$.Sau đó $C=\{c_{1},c_{2},\ldots ,c_{n}\}$ là màu chính của nếu $H$ và nếu chỉ nếu,tất cả $e\in E,\vert e\vert >1,$ ở đó tồn tại $v_{i},v_{j}\in e$ sao cho $c_{i}\neq c_{j}$. Nói cách khác, không thể có siêu cạnh đơn sắc với bản số lượng phần tử tối thiểu là 2. Các siêu đồ thị mà có tồn tại một cách tô màu sao cho sử dụng hết k màu được gọi là tô được k màu. Siêu đô thị tô được 2 màu chính là siêu đồ thị song phương.

Phân hoạch

Định lý phân hoạch của E. Dauber phát biểu như sau, cho cạnh biên - bắc cầu của Siêu đồ thị $H=(X,E)$, ở đó tồn tại phân hoạch:$(X_{1},X_{2},\cdots ,X_{K})$ của tập hợp đỉnh $X$ sao cho siêu đồ thị con $H_{X_{k}}$ tạo ra bởi $X_{k}$ là bắc cầu đối với mỗi $1\leq k\leq K$, và sao cho:$\sum _{k=1}^{K}r\left(H_{X_{k}}\right)=r(H)$ mà $r(H)$ là hạng của H. Hệ quả là, một siêu đồ thị có cạnh bắc cầu thì không phải là đỉnh bắc cầu tô được 2 màu. Phân hoạch đồ thị (nói riêng là phân hoạch siêu đồ thị) có ứng dụng trong thiết kế IC và tính toán song song.

Định lý

Nhiều định lý và khái niệm liên quan tới đồ thị vẫn được áp dụng cho siêu đồ thị. Một số phương pháp nghiên cứu tính đối xứng của các đồ thị được mở rộng cho siêu đồ thị. Hai định lý nổi tiếng là định lý Erdős–Ko–Rado và định lý Kruskal–Katona nói về siêu đồ thị đồng dạng.

Vẽ siêu đồ thị

Biểu đồ mạch này có thể được hiểu như là một hình vẽ của siêu đồ thị 4 đỉnh (hình chữ nhật và hình tròn màu trắng) được nối với nhau bởi 3 siêu cạnh tương tự như 3 cây.

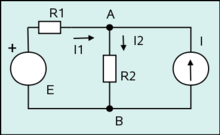
Mặc dù siêu đồ thị khó vẽ trên giấy hơn đồ thị thường nhưng các nhà nghiên cứu đã tìm ra phương pháp cho việc hình dung về nó. Một cách nhìn trực quan về siêu đồ thị, tương tự như cách vẽ của một đồ thị thường, các đường cong trong mặt phẳng dùng để vẽ các cạnh. Các đỉnh của siêu đồ thị được vẽ như các điểm, hình tròn hay hình chữ nhật và các siêu cạnh được vẽ như cây với lá là các đỉnh. Nếu đỉnh được vẽ như các điểm, thì siêu cạnh có thể được biểu diễn như những đường cong nối với các điểm đó, hoặc những đường cong khép kín chứa tập hợp các điểm.

Một biểu đồ Venn 4 phần tử, thể hiện cho một siêu đồ thị với 15 đỉnh (15 vùng màu khác nhau) và 4 siêu cạnh (4 elip).

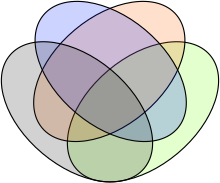
Một cách nhìn khác về siêu đồ thị, chia nhỏ khuôn mẫu của siêu đồ thị, chia mặt phẳng thành các vùng, mỗi vùng là một siêu cạnh, có thể được đánh dấu bằng màu sắc, đường viền xung quanh hoặc cả hai. Các đỉnh thì được mô tả như phần giao nhau của các vùng. Một biểu đồ Venn tập n là một điển hình, có thể được xem như một phần nhỏ của bức tranh về siêu đồ thị với n siêu cạnh (biểu diễn bởi các hình cong) và 2ⁿ − 1 đỉnh (biểu diễn bởi các vùng được sinh ra do những hình cong cắt nhau).

Tổng quát

Nhìn chung, siêu đồ thị cho phép các cạnh có thể nối với nhau. Có hai cách nhìn về vấn đề này. Một là các cạnh không chỉ bao gồm tập hợp các đỉnh mà còn có thể chứa tập con các đỉnh. Mỗi phần tử trong tập hợp tuân theo một thứ tự, nhưng thứ tự này không phải partial order mà cũng không phải preorder, vì nó không bắc cầu. Đồ thị đúng với đồ thị Levi trong cách nhìn này là đồ thị có hướng và không có chu trình. Xét ví dụ sau, một siêu đồ thị có tập đỉnh là $V=\{a,b\}$ và các cạnh $e_{1}=\{a,b\}$ và $e_{2}=\{a,e_{1}\}$. Mặc dù $b\in e_{1}$ và $e_{1}\in e_{2}$ nhưng $b\in e_{2}$ thì không đúng. Tuy nhiên, tính chất bao đóng bắc cầu của các phần tử trong tập hợp của siêu đồ thị đó lại tạo nên thứ tự riêng phần (partial order) và chia siêu đồ thị thành một tập hợp có thứ tự riêng phần. Lần lượt, một cạnh có thể được nối với cạnh khác, (Bất kể các cạnh có trật tự theo hướng, đồ thị không chu trình). Điều này cho phép độ thị có cạnh lặp, không cần phải chứa tất cả các đỉnh. Ví dụ, xét một siêu đồ thị gồm hai cạnh $e_{1}$ và $e_{2}$, không có đỉnh, vì thế $e_{1}=\{e_{2}\}$ và $e_{2}=\{e_{1}\}$. Dẫn đến việc lặp đệ quy vô tận, những tập hợp mà các cạnh vi phạm axiom of foundation. Cụ thể là không có tính chất bao đóng bắc cầu cho các phần tử trong tập hợp thuộc siêu đồ thị. Mặc dù những cấu trúc này có thể trông khác với cái đầu tiên nhưng chúng có thể được hiểu một cách dễ dàng bởi việc tổng quát hóa tương đương đồ thị Levi của chúng không còn phân đôi nữa, nhưng lại đúng hơn một số đồ thị có hướng. Ma trận liên thuộc của siêu đồ thị này là ma trận vuông, có hạng bằng tổng số đỉnh và cạnh. Vậy, trong ví dụ trên, ma trận liên thuộc chỉ đơn giản là:

$\left[{\begin{matrix}0&1\\1&0\end{matrix}}\right].$

Ứng dụng của siêu đồ thị

Cơ sở dữ liệu quan hệ

Trong những năm qua một số lượng đáng kể các nhà nghiên cứu đã dành thời gian và công sức để nghiên cứu, phân tích các quan hệ cơ sở dữ liệu – bằng phương pháp sử dụng các kỹ thuật liên quan đến đồ thị. Một quan hệ cơ sở dữ liệu (RDB) thường được thể hiện bằng một tập hợp các mối quan hệ trong một miền giá trị nào đó, cùng với tập hợp các Functional Dependencies Functional Dependencies đã được nghiên cứu bằng cách dùng loại đồ thị tổng quát chẳng hạn như FD – Graphs, Implication Graphs, Deduction Graphs Hay NBE có các tập thuộc tính của RDB, một sự phụ thuộc vào chức năng F(X,Y) với cả hai X và Y, đó là tập hợp con của N. Định nghĩa duy nhất của các giá trị thuộc tính Y khi giá trị X được đưa ra. Functional Dependencies có một số quy tắc cho phép chúng ta lấy thong tin mới đó lưu trữ một cách rõ ràng trong cơ sở dữ liệu. i. Reflexivity: ii. Transitivity: if and iii. Conjunction: F(X, Y) if F(X, Y), F(X, Z) Đấy là một tập hợp của Functional Dependencies, F, chúng ta có thể cần phải giải quyết các vấn đề như: • Tìm xem một Functional Dependencies cho F (X, Y) có thể xuất phát từ F và dựa trên kết luận của quy định. • Cho một tập hợp các thuộc tính X, ta phải tìm kiếm điểm kết thúc của nó so với F, tức là tìm thấy một thiết lập X*, như vậy rằng F(X, X*) thuộc về F

	Có một số nghiên cứu về hypergraphs như cung cấp các hình thức tự nhiên và thống nhất để đối phó với hầu hết các vấn đề phát sinh trong công việc phân tích Functional Dependencies trong RDB

Một tập hợp F của FD trên các thuộc tính thiết lập tồn tại, có thể được đại diện bởi một Hypergraph H = (V,E) với V = N và E = {(X, Y)\X; F(X,Y F, Y }. Nó rất là dễ dàng để thấy rằng một B là một con đường trên H, nó tương đương với một chuỗi các tác động dựa trên nguyên tắc (°). Ví dụ B – con đường của hình bên dưới tương ứng

Với gốc F{ 1, 2, 3, 4 }, {9, 10} bắt đầu từ mối quan hệ ý nghĩa.

Thủ tục B- Visit giải quyết những vấn đề (a) và (b) trong O (size(H)) = O(size(F)) ở một khoảng thời gian. Trong cả hai trường hợp tập Q được sử dụng trong B – visit được khởi tạo bởi X. Cho X’ là một tập hợp được ghé thăm bởi Đỉnh B – kết nối tới X. Trong vấn đề (a) câu trả lời là một tập hợp sinh ra bởi F(X, Y) sinh ra F chỉ khi Y khi và chỉ khi Y X’ trong khi vấn đề kia là (b) khi X = X’

Urban transit application (ứng dụng di chuyển trong thành phố)

Phân tích quá trình đi lại, vận chuyển hành khách trong một thành phố luôn là một ứng dụng thú vị với mô hình siêu đồ thị. Ở đây, hệ thống giao thông được miêu tả như một mô hình hóa mạng lưới đặc biệt, trong đó những đường vận chuyển được chồng lên hệ thống mặt đất. Mỗi dòng chuyển là một mạch, tức là một trình tự xen kẽ các node đại diện cho các dòng và vòng cung của một đại diện trong đoạn đường đi đó. Hệ thông đường đi dưới mặt đất được hình thành bởi các nút thể hiện ở vị trí địa lý (ở trọng tâm của một khu vực) trong một khu đô thị và vòng cung của đó đại diện cho con đường dành để đi bộ đến được trung tâm. Đổi với mỗi node I đang dừng trên mạng cơ sở, cho Li là một tập hợp các đường đi sẽ dừng lại ở I. Với mỗi node tôi sẽ được kết nối với các node tương ứng thuộc đường Li bởi một vòng cung để lại và một vòng cung ngược lên phía trên cao. Ta có hình minh họa sau đây Từ một quan điểm của cá nhân địa phương có tuyến đường đi đó thì, người nào đó ở những trạm dừng chân I đi đến những nơi mà họ muốn đến phải ít tốn kém về mặt thời gian và chi phí. Vấn đề được đặt ra trong các tập con của công thức sau, tập trên được gọi là một tập hấp dẫn – đúng đắn bởi vì nó luôn luôn lên những chuyến xe đầu tiên đi đến các trạm dừng chân, thời gian di chuyển dự kiến sẽ được giảm đi rất là nhiều. Nhìn chung, thời gian di chuyển trên chuyến xe và thời gian chờ để đi tiếp quảng đường khác, nó sẽ xảy ra trong những nhà chờ xe như vậy. Chuyến đi sẽ được bắt đầu nếu hành khác đó bỏ tiền ra và leo lên xe ngồi.