Tìm kiếm nhị phân

Bài này viết về tìm kiếm trên một mảng hữu hạn đã được sắp xếp. Đối với tìm kiếm các giá trị của một hàm liên tục, xem phương pháp chia đôi.

Tìm kiếm nhị phân

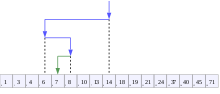Minh họa thuật toán tìm kiếm nhị phân, trong đó 7 là giá trị cần tìm
Phân loại	Thuật toán tìm kiếm
Cấu trúc dữ liệu	Mảng
Hiệu suất trường hợp tệ nhất	O(log n)
Hiệu suất trường hợp tốt nhất	O(1)
Hiệu suất trung bình	O(log n)
Độ phức tạp không gian trường hợp tệ nhất	O(1)
Tối ưu	Có

Trong khoa học máy tính, tìm kiếm nhị phân (tiếng Anh: binary search), còn gọi là tìm kiếm nửa khoảng (half-interval search), tìm kiếm logarit (logarithmic search), hay binary chop, là một thuật toán tìm kiếm xác định vị trí của một giá trị cần tìm trong một mảng đã được sắp xếp. Thuật toán tiến hành so sánh giá trị cần tìm với phần tử đứng giữa mảng. Nếu hai giá trị không bằng nhau, phần nửa mảng không chứa giá trị cần tìm sẽ bị bỏ qua và tiếp tục tìm kiếm trên nửa còn lại, một lần nữa lấy phần tử ở giữa và so sánh với giá trị cần tìm, cứ thế lặp lại cho đến khi tìm thấy giá trị đó. Nếu phép tìm kiếm kết thúc khi nửa còn lại trống thì giá trị cần tìm không có trong mảng.

Tìm kiếm nhị phân chạy theo thời gian logarit trong trường hợp tệ nhất, thực hiện $O(\log n)$ bước so sánh, trong đó $n$ là số phần tử trong mảng, $O$ là kí hiệu O lớn, và $\log$ là phép toán logarit. Thuật toán tìm kiếm nhị phân nhanh hơn so với tìm kiếm tuyến tính, ngoại trừ các trường hợp mảng có kích thước nhỏ. Tuy nhiên, mảng phải được sắp xếp trước khi áp dụng tìm kiếm nhị phân. Một số cấu trúc dữ liệu chuyên dụng được thiết kế cho việc tìm kiếm nhanh, ví dụ như bảng băm, có thể thực hiện tìm hiệu quả hơn tìm kiếm nhị phân. Tuy nhiên, thuật toán này có thể dùng để giải quyết nhiều loại vấn đề hơn, như tìm phần tử nhỏ nhất hoặc lớn nhất tiếp theo trong mảng so với giá trị cho trước, kể cả khi nó không có trong mảng.

Có nhiều biến thể của phép tìm kiếm nhị phân. Cụ thể, phương pháp "đổ xuống một phần" (fractional cascading) giúp tăng tốc tìm kiếm nhị phân với cùng một giá trị trong nhiều mảng. Phương pháp này cho phép giải quyết hiệu quả một số vấn đề về tìm kiếm trong hình học tính toán và nhiều lĩnh vực khác. Thuật toán tìm kiếm mũ (exponential search) mở rộng tìm kiếm nhị phân sang các danh sách không có giới hạn. Các cấu trúc dữ liệu cây tìm kiếm nhị phân và B-cây được xây dựng dựa trên tìm kiếm nhị phân.

Thuật toán

Thuật toán tìm kiếm nhị phân hoạt động trên các mảng đã được sắp xếp. Thuật toán bắt đầu bằng việc so sánh một phần tử đứng chính giữa mảng với giá trị cần tìm. Nếu bằng nhau, vị trí của nó trong mảng sẽ được trả về. Nếu giá trị cần tìm nhỏ hơn phần tử này, quá trình tìm kiếm tiếp tục ở nửa nhỏ hơn của mảng. Nếu giá trị cần tìm lớn hơn phần tử ở giữa, quá trình tìm kiếm tiếp tục ở nửa lớn hơn của mảng. Bằng cách này, ở mỗi phép lặp thuật toán có thể loại bỏ nửa mảng mà giá trị cần tìm chắc chắn không xuất hiện.

Quy trình

Cho một mảng $A$ có $n$ phần tử với các giá trị hoặc bản ghi $A_{0},A_{1},A_{2},\ldots ,A_{n-1}$đã được sắp xếp sao cho $A_{0}\leq A_{1}\leq A_{2}\leq \cdots \leq A_{n-1}$, và giá trị cần tìm $T$, chương trình con sau đây sử dụng tìm kiếm nhị phân để tìm chỉ số của $T$ trong $A$.

1. Gán $L$ với giá trị $0$ và $R$ với giá trị $n-1$.
2. Nếu $L>R$, tìm kiếm kết thúc (không thành công).
3. Gán $m$ (vị trí của phần tử đứng giữa) với giá trị floor của ${\frac {L+R}{2}}$, tức là số nguyên lớn nhất nhỏ hơn hoặc bằng ${\frac {L+R}{2}}$.
4. Nếu $A_{m}<T$, gán $L$ với $m+1$ và quay lại bước 2.
5. Nếu $A_{m}>T$, gán $R$ với $m-1$ và quay lại bước 2.
6. Khi $A_{m}=T$, quá trình tìm kiếm hoàn tất; trả về $m$.

Quy trình lặp này dùng hai biến $L$ và $R$ để lưu giới hạn tìm kiếm. Quy trình này có thể diễn giải bằng mã giả như dưới đây, trong đó tên các biến và kiểu giữ nguyên so với như trên, floor là hàm floor, và không_thành_công là một giá trị cụ thể thông báo tìm kiếm thất bại.

function binary_search(A, n, T) is
    L := 0
    R := n − 1
    while L ≤ R do
        m := floor((L + R) / 2)
        if A[m] < T then
            L := m + 1
        else if A[m] > T then
            R := m - 1
        else:
            return m
    return không_thành_công

Ngoài ra, thuật toán có thể lấy giá trị ceiling của ${\frac {L+R}{2}}$. Điều này có thể thay đổi kết quả nếu giá trị cần tìm xuất hiện nhiều hơn một lần trong mảng.

Cách làm khác

Trong quy trình trên, thuật toán kiểm tra phần tử ở giữa ($m$) có bằng giá trị cần tìm ($T$) không ở mỗi phép lặp. Một số cách làm bỏ qua bước này ở mỗi phép lặp. Khi đó thuật toán chỉ kiểm tra điều này khi chỉ còn một phần tử còn lại (khi $L=R$). Nhờ đó mà vòng lặp so sánh được thực hiện nhanh hơn do mỗi phép lặp đã loại bỏ được một bước so sánh. Tuy nhiên, với cách làm này thì số phép lặp trung bình tăng lên.

Hermann Bottenbruch cho xuất bản cách áp dụng đầu tiên bỏ qua bước kiểm tra này vào năm 1962.

1. Gán $L$ với giá trị $0$ và $R$ với giá trị $n-1$.
2. Khi $L\neq R$,
   1. Gán $m$ (vị trí của phần tử đứng giữa) với giá trị ceiling của ${\frac {L+R}{2}}$, tức là số nguyên nhỏ nhất lớn hơn hoặc bằng ${\frac {L+R}{2}}$.
   2. Nếu $A_{m}>T$, gán $R$ với $m-1$.
   3. Trường hợp còn lại, $A_{m}\leq T$; gán $L$ với $m$.
3. Khi $L=R$, quá trình tìm kiếm hoàn tất. Nếu $A_{L}=T$, trả về $L$. Nếu không, tìm kiếm thất bại.

Với ceil là hàm ceiling, mã giả cho phiên bản này như sau:

function binary_search_alternative(A, n, T) is
    L := 0
    R := n − 1
    while L != R do
        m := ceil((L + R) / 2)
        if A[m] > T then
            R := m - 1
        else:
            L := m
    if A[L] = T then
        return L
    return không_thành_công
    

Phần tử lặp lại

Quy trình trên có thể trả về bất cứ chỉ số nào có giá trị phần tử bằng giá trị cần tìm, kể cả khi trong mảng có các phần tử xuất hiện lặp lại. Ví dụ, với mảng $[1,2,3,4,4,5,6,7]$ và giá trị cần tìm là $4$, thuật toán có thể trả về một trong hai kết quả đúng là phần tử thứ 4 (chỉ số là 3) hoặc thứ 5 (chỉ số là 4). Quy trình chuẩn trong trường hợp này sẽ trả về phần tử thứ 4 (chỉ số 3). Thuật toán này không phải lúc nào cũng trả về vị trí đầu tiên xuất hiện giá trị cần tìm (ví dụ với mảng $[1,2,4,4,4,5,6,7]$, kết quả trả về vẫn là phần tử thứ 4). Tuy nhiên, có một số trường hợp cần phải tìm phần tử nằm xa nhất về phía bên trái hoặc bên phải mang giá trị cần tìm khi giá trị này xuất hiện lặp lại trong mảng. Trong ví dụ trên, phần tử thứ 4 là phần tử đứng xa nhất về bên trái mang giá trị 4, trong khi phần tử thứ 5 là phần từ đứng xa nhất về bên phải mang giá trị 4. Cách làm thứ hai ở trên sẽ luôn trả về chỉ số của phần tử đứng xa nhất về bên phải nếu tồn tại các phần tử lặp lại.

Quy trình tìm phần tử xa nhất về bên trái

Để tìm phần tử xa nhất về bên trái, ta có thể dùng quy trình sau:

1. Gán $L$ với giá trị $0$ và $R$ với $n$.
2. Khi $L<R$,
3. Gán $m$ (vị trí của phần tử đứng giữa) với giá trị floor của ${\frac {L+R}{2}}$, tức là số nguyên lớn nhất nhỏ hơn hoặc bằng ${\frac {L+R}{2}}$.
   1. Nếu $A_{m}<T$, gán $L$ với $m+1$.
   2. Trường hợp còn lại, $A_{m}\geq T$; gán $R$ với $m$.
4. Trả về $L$.

Nếu $L<n$ và $A_{L}=T$ thì $A_{L}$ là phần tử đứng xa nhất về bên trái có giá trị bằng $T$. Kể cả khi $T$ không nằm trong mảng, $L$ là hạng của $T$ trong mảng, hay số phần tử trong mảng nhỏ hơn $T$.

Với floor là hàm floor, mã giả cho phiên bản này như sau:

function binary_search_leftmost(A, n, T):
    L := 0
    R := n
    while L < R:
        m := floor((L + R) / 2)
        if A[m] < T:
            L := m + 1
        else:
            R := m
    return L

Quy trình tìm phần tử xa nhất về bên phải

Để tìm phần tử xa nhất về bên phải, ta có thể dùng quy trình sau:

1. Gán $L$ với giá trị $0$ và $R$ với $n$.
2. Khi $L<R$,
3. Gán $m$ (vị trí của phần tử đứng giữa) với giá trị floor của ${\frac {L+R}{2}}$, tức là số nguyên lớn nhất nhỏ hơn hoặc bằng ${\frac {L+R}{2}}$.
   1. Nếu $A_{m}>T$, gán $R$ với $m$.
   2. Trường hợp còn lại, $A_{m}\leq T$; gán $L$ với $m+1$.
4. Trả về $R-1$.

Nếu $L>0$ và $A_{L-1}=T$, thì $A_{L-1}$ là phần tử đứng xa nhất về phía bên phải có giá trị bằng $T$. Kể cả khi $T$ không có trong mảng, $n-L$ sẽ là số phần tử trong mảng lớn hơn $T$.

Với floor là hàm floor, mã giả cho phiên bản này như sau:

function binary_search_rightmost(A, n, T):
    L := 0
    R := n
    while L < R:
        m := floor((L + R) / 2)
        if A[m] > T:
            R := m
        else:
            L := m + 1
    return R - 1

Hiệu suất

Một cây biểu diễn tìm kiếm nhị phân. Mảng được dùng trong ví dụ này là $[20,30,40,50,80,90,100]$ và giá trị cần tìm là $40$.

Trường hợp tệ nhất là khi quá trình tìm kiếm phải đi tới bậc sâu nhất của cây, còn trường hợp tốt nhất là khi giá trị cần tìm chính là phần tử đứng giữa.

Về mặt số phép so sánh, hiệu suất của thuật toán tìm kiếm nhị phân có thể được phân tích bằng cách biểu diễn quá trình chạy thuật toán trên cây nhị phân. Nút gốc của cây là phần tử đứng giữa mảng. Phần tử đứng giữa nửa nhỏ hơn là nút con bên trái của nút gốc, và phần tử đứng giữa nửa lớn hơn là nút con bên phải của nút gốc. Phần còn lại của cây cũng được dựng như vậy. Bắt đầu từ nút gốc, tùy theo giá trị cần tìm nhỏ hơn hay lớn hơn nút đang xét mà thuật toán sẽ duyệt theo cây con bên trái hay bên phải.

Trong trường hợp tệ nhất, thuật toán thực hiện ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$ lần lặp so sánh, trong đó ${\textstyle \lfloor \rfloor }$ là ký hiệu của hàm floor cho kết quả là số nguyên lớn nhất nhỏ hơn hoặc bằng giá trị bên trong, và ${\textstyle \log _{2}}$ là phép logarit nhị phân. Nguyên nhân là do khi gặp phải trường hợp tệ nhất, thuật toán phải đi tới bậc sâu nhất trong cây, và số bậc trong cây luôn bằng ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$ với bất cứ phép tìm kiếm nhị phân nào.

Trường hợp tệ nhất còn có thể xảy ra khi giá trị cần tìm không có trong mảng. Nếu ${\textstyle n}$ ở dạng ${\textstyle 2^{\alpha }-1}$ thì trường hợp này luôn xảy ra. Nếu không, thuật toán có thể thực hiện ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$phép lặp nếu phải đi tới bậc sâu nhất của cây. Tuy nhiên, nếu thuật toán kết thúc ngay ở bậc sâu thứ hai của cây, quá trình tìm kiếm có thể chỉ cần thực hiện ${\textstyle \lfloor \log _{2}(n)\rfloor }$ phép lặp, ít hơn trường hợp tệ nhất một phép.

Giả sử mỗi phần tử có xác suất được thực hiện tìm kiếm như nhau, trung bình thuật toán tìm kiếm nhị phân thực hiện $\lfloor \log _{2}(n)\rfloor +1-(2^{\lfloor \log _{2}(n)\rfloor +1}-\lfloor \log _{2}(n)\rfloor -2)/n$ phép lặp khi phần tử cần tìm có mặt trong mảng, hay xấp xỉ bằng $\log _{2}(n)-1$. Khi phần tử cần tìm không có trong mảng, thuật toán thực hiện trung bình $\lfloor \log _{2}(n)\rfloor +2-2^{\lfloor \log _{2}(n)\rfloor +1}/(n+1)$ phép lặp, nếu giả sử khoảng giữa và bên ngoài các phần tử đều có xác suất được tìm như nhau.

Trong trường hợp tốt nhất, khi giá trị cần tìm nằm ngay giữa mảng, vị trí của nó được trả về ngay sau một phép lặp.

Về mặt số phép lặp, không có thuật toán tìm kiếm nào chỉ bằng so sánh các phần tử có thể có hiệu suất trung bình hay thậm chí trong trường hợp tệ nhất tốt hơn tìm kiếm nhị phân. Cây so sánh biểu diễn tìm kiếm nhị phân có số bậc ít nhất có thể do mọi bậc phía trên bậc thấp nhất của cây đều được lấp đầy hoàn toàn. Nếu không, thuật toán tìm kiếm có thể loại bỏ một vài phần tử trong mỗi phép lặp, làm tăng số phép lặp cần thực hiện trong trường hợp trung bình và tệ nhất. Các thuật toán tìm kiếm khác dùng cách so sánh đều bị rơi vào trường hợp này, do mặc dù chúng có thể chạy nhanh hơn với một số giá trị cần tìm nhất định, hiệu suất trung bình trên tất cả phần tử vẫn kém hơn tìm kiếm nhị phân. Bằng cách chia mảng thành hai nửa, thuật toán tìm kiếm nhị phân đảm bảo được kích thước của hai mảng con giống nhau nhất có thể.

Độ phức tạp không gian

Thuật toán tìm kiếm nhị phân cần ba con trỏ để trỏ tới các phần tử, bất kể kích thước của mảng; đó có thể là chỉ số các phần tử trong mảng hoặc con trỏ tới địa chỉ trong bộ nhớ. Tuy nhiên, thuật toán cần ít nhất $\left\lceil \log _{2}(n)\right\rceil$ bit để mã hóa một con trỏ tới một phần tử trong mảng có $n$ phần tử. Do đó, độ phức tạp không gian của tìm kiếm nhị phân là $O(\log n)$. Ngoài ra, thuật toán còn cần $O(n)$ không gian để lưu trữ mảng.

Trường hợp trung bình

Số phép lặp trung bình được thực hiện bởi thuật toán tùy thuộc vào xác suất mỗi phần tử được thực hiện tìm kiếm. Trường hợp trung bình khi tìm kiếm thành công và không thành công là khác nhau. Ta giả sử mỗi phần tử có xác suất được tìm như nhau nếu tìm kiếm thành công. Nếu tìm kiếm không thành công, ta giả sử các khoảng giữa và ngoài các phần tử có xác suất được tìm giống nhau. Trường hợp trung bình khi tìm kiếm thành công là số phép lặp cần thực hiện để tìm mọi phần tử chính xác một lần, chia cho $n$, số phần tử trong mảng. Trường hợp trung bình khi tìm kiếm không thành công là số phép lặp cần thực hiện để tìm một phần tử trong mọi khoảng chính xác một lần, chia cho $n+1$ khoảng.

Tìm kiếm thành công

Khi biểu diễn bằng cây nhị phân, một lần tìm kiếm thành công có thể được biểu diễn bằng một đường đi từ gốc tới nút cần tìm, gọi là đường đi trong (internal path). Độ dài của một đường đi là số cạnh (đường nối giữa các nút) mà đường đó đi qua. Số phép lặp mà một lần tìm kiếm thực hiện, với điều kiện độ dài của đường đi tương ứng với lần tìm đó là $l$, là $l+1$ tính cả phép lặp ban đầu. Độ dài đường đi trong (internal path length) là tổng độ dài tất cả các đường đi trong. Do chỉ có một đường đi duy nhất từ gốc tới bất cứ nút nào, mỗi đường trong đó biểu diễn cho một phép tìm kiếm phần tử tương ứng. Nếu có $n$ phần tử, và độ dài đường trong là $I(n)$, thì số phép lặp trung bình cho một lần tìm kiếm thành công là $T(n)=1+{\frac {I(n)}{n}}$, trong đó đã cộng thêm một bước lặp ở đầu.

Do tìm kiếm nhị phân là thuật toán tối ưu cho việc tìm kiếm bằng cách so sánh, bài toán được đơn giản hóa thành việc tính độ dài đường đi trong tối thiểu của tất cả cây nhị phân có $n$ nút, tức là bằng:

$I(n)=\sum _{k=1}^{n}\left\lfloor \log _{2}(k)\right\rfloor$

Ví dụ, với một mảng 7 phần tử, phần tử gốc cần một phép lặp, hai phần tử bên dưới gốc cần hai phép lặp, và bốn phần tử dưới nữa gần ba phép lặp. Trong trường hợp này, độ dài đường đi trong là:

$\sum _{k=1}^{7}\left\lfloor \log _{2}(k)\right\rfloor =0+2(1)+4(2)=2+8=10$

Số phép lặp trung bình sẽ là $1+{\frac {10}{7}}=2{\frac {3}{7}}$ dựa theo công thức với trường hợp trung bình. Tổng $I(n)$ có thể rút gọn thành:

$I(n)=\sum _{k=1}^{n}\left\lfloor \log _{2}(k)\right\rfloor =(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2$

Thay $I(n)$ vào phương trình $T(n)$:

$T(n)=1+{\frac {(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2}{n}}=\lfloor \log _{2}(n)\rfloor +1-(2^{\lfloor \log _{2}(n)\rfloor +1}-\lfloor \log _{2}(n)\rfloor -2)/n$

Với $n$ là một số nguyên, phương trình trên tương đương với phương trình trong trường hợp trung bình cho một lần tìm kiếm thành công như đã chỉ ra ở trên.

Tìm kiếm không thành công

Ta có thể biểu diễn lần tìm kiếm không thành công bằng cách thêm vào cây các nút ngoài, tạo thành cây nhị phân mở rộng. Nếu một nút trong, hoặc một nút có trong cây, có ít hơn hai nút con, thì ta sẽ thêm vào các nút con bổ sung, gọi là các nút ngoài, để mỗi nút trong đều có hai nút con. By doing so, an unsuccessful search can be represented as a path to an external node, whose parent is the single element that remains during the last iteration. Đường đi ngoài (external path) là đường đi từ gốc đến một nút ngoài. Độ dài đường đi ngoài (external path length) là tổng độ dài tất cả đường đi ngoài unique. Nếu số phần tử là $n$ ($n$ là số nguyên dương), và độ dài đường đi ngoài là $E(n)$, thì số phép lặp trung bình cho một lần tìm kiếm không thành công là $T'(n)={\frac {E(n)}{n+1}}$, trong đó đã tính một phép lặp lúc đầu. Trong công thức này, ta lấy độ dài đường đi ngoài chia cho $n+1$ chứ không phải $n$ vì có $n+1$ đường đi ngoài biểu diễn cho các khoảng giữa và ngoài các phần tử trong mảng.

Tương tự, bài toán này có thể đơn giản hóa thành bài toán tính độ dài đường đi ngoài tối thiếu của tất cả cây nhị phân có $n$ nút. Với tất cả các cây nhị phân, độ dài đường đi ngoài bằng độ dài đường đi trong cộng với $2n$. Thay $I(n)$ vào ta có:

$E(n)=I(n)+2n=\left[(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2\right]+2n=(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}$

Thay $E(n)$ vào công thức tính $T'(n)$, ta có thể xác định trường hợp trung bình cho những lần tìm kiếm không thành công:

$T'(n)={\frac {(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}}{(n+1)}}=\lfloor \log _{2}(n)\rfloor +2-2^{\lfloor \log _{2}(n)\rfloor +1}/(n+1)$

Hiệu suất của các cách thay thế

Mỗi phép lặp trong cách tìm kiếm nhị phân trên thực hiện một hoặc hai lần so sánh để kiểm tra phần tử ở giữa có bằng với giá trị cần tìm không. Giả sử mỗi phần tử có xác suất được tìm bằng nhau, mỗi phép lặp thực hiện trung bình 1,5 lần so sánh. Một cách làm khác của thuật toán sẽ thực hiện kiểm tra phần tử giữa ở cuối mỗi lần tìm kiếm. Theo cách này, trung bình mỗi phép lặp bỏ qua 0,5 lần so sánh, tiết kiệm thời gian hơn một chút trên mỗi phép lặp ở hầu hết các loại máy tính. Tuy nhiên, cách này lại khiến mỗi lần tìm kiếm luôn phải thực hiện số phép lặp tối đa, trung bình mỗi lần tìm cộng thêm một phép lặp. Vì vòng lặp so sánh chỉ được thực hiện ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$ lần trong trường hợp tệ nhất, the slight increase in efficiency per iteration does not compensate for the extra iteration for all but very large ${\textstyle n}$.

Thời gian chạy và mức sử dụng cache

Trong quá trình phân tích hiệu suất của thuật toán, một vấn đề khác cần lưu ý là thời gian cần để so sánh hai phần tử. Với các số nguyên và chuỗi ký tự, khoảng thời gian này tăng tuyến tính do độ dài mã hóa (thường là số bit) của các phần tử tăng theo. Ví dụ, một cặp số nguyên dương 64 bit sẽ cần phải so sánh số bit gấp đôi so với một cặp số nguyên dương 32 bit. Trường hợp tệ nhất được đạt đến khi hai số nguyên bằng nhau. Điều này có thể đáng lưu tâm khi độ dài mã hóa của các phần tử ở mức lớn, ví dụ như khi so sánh các số thuộc kiểu nguyên lớn hơn hay so sánh các chuỗi ký tự dài, khiến cho việc so sánh rất tốn thời gian. Hơn nữa, so với các số nguyên hoặc chuỗi ký tự ngắn thì so sánh các giá trị dấu phẩy động (cách biểu diễn số thông dụng nhất của số thực) thường còn tốn thời gian hơn..

Trên hầu hết các kiểu kiến trúc máy tính, bộ vi xử lý có bộ nhớ cache riêng tách biệt khỏi RAM. Do nằm ngay trong bộ xử lý, bộ nhớ cache có thể truy cập nhanh hơn nhưng thường chỉ chứa được ít dữ liệu hơn RAM. Do đó, hầu hết các bộ xử lý lưu địa chỉ những vùng bộ nhớ đã được truy cập gần đây và cả những vùng bộ nhớ xung quanh chúng. Ví dụ, khi truy cập vào một phần tử trong mảng, phần tử này, cùng với cả những phần tử được lưu gần đó, có thể được lưu vào trong RAM để sau đó có thể truy cập nhanh hơn được vào các phần tử khác liền kề (tính địa phương trong truy xuất - locality of reference). Với một mảng đã sắp xếp, quá trình tìm kiếm nhị phân có thể phải nhảy sang các vùng bộ nhớ nằm xa nếu mảng có kích thước lớn, không giống như các thuật toán (như tìm kiếm tuyến tính hay dò tuyến tính trong bảng băm) truy cập các phần tử theo thứ tự lần lượt. Điều này làm thời gian chạy của thuật toán tăng lên đôi chút với các mảng lớn trên hầu hết các hệ thống.

Tìm kiếm nhị phân với các hệ thống khác

Áp dụng tìm kiếm nhị phân với các mảng đã được sắp xếp là một giải pháp rất không hiệu quả khi xen giữa các phép chèn và xóa còn là các phép truy hồi, mỗi thao tác đó phải mất ${\textstyle O(n)}$ thời gian để thực hiện. Ngoài ra, yêu cầu phải sắp xếp trước các mảng có thể làm phức tạp việc sử dụng bộ nhớ, đặc biệt là khi các phần tử thường được chèn vào trong mảng. Một số cấu trúc dữ liệu khác có thể hỗ trợ các thao tác chèn và xóa hiệu quả hơn nhiều. Tìm kiếm nhị phân có thể được dùng để thực hiện so khớp chính xác và thao tác quan hệ tập hợp (xác định giá trị cần tìm có phải là một tập hợp nhiều giá trị không). Hai bài toán này cũng có thể được thực hiện nhanh hơn trên các cấu trúc dữ liệu khác. Tuy nhiên, khác với các hệ thống tìm kiếm khác, tìm kiếm nhị phân hiệu quả hơn trong phép so khớp xấp xỉ, thường chỉ thực hiện trong ${\textstyle O(\log n)}$ thời gian bất kể kiểu hay cấu trúc của các giá trị. Ngoài ra còn có một số phép toán, như tìm phần tử nhỏ nhất và lớn nhất, có thể được thực hiện hiệu quả trên mảng đã được sắp xếp.

Tìm kiếm tuyến tính

Tìm kiếm tuyến tính là một thuật toán tìm kiếm đơn giản: nó kiểm tra mọi bản ghi cho tới khi tìm thấy giá trị cần tìm. Tìm kiếm tuyến tính có thể được thực hiện trên danh sách liên kết, cho phép các thao tác chèn và xóa nhanh hơn so với mảng. Tìm kiếm nhị phân nhanh hơn tìm kiếm tuyến tính trên các mảng đã được sắp xếp trừ khi mảng có kích thước nhỏ, mặc dù trước khi tìm kiếm cần phải thực hiện sắp xếp lại mảng trước. Tất cả các thuật toán sắp xếp dựa trên thao tác so sánh các phần tử, như sắp xếp nhanh và sắp xếp trộn, cần ít nhất ${\textstyle O(n\log n)}$ phép so sánh trong trường hợp tệ nhất. Khác với tìm kiếm tuyến tính, tìm kiếm nhị phân có thể được ứng dụng để tìm so khớp xấp xỉ một cách hiệu quả. Một số thao tác như tìm phần tử nhỏ nhất và lớn nhất có thể được thực hiện hiệu quả chỉ khi mảng đã được sắp xếp.

Cây

Phép tìm kiếm trên cây tìm kiếm nhị phân sử dụng một thuật toán tương tự tìm kiếm nhị phân.

Cây tìm kiếm nhị phân là một cấu trúc dữ liệu dạng cây nhị phân hoạt động dựa trên nguyên lý của tìm kiếm nhị phân. Các bản ghi trong cây được biểu diễn theo thứ tự đã được sắp xếp, và mỗi bản ghi có thể được tìm bằng một thuật toán tương tự tìm kiếm nhị phân, thực hiện trung bình theo thời gian logarit. Các phép chèn và xóa cũng cần trung bình thời gian logarit trong cây tìm kiếm nhị phân. Chúng có thể được thực hiện nhanh hơn so với các thao tác chèn và xóa theo thời gian tuyến tính trên các mảng đã được sắp xếp, đồng thời các thao tác có thể thực hiện trên mảng đã được sắp xếp cũng có thể được thực hiện trên cây nhị phân, bao gồm cả các phép truy vấn khoảng và truy vấn xấp xỉ.

Tuy nhiên, tìm kiếm nhị phân thường hiệu quả hơn trong việc tìm kiếm, do các cây nhị phân hầu như đều không cân bằng tuyệt đối, khiến hiệu suất kém hơn đôi chút so với tìm kiếm nhị phân. Điều này thậm chí vẫn áp dụng với các cây tìm kiếm nhị phân tự cân bằng, vì chúng hiếm khi tạo ra cây có số bậc nhỏ nhất có thể. Except for balanced binary search trees, the tree may be severely imbalanced with few internal nodes with two children, resulting in the average and worst-case search time approaching ${\textstyle n}$ comparisons. Cây tìm kiếm nhị phân cần nhiều không gian hơn so với mảng đã được sắp xếp.

Cây tìm kiếm nhị phân hữu ích nhất cho việc tìm kiềm nhanh trong các ổ cứng ngoài, bởi cây tìm kiếm nhị phân có thể được dựng hiệu quả trong các hệ thống tập tin. Cấu trúc B-cây tổng quát hóa phương pháp tổ chức cây này. B-cây thường được dùng để tổ chức các ổ lưu trữ dài hạn như cơ sở dữ liệu và hệ thống tập tin.

Băm

For implementing associative arrays, hash tables, a data structure that maps keys to records using a hash function, are generally faster than binary search on a sorted array of records. Most hash table implementations require only amortized constant time on average. However, hashing is not useful for approximate matches, such as computing the next-smallest, next-largest, and nearest key, as the only information given on a failed search is that the target is not present in any record. Binary search is ideal for such matches, performing them in logarithmic time. Binary search also supports approximate matches. Some operations, like finding the smallest and largest element, can be done efficiently on sorted arrays but not on hash tables.

Các thuật toán quan hệ tập hợp

Một vấn đề liên quan tới tìm kiếm là quan hệ tập hợp. Bất cứ thuật toán nào thực hiện tra cứu, như tìm kiếm nhị phân, cũng có thể dùng cho quan hệ tập hợp. Một số thuật toán khác được thiết kế phù hợp hơn với quan hệ tập hợp. Mảng bit là cách làm đơn giản nhất, thường được dùng khi số khóa bị giới hạn. It compactly stores a collection of bits, with each bit representing a single key within the range of keys. Bit arrays are very fast, requiring only ${\textstyle O(1)}$ time. The Judy1 type of Judy array handles 64-bit keys efficiently.

For approximate results, Bloom filters, another probabilistic data structure based on hashing, store a set of keys by encoding the keys using a bit array and multiple hash functions. Bloom filters are much more space-efficient than bit arrays in most cases and not much slower: with ${\textstyle k}$ hash functions, membership queries require only ${\textstyle O(k)}$ time. However, Bloom filters suffer from false positives.

Các cấu trúc dữ liệu khác

Còn có các cấu trúc dữ liệu khác có thể cải thiện tìm kiếm nhị phân trong một số trường hợp với cả mục đích tìm kiếm lẫn các thao tác khác có thể được thực hiện trên các mảng đã được sắp xếp. Ví dụ, các phép tìm kiếm, so khớp xấp xỉ và các thao tác khác trên mảng đã được sắp xếp có thể được thực hiện hiệu quả hơn tìm kiếm nhị phân nếu áp dụng trên các cấu trúc dữ liệu chuyên biệt như cây van Emde Boas, fusion trees, trie và mảng bit. Các cấu trúc dữ liệu chuyên biệt này thường chỉ nhanh hơn vì chúng sử dụng các tính chất của những khóa có điều kiện nhất định (thông thường những khóa này là các số nguyên nhỏ), và do đó thời gian chạy hoặc không gian cần sử dụng có thể lớn nếu không đáp ứng được các điều kiện ấy. As long as the keys can be ordered, these operations can always be done at least efficiently on a sorted array regardless of the keys. Some structures, such as Judy arrays, use a combination of approaches to mitigate this while retaining efficiency and the ability to perform approximate matching.

Biến thể

Uniform binary search

Bài chi tiết: Uniform binary search

Uniform binary search stores the difference between the current and the two next possible middle elements instead of specific bounds.

Uniform binary search stores, instead of the lower and upper bounds, the difference in the index of the middle element from the current iteration to the next iteration. A lookup table containing the differences is computed beforehand. For example, if the array to be searched is [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11], the middle element ($m$) would be 6. In this case, the middle element of the left subarray ([1, 2, 3, 4, 5]) is 3 and the middle element of the right subarray ([7, 8, 9, 10, 11]) is 9. Uniform binary search would store the value of 3 as both indices differ from 6 by this same amount. To reduce the search space, the algorithm either adds or subtracts this change from the index of the middle element. Uniform binary search may be faster on systems where it is inefficient to calculate the midpoint, such as on decimal computers.

Tìm kiếm mũ

Bài chi tiết: Exponential search

Visualization of exponential searching finding the upper bound for the subsequent binary search

Exponential search extends binary search to unbounded lists. It starts by finding the first element with an index that is both a power of two and greater than the target value. Afterwards, it sets that index as the upper bound, and switches to binary search. A search takes ${\textstyle \lfloor \log _{2}x+1\rfloor }$ iterations before binary search is started and at most ${\textstyle \lfloor \log _{2}x\rfloor }$ iterations of the binary search, where ${\textstyle x}$ is the position of the target value. Exponential search works on bounded lists, but becomes an improvement over binary search only if the target value lies near the beginning of the array.

Tìm kiếm nội suy

Bài chi tiết: Tìm kiếm nội suy

Visualization of interpolation search using linear interpolation. In this case, no searching is needed because the estimate of the target's location within the array is correct. Other implementations may specify another function for estimating the target's location.

Instead of calculating the midpoint, interpolation search estimates the position of the target value, taking into account the lowest and highest elements in the array as well as length of the array. It works on the basis that the midpoint is not the best guess in many cases. For example, if the target value is close to the highest element in the array, it is likely to be located near the end of the array.

A common interpolation function is linear interpolation. If $A$ is the array, $L,R$ are the lower and upper bounds respectively, and $T$ is the target, then the target is estimated to be about $(T-A_{L})/(A_{R}-A_{L})$ of the way between $L$ and $R$. When linear interpolation is used, and the distribution of the array elements is uniform or near uniform, interpolation search makes ${\textstyle O(\log \log n)}$ comparisons.

In practice, interpolation search is slower than binary search for small arrays, as interpolation search requires extra computation. Its time complexity grows more slowly than binary search, but this only compensates for the extra computation for large arrays.

Đổ xuống một phần

Bài chi tiết: Fractional cascading

In fractional cascading, each array has pointers to every second element of another array, so only one binary search has to be performed to search all the arrays.

Fractional cascading is a technique that speeds up binary searches for the same element in multiple sorted arrays. Searching each array separately requires ${\textstyle O(k\log n)}$ time, where ${\textstyle k}$ is the number of arrays. Fractional cascading reduces this to ${\textstyle O(k+\log n)}$ by storing specific information in each array about each element and its position in the other arrays.

Fractional cascading was originally developed to efficiently solve various computational geometry problems. Fractional cascading has been applied elsewhere, such as in data mining and Internet Protocol routing.

Generalization to graphs

Binary search has been generalized to work on certain types of graphs, where the target value is stored in a vertex instead of an array element. Binary search trees are one such generalization—when a vertex (node) in the tree is queried, the algorithm either learns that the vertex is the target, or otherwise which subtree the target would be located in. However, this can be further generalized as follows: given an undirected, positively weighted graph and a target vertex, the algorithm learns upon querying a vertex that it is equal to the target, or it is given an incident edge that is on the shortest path from the queried vertex to the target. The standard binary search algorithm is simply the case where the graph is a path. Similarly, binary search trees are the case where the edges to the left or right subtrees are given when the queried vertex is unequal to the target. For all undirected, positively weighted graphs, there is an algorithm that finds the target vertex in $O(\log n)$ queries in the worst case.

Noisy binary search

In noisy binary search, there is a certain probability that a comparison is incorrect.

Noisy binary search algorithms solve the case where the algorithm cannot reliably compare elements of the array. For each pair of elements, there is a certain probability that the algorithm makes the wrong comparison. Noisy binary search can find the correct position of the target with a given probability that controls the reliability of the yielded position. Every noisy binary search procedure must make at least $(1-\tau ){\frac {\log _{2}(n)}{H(p)}}-{\frac {10}{H(p)}}$ comparisons on average, where $H(p)=-p\log _{2}(p)-(1-p)\log _{2}(1-p)$ is the binary entropy function and $\tau$ is the probability that the procedure yields the wrong position. The noisy binary search problem can be considered as a case of the Rényi-Ulam game, a variant of Twenty Questions where the answers may be wrong.

Tìm kiếm nhị phân lượng tử

Classical computers are bounded to the worst case of exactly ${\textstyle \lfloor \log _{2}n+1\rfloor }$ iterations when performing binary search. Quantum algorithms for binary search are still bounded to a proportion of ${\textstyle \log _{2}n}$ queries (representing iterations of the classical procedure), but the constant factor is less than one, providing for a lower time complexity on quantum computers. Any exact quantum binary search procedure—that is, a procedure that always yields the correct result—requires at least ${\textstyle {\frac {1}{\pi }}(\ln n-1)\approx 0.22\log _{2}n}$ queries in the worst case, where ${\textstyle \ln }$ is the natural logarithm. There is an exact quantum binary search procedure that runs in ${\textstyle 4\log _{605}n\approx 0.433\log _{2}n}$ queries in the worst case. In comparison, Grover's algorithm is the optimal quantum algorithm for searching an unordered list of elements, and it requires $O({\sqrt {n}})$ queries.

Lịch sử

Ý tưởng về việc sắp xếp một danh sách để tìm kiếm được nhanh hơn đã có từ thời cổ xưa. Ví dụ được biết tới sớm nhất là tấm bảng của Inakibit-Anu từ thời Babylon vào k. 200 TCN. Tấm bảng này chứa khoảng 500 con số ở hệ thập lục phân và các số nghịch đảo của chúng được sắp xếp theo thứ tự từ điển, khiến việc tìm kiếm dễ dàng hơn. Ngoài ra trên Quần đảo Aegean còn phát hiện được một vài danh sách những cái tên được sắp xếp theo chữ cái đầu tiên. Catholicon, một cuốn từ điển Latin được hoàn thành vào năm 1286 SCN, là tác phẩm đầu tiên mô tả các quy tắc sắp xếp các từ theo thứ tự bảng chữ cái, thay vì chỉ theo vài ký tự đầu tiên.

Vào năm 1946, John Mauchly là người đầu tiên nhắc tới tìm kiếm nhị phân trong Moore School Lectures, một khóa học về máy tính tại Trường Kỹ thuật Điện tử Moore, Đại học Pennsylvania. Năm 1957, William Wesley Peterson xuất bản phương pháp đầu tiên cho giải thuật tìm kiếm nội suy. Mọi thuật toán tìm kiếm nhị phân đã được xuất bản chỉ hoạt động với các mảng có độ dài ở dạng $2^{\alpha }-1$ cho tới năm 1960, khi Derrick Henry Lehmer cho xuất bản một thuật toán tìm kiếm nhị phân có thể hoạt động với mọi mảng. Năm 1962, Hermann Bottenbruch trình bày thuật toán tìm kiếm nhị phân được áp dụng bằng ngôn ngữ ALGOL 60, trong đó bước kiểm tra phần tử giữa được đưa xuống cuối, làm tăng số phép lặp trung bình thêm một, nhưng giảm được một bước so sánh mỗi phép lặp. Thuật toán uniform binary search được phát triển bởi A. K. Chandra tại Đại học Stanford vào năm 1971. Năm 1986, Bernard Chazelle và Leonidas J. Guibas giới thiệu phương pháp đổ xuống một phần (fractional cascading) nhằm giải quyết nhiều vấn đề về tìm kiếm trong hình học tính toán.

Thư viện hỗ trợ

Nhiều thư viện chuẩn của các ngôn ngữ có các chương trình con thực hiện tìm kiếm nhị phân:

• C cung cấp hàm bsearch() trong thư viện chuẩn, which is typically implemented via binary search, although the official standard does not require it so.
• Standard Template Library của C++ cung cấp các hàm binary_search(), lower_bound(), upper_bound() và equal_range().
• COBOL cung cấp động từ SEARCH ALL có chức năng thực hiện tìm kiếm nhị phân trên các bảng được sắp xếp trong COBOL.
• Gói thư viện chuẩn sort của Go cung cấp các hàm Search, SearchInts, SearchFloat64s, và SearchStrings, lần lượt có chức năng thực hiện tìm kiếm nhị phân tổng quát, tìm kiếm các lát số nguyên, số thập phân dấu phẩy động và chuỗi ký tự.
• Java cung cấp một bộ các phương thức static chồng binarySearch() trong các lớp Arrays và Collections chứa trong gói java.util chuẩn, lần lượt có chức năng thực hiện tìm kiếm nhị phân trên các mảng trong Java và trên các List.
• Microsoft's .NET Framework 2.0 offers static generic versions of the binary search algorithm in its collection base classes. An example would be System.Array's method BinarySearch<T>(T[] array, T value).
• Với Objective-C, framework Cocoa cung cấp phương thức NSArray -indexOfObject:inSortedRange:options:usingComparator: trong Mac OS X từ bản 10.6 trở lên. Framework Core Foundation C của Apple cũng chứa hàm CFArrayBSearchValues().
• Python cung cấp mô đun bisect.
• Lớp Array của Ruby có chứa phương thức bsearch có cả chức năng so khớp xấp xỉ.

Ghi chú và tham khảo

Tài liệu

• Bentley, Jon (2000). Programming pearls (ấn bản 2). Addison-Wesley. ISBN 978-0-201-65788-3.Quản lý CS1: ref=harv (liên kết)
• Butterfield, Andrew; Ngondi, Gerard E. (2016). A dictionary of computer science (ấn bản 7). Oxford, UK: Oxford University Press. ISBN 978-0-19-968897-5.Quản lý CS1: ref=harv (liên kết)
• Chang, Shi-Kuo (2003). Data structures and algorithms. Software Engineering and Knowledge Engineering. 13. Singapore: World Scientific. ISBN 978-981-238-348-8.Quản lý CS1: ref=harv (liên kết)
• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009). Introduction to algorithms (ấn bản 3). MIT Press and McGraw-Hill. ISBN 978-0-262-03384-8.Quản lý CS1: ref=harv (liên kết)
• Fitzgerald, Michael (2007). Ruby pocket reference. Sebastopol, California: O'Reilly Media. ISBN 978-1-4919-2601-7.Quản lý CS1: ref=harv (liên kết)
• Goldman, Sally A.; Goldman, Kenneth J. (2008). A practical guide to data structures and algorithms using Java. Boca Raton, Florida: CRC Press. ISBN 978-1-58488-455-2.Quản lý CS1: ref=harv (liên kết)
• Kasahara, Masahiro; Morishita, Shinichi (2006). Large-scale genome sequence processing. London, UK: Imperial College Press. ISBN 978-1-86094-635-6.Quản lý CS1: ref=harv (liên kết)
• Knuth, Donald (1997). Fundamental algorithms. The Art of Computer Programming. 1 (ấn bản 3). Reading, MA: Addison-Wesley Professional. ISBN 978-0-201-89683-1.Quản lý CS1: ref=harv (liên kết)
• Knuth, Donald (1998). Sorting and searching. The Art of Computer Programming. 3 (ấn bản 2). Reading, MA: Addison-Wesley Professional. ISBN 978-0-201-89685-5.Quản lý CS1: ref=harv (liên kết)
• Knuth, Donald (2011). Combinatorial algorithms. The Art of Computer Programming. 4A (ấn bản 1). Reading, MA: Addison-Wesley Professional. ISBN 978-0-201-03804-0.Quản lý CS1: ref=harv (liên kết)
• Moffat, Alistair; Turpin, Andrew (2002). Compression and coding algorithms. Hamburg, Germany: Kluwer Academic Publishers. doi:10.1007/978-1-4615-0935-6. ISBN 978-0-7923-7668-2.Quản lý CS1: ref=harv (liên kết)
• Sedgewick, Robert; Wayne, Kevin (2011). Algorithms (ấn bản 4). Upper Saddle River, New Jersey: Addison-Wesley Professional. ISBN 978-0-321-57351-3.Quản lý CS1: ref=harv (liên kết) Condensed web version ; book version .
• Stroustrup, Bjarne (2013). The C++ programming language (ấn bản 4). Upper Saddle River, New Jersey: Addison-Wesley Professional. ISBN 978-0-321-56384-2.Quản lý CS1: ref=harv (liên kết)