Đáp ứng xung
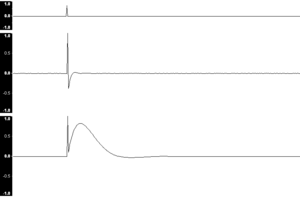
Đáp ứng xung của một hệ thống, như hệ thống cơ học hay hệ thống điện tử, là các quá trình biến đổi trạng thái của hệ thống đó sau khi có tác động vào bởi một xung, thường được mô hình hóa là hàm delta.
Ví dụ, việc gõ vào mặt trống là tác động của một xung vào hệ thống cơ học là cái trống, và đáp ứng của hệ thống là dao động tắt dần của mặt trống, phát ra âm thanh. Một ví dụ khác là một hệ điện tử có đầu vào và đầu ra, nhận tín hiệu vào là một xung điện áp, tín hiệu cho ra lúc này chính là đáp ứng xung của hệ thống điện tử.
Cơ sở toán học[sửa | sửa mã nguồn]
Về mặt toán học, một xung có thể được mô hình hóa là một hàm delta, như hàm delta Dirac hay hàm delta Kronecker. Giả sử hệ thống, được cọi là một hộp đen có toán tử T, biến đổi đầu vào x[n] thành đầu ra y[n]:
T là tác vụ tác động lên một chuỗi đầu vào và cho ra một chuỗi đầu ra. T có thể là phi tuyến, ví dụ: hay tuyến tính, ví dụ: .
Giả sử T là tuyến tính:
và
Giả sử T là bất biến dưới các phép biến đổi tịnh tiến, nghĩa là: nếu thì . Với một hệ thống như vậy, thì bất kì đầu ra nào cũng có thể được tính toán dựa trên 2 yếu tố: đầu vào và một chuỗi gọi là đáp ứng xung (chúng đặc trưng cho tính chất của hệ thống một cách đầy đủ). Cụ thể:
và áp dụng T lên hai phía
Vì T là tuyến tính và bất biến với phép tịnh tiến
Vì đầu ra y[k] cho bởi ta có thể viết lại
Đặt
ta có kết quả cuối cùng
Chuỗi chính là đáp ứng xung của hệ thống đó. Và h[n] cũng chính là đầu ra của hệ thống khi đầu vào là hàm delta Kronecker. Kết quả tương tự với hệ thống thời gian liên tục.
Xem thêm[sửa | sửa mã nguồn]
- Hàm delta Kronecker
- Hàm delta Dirac
- Hàm delta
- Hàm Green
- Đáp ứng tần
- Lý thuyết hệ thống LTI
- Phân tích hệ thống
- Hàm truyền

![{\displaystyle y\left[n\right]=T\left[x\left[n\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/961a3a1d05ccd51e9e745cccba0587316bcea35c)
![{\displaystyle T\left[x\left[n\right]\right]=x^{2}\left[n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff343f065eb62e3fb28540132ee7d31fc6b54517)
![{\displaystyle T\left[x\left[n\right]\right]=x\left[n-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6497a9f44ac48336346e200f45ae38eca594ba7)
![{\displaystyle T\left[x\left[n\right]+y\left[n\right]\right]=T\left[x\left[n\right]\right]+T\left[y\left[n\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bb10e1490efed5d3cb2cb8ab77b18830016ea94)
![{\displaystyle T\left[\lambda x\left[n\right]\right]=\lambda T\left[x\left[n\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63fdebe8fbf006f78b0e66957516e61c4a862a6f)
![{\displaystyle y\left[n-k\right]=T\left[x\left[n-k\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cc23b07dde0c70a34f6659e15e007f9d168d056)
![{\displaystyle x\left[n\right]=\sum _{k}x\left[k\right]\delta \left[n-k\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e66c6823c79306bddc3b22dd65a2ff1167711c5)
![{\displaystyle T\left[x\left[n\right]\right]=T\left[\sum _{k}x\left[k\right]\delta \left[n-k\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f508325ee76dd413eb06138c6e482b1cdc7f0c06)
![{\displaystyle T\left[x\left[n\right]\right]=\sum _{k}x\left[k\right]T\left[\delta \left[n-k\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/728cee592f6bdfaa7cd5eb88772e25273545c66c)
![{\displaystyle y\left[k\right]=T\left[x\left[k\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe69e082b8b2f9d45a67add6f059606cf956770e)
![{\displaystyle y\left[n\right]=\sum _{k}x\left[k\right]T\left[\delta \left[n-k\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/370368ee80b3aa1f901d8054b3dcfed3b6454792)
![{\displaystyle h\left[n-k\right]=T\left[\delta \left[n-k\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73f14d5e48430f542d820689030f0f2499972a15)
![{\displaystyle y\left[n\right]=\sum _{k}x\left[k\right]h\left[n-k\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60cda1b57b2b9c701ea3d7a3f69cee5c77da0e0b)
![{\displaystyle h\left[n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb4920cd26625cc4532f981c9ac79942d0efca00)