Điện trường
Bài này không có nguồn tham khảo nào. |
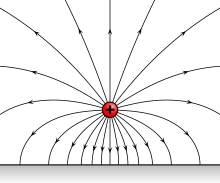
Điện trường là một trường điện tạo ra từ các đường lực điện bao quanh lấy điện tích. Điện trường có thể được biểu diễn bằng các đường sức điện. Vector cường độ điện trường tại bất kì điểm nào trên đường sức điện có phương trùng với tiếp tuyến tại điểm đó trên đường sức điện và có chiều trùng với chiều của đường sức. Tập hợp các đường sức cường độ điện trường gọi là điện phổ.
Điện trường rất quan trọng trong nhiều lĩnh vực vật lý và được khai thác thực tế trong công nghệ điện. Ở quy mô nguyên tử, điện trường là lực tương tác chính giữa hạt nhân và các electron trong nguyên tử. Điện trường và từ trường đều là biểu hiện của lực điện từ, một trong bốn lực cơ bản (hoặc tương tác cơ bản) của tự nhiên.
Cường độ điện trường[sửa | sửa mã nguồn]
Cường độ điện trường là đại lượng đặc trưng cho điện trường về phương diện tác dụng lực. Một điện tích, q, nằm trong điện trường có cường độ điện trường, thể hiện bằng vectơ , chịu lực tĩnh điện, thể hiện bằng vector lực , tính theo biểu thức:
Vậy,
Cường độ điện trường gây ra bởi điện tích điểm được tính bằng công thức:
trong đó
- q là độ lớn điện tích
- là độ điện thẩm chân không
- là hằng số điện môi của môi trường
- r là khoảng cách từ điện tích đến điểm ta xét
Với cường độ điện trường này, một điện tích khác nằm trong nó sẽ chịu lực điện tỷ lệ thuận với tích hai điện tích và tỷ lệ nghịch với bình phương khoảng cách. Đó chính là lực Coulomb.
Để tính được điện trường do một vật mang điện (điện tích) gây ra, có thể chia nó ra thành nhiều vật nhỏ hơn. Nếu phép chia tiến đến một giới hạn nào đó, vật nhỏ mang điện sẽ trở thành một điện tích. Khi đó có thể áp dụng nguyên lý chồng chất cho điện trường (hay còn gọi là nguyên lý tác dụng độc lập).
Cường độ điện trường tại một điểm trong điện trường do N điện tích điểm gây ra bằng tổng vectơ cường độ điện trường do từng điện tích điểm gây ra tại điểm đó.
Cường độ điện trường của vật dẫn điện[sửa | sửa mã nguồn]
Điện tích điểm hình cầu[sửa | sửa mã nguồn]
Cường độ điện trường của một hình cầu tròn có diện tích
Cường độ điện lượng
Điện tích khác loại có cùng điện lượng[sửa | sửa mã nguồn]
Lực Coulomb của 2 điện tích khác loại có cùng điện lượng
- . ()
Lực này tương tác với điện tích tạo ra điện trường
Tụ điện[sửa | sửa mã nguồn]
Tụ điện tạo ra từ 2 bề mặt song song có cường độ điện trường
Định luật Gauss về Điện trường[sửa | sửa mã nguồn]
Định luật Gauss dưới dạng Tích phân[sửa | sửa mã nguồn]
Với
- là thông lượng điện,
- là điện trường,
- là diện tích của mặt gauss vi phân trên mặt đóng S,
- là điện tích được bao bởi mặt đó,
- là mật độ điện tích tại một điểm trong
- , là hằng số điện của không gian tự do và là tích phân trên mặt S bao phủ thể tích V.
Định luật Gauss dưới dạng vi phân[sửa | sửa mã nguồn]
Với
- là toán tử div,
- là điện trường,
- ρ là mật độ điện tích (đơn vị C/m³),
Tham khảo[sửa | sửa mã nguồn]
Liên kết ngoài[sửa | sửa mã nguồn]
- Trường tĩnh điện: Liên hệ giữa cường độ điện trường và điện thế Lưu trữ 2006-11-02 tại Wayback Machine tại Giáo trình điện tử, Đại học Cần Thơ.





























