Phương hướng
Bài viết hoặc đoạn này cần người am hiểu về chủ đề này trợ giúp biên tập mở rộng hoặc cải thiện. |
Trong hình học, phương hướng hay đơn giản là hướng của một vật thể như một đường thẳng, mặt phẳng hoặc một vật thể rắn khác là một trong những khái niệm được dùng để miêu tả không gian mà vật đó chiếm giữ.[1] Hãy thử tưởng tượng khi di chuyển 1 vật từ vị trí tham chiếu đến vị trí cụ thể cũng giống như chuyển động quay. Tuy nhiên chỉ chuyển động quay có thể không tiếp cận với vị trí hiện tại. Có lẽ sẽ cần thêm một phép tịnh tiến được gọi là vị trí hay tọa độ. Vị trí và phương hướng có thể miêu tả hoàn toàn việc vật được đặt như thế nào trong không gian. Những chuyển động quay và sự tịnh tiến có trong tưởng tượng có thể thay đổi, nhưng phương hướng của vật thể không thay đổi theo dù tịnh tiến thay đổi, và địa điểm của vật thể cũng không thay đổi khi vật quay.
Về cơ bản, phương hướng được đặt ra dựa trên khung tham chiếu, thường được sử dụng bở hế thống tọa độ Cartesian.
Biểu diễn trong toán học[sửa | sửa mã nguồn]
Trong không gian 2 chiều[sửa | sửa mã nguồn]
Trong không gian hai chiều thì phương hướng của bất kỳ vật thể (đường thẳng, vector hoặc một mặt phẳng) được đo bởi một giá trị duy nhất: góc được tạo bởi sau khi vật quay. Chỉ có một bậc tự do và một điểm cố định duy nhất về vị trí vật sẽ quay.
Trong không gian 3 chiều[sửa | sửa mã nguồn]
Vị trí và phương hướng trong không gian của một vật thể rắn được xác định như một vị trí và phương hướng của một khung tham chiếu chính trong một khung tham chiếu khác cố định với vật thể, tịnh tiến và quay với nó(khung tham chiếu cố định của vật hoặc hệ tọa độ của vật). Ít nhất 3 giá trị độc lập là cần thiết để miêu tả phưoớng của khung hình cố định. 3 giá trị khác cần thiết để miêu tả vị trí của vật. Mặc dù một vật thể rắn có thể di chuyển tự do được gọi là 6 bậc của tự do.
Mọi điểm trong vật thay đổi vị trí khi chuyển quay diễn ra ngoại trừ các điểm nằm trên trục quay. Nếu vật thể rắn có một chuyển động quay đối xứng thì không phải mọi phương hướng đểu có thể phân biệt được, ngoại trừ khi quan sát các phướng hướng xuất phát từ một phương hướng đã được xác định. Ví dụ, phướng hướng của một đường thẳng, đoạn thằng hoặc vector có được xác định với chỉ hai giá trị, như hướng của 2 hàm Cosin, một ví dụ khác là vị trí của một điểm trên mặt đất thường được miêu tả bằng cách sử dụng phương hướng của đường thẳng giao nhau với tâm của mặt đất, được đo bởi hai góc của kinh tuyến và vĩ tuyến. Đồng thời, phương hướng của một mặt phẳng cũng có thể được miêu tả bởi 2 giá trị, bằng cách xác định phướng của một đường thẳng với mặt phẳng.
Vật thể rắn trong không gian 3 chiều[sửa | sửa mã nguồn]
Góc Euler[sửa | sửa mã nguồn]

Leonhard Euler là người cố gắng biểu diễn phương hướng đầu tiên. Ông đã tưởng tượng ra 3 khung tham chiếu có thể quay lần lượt vòng quanh nhau và nhận ra rằng bằng cách sử dụng một khung tham chiếu cố định và biểu diễn ba vòng quay ông có thể dùng bất kỳ khung tham chiếu trong không gian (sử dụng 2 vòng quay trên một trục dọc cố định và những vòng quay khác trên 2 trục khác). Giá trị của 3 vòng quay được gọi là Góc Euler.

Góc Tait-Bryan[sửa | sửa mã nguồn]
Có ba góc được gọi là các momen đảo lại, dọc-xuống, nghiêng (yaw, pitch and roll), Góc đinh hướng và góc Cardan. Theo toán học mà nói, thì chúng tạo thành một dãy gồm 6 điều có thể xảy trong dãy 12 điều có thể của Định lý góc Euler. Theo thứ tự từ những điều mà miêu tả tốt nhất phương của một phương tiện như máy bay. Trong ngành hàng không vũ trị thì chúng thường được gọi là một góc Euler.

Vector phương hướng[sửa | sửa mã nguồn]
Euler cũng nhận ra rằng thành phần của hai chuyển động quay tương đương với một chuyển quay duy nhất theo các trục cố định (theo định lý về chuyển động quay của Euler). Vậy nên thành phần của 3 góc phải bằng với 1 chuyển động quay duy nhất theo trục được dùng tính toán đến khi ma trận ra đời.
Dựa trên những điều này, ông đưa ra một vector để miêu ra mọi chuyển động quay, với một vector trên trục quay và bằng với giá trị của góc. Vậy nên mọi phương hướng có thể biểu diễn bằng vector quay (được gọi là Vector Euler) có thể dẫn đến một điểm nào đó từ khung tham chiếu. Khi sử đụng để biểu diễn một phương hướng vector quay được sử dụng nhiều nhất được gọi là vector phương hướng.
Ma trận phương hướng[sửa | sửa mã nguồn]
Với sự ra đời của ma trận Định lý Euler đã được viết lại. Chuyển động quay được miêu tả bởi ma trận trực giao cũng được gọi là ma trận quay hoặc ma trận định hướng cosin. Khi biểu diễn một ma trận quay thường được gọi là ma trận phương hướng.
Chứng minh trên đã nhắc đến vector Euler là eigenvecror của một ma trận xoay. Kết quả của 2 ma trận ma trận xoay mà thành phần của chuyển động xoay. Vậy nên phương hướng có thể hiểu rằng chuyern động quay từ khung đầu tiên đê đạt được cái khung mà chúng ta muốn miêu tả.
Không gian cấu hình của một vật không đối xứng trong một không gian n-chiều là SO(n) x Rn. Phương hướng có thể hiểu được là bằng cách gắn một nền tảng của các vector tiếp tuyến vào vật. Phương hướng được xác định các hướng đường của các điểm của vector.
Phương hướng quaternion[sửa | sửa mã nguồn]
Một cách khác để miêu tả chuyển động quay là sử dụng chuyển động quaternion, thường được gọi là versors. Chúng tương đương với ma trận quay và ma trận vectors. Đối với vector quay, chúng có thể dễ dàng được chuyển đổi thành ma trận và ngược lại. Khi dùng để biểu diễn phương hướng, chuyển động quay quaternion thường được gọi là phương hướng quaternions.
Mặt phẳng trong không gian 3 chiều[sửa | sửa mã nguồn]
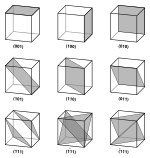
Chỉ số Miller[sửa | sửa mã nguồn]
Hình dáng của mặt phẳng lattice là phương hướng của đường thẳng với mặt phẳng [2] và được miêu tả bởi chỉ số Miller trên mặt phẳng. Trong 3 không gian, một nhóm mặt phẳng (một dãy mặt phẳng liên tiếp) có thể được ký hiểu bằng chỉ số Miller (hkl)[3][4], vậy nhóm mặt phẳng có một hình dáng giống với tất cả thành phần của mặt phẳng.
Tham khảo[sửa | sửa mã nguồn]
- ^
Robert J. Twiss, Eldridge M. Moores (1992). “§2.1 The orientation of structures”. Structural geology (ấn bản 2). Macmillan. tr. 11. ISBN 0-7167-2252-6.
...the attitude of a plane or a line — that is, its orientation in space — is fundamental to the description of structures.
- ^ William Anthony Granville (1904). “§178 Normal line to a surface”. Elements of the differential and integral calculus. Ginn & Company. tr. 275.
- ^ Augustus Edward Hough Love (1892). A treatise on the mathematical theory of elasticity, Volume 1. Cambridge University Press. tr. 79 ff.
- ^ Marcus Frederick Charles Ladd, Rex Alfred Palmer (2003). “§2.3 Families of planes and interplanar spacings”. Structure determination by X-ray crystallography . Springer. tr. 62 ff. ISBN 0-306-47454-9.
