Khác biệt giữa bản sửa đổi của “Hình vành khăn”
Không có tóm lược sửa đổi |
|||
| Dòng 1: | Dòng 1: | ||
[[Tập tin:Annulus area.svg|phải|150x150px|Một hình vành khăn]] |
[[Tập tin:Annulus area.svg|phải|150x150px|Một hình vành khăn]] |
||
[[Tập tin:Mamikon annulus area visualisation.svg|nhỏ|Hình minh họa theo phương pháp [[ |
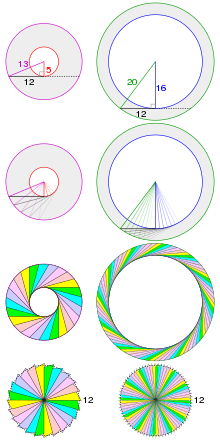
[[Tập tin:Mamikon annulus area visualisation.svg|nhỏ|Hình minh họa theo phương pháp [[vi tích phân trực quan]] của Mamikon cho thấy [[diện tích]] của hai hình vành khăn có cùng độ dài [[dây cung]] lớn nhất là bằng nhau với mọi [[bán kính]] trong và ngoài.<ref>{{Chú thích sách|url=https://books.google.com/books?id=I9oVP8TlyqIC&pg=PA70|tựa đề=The Edge of the Universe: Celebrating Ten Years of Math Horizons|tác giả=|họ=Haunsperger|tên=Deanna|họ 2=Kennedy|tên 2=Stephen|năm=2006|nhà xuất bản=MAA|ngày truy cập=ngày 29 tháng 4 năm 2020}}</ref>]] |
||
Trong [[toán học]], '''hình vành khăn''' ( |
Trong [[toán học]], '''hình vành khăn''' ({{lang-en|annulus}}, từ [[tiếng Latinh]] {{lang|la|anulus}} / {{lang|la|annulus}}, có nghĩa là "chiếc nhẫn nhỏ", số nhiều là {{lang|la|anuli}} / {{lang|la|annuli}}) là một vật hình nhẫn, phần mặt phẳng nằm giữa hai đường tròn đồng tâm.<ref>{{Chú thích sách|url=https://books.google.com/books?id=XIj4DAAAQBAJ|title=Indian Mathematics: Engaging With The World From Ancient To Modern Times|last=Gheverghese|first=Joseph George|date=28 tháng 7 năm 2016|publisher=World Scientific|year=|isbn=1786340631|location=|pages=239|access-date=ngày 6 tháng 5 năm 2020}}</ref><ref>{{Chú thích sách|title=Statics and Analytical Geometry|last=Matthews|first=Bennie|date=21 tháng 6 năm 2019|publisher=Scientific e-Resources|year=|isbn=1839473339|location=|pages=68|chapter=Circle|access-date=ngày 6 tháng 5 năm 2020|chapter-url=https://books.google.com/books?id=xePEDwAAQBAJ&pg=PA68#v=onepage&q&f=false}}</ref> |
||
Những hình vành khăn mở [[Phép đồng phôi|tương đương |
Những hình vành khăn mở [[Phép đồng phôi|tương đương tô pô]] với cả [[Hình trụ tròn|hình trụ]] mở {{Math|''S''<sup>1</sup> × (0,1)}} và [[mặt phẳng thủng]] ({{lang|en|punctured plane}}).<ref>{{Chú thích sách|title=Art of Mathematics|last=Hong|first=Weihu|date=15 tháng 12 năm 2016|publisher=Dorrance Publishing|year=|isbn=1480930180|location=|pages=12|chapter=Surface of Cylinder|access-date=ngày 6 tháng 5 năm 2020|chapter-url=https://books.google.com/books?id=Bfb4DQAAQBAJ&pg=PA12#v=onepage&q&f=false}}</ref> |
||
== Diện tích == |
|||
Diện tích hình vành khăn là hiệu của diện tích [[Đường tròn|hình tròn]] lớn bán kính {{Math|''R''}} với diện tích hình tròn nhỏ bán kính {{Math|''r''}}: |
|||
Diện tích hình vành khăn là hiệu của diện tích [[Đường tròn|hình tròn]] lớn bán kính {{Math|''R''}} với diện tích hình tròn nhỏ bán kính {{Math|''r''}}:<ref>{{Chú thích web|url=https://www.brightstorm.com/math/geometry/area/area-of-an-annulus/|tựa đề=Area of an Annulus|tác giả=|họ=|tên=|ngày=|website=Brightstorm|url lưu trữ=https://web.archive.org/web/20150905064131/http://www.brightstorm.com/math/geometry/area/area-of-an-annulus/|ngày lưu trữ=ngày 5 tháng 9 năm 2019|url hỏng=no|ngày truy cập=ngày 6 tháng 5 năm 2020}}</ref> |
|||
: |
:<math>A = \pi R^2 - \pi r^2 = \pi\left(R^2 - r^2\right).</math> |
||
Diện tích hình vành khăn được xác định dựa vào độ dài của [[đoạn thẳng]] dài nhất trong hình, |
Diện tích hình vành khăn được xác định dựa vào độ dài của [[đoạn thẳng]] dài nhất trong hình, tức dây cung [[tiếp tuyến]] với đường tròn phía trong,<ref>{{Chú thích sách|title=Discrete Geometry for Computer Imagery: 14th IAPR International Conference, DGCI 2008, Lyon, France, April 16-18, 2008, Proceedings|last=|first=|date=5 tháng 4 năm 2008|publisher=Springer|year=|isbn=3540791264|editor-last=Coeurjolly|editor-first=David|location=|pages=464|chapter=The Limits of the Approach|access-date=ngày 6 tháng 5 năm 2020|editor-last2=Sivignon|editor-first2=Isabelle|editor-last3=Tougne|editor-first3=Laure|editor-last4=Dupont|editor-first4=Florent|chapter-url=https://books.google.com/books?id=VNFsCQAAQBAJ&pg=PA464#v=onepage&q&f=false}}</ref> có độ dài {{Math|2''d''}} như hình minh họa. Có thể thể hiện phân tích này bằng [[định lý Pythagoras]] vì đoạn thẳng này tiếp tuyến với đường tròn nhỏ và [[vuông góc]] với bán kính {{Math|''r''}} tại tiếp điểm, do đó {{Math|''d''}} và {{Math|''r''}} là các cạnh góc vuông của một [[tam giác vuông]] với cạnh huyền {{Math|''R''}} và diện tích hình vành khăn được tính theo công thức: |
||
: |
:<math>A = \pi\left(R^2 - r^2\right) = \pi d^2.</math> |
||
Cũng có thể áp dụng [[vi tích phân]] để tính diện tích bằng cách chia nhỏ hình vành khăn thành một số lượng hình vành khăn vô hạn với chiều rộng {{Math|''dρ''}} nhỏ đến vô cùng và diện tích {{Math|2π''ρ dρ''}}, sau đó giải [[tích phân]] từ {{Math|1=''ρ'' = ''r''}} đến {{Math|1=''ρ'' = ''R''}}:<ref>{{Chú thích sách|title=Cognitive Radio Oriented Wireless Networks: 12th International Conference, CROWNCOM 2017, Lisbon, Portugal, September 20-21, 2017, Proceedings|editor-first=Paulo|editor-last=Marques|editor-first2=Ayman|editor-last2=Radwan|editor-first3=Shahid|editor-last3=Mumtaz|editor-first4=Dominique|editor-last4=Noguet|editor-first5=Jonathan|editor-last5=Rodriguez|editor-first6=Michael|editor-last6=Gundlach|date=26 tháng 2 năm 2018|publisher=Springer|year=|isbn=3319762079|location=|pages=164|chapter=System Model|access-date=ngày 6 tháng 5 năm 2020|chapter-url=https://books.google.com/books?id=PPpNDwAAQBAJ&pg=PA164#v=onepage&q&f=false}}</ref> |
|||
: |
:<math>A = \int r^R\!\! 2\pi\rho\, d\rho = \pi\left(R^2 - r^2\right).</math> |
||
Diện tích hình quạt vành khăn với góc {{Math|''θ''}}, {{Math|''θ''}} đo bằng radian, được tính theo công thức: |
Diện tích hình quạt vành khăn với góc {{Math|''θ''}}, {{Math|''θ''}} đo bằng radian, được tính theo công thức: |
||
: <math> A = \frac{\theta}{2} \left(R^2 - r^2\right). </math> |
: <math> A = \frac{\theta}{2} \left(R^2 - r^2\right). </math> |
||
== Cấu trúc phức == |
== Cấu trúc phức == |
||
| Dòng 29: | Dòng 29: | ||
Nếu {{Math|''r''}} bằng {{Math|0}}, tập này được xem là '''đĩa thủng''' (punctured disk) có bán kính {{Math|''R''}}, tâm {{Math|''a''}}. |
Nếu {{Math|''r''}} bằng {{Math|0}}, tập này được xem là '''đĩa thủng''' (punctured disk) có bán kính {{Math|''R''}}, tâm {{Math|''a''}}. |
||
Là tập hợp con của [[Mặt phẳng (toán học)|mặt phẳng]] phức, hình vành khăn có thể được coi là một [[mặt Riemann]]. Cấu trúc phức của hình vành khăn chỉ phụ thuộc vào tỷ lệ {{Math|{{sfrac|''r''|''R''}}}}. Mỗi hình vành khăn {{Math|ann(''a''; ''r'', ''R'')}} có thể được ánh xạ [[Hàm chỉnh hình|chỉnh hình]] tới một hình vành khăn chuẩn tương ứng, dựa trên tâm cũ và với bán kính ngoài 1. |
Là tập hợp con của [[Mặt phẳng (toán học)|mặt phẳng]] phức, hình vành khăn có thể được coi là một [[mặt Riemann]].<ref>{{Chú thích sách|url=https://books.google.com/books?id=WpchAwAAQBAJ|title=A First Course in String Theory|last=Zwiebach|first=Barton|date=22 tháng 1 năm 2009|publisher=Cambridge University Press|year=|isbn=1139643916|edition=2|location=|pages=599|access-date=ngày 6 tháng 5 năm 2020}}</ref> Cấu trúc phức của hình vành khăn chỉ phụ thuộc vào tỷ lệ {{Math|{{sfrac|''r''|''R''}}}}. Mỗi hình vành khăn {{Math|ann(''a''; ''r'', ''R'')}} có thể được ánh xạ [[Hàm chỉnh hình|chỉnh hình]] tới một hình vành khăn chuẩn tương ứng, dựa trên tâm cũ và với bán kính ngoài 1. |
||
: <math>z \mapsto \frac{z - a}{R}.</math> |
: <math>z \mapsto \frac{z - a}{R}.</math> |
||
| Dòng 38: | Dòng 38: | ||
== Xem thêm == |
== Xem thêm == |
||
* [[Định lý hình vành khăn]] |
* [[Định lý hình vành khăn]] |
||
* [[Giải tích trực quan#Mô tả]], cung cấp cách biểu diễn trực quan diện tích hình vành khăn |
|||
* [[Vỏ cầu]] |
* [[Vỏ cầu]] |
||
* [[Hình xuyến]] |
* [[Hình xuyến]] |
||
| Dòng 46: | Dòng 44: | ||
== Tham khảo == |
== Tham khảo == |
||
{{Tham khảo}} |
|||
<references /> |
|||
== Liên kết ngoài == |
== Liên kết ngoài == |
||
* [http://www.mathopenref.com/annulus.html Định nghĩa và tính chất hình vành khăn] với hoạt hình tương tác |
* [http://www.mathopenref.com/annulus.html Định nghĩa và tính chất hình vành khăn] với hoạt hình tương tác |
||
* [http://www.mathopenref.com/annulusarea.html Diện tích hình vành khăn] với hoạt hình tương tác |
* [http://www.mathopenref.com/annulusarea.html Diện tích hình vành khăn] với hoạt hình tương tác |
||
Phiên bản lúc 03:24, ngày 6 tháng 5 năm 2020

Trong toán học, hình vành khăn (tiếng Anh: annulus, từ tiếng Latinh anulus / annulus, có nghĩa là "chiếc nhẫn nhỏ", số nhiều là anuli / annuli) là một vật hình nhẫn, phần mặt phẳng nằm giữa hai đường tròn đồng tâm.[2][3]
Những hình vành khăn mở tương đương tô pô với cả hình trụ mở S1 × (0,1) và mặt phẳng thủng (punctured plane).[4]
Diện tích
Diện tích hình vành khăn là hiệu của diện tích hình tròn lớn bán kính R với diện tích hình tròn nhỏ bán kính r:[5]
Diện tích hình vành khăn được xác định dựa vào độ dài của đoạn thẳng dài nhất trong hình, tức dây cung tiếp tuyến với đường tròn phía trong,[6] có độ dài 2d như hình minh họa. Có thể thể hiện phân tích này bằng định lý Pythagoras vì đoạn thẳng này tiếp tuyến với đường tròn nhỏ và vuông góc với bán kính r tại tiếp điểm, do đó d và r là các cạnh góc vuông của một tam giác vuông với cạnh huyền R và diện tích hình vành khăn được tính theo công thức:
Cũng có thể áp dụng vi tích phân để tính diện tích bằng cách chia nhỏ hình vành khăn thành một số lượng hình vành khăn vô hạn với chiều rộng dρ nhỏ đến vô cùng và diện tích 2πρ dρ, sau đó giải tích phân từ ρ = r đến ρ = R:[7]
Diện tích hình quạt vành khăn với góc θ, θ đo bằng radian, được tính theo công thức:
Cấu trúc phức
Trong giải tích phức, hình vành khăn ann(a; r, R) trong mặt phẳng phức là một tập mở được định nghĩa là:
Nếu r bằng 0, tập này được xem là đĩa thủng (punctured disk) có bán kính R, tâm a.
Là tập hợp con của mặt phẳng phức, hình vành khăn có thể được coi là một mặt Riemann.[8] Cấu trúc phức của hình vành khăn chỉ phụ thuộc vào tỷ lệ r/R. Mỗi hình vành khăn ann(a; r, R) có thể được ánh xạ chỉnh hình tới một hình vành khăn chuẩn tương ứng, dựa trên tâm cũ và với bán kính ngoài 1.
Bán kính trong lúc này là r/R < 1.
Định lý ba vòng tròn Hadamard là một phát biểu về giá trị tối đa mà hàm chỉnh hình có thể nhận được trong một hình vành khăn.
Xem thêm
Tham khảo
- ^ Haunsperger, Deanna; Kennedy, Stephen (2006). The Edge of the Universe: Celebrating Ten Years of Math Horizons. MAA. Truy cập ngày 29 tháng 4 năm 2020.
- ^ Gheverghese, Joseph George (28 tháng 7 năm 2016). Indian Mathematics: Engaging With The World From Ancient To Modern Times. World Scientific. tr. 239. ISBN 1786340631. Truy cập ngày 6 tháng 5 năm 2020.
- ^ Matthews, Bennie (21 tháng 6 năm 2019). “Circle”. Statics and Analytical Geometry. Scientific e-Resources. tr. 68. ISBN 1839473339. Truy cập ngày 6 tháng 5 năm 2020.
- ^ Hong, Weihu (15 tháng 12 năm 2016). “Surface of Cylinder”. Art of Mathematics. Dorrance Publishing. tr. 12. ISBN 1480930180. Truy cập ngày 6 tháng 5 năm 2020.
- ^ “Area of an Annulus”. Brightstorm. Bản gốc lưu trữ ngày 5 tháng 9 năm 2019. Truy cập ngày 6 tháng 5 năm 2020.
- ^ Coeurjolly, David; Sivignon, Isabelle; Tougne, Laure; Dupont, Florent biên tập (5 tháng 4 năm 2008). “The Limits of the Approach”. Discrete Geometry for Computer Imagery: 14th IAPR International Conference, DGCI 2008, Lyon, France, April 16-18, 2008, Proceedings. Springer. tr. 464. ISBN 3540791264. Truy cập ngày 6 tháng 5 năm 2020.
- ^ Marques, Paulo; Radwan, Ayman; Mumtaz, Shahid; Noguet, Dominique; Rodriguez, Jonathan; Gundlach, Michael biên tập (26 tháng 2 năm 2018). “System Model”. Cognitive Radio Oriented Wireless Networks: 12th International Conference, CROWNCOM 2017, Lisbon, Portugal, September 20-21, 2017, Proceedings. Springer. tr. 164. ISBN 3319762079. Truy cập ngày 6 tháng 5 năm 2020.
- ^ Zwiebach, Barton (22 tháng 1 năm 2009). A First Course in String Theory (ấn bản 2). Cambridge University Press. tr. 599. ISBN 1139643916. Truy cập ngày 6 tháng 5 năm 2020.
Liên kết ngoài
- Định nghĩa và tính chất hình vành khăn với hoạt hình tương tác
- Diện tích hình vành khăn với hoạt hình tương tác






