Diện tích

Diện tích là đại lượng biểu thị phạm vi của hình hoặc hình hai chiều hoặc lamina phẳng, trong mặt phẳng. Diện tích bề mặt là tương tự của diện tích trên bề mặt hai chiều của một vật thể ba chiều. Diện tích có thể được hiểu là lượng vật liệu có độ dày nhất định sẽ cần thiết để tạo kiểu cho mô hình hình dạng hoặc lượng sơn cần thiết để phủ lên bề mặt bằng một lớp sơn.[1] Nó là tương tự về mặt hai chiều đối với chiều dài của đường cong (khái niệm một chiều) hoặc thể tích của vật rắn (khái niệm ba chiều).
Diện tích của hình có thể được đo bằng cách so sánh hình với các hình vuông có kích thước cố định.[2] Trong Hệ thống đơn vị quốc tế (SI), đơn vị diện tích tiêu chuẩn là mét vuông (viết là m²), là diện tích của một hình vuông có cạnh dài một mét.[3] Một hình có diện tích ba mét vuông sẽ có cùng diện tích với ba hình vuông như vậy. Trong toán học, hình vuông đơn vị được xác định là có diện tích bằng một và diện tích của bất kỳ hình dạng hoặc bề mặt nào khác là một số thực không thứ nguyên.
Có một số công thức nổi tiếng cho các diện tích có hình dạng đơn giản như hình tam giác, hình chữ nhật và hình tròn. Sử dụng các công thức này, diện tích của bất kỳ đa giác nào đều có thể được tính toán bằng cách chia đa giác thành các hình tam giác.[4] Đối với các hình có ranh giới cong, tích phân thường được dùng để tính diện tích. Thật vậy, vấn đề xác định diện tích các hình phẳng là một động lực chính cho sự phát triển lịch sử của tích phân.[5]
Đối với một hình dạng rắn như hình cầu, hình nón hoặc hình trụ, diện tích bề mặt ranh giới của nó được gọi là diện tích bề mặt.[1][6][7] Các công thức cho các diện tích bề mặt của các hình dạng đơn giản đã được người Hy Lạp cổ đại tính toán, nhưng tính toán diện tích bề mặt của một hình dạng phức tạp hơn thường đòi hỏi tích phân đa biến.
Diện tích đóng một vai trò quan trọng trong toán học hiện đại. Ngoài tầm quan trọng rõ ràng của nó trong hình học và tính toán, diện tích có liên quan đến định nghĩa các yếu tố quyết định trong đại số tuyến tính, và là một tính chất cơ bản của các bề mặt trong hình học vi phân. Trong phân tích, diện tích của một tập hợp con của mặt phẳng được xác định bằng cách sử dụng thước đo Lebesgue,[8] mặc dù không phải mọi tập hợp con đều có thể đo được.[9] Nói chung, diện tích trong toán học cấp cao hơn được coi là một trường hợp đặc biệt về thể tích cho các vùng có hai chiều.[1]
Diện tích có thể được xác định thông qua việc sử dụng các tiên đề, xác định nó là một hàm của một tập hợp các hình mặt phẳng nhất định chiếu đến tập hợp các số thực. Nó có thể được chứng minh rằng một hàm như vậy là tồn tại.
Định nghĩa hình thức[sửa | sửa mã nguồn]
Một cách tiếp cận để xác định ý nghĩa của "diện tích" là thông qua các tiên đề. "Diện tích" có thể được định nghĩa là một hàm a từ tập hợp M gồm các hình phẳng đặc biệt (gọi là tập hợp có thể đo được) đến tập các số thực, thỏa mãn các tính chất sau:
- Với mọi S thuộc M thì a (S) ≥ 0.
- Nếu S và T nằm trong M thì S ∪ T và S ∩ T, và a (S ∪ T) = a (S) + a (T) - a (S ∩ T).
- Nếu S và T nằm trong M với S ⊆ T thì T - S thuộc M và a (T - S) = a (T) - a (S).
- Nếu một tập hợp S thuộc M và S đồng nhất với T thì T cũng thuộc M và a (S) = a (T.
- Mọi hình chữ nhật R đều nằm trong M. Nếu hình chữ nhật có chiều dài h và chiều rộng k thì a (R) = hk.
- Gọi Q là một tập hợp nằm giữa hai vùng bước S và T. Vùng bước được hình thành từ sự kết hợp hữu hạn của các hình chữ nhật liền kề nằm trên một cơ sở chung, tức là S ⊆ Q ⊆ T. Nếu tồn tại một số duy nhất c sao cho a (S) ≤ c ≤ a (T) đối với tất cả các vùng bước S và T như vậy, thì a (Q) = c.
Có thể chứng minh rằng một hàm diện tích như vậy thực sự tồn tại.[10]
Đơn vị[sửa | sửa mã nguồn]

Mọi đơn vị độ dài đều có một đơn vị diện tích tương ứng là diện tích hình vuông có độ dài cạnh bằng đơn vị độ dài đã cho. Do đó diện tích có thể được đo bằng mét vuông (m2), vuông cm (cm2), milimét vuông (mm2), kilômét vuông (km²),feet vuông (ft 2), yard vuông (yd 2), dặm vuông (mi2), v.v.[11] Về mặt đại số, các đơn vị này có thể được coi là bình phương của các đơn vị độ dài tương ứng.
Đơn vị diện tích SI là mét vuông, được coi là một đơn vị dẫn xuất SI.[3]
Chuyển đổi[sửa | sửa mã nguồn]

Tính diện tích của một hình vuông có chiều dài và chiều rộng là 1 mét sẽ là:
1 mét × 1 mét = 1 m²
và do đó, một hình chữ nhật có các cạnh khác nhau (giả sử chiều dài 3 mét và chiều rộng 2 mét) sẽ có diện tích tính bằng đơn vị hình vuông có thể được tính như sau:
3 mét × 2 mét = 6 m². Điều này tương đương với 6 triệu mm vuông. Các chuyển đổi hữu ích khác là:
- 1 km vuông = 1.000.000 mét vuông
- 1 mét vuông = 10.000 cm vuông = 1.000.000 mm vuông
- 1 cm vuông = 100 mm vuông.
Đơn vị không phải hệ mét[sửa | sửa mã nguồn]
Trong đơn vị không thuộc hệ mét, việc chuyển đổi giữa hai đơn vị vuông là bình phương của việc chuyển đổi giữa các đơn vị chiều dài tương ứng.
mối quan hệ giữa feet vuông và inch vuông là
1 foot vuông = 144 inch vuông,
trong đó 144 = 122 = 12 × 12. Tương tự:
- 1 yard vuông = 9 feet vuông
- 1 dặm vuông = 3.097.600 yard vuông = 27.878.400 feet vuông
Ngoài ra, các yếu tố chuyển đổi bao gồm:
- 1 inch vuông = 6.4516 cm vuông
- 1 foot vuông = 0.09290304 mét vuông
- 1 yard vuông = 0.83612736 mét vuông
- 1 dặm vuông = 2.589988110336 km vuông
Các đơn vị khác bao gồm các đơn vị mang tính lịch sử[sửa | sửa mã nguồn]
Có một số đơn vị phổ biến khác cho diện tích. A là đơn vị diện tích ban đầu trong hệ mét, với:
- 1 a = 100 mét vuông
Mặc dù đã không còn sử dụng, hecta vẫn thường được sử dụng để đo đất:[12]
- 1 hecta = 100 a = 10.000 mét vuông = 0,01 ki lô mét vuông
Mẫu Anh cũng thường được sử dụng để đo diện tích đất
- 1 mẫu Anh = 4,840 yard vuông = 43,560 feet vuông.
Một mẫu Anh là khoảng 40% của một hecta.
Trên quy mô nguyên tử, diện tích được đo bằng đơn vị barn:[13]
- 1 barn = 10 −28 mét vuông.
Barn được sử dụng phổ biến trong việc mô tả vùng tương tác mặt cắt ngang trong vật lý hạt nhân.[14]
Ở Ấn Độ,
- 20 dhurki = 1 dhur
- 20 dhur = 1 khatha
- 20 khata = 1 bigha
- 32 khata = 1 mẫu Anh
Lịch sử[sửa | sửa mã nguồn]
Diện tích hình tròn[sửa | sửa mã nguồn]
Vào thế kỷ thứ 5 trước Công nguyên, Hippocrates xứ Chios là người đầu tiên chỉ ra rằng diện tích của một cái đĩa (vùng được bao quanh bởi một vòng tròn) tỷ lệ với bình phương đường kính của nó, như một phần của việc cầu phương của ông,[15] nhưng không xác định được hằng số tỷ lệ. Eudoxus của Cnidus, cũng vào thế kỷ thứ 5 trước Công nguyên, cũng phát hiện ra rằng diện tích của một cái đĩa tròn tỷ lệ thuận với bình phương bán kính của nó.[16]
Sau đó, Quyển I của Cơ sở của Euclid đề cập đến sự bằng nhau về diện tích giữa các hình hai chiều. Nhà toán học Archimedes sử dụng các công cụ của Euclid để chứng minh rằng diện tích bên trong một vòng tròn là tương đương với của một tam giác vuông có đáy là chiều dài của chu vi của vòng tròn và có chiều cao tương đương với bán kính của vòng tròn, trong cuốn sách của ông Đo một hình tròn. (Chu vi là 2 πr, và diện tích của một tam giác bằng một nửa đáy nhân với chiều cao, mang lại diện tích πr 2 cho hình tròn.) Archimedes đã tính gần đúng giá trị của π (và do đó là diện tích của một hình tròn bán kính đơn vị) bằng phương pháp nhân đôi của mình, trong đó ông nội tiếp một tam giác đều trong một vòng tròn và ghi nhận diện tích của nó, sau đó nhân đôi số cạnh để tạo ra một hình lục giác đều., sau đó liên tục nhân đôi số cạnh khi diện tích của đa giác ngày càng gần với diện tích của hình tròn (và thực hiện tương tự với đa giác ngoại tiếp).
Nhà khoa học người Thụy Sĩ Johann Heinrich Lambert năm 1761 đã chứng minh rằng π, tỷ số giữa diện tích hình tròn với bán kính bình phương của nó, là số vô tỉ, nghĩa là nó không bằng thương số của hai số nguyên bất kỳ.[17] Năm 1794, nhà toán học người Pháp Adrien-Marie Legendre đã chứng minh rằng π2 là vô tỉ; điều này cũng chứng tỏ rằng π là vô tỉ.[18] Năm 1882, nhà toán học người Đức Ferdinand von Lindemann đã chứng minh rằng π là số siêu việt (không phải là nghiệm của bất kỳ phương trình đa thức nào với hệ số hữu tỉ), chứng minh này xác nhận một phỏng đoán của cả Legendre và Euler.[17] :p. 196
Diện tích tam giác[sửa | sửa mã nguồn]
Heron (hay Hero) của Alexandria đã tìm ra cái được gọi là công thức Heron cho diện tích tam giác tính theo các cạnh của nó, và một phép chứng minh có trong cuốn sách của ông, Metrica, được viết vào khoảng năm 60 CN. Có ý kiến cho rằng Archimedes đã biết công thức hơn hai thế kỷ trước đó,[19] và vì Metrica là tập hợp các kiến thức toán học có sẵn trong thế giới cổ đại, nên có thể công thức có trước tham chiếu được đưa ra trong công trình đó.[20]
Năm 499, Aryabhata, một nhà toán học - thiên văn học vĩ đại của thời đại cổ điển của toán học Ấn Độ và thiên văn học Ấn Độ, đã biểu thị diện tích của một tam giác bằng một nửa đáy nhân với chiều cao trong Aryabhatiya (phần 2.6).
Một công thức tương đương với Heron đã được người Trung Quốc tìm ra độc lập với người Hy Lạp. Nó được xuất bản vào năm 1247 trong Shushu Jiuzhang ("Cửu chương toán thuật"), tác phẩm của Qin Jiushao.
Diện tích tứ giác[sửa | sửa mã nguồn]
Trong thế kỷ thứ 7, Brahmagupta đã phát triển một công thức, bây giờ được gọi là công thức Brahmagupta, cho diện tích của một tứ giác nội tiếp (một tứ giác có các đỉnh nằm trên một vòng tròn) theo các cạnh của nó. Năm 1842, các nhà toán học người Đức Carl Anton Bretschneider và Karl Georg Christian von Staudt đã độc lập với nhau, cùng tìm ra một công thức, được gọi là công thức Bretschneider, cho diện tích của bất kỳ hình tứ giác nào.
Diện tích đa giác[sửa | sửa mã nguồn]
Sự phát triển của tọa độ Descartes do René Descartes xây dựng vào thế kỷ 17 cho phép phát triển công thức cho diện tích của bất kỳ đa giác nào có vị trí đỉnh đã biết của Gauss vào thế kỷ 19.
Diện tích được xác định bằng phép tính tích phân[sửa | sửa mã nguồn]
Sự phát triển của phép tính tích phân vào cuối thế kỷ 17 đã cung cấp các công cụ sau đó có thể được sử dụng để tính toán các diện tích phức tạp hơn, chẳng hạn như diện tích hình elip và diện tích bề mặt của các vật thể ba chiều cong khác nhau.
Công thức diện tích[sửa | sửa mã nguồn]
Đa giác[sửa | sửa mã nguồn]
Đối với một đa giác không tự cắt (đa giác đơn), tọa độ Descartes (i = 0, 1,..., n -1) của n đỉnh đã biết, diện tích được cho bởi công thức của người đóng móng:[21]
trong đó khi i = n -1, thì i +1 được biểu thị dưới dạng môđun n và do đó quy về 0.
Hình chữ nhật[sửa | sửa mã nguồn]

Công thức diện tích cơ bản nhất là công thức diện tích hình chữ nhật. Cho một hình chữ nhật có chiều dài l và chiều rộng w, công thức của diện tích là:[2][22]
A = lw.
Nghĩa là, diện tích của hình chữ nhật bằng chiều dài nhân với chiều rộng. Trong trường hợp đặc biệt, vì l = w trong trường hợp hình vuông, diện tích của hình vuông có độ dài cạnh s được cho bởi công thức:[1][2][23]
A = s2
Công thức cho diện tích hình chữ nhật trực tiếp dựa trên các tính chất cơ bản của diện tích, và đôi khi được coi là một định nghĩa hoặc tiên đề. Mặt khác, nếu hình học được phát triển trước số học, công thức này có thể được sử dụng để định nghĩa phép nhân các số thực.
Phương pháp tách hình, hình bình hành và hình tam giác[sửa | sửa mã nguồn]
Hầu hết các công thức đơn giản khác cho diện tích đều tuân theo phương pháp tách hình. Điều này bao gồm việc cắt một hình thành từng hình nhỏ, và việc tính diện tích hình đó sẽ là việc dùng phép cộng các diện tích các hình con.

Ví dụ, bất kỳ hình bình hành nào cũng có thể được chia nhỏ thành hình thang và tam giác vuông, như thể hiện trong hình bên trái. Nếu tam giác được di chuyển sang phía bên kia của hình thang, thì hình thu được là một hình chữ nhật. Theo đó diện tích của hình bình hành bằng diện tích của hình chữ nhật đó:[2]
A = bh (hình bình hành).
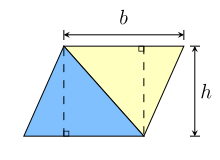
Tuy nhiên, cùng một hình bình hành cũng có thể được cắt theo một đường chéo thành hai tam giác tương đẳng, như trong hình bên phải. Như vậy diện tích của mỗi tam giác bằng một nửa diện tích của hình bình hành:[2]
(Tam giác).
Các phép chứng minh tương tự có thể được sử dụng để tìm công thức diện tích cho hình thang [24] cũng như các đa giác phức tạp hơn.[25]
Diện tích các hình cong[sửa | sửa mã nguồn]
Hình tròn[sửa | sửa mã nguồn]

Công thức tính diện tích hình tròn (được gọi đúng hơn là diện tích được bao bởi hình tròn hay diện tích đĩa) dựa trên một phương pháp tương tự. Cho một vòng tròn bán kính r nó có thể phân vùng các vòng tròn vào các lĩnh vực, như thể hiện trong hình bên phải. Mỗi cung có dạng hình tam giác gần đúng và các cung có thể được sắp xếp lại để tạo thành một hình bình hành gần đúng. Chiều cao của hình bình hành này là r, và chiều rộng bằng nửa chu vi của hình tròn, hay πr. Như vậy, tổng diện tích của hình tròn là πr2:[2]
A = πr2 (hình tròn).
Mặc dù việc phân tách hình tròn được sử dụng trong công thức này chỉ là gần đúng, nhưng sai số ngày càng nhỏ hơn khi vòng tròn được phân chia thành ngày càng nhiều cung. Giới hạn diện tích của các hình bình hành gần đúng là πr2, là diện tích của hình tròn.[26]
Lập luận này thực sự là một ứng dụng đơn giản của các ý tưởng của phép tính vi tích phân. Trong thời cổ đại, phương pháp cạn kiệt được sử dụng một cách tương tự để tìm diện tích hình tròn, và phương pháp này ngày nay được công nhận là tiền thân của phép tính tích phân. Sử dụng các phương pháp hiện đại, diện tích hình tròn có thể được tính bằng cách sử dụng một tích phân xác định:
Hình elip[sửa | sửa mã nguồn]
Công thức cho diện tích được bao bởi một hình elip có liên quan đến công thức của một hình tròn; đối với một hình elip với các bán trục chính và bán trục phụ x và y, với công thức là:[2]
Diện tích bề mặt[sửa | sửa mã nguồn]

Hầu hết các công thức cơ bản cho diện tích bề mặt có thể thu được bằng cách cắt các bề mặt và làm phẳng chúng. Ví dụ, nếu bề mặt bên của một hình trụ (hoặc bất kỳ hình lăng trụ nào) được cắt theo chiều dọc, bề mặt đó có thể được làm phẳng thành hình chữ nhật. Tương tự, nếu một vết cắt được thực hiện dọc theo mặt bên của hình nón, bề mặt bên có thể được làm phẳng thành một phần của hình tròn và diện tích kết quả có thể được tính ra.
Công thức cho diện tích bề mặt của một hình cầu khó tìm hơn: bởi vì một hình cầu có độ cong Gauss khác 0, nó không thể bị cán dẹt ra. Công thức về diện tích bề mặt của một hình cầu lần đầu tiên được Archimedes thu được trong tác phẩm Về hình cầu và hình trụ. Công thức là:[6]
- A = 4πr2 (hình cầu), với r là bán kính của hình cầu. Cũng giống như công thức về diện tích hình tròn, bất kỳ suy luận nào của công thức này đều sử dụng các phương pháp tương tự như tích phân.
Công thức chung[sửa | sửa mã nguồn]
Diện tích của các hình 2 chiều[sửa | sửa mã nguồn]

- Hình tam giác: (trong đó B là cạnh bất kỳ và h là khoảng cách từ đường thẳng mà B nằm đến đỉnh còn lại của tam giác). Có thể sử dụng công thức này nếu biết chiều cao h. Nếu biết độ dài của ba cạnh thì có thể sử dụng công thức Heron: trong đó a, b, c là các cạnh của tam giác và là một nửa chu vi của nó.[2] Nếu cho một góc và hai cạnh bên của nó, diện tích là trong đó C là góc đã cho và a và b là các cạnh của nó.[2] Nếu tam giác được vẽ đồ thị trên một mặt phẳng tọa độ, một ma trận có thể được sử dụng và được đơn giản hóa thành giá trị tuyệt đối của. Công thức này còn được gọi là công thức dây giày và là một cách dễ dàng để giải diện tích của một tam giác tọa độ bằng cách thay thế 3 điểm (x 1, y 1), (x 2, y 2) và (x 3, y 3). Công thức dây giày cũng có thể được sử dụng để tìm diện tích của các đa giác khác khi các đỉnh của chúng đã biết. Một cách tiếp cận khác cho tam giác tọa độ là sử dụng phép tính để tìm diện tích.
- Một đa giác đơn được xây dựng trên một lưới các điểm có khoảng cách bằng nhau (tức là các điểm có tọa độ nguyên) sao cho tất cả các đỉnh của đa giác là các điểm lưới:, với i là số điểm lưới bên trong đa giác và b là số điểm biên. Kết quả này được gọi là định lý Pick.[27]
Diện tích trong giải tích[sửa | sửa mã nguồn]


- Diện tích giữa đường cong có giá trị dương và trục hoành, được đo giữa hai giá trị a và b (b được định nghĩa là lớn hơn trong hai giá trị) trên trục hoành, được cho bởi tích phân từ a đến b của hàm đại diện cho đường cong:[1]
- Diện tích giữa đồ thị của hai hàm số bằng tích phân của một hàm số, f (x), trừ đi tích phân của hàm số kia, g (x):
- Diện tích bị giới hạn bởi một hàm r = r (θ) được biểu thị bằng tọa độ cực là:[1]
- Khu vực được bao quanh bởi một đường cong tham số với các điểm cuối được cho bởi tích phân đường:
- (xem định lý Green) hoặc thành phần z của
Các công thức thông dụng[sửa | sửa mã nguồn]
| Hình | Công thức | Biến số | Cách đọc |
|---|---|---|---|
| Hình chữ nhật | : Chiều dài, : Chiều rộng. | Diện tích bằng tích chiều dài 2 cạnh. | |
| Hình vuông | : Chiều dài cạnh hình vuông. | Diện tích bằng bình phương chiều dài 1 cạnh. | |
| Hình bình hành | : Chiều dài 1 cạnh, : chiều cao tương ứng với a. | Diện tích bằng 1 cạnh nhân với chiều cao tương ứng với cạnh đó. | |
| Hình thoi | : Chiều dài 2 đường chéo. | Diện tích bằng 1 nửa tích độ dài 2 đường chéo. | |
| Tam giác | : cạnh đáy, : chiều cao. | Diện tích bằng 1 nửa tích chiều dài 1 cạnh với đường cao tương ứng với nó. | |
| Hình tròn | : bán kính. | Diện tích bằng số pi nhân với bình phương bán kính | |
| Hình e-líp | và độ dài nửa trục thực và nửa trục ảo. | ||
| Mặt cầu | , hoặc | : bán kính, : đường kính hình cầu. | Diện tích bằng số Pi nhân với bình phương chiều dài đường kính. |
| Hình thang | và : các cạnh đáy, : chiều cao. | Diện tích bằng trung bình cộng 2 đáy nhân với chiều cao. | |
| Hình trụ tròn | : bán kính, : chiều cao. | ||
| Diện tích xung quanh của hình trụ | : bán kính, : chiều cao | ||
| Mặt nón | : bán kính, độ dài đường sinh (slant height). | ||
| Diện tích xung quanh của hình nón | : bán kính, độ dài đường sinh (slant height). | ||
| Hình quạt | : bán kính, số đo góc ở tâm,l là độ dài cung. |
Xem thêm[sửa | sửa mã nguồn]
Tham khảo[sửa | sửa mã nguồn]
- ^ a b c d e f Weisstein, Eric W. “Area”. Wolfram MathWorld. Bản gốc lưu trữ ngày 5 tháng 5 năm 2012. Truy cập ngày 3 tháng 7 năm 2012.
- ^ a b c d e f g h i “Area Formulas”. Math.com. Bản gốc lưu trữ ngày 2 tháng 7 năm 2012. Truy cập ngày 2 tháng 7 năm 2012.
- ^ a b “Resolution 12 of the 11th meeting of the CGPM (1960)”. Bureau International des Poids et Mesures. Bản gốc lưu trữ ngày 28 tháng 7 năm 2012. Truy cập ngày 15 tháng 7 năm 2012.
- ^ Mark de Berg; Marc van Kreveld; Mark Overmars; Otfried Schwarzkopf (2000). “Chapter 3: Polygon Triangulation”. Computational Geometry (ấn bản 2). Springer-Verlag. tr. 45–61. ISBN 978-3-540-65620-3.
- ^ Boyer, Carl B. (1959). A History of the Calculus and Its Conceptual Development. Dover. ISBN 978-0-486-60509-8.
- ^ a b Weisstein, Eric W. “Surface Area”. Wolfram MathWorld. Bản gốc lưu trữ ngày 23 tháng 6 năm 2012. Truy cập ngày 3 tháng 7 năm 2012.
- ^ Foundation, CK-12. “Surface Area”. CK-12 Foundation (bằng tiếng Anh). Truy cập ngày 9 tháng 10 năm 2018.
- ^ Walter Rudin (1966). Real and Complex Analysis, McGraw-Hill, ISBN 0-07-100276-6.
- ^ Gerald Folland (1999). Real Analysis: modern techniques and their applications, John Wiley & Sons, Inc., p. 20, ISBN 0-471-31716-0
- ^ Moise, Edwin (1963). Elementary Geometry from an Advanced Standpoint. Addison-Wesley Pub. Co. Truy cập ngày 15 tháng 7 năm 2012.
- ^ Bureau international des poids et mesures (2006). “The International System of Units (SI)” (PDF). 8th ed. Bản gốc (PDF) lưu trữ ngày 5 tháng 11 năm 2013. Truy cập ngày 13 tháng 2 năm 2008. Chú thích journal cần
|journal=(trợ giúp) Chapter 5. - ^ Bureau international des poids et mesures (2006). “The International System of Units (SI)” (PDF). 8th ed. Bản gốc (PDF) lưu trữ ngày 5 tháng 11 năm 2013. Truy cập ngày 13 tháng 2 năm 2008. Chú thích journal cần
|journal=(trợ giúp) Chapter 5. - ^ Bureau international des poids et mesures (2006). “The International System of Units (SI)” (PDF). 8th ed. Bản gốc (PDF) lưu trữ ngày 5 tháng 11 năm 2013. Truy cập ngày 13 tháng 2 năm 2008. Chú thích journal cần
|journal=(trợ giúp) Chapter 5. - ^ Bureau international des poids et mesures (2006). “The International System of Units (SI)” (PDF). 8th ed. Bản gốc (PDF) lưu trữ ngày 5 tháng 11 năm 2013. Truy cập ngày 13 tháng 2 năm 2008. Chú thích journal cần
|journal=(trợ giúp) Chapter 5. - ^ , ISBN 978-0-486-43231-1
|title=trống hay bị thiếu (trợ giúp) - ^ Stewart, James (2003). Single variable calculus early transcendentals (ấn bản 5). Toronto ON: Brook/Cole. tr. 3. ISBN 978-0-534-39330-4.
However, by indirect reasoning, Eudoxus (fifth century B.C.) used exhaustion to prove the familiar formula for the area of a circle:
- ^ a b Arndt, Jörg; Haene l, Christoph (2006). Pi Unleashed. Springer-Verlag. ISBN 978-3-540-66572-4. Truy cập ngày 5 tháng 6 năm 2013. English translation by Catriona and David Lischka.
- ^ , ISBN 978-0-03-029558-4
|title=trống hay bị thiếu (trợ giúp) - ^ Heath, Thomas L. (1921). A History of Greek Mathematics (Vol II). Oxford University Press. tr. 321–323.
- ^ Weisstein, Eric W., "Diện tích" từ MathWorld.
- ^ Bourke, Paul (tháng 7 năm 1988). “Calculating The Area And Centroid Of A Polygon” (PDF). Bản gốc (PDF) lưu trữ ngày 16 tháng 9 năm 2012. Truy cập ngày 6 tháng 2 năm 2013.
- ^ “Area of Parallelogram/Rectangle”. ProofWiki.org. Bản gốc lưu trữ ngày 20 tháng 6 năm 2015. Truy cập ngày 29 tháng 5 năm 2016.
- ^ “Area of Square”. ProofWiki.org. Bản gốc lưu trữ ngày 4 tháng 11 năm 2017. Truy cập ngày 29 tháng 5 năm 2016.
- ^ Problem Solving Through Recreational Mathematics, 2012, ISBN 978-0-486-13174-0
- ^ Calculus for Scientists and Engineers: An Analytical Approach, 2002, ISBN 978-0-8493-1319-6
- ^ Braden, Bart (tháng 9 năm 1986). “The Surveyor's Area Formula” (PDF). The College Mathematics Journal. 17 (4): 326–337. doi:10.2307/2686282. JSTOR 2686282. Bản gốc (PDF) lưu trữ ngày 27 tháng 6 năm 2012. Truy cập ngày 15 tháng 7 năm 2012.
- ^ Trainin, J. (tháng 11 năm 2007). “An elementary proof of Pick's theorem”. Mathematical Gazette. 91 (522): 536–540.












































