Tứ giác
| Hình tứ giác | |
|---|---|
 Một số dạng của hình tứ giác | |
| Số cạnh và đỉnh | 4 |
| Ký hiệu Schläfli | {4} (đối với hình vuông) |
| Diện tích | Nhiều phương pháp |
| Góc ngoài (độ) | 90° (đối với hình vuông và hình chữ nhật) |
| Hình học | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||
| Nhà hình học | ||||||||||
|
theo tên
|
||||||||||
|
theo giai đoạn
|
||||||||||

Trong hình học phẳng Euclid, một tứ giác là một đa giác gồm 4 cạnh và 4 đỉnh, trong đó không có bất kỳ 2 đoạn thẳng nào cùng nằm trên một đường thẳng. Tứ giác đơn có thể lồi hay lõm. Tứ giác có các đỉnh , , và đôi khi được ký hiệu là .[1]
Tổng các góc trong của tứ giác đơn bằng 360 độ, tức là: + + + = .
Tứ giác đơn[sửa | sửa mã nguồn]
Bất kỳ tứ giác không có 2 cạnh không kề nhau nào cắt nhau là một tứ giác đơn.
Tứ giác lồi[sửa | sửa mã nguồn]
Trong một tứ giác lồi, tất cả các góc trong đều nhỏ hơn 180° và hai đường chéo đều nằm trong tứ giác. Một khái niệm phổ biến hơn là tứ giác luôn nằm gọn trên một nửa mặt phẳng có bờ chứa bất kỳ cạnh nào của nó thì đó là tứ giác lồi.
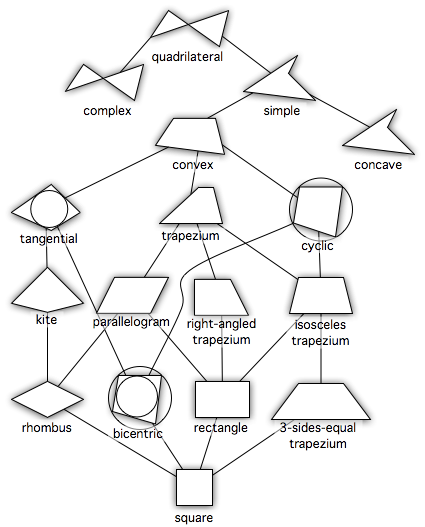
- Tứ giác không đều: không có cặp cạnh nào song song với nhau. Tứ giác không đều thường được dùng để đại diện cho tứ giác lồi nói chung (không phải là tứ giác đặc biệt).
- Hình thang: có ít nhất 2 cạnh đối song song và bao gồm cả hình bình hành.
- Hình thang cân: có 2 cạnh đối song song và các góc kề với một cạnh đáy bằng nhau. Các định nghĩa khác là một tứ giác với một trục đối xứng chia đôi hình thành hai mặt đối nhau, hoặc hình thang với 2 đường chéo bằng nhau.
- Hình bình hành: có 2 cặp cạnh đối song song một tứ giác với hai cặp song song. Điều kiện tương đương là các cạnh đối bằng nhau, góc đối thì bằng nhau, đường chéo cắt nhau tại trung điểm mỗi đường. Hình bình hành bao gồm hình thoi (bao gồm cả các hình chữ nhật chúng ta gọi là hình vuông) và hình gần thoi (bao gồm cả những hình chữ nhật chúng ta gọi là hình thuôn). Nói cách khác, các hình bình hành bao gồm tất cả các hình thoi và tất cả các hình gần thoi, và do đó cũng bao gồm tất cả các hình chữ nhật.
- Hình thoi: là hình có 4 cạnh bằng nhau; điều kiện tương đương là 2 đường chéo vuông góc tại trung điểm mỗi đường. Hình thoi là một trường hợp đặc biệt của cả hình diều và hình bình hành.
- Hình gần thoi: các cạnh kề không bằng nhau và không có góc vuông. Hình gần thoi thường được dùng để đại diện cho hình bình hành nói chung (không phải hình thoi hay hình chữ nhật).
- Hình chữ nhật: tất cả các góc đều là góc vuông. Một điều kiện tương đương là 2 đường chéo cắt nhau và chiều dài bằng nhau. Hình chữ nhật bao gồm hình vuông và hình thuôn.
- Hình vuông: có bốn cạnh bằng nhau và 4 góc bằng nhau (góc vuông). Các điều kiện tương đương là các cạnh đối song song (hình vuông là một hình bình hành), các đường chéo vuông góc tại trung điểm mỗi đoạn và có cùng chiều dài. Một tứ giác là một hình vuông khi và chỉ khi nó là một hình thoi (4 cạnh bằng nhau) và một hình chữ nhật (bốn góc bằng nhau).
- Hình thuôn: là một thuật ngữ đôi khi được sử dụng để biểu thị một hình chữ nhật có các cạnh kề không bằng nhau (tức là hình chữ nhật không phải là hình vuông).[2]
- Hình diều: có hai cạnh kề bằng nhau và 2 cạnh còn lại bằng nhau; đồng nghĩa với 1 cặp góc đối bằng nhau và các đường chéo vuông góc, đối xứng qua một đường chéo. Hình diều bao gồm cả hình thoi.

- Hình thang vuông: có một góc vuông.
- Tứ giác nội tiếp: có 4 đỉnh nằm trên đường tròn ngoại tiếp.
- Tứ giác ngoại tiếp: tứ giác có 4 cạnh tiếp xúc với đường tròn nội tiếp.
- Hình diều vuông: hình diều có hai góc vuông đối nhau. Nó là một dạng của tứ giác nội tiếp.
Tứ giác lõm[sửa | sửa mã nguồn]
Trong một hình tứ giác lõm (tứ giác không lồi), một góc trong có số đo lớn hơn 180° và một trong hai đường chéo nằm bên ngoài tứ giác.
Tứ giác kép[sửa | sửa mã nguồn]
Một tứ giác có 2 cạnh cắt nhau được gọi là một tứ giác kép.
Phân loại[sửa | sửa mã nguồn]
Sự phân loại các tứ giác được minh họa trong biểu đồ dưới đây. Các dạng ở mức thấp hơn là trường hợp đặc biệt của các dạng nằm ở mức trên.
Xem thêm[sửa | sửa mã nguồn]
Tham khảo[sửa | sửa mã nguồn]
- ^ “Quadrilaterals - Square, Rectangle, Rhombus, Trapezoid, Parallelogram”. Mathsisfun.com. Truy cập ngày 2 tháng 9 năm 2020.
- ^ “The Rectangles Calculator”. Truy cập ngày 25 tháng 10 năm 2023.
Liên kết ngoài[sửa | sửa mã nguồn]
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Tứ giác. |