Hình thoi
Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin. |

Hình thoi trong hình học Euclide là tứ giác có bốn cạnh bằng nhau. Đây là hình bình hành có hai cạnh kề bằng nhau hay hình bình hành có hai đường chéo vuông góc với nhau.
Định nghĩa
Hình thoi là tứ giác có bốn cạnh bằng nhau.
Tính chất
Trong hình thoi:
- Các góc đối nhau bằng nhau.
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Hai đường chéo là các đường phân giác của các góc của hình thoi.
- Hình thoi có tất cả tính chất của hình bình hành.
Diện tích
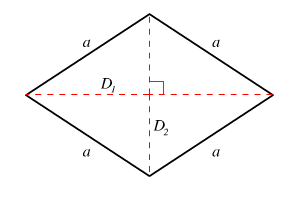
Diện tích của hình thoi bằng một nửa tích độ dài của hai đường chéo:
Chu vi
Chu vi của hình thoi bằng độ dài một cạnh nhân với 4:
Dấu hiệu nhận biết
Hình tứ giác đặc biệt
- Tứ giác có bốn cạnh bằng nhau là hình thoi.
- Tứ giác có 2 đường chéo là đường trung trực của nhau là hình thoi.
- Tứ giác có 2 đường chéo là đường phân giác của cả bốn góc là hình thoi.
Hình bình hành đặc biệt
Hình thoi là một dạng đặc biệt của một hình bình hành vì nó có đầy đủ tính chất của hình bình hành và còn có một số tính chất khác:
- Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
- Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Tham khảo
Liên kết ngoài
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Hình thoi. |


