Tứ giác nội tiếp

Trong hình học phẳng, một tứ giác nội tiếp là một tứ giác mà cả bốn đỉnh đều nằm trên một đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp, và các đỉnh của tứ giác được gọi là đồng viên. Tâm và bán kính đường tròn lần lượt được gọi là tâm đường tròn ngoại tiếp và bán kính đường tròn ngoại tiếp. Thông thường tứ giác nội tiếp là tứ giác lồi, nhưng cũng tồn tại các tứ giác nội tiếp lõm. Các công thức trong bài viết sẽ chỉ áp dụng cho tứ giác lồi.
Một tam giác bất kì luôn có một đường tròn ngoại tiếp, nhưng không phải tứ giác nào cũng là tứ giác nội tiếp. Một ví dụ cho một tứ giác không nội tiếp là một hình bình hành không là hình chữ nhật.
Trường hợp đặc biệt về một tứ giác nội tiếp[sửa | sửa mã nguồn]
Mọi hình vuông, hình chữ nhật, hình thang cân đều nội tiếp.
Một tứ giác lưỡng tâm là một tứ giác nội tiếp mà cũng ngoại tiếp một đường tròn.
Đặc điểm, tính chất, dấu hiệu nhận biết[sửa | sửa mã nguồn]
Dấu hiệu nhận biết[sửa | sửa mã nguồn]
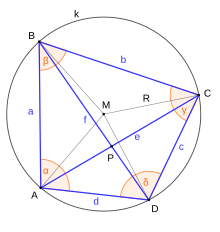
Một tứ giác lồi là tứ giác nội tiếp khi và chỉ khi bốn đường trung trực của bốn cạnh đồng quy tại một điểm. Điểm đồng quy này chính là tâm đường tròn ngoại tiếp.[1]
Tứ giác ABCD nội tiếp khi và chỉ khi hai góc đối bù nhau, tức là[1]
- Ở đây
Định lý trên được nêu trong bộ Cơ bản của Euclid.[2] Từ đó ta có khẳng định sau: Một tứ giác nội tiếp khi và chỉ khi một góc trong bằng góc ngoài đối diện góc đó.
Một trong các dấu hiệu nhận biết quan trọng khác để tứ giác ABCD nội tiếp là tứ giác có hai góc bằng nhau cùng nhìn một cạnh của tứ giác đó.[3] Ví dụ như:
Định lý Ptoleme cũng chỉ ra rằng một tứ giác nội tiếp khi và chỉ khi tích hai đường chéo bằng tổng của tích hai cặp cạnh đối, tức là:[4]
Nếu hai đường thẳng lần lượt chứa hai đoạn thẳng AC và BD, cắt nhau tại P, thì A, B, C, D cùng thuộc đường tròn khi và chỉ khi:[5]
Giao điểm P có thể nằm trong hoặc nằm ngoài đường tròn. Trong trường hợp nằm trong, tứ giác lồi nội tiếp là ABCD, còn trong trường hợp còn lại, tứ giác nội tiếp là ABDC.
Một dấu hiệu nhận biết khác là tứ giác ABCD nội tiếp khi và chỉ khi:[6]
Đặc điểm, tính chất[sửa | sửa mã nguồn]
Tâm đường tròn ngoại tiếp của tứ giác nội tiếp là giao điểm của các đường trung trực của các cạnh.
Nếu tứ giác nội tiếp có 2 góc đối diện là góc vuông thì tâm đường tròn ngoại tiếp là trung điểm của đường chéo nối liền 2 đỉnh kia.
Nếu tứ giác nội tiếp có 2 góc vuông cùng nhìn 1 cạnh thì tâm đường tròn ngoại tiếp là trung điểm của cạnh mà 2 góc cùng nhìn.
Diện tích[sửa | sửa mã nguồn]
Diện tích S của tứ giác nội tiếp với các cạnh a, b, c, d được cho bởi công thức Brahmagupta:[4]:p.24
trong đó p là nửa chu vi tứ giác hay p = 1/2(a + b + c + d). Đây là hệ quả của công thức Brahmagupta cho một tứ giác bất kỳ. Nếu d = 0, tứ giác sẽ trở thành một tam giác và công thức trên được rút gọn về công thức Heron.
Tứ giác nội tiếp có diện tích lớn nhất trong các tứ giác có các cạnh tương ứng bằng nhau. Đây cũng là một hệ quả được rút ra từ công thức Brahmagupta.[7]
Với bốn số đo cạnh khác nhau, mỗi số nhỏ hơn tổng ba số còn lại, là độ dài các cạnh của ba tứ giác nội tiếp khác nhau,[8] mà theo công thức Brahmagupta, tất cả đều có cùng diện tích. Trong đó, với bốn cạnh a, b, c, d, cạnh a có thể là cạnh đối của một trong ba cạnh còn lại b, c, d.
Diện tích của tứ giác nội tiếp với các cạnh a, b, c, d, cạnh a đối cạnh c, cạnh b đối cạnh d và góc trong B tạo bởi hai cạnh a và b; cũng có thể biểu diễn dưới dạng:[4]:p.25
hay[4]:p.26
với θ là góc tạo bởi hai đường chéo của tứ giác. Nếu góc trong A bất kỳ không là góc vuông, diện tích của tứ giác là:[4]:p.26
trong đó a và d là hai cạnh kề góc A.
Một công thức khác đó là[9]:p.83
trong đó R là bán kính đường tròn nội tiếp. Từ đó có kết quả:[10]
tại đó dấu bằng xảy ra khi tứ giác là hình vuông.
Đường chéo tứ giác[sửa | sửa mã nguồn]
Trong một tứ giác nội tiếp có bốn đỉnh A, B, C, D và cạnh a = AB, b = BC, c = CD, d = DA, độ dài đường chéo p = AC và q = BD có thể được cho bởi công thức[4]:p.25,[11][12]:p. 84
- và
Tích hai đường chéo được xác định bởi định lý Ptoleme:
Cũng theo định lý Ptolemy thứ hai thì[4]:p.25,[11]
Với tổng hai đường chéo ta có bất đẳng thức:[13]
dấu bằng xảy ra khi và chỉ khi 2 đường chéo có độ dài bằng nhau, bất đẳng thức này có thể được chứng minh bằng bất đẳng thức AM-GM.
Từ bất đẳng thức trên ta có kết quả:[14]
Với mọi tứ giác lồi, hai đường chéo cắt nhau chia tứ giác thành bốn tam giác. Trong tứ giác nội tiếp, cặp hai tam giác đối nhau qua giao hai đường chéo đồng dạng với nhau.
Nếu M và N lần lượt là trung điểm hai đường chéo AC và BD thì[15]
trong đó E và F lần lượt là giao điểm hai cặp cạnh đối của tứ giác.
Nếu tứ giác ABCD nội tiếp có AC cắt BD tại E, thì[16]
Với một bộ bốn cạnh là bốn cạnh một tứ giác nội tiếp, có thể thay đổi thứ tự các cạnh theo một trật tự bất kỳ. Khi đó có thể tạo ra một trong hai tứ giác nội tiếp khác nhau và khác tứ giác ban đầu. Cả ba tứ giác đều có diện tích bằng nhau do tính chất công thức Brahmagupta, đều nội tiếp cùng một đường tròn, và bất cứ hai trong ba tứ giác đều có một cặp hai đường chéo bằng nhau.[12]:p. 84
Công thức các góc và liên hệ giữa các góc trong tứ giác[sửa | sửa mã nguồn]
Với một tứ giác nội tiếp có bốn cạnh a, b, c, d, nửa chu vi s, và góc A nằm giũa hai cạnh a và d, ta có các công thức lượng giác sau đây:[17]
Góc θ tạo bởi hai đường chéo được xác định bởi:[4]:p.26
Nếu đường thẳng chứa 2 cạnh a và c cắt nhau tao thành góc φ, thì:[4]:p.31
Công thức Parameshvara về bán kính đường tròn ngoại tiếp[sửa | sửa mã nguồn]
Một tứ giác nội tiếp có các cạnh a, b, c, d và nửa chu vi s; có độ dài bán kính đường tròn ngoại tiếp xác định bởi:[11][18]
Công thức được tìm ra vào thế kỷ XV bởi nhà toán học Ấn Độ Vatasseri Parameshvara.
Sử dụng công thức Brahmagupta, công thức Parameshvara có thể được phát biểu lại là:
trong đó K là diện tích tứ giác nội tiếp.
Các tính chất, định lý khác[sửa | sửa mã nguồn]

- Trong một tứ giác nội tiếp ABCD, các tâm đường tròn nội tiếp M1, M2, M3, M4 (xem Hình 3) của các tam giác DAB, ABC, BCD, và CDA là 4 đỉnh của một hình chữ nhật. Đây là phát biểu của định lý Nhật Bản về tứ giác nội tiếp. Ngoài ra, các trực tâm của bốn tam giác trên là đỉnh của một tứ giác nội tiếp đồng dạng với tứ giác ABCD, và các trọng tâm của bốn tam giác này cũng tạọ nên một tứ giác nội tiếp.[3]
- Trong một tứ giác nội tiếp ABCD với tâm ngoại tiếp O, gọi P là giao điểm của AC và BD. Ta có số đo góc APB là trung bình cộng của số đo hai góc AOB và COD. Đây là một kết quả trực tiếp suy ra từ đinh lý góc trong và định lý góc ngoài[19].
- Không tồn tại một tứ giác nội tiếp có diện tích và số đo bốn cạnh khác nhau đều là số hữu tỉ.[20].
- Nếu hai cặp cạnh đối của tứ giác cắt nhau tại E và F, thì tia phân giác của hai góc trong có đỉnh E và F là vuông góc với nhau.[8]
Tứ giác Brahmagupta[sửa | sửa mã nguồn]
Một tứ giác Brahmagupta là một tứ giác nội tiếp với các cạnh, các đường chéo và diện tích là số nguyên. Tất cả các tứ giác Brahmagupta với các cạnh a, b, c, d, đường chéo e, f, diện tích K, và bán kính đường tròn ngoại tiếp R có thể được thu được bằng cách quy đồng các mẫu số từ các biểu thức sau liên quan đến các số hữu tỉ t, u, v:
Trường hợp hai đường chéo vuông góc[sửa | sửa mã nguồn]
Chu vi và diện tích
Đối với một tứ giác nội tiếp có 2 đường chéo vuông góc, giả sử giao điểm của đường chéo chia một đường chéo thành các đoạn có độ dài p1 và p2 và chia đường chéo khác thành các đoạn có độ dài q1 và q2 thì: (đẳng thức đầu tiên là Mệnh đề thứ 11 trong cuốn "Book of Lemmas" (tạm dịch: Cuốn sách về bổ đề) của Archimedes)
trong đó D là đường kính của đường tròn ngoại tiếp tứ giác. Điều này đúng bởi vì đường chéo là các dây vuông góc của một vòng tròn. Các phương trình này thể hiện rằng bán kính đường tròn ngoại tiếp R có thể được biểu diễn bằng
hoặc, ở dạng của các cạnh của tứ giác, như
Tương đương:
Do đó, theo định lý tứ giác của Euler, bán kính đường tròng ngoại tiếp có thể được biểu diễn theo các đường chéo p và q, và khoảng cách x giữa trung điểm các đường chéo:
Một công thức cho diện tích K của một tứ giác nội tiếp có hai đường chéo vuông góc ở dạng độ dài 4 cạnh thu được trực tiếp khi kết hợp định lý Ptoleme và công thức tính diện tích của một tứ giác nội tiếp có hai đường chéo vuông góc. Kết quả là
Tính chất khác[sửa | sửa mã nguồn]
Trong một tứ giác nội tiếp có hai đường chéo vuông góc, tâm đường tròn nội tiếp trùng với điểm mà các đường chéo giao nhau.[cần dẫn nguồn]
- Định lý Brahmagupta cho rằng đối với một tứ giác nội tiếp có hai đường chéo vuông góc, đường vuông góc từ bất kỳ cạnh nào qua giao điểm của các đường chéo chia đôi cạnh phía đối diện.[cần dẫn nguồn]
- Nếu một tứ giác có hai đường chéo vuông góc cũng nội tiếp, khoảng cách từ tâm đường tròn ngoại tiếp đến bất kỳ cạnh nào bằng một nửa chiều dài của phía đối diện.[cần dẫn nguồn]
- Trong một tứ giác có hai đường chéo vuông góc, khoảng cách giữa trung điểm của các đường chéo bằng khoảng cách giữa tâm đừong tròn ngoại tiếp và giao điểm hai đường chéo.[cần dẫn nguồn]
Ngược lại: Nếu tứ giác nội tiếp có tổng bình phương hai cạnh đối này bằng tổng bình phương hai cạnh đối kia tam giác đó thì hai đường chéo của nó vuông góc với nhau. (hay chứng minh định lí 4 điểm[cần dẫn nguồn])
Hình cầu ngoại tiếp tứ giác[sửa | sửa mã nguồn]
Một tứ giác nằm trên hình cầu được tạo bởi các giao điểm của các đường tròn lớn hơn là một tứ giác nội tiếp khi và chỉ khi tổng của các góc đối diện bằng nhau, tức là α + γ = β + δ cho các góc liên tiếp α, β, γ, δ của tứ giác. Một hướng của định lý này đã được chứng minh bởi I.A.Lexell năm 1786. Lexell cho thấy rằng trong một hình tứ giác nằm trên hình cầu nội tiếp một đường tròn nhỏ của một khối cầu, tổng các góc đối nhau đều bằng nhau, và trong tứ giác ngoại tiếp, tổng các cạnh đối diện nhau đều bằng nhau. Định lý đầu tiên của các định lý này là sự tương đồng hình cầu của một định lý phẳng và định lý thứ hai là kết hợp của nó, nghĩa là kết quả của việc trao đổi các vòng tròn lớn và cực của chúng. Kiper và cộng sự đã chứng minh được định lí đảo: Nếu tổng của các cạnh đối diện bằng nhau trong một tứ giác nằm trên hình cầu, thì tồn tại một đường tròn nội tiếp của tứ giác này.
Xem thêm[sửa | sửa mã nguồn]
Chú thích[sửa | sửa mã nguồn]
- ^ a b Usiskin, Zalman; Griffin, Jennifer; Witonsky, David; Willmore, Edwin (2008), “10. Cyclic quadrilaterals”, The Classification of Quadrilaterals: A Study of Definition, Research in mathematics education, IAP, tr. 63–65, ISBN 978-1-59311-695-8
- ^ Joyce, D. E. (tháng 6 năm 1997), “Book 3, Proposition 22”, Euclid's Elements, Clark University
- ^ a b Andreescu, Titu; Enescu, Bogdan (2004), “2.3 Cyclic quads”, Mathematical Olympiad Treasures, Springer, tr. 44–46, 50, ISBN 978-0-8176-4305-8, MR 2025063
- ^ a b c d e f g h i Durell, C. V.; Robson, A. (2003) [1930], Advanced Trigonometry, Courier Dover, ISBN 978-0-486-43229-8
- ^ Bradley, Christopher J. (2007), The Algebra of Geometry: Cartesian, Areal and Projective Co-Ordinates, Highperception, tr. 179, ISBN 1906338000, OCLC 213434422
- ^ Hajja, Mowaffaq (2008), “A condition for a circumscriptible quadrilateral to be cyclic” (PDF), Forum Geometricorum, 8: 103–6
- ^ Peter, Thomas (tháng 9 năm 2003), “Maximizing the area of a quadrilateral”, The College Mathematics Journal, 34 (4): 315–6, JSTOR 3595770
- ^ a b Coxeter, Harold Scott MacDonald; Greitzer, Samuel L. (1967), “3.2 Cyclic Quadrangles; Brahmagupta's formula”, Geometry Revisited, Mathematical Association of America, tr. 57, 60, ISBN 978-0-88385-619-2
- ^ Prasolov, Viktor, Problems in plane and solid geometry: v.1 Plane Geometry (PDF), Bản gốc (PDF) lưu trữ ngày 21 tháng 9 năm 2018, truy cập ngày 4 tháng 12 năm 2017
- ^ Alsina, Claudi; Nelsen, Roger (2009), “4.3 Cyclic, tangential, and bicentric quadrilaterals”, When Less is More: Visualizing Basic Inequalities, Mathematical Association of America, tr. 64, ISBN 978-0-88385-342-9
- ^ a b c Alsina, Claudi; Nelsen, Roger B. (2007), “On the diagonals of a cyclic quadrilateral” (PDF), Forum Geometricorum, 7: 147–9
- ^ a b Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).
- ^ Inequalities proposed in Crux Mathematicorum, 2007, Problem 2975, p. 123
- ^ Inequalities proposed in "Crux Mathematicorum", [1].
- ^ “ABCD is a cyclic quadrilateral. Let M, N be midpoints of diagonals AC, BD respectively...”. Art of Problem Solving. 2010.[liên kết hỏng]
- ^ A. Bogomolny, An Identity in (Cyclic) Quadrilaterals, Interactive Mathematics Miscellany and Puzzles, [2], Accessed ngày 18 tháng 3 năm 2014.
- ^ Siddons, A. W.; Hughes, R. T. (1929), Trigonometry, Cambridge University Press, tr. 202, OCLC 429528983
- ^ Hoehn, Larry (tháng 3 năm 2000), “Circumradius of a cyclic quadrilateral”, Mathematical Gazette, 84 (499): 69–70, JSTOR 3621477
- ^ "Cyclic quadrilateral" trên wikipedia: https://en.wikipedia.org/wiki/Cyclic_quadrilateral
- ^ Buchholz, R. H.; MacDougall, J. A. (1999), “Heron quadrilaterals with sides in arithmetic or geometric progression”, Bulletin of the Australian Mathematical Society, 59 (2): 263–9, doi:10.1017/S0004972700032883, MR 1680787
Tham khảo[sửa | sửa mã nguồn]
- Derivation of Formula for the Area of Cyclic Quadrilateral
- Incenters in Cyclic Quadrilateral từ cut-the-knot
- Four Concurrent Lines in a Cyclic Quadrilateral từ cut-the-knot
- Weisstein, Eric W., "Cyclic quadrilateral" từ MathWorld.
- Euler centre and maltitudes of cyclic quadrilateral từ Dynamic Geometry Sketches, interactive dynamic geometry sketch.




























![{\displaystyle a=[t(u+v)+(1-uv)][u+v-t(1-uv)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9cd163fbbbaa9656bd5676b09a171e5cbbb85e5b)





![{\displaystyle K=uv[2t(1-uv)-(u+v)(1-t^{2})][2(u+v)t+(1-uv)(1-t^{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/093f0b615f9b1a926b92deb5fb486cc82281c53d)






