Hàm số
| Hàm số | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x ↦ f (x) | |||||||||||||||||||||||||||||||||
| Ví dụ theo miền xác định và miền giá trị | |||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| Loại/tính chất | |||||||||||||||||||||||||||||||||
| Hằng · Đồng nhất · Tuyến tính · Đa thức · Hữu tỉ · Đại số · Giải tích · Trơn · Liên tục · Đo được · Đơn ánh · Toàn ánh · Song ánh | |||||||||||||||||||||||||||||||||
| Xây dựng | |||||||||||||||||||||||||||||||||
| Thu hẹp · Hợp · λ · Ngược | |||||||||||||||||||||||||||||||||
| Tổng quát | |||||||||||||||||||||||||||||||||
| Bộ phận · Nhiều giá trị · Ẩn | |||||||||||||||||||||||||||||||||
Trong toán học, một hàm số[note 1] hay gọi ngắn là hàm (Tiếng Anh: function) là một loại ánh xạ giữa hai tập hợp số liên kết mọi phần tử của tập số đầu tiên với đúng một phần tử của tập số thứ hai. Ví dụ điển hình là các hàm từ số nguyên sang số nguyên hoặc từ số thực sang số thực.
Các hàm số ban đầu là sự lý tưởng hóa cách một đại lượng thay đổi phụ thuộc vào một đại lượng khác. Ví dụ, vị trí của một hành tinh là một hàm số của thời gian. Về mặt lịch sử, khái niệm này được xây dựng dựa trên phép tính vi tích phân vào cuối thế kỷ 17, và cho đến thế kỷ 19, các hàm được coi là khả vi (nghĩa là chúng có mức độ mịn cao). Khái niệm hàm số được chính thức hóa vào cuối thế kỷ 19 dưới dạng lý thuyết tập hợp, và điều này đã mở rộng đáng kể các lĩnh vực ứng dụng của khái niệm này.
Một hàm số là một quá trình hoặc một mối quan hệ mà liên kết mỗi phần tử x của một tập hợp X, được gọi là miền xác định của hàm số, đến một phần tử y duy nhất của một tập hợp Y (có thể là cùng một tập hợp như X), và gọi là tập hợp đích của hàm số này. Hàm số thường được ký hiệu bằng các chữ cái như f, g và h.[1]
Nếu hàm được gọi là f, quan hệ này được ký hiệu là y = f (x) (đọc là " f của x "), trong đó phần tử x là đối số hoặc đầu vào của hàm và y là giá trị của hàm, đầu ra hoặc ảnh của x theo f .[2] Ký hiệu được sử dụng để biểu diễn đầu vào là biến của hàm (ví dụ: f là hàm của biến x).[3]
Một hàm số được biểu diễn duy nhất bởi tập hợp tất cả các cặp số (x, f (x)), được gọi là đồ thị của hàm số. [note 2][4] Khi miền và miền là tập hợp các số thực, mỗi cặp như vậy có thể được coi là tọa độ Descartes của một điểm trong mặt phẳng. Tập hợp các điểm này được gọi là đồ thị của hàm số; nó là một phương tiện phổ biến để minh họa một hàm số.



Các hàm số được sử dụng rộng rãi trong khoa học và trong hầu hết các lĩnh vực toán học. Người ta đã nói rằng các hàm là "đối tượng trung tâm của nghiên cứu" trong hầu hết các lĩnh vực toán học.[5]
Khái niệm[sửa | sửa mã nguồn]
Nói một cách trực quan, hàm là một quá trình liên kết từng phần tử của tập hợp số X với một phần tử của tập hợp số Y.
Về mặt hình thức, một hàm f từ tập X đến tập Y được xác định bởi tập G gồm các cặp có thứ tự (x, y) sao cho x ∈ X, y ∈ Y, và mọi phần tử của X là thành phần đầu tiên của đúng một cặp có thứ tự ghép đôi trong G [6] [note 3] Nói cách khác, với mọi x trong X, có đúng một phần tử y sao cho cặp có thứ tự (x, y) thuộc tập các cặp xác định hàm f . Tập hợp G được gọi là đồ thị của hàm số. Về mặt hình thức, nó có thể được xác định với hàm số trên, nhưng điều này che giấu cách giải thích thông thường về một chức năng như một quá trình. Do đó, trong cách sử dụng thông thường, hàm số thường được phân biệt với đồ thị của nó.
Trong định nghĩa về hàm số, X và Y tương ứng được gọi là tập/miền xác định và tập đích/ miền giá trị của hàm f [7] Nếu (x, y) thuộc tập xác định f, thì y là ảnh của x thông qua f, hoặc giá trị của f được áp dụng cho đối số x . Đặc biệt, trong ngữ cảnh của các con số, người ta cũng nói rằng y là giá trị của f đối với giá trị x của biến của nó, hay ngắn gọn hơn, y là giá trị của f của x, được ký hiệu là y = f(x) .
Hai hàm f và g là bằng nhau, nếu miền và tập hợp miền xác định của chúng giống nhau và giá trị đầu ra của chúng giống nhau trên toàn miền xác định đó. Chính thức hơn, f = g nếu f(x) = g(x) với mọi x ∈ X, trong đó f:X → Y và g:X → Y [8] [9] [note 4]
Miền xác định và miền giá trị không phải lúc nào cũng được cung cấp rõ ràng khi một hàm được xác định và, nếu không có một số tính toán (có thể khó), người ta có thể chỉ biết rằng miền được chứa trong một tập hợp lớn hơn. Thông thường, điều này xảy ra trong giải tích toán học, trong đó "một hàm từ X tới Y " thường đề cập đến một hàm có thể có một tập con thích hợp[note 5] của X là miền xác định. Ví dụ, một "hàm từ giá trị thực đến giá trị thực" có thể tham chiếu đến một hàm có giá trị thực của một biến thực. Tuy nhiên, một "hàm từ số thực đến số thực" không có nghĩa là miền của hàm là toàn bộ tập các số thực, mà chỉ có nghĩa miền là tập các số thực có chứa khoảng mở không rỗng. Khi đó một hàm như vậy được gọi là hàm một phần. Ví dụ: nếu f là một hàm có các số thực là miền xác định và miền giá trị, thì một hàm ánh xạ giá trị x với giá trị là một hàm g từ miền số thực đến miền số thực, có miền xác định là tập các số thực x, sao cho f(x) ≠ 0 .
Phạm vi của một hàm là tập hợp các ảnh của tất cả các phần tử trong miền.[10][11][12] Tuy nhiên, phạm vi đôi khi được sử dụng như một từ đồng nghĩa của miền giá trị,[12][13] thường sử dụng trong các sách cũ.
Định nghĩa dùng quan hệ[sửa | sửa mã nguồn]
Bất kỳ tập con nào của tích Descartes gồm hai tập hợp và xác định một quan hệ hai ngôi giữa hai tập hợp này. Rõ ràng là một quan hệ tùy ý có thể chứa các cặp đôi vi phạm các điều kiện cần thiết cho một hàm số đã cho ở trên.
Một quan hệ hai ngôi là có tính hàm số (còn được gọi là duy nhất bên phải) nếu
Một quan hệ nhị phân là có tính nối tiếp (còn được gọi là tổng bên trái) nếu
Một hàm một phần là một quan hệ hai ngôi mà có tính hàm số..
Một hàm số là một quan hệ hai ngôi có tính hàm số và nối tiếp.
Các thuộc tính khác nhau của hàm số và thành phần hàm số có thể được định dạng lại bằng ngôn ngữ của các quan hệ. Ví dụ, một hàm số là đơn ánh nếu quan hệ ngược là có tính hàm số, trong đó quan hệ ngược được định nghĩa là [14]
Cách cho hàm số[sửa | sửa mã nguồn]
Hàm số có thể được cho bằng bảng hoặc bằng biểu đồ hoặc bằng 1 biểu thức hoặc nhiều biểu thức trên từng khoảng, đoạn, nửa khoảng.
Ví dụ: X = {1,2,3,4,5}, Y = {5,6,7,8,9,10}.
Hàm được cho bảng sau:
| x | 1 | 2 | 3 | 4 | 5 |
| y | 5 | 6 | 7 | 8 | 9 |
Các hàm cho bằng biểu thức như , , ...
Lưu ý: Trong chương trình môn Toán ở bậc Trung học phổ thông của Việt Nam (chỉ đề cập đến Hàm số biến số thực) quy ước rằng:
- Khi không nói rõ thêm, miền xác định (tập xác định) của hàm số cho bằng biểu thức y = f(x) là tập hợp tất cả các giá trị của x làm cho f(x) có nghĩa.
- Ví dụ: Hàm số có miền xác định là hay
- Hàm số có miền xác định là
- Miền giá trị của hàm số y = f(x) là tập hợp tất cả các giá trị có thể có của , nghĩa là .
- Ví dụ: Miền giá trị của hàm số là .
- Nếu X,Y thì hàm số được gọi là hàm số thực.
- Ví dụ: Hàm lượng giác ,hàm mũ ,...
- Nếu X,Y thì hàm số được gọi là hàm số biến số phức.
- Ví dụ: Hàm dao động ;
- Nếu X thì hàm số được gọi là hàm số số học.
- Ví dụ: Hàm Euler biểu diễn số các số tự nhiên không vượt quá n và nguyên tố cùng nhau với n, hàm Sigma biểu diễn tổng tất cả các ước của số tự nhiên n...
Các dạng của hàm số[sửa | sửa mã nguồn]
Đơn ánh, song ánh, toàn ánh[sửa | sửa mã nguồn]
Như trên đã đề cập, hàm số là một trường hợp ánh xạ, nên người ta cũng miêu tả hàm số dưới 3 dạng là đơn ánh, toàn ánh và song ánh.
Đơn ánh[sửa | sửa mã nguồn]
Một hàm số là đơn ánh khi nó áp dụng lên 2 đối số khác nhau luôn cho 2 giá trị khác nhau.
Một cách chặt chẽ, hàm f, xác định trên X và nhận giá trị trong Y, là đơn ánh nếu như nó thỏa mãn điều kiện với mọi x1 và x2 thuộc X và nếu x1 ≠ x2 thì f(x1) ≠ f(x2).
Nghĩa là, hàm số f là đơn ánh khi và chỉ khi:
Với đồ thị hàm số y = f(x) trong hệ tọa độ Đề các, mọi đường thẳng vuông góc với trục đối số Ox sẽ chỉ cắt đường cong đồ thị tại nhiều nhất là một điểm
Toàn ánh[sửa | sửa mã nguồn]
Hàm số f được gọi là toàn ánh nếu như với mọi số y thuộc Y ta luôn tìm được ít nhất một số x thuộc X sao cho f(x) = y. Theo cách gọi của ánh xạ thì điều kiện này có nghĩa là mỗi phần tử y thuộc Y đều là ảnh của ít nhất một tạo ảnh x thuộc X qua ánh xạ f.
Nghĩa là, hàm số f là toàn ánh khi và chỉ khi:
- cũng tức là
Đồ thị hàm cắt đường thẳng
Song ánh[sửa | sửa mã nguồn]
Trong toán học, song ánh, hoặc hàm song ánh, là một hàm số f từ tập X vào tập Y thỏa mãn tính chất, đối với mỗi y thuộc Y, có duy nhất một x thuộc X sao cho f(x) = y.
Nói cách khác, f là một song ánh nếu và chỉ nếu nó là tương ứng một-một giữa hai tập hợp; tức là nó vừa là đơn ánh và vừa là toàn ánh.
Ví dụ, xét hàm fxác định trên tập hợp số nguyên vào, được định nghĩa f(x) = x + 1. Ví dụ khác, đối với mỗi cặp số thực (x,y) hàm f xác định bởi f(x,y) = (x + y, x − y) là một song ánh
Hàm song ánh đôi khi còn gọi là hoán vị.
Tập hợp tất cả các song ánh từ tập X vào tập Y được ký hiệu là X ↔ Y. Thông thường tập các hoán vị của tập X được ký hiệu là X!.
Song ánh đóng nhiều vai trò quan trọng trong toán học, như nó dùng để định nghĩa đẳng cấu (và những khái niệm liên quan như phép đồng phôi và vi phôi), nhóm hoán vị, ánh xạ xạ ảnh, và nhiều định nghĩa khác
Minh hoạ[sửa | sửa mã nguồn]
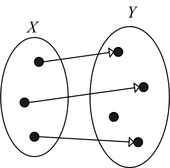 |  | 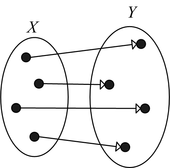 | ||
| Đơn ánh nhưng không phải toàn ánh | Toàn ánh nhưng không phải đơn ánh | Song ánh |
Hàm hợp và hàm ngược[sửa | sửa mã nguồn]
Hàm hợp[sửa | sửa mã nguồn]
Cho các hàm số:
trong đó X, Y, Z là các tập hợp số nói chung. Hàm hợp của f1 và f2 là hàm số:
được định nghĩa bởi:
Có thể ký hiệu hàm hợp là:
Ví dụ, hàm số f(x) = sin (x2+1) là hàm số hợp f2(f1(x)), trong đó f2(y) = sin(y), f1(x) = (x2 +1).
Việc nhận biết một hàm số là hàm hợp của các hàm khác, trong nhiều trường hợp có thể khiến các tính toán giải tích (đạo hàm, vi phân, tích phân) trở nên đơn giản hơn.
Hàm ngược[sửa | sửa mã nguồn]
Cho hàm số song ánh:
trong đó X, Y là tập hợp số nói chung.Khi đó mỗi phần tử y = f(x) với y nằm trong Y đều là ảnh của một và chỉ một phần tử x trong X. Như vậy, có thể đặt tương ứng mỗi phần tử y trong Y với một phần tử x trong X. Phép tương ứng đó đã xác định một hàm số, ánh xạ từ Y sang X, hàm số này được gọi là hàm số ngược của hàm số f và được ký hiệu là:
Nếu f−1(x) tồn tại ta nói hàm số f(x) là khả nghịch. Có thể nói tính chất song ánh là điều kiện cần và đủ để hàm f(x) khả nghịch, tức là nếu f(x) là song ánh thì ta luôn tìm được hàm ngược f−1(x) và ngược lại.
Đồ thị của hàm số[sửa | sửa mã nguồn]
Thông thường thì hàm số được xác định bằng một biểu thức tổng quát y = f(x) nào đó, ví dụ như y = x2 - 5. Tuy nhiên cũng có những hàm đặc biệt mà quy tắc cho tương ứng x với y của nó không theo bất kỳ một quy luật nào để có thể diễn đạt bằng một biểu thức toán học. Trong trường hợp này ta có thể lập bảng cho các giá trị đối số x và các giá trị hàm số y tương ứng với chúng. Ngoài ra hàm số còn có thể được xác định một cách triệt để bằng đồ thị của nó.
Đối với hàm số một biến số thực (có miền xác định thực), đồ thị hàm số được định nghĩa như sau:
- Đồ thị của hàm số y = f(x) là tập hợp các điểm trên mặt phẳng R2 có tọa độ [x, f(x)].
Ký hiệu đồ thị hàm số theo định nghĩa trên là:
Các tính chất của hàm số[sửa | sửa mã nguồn]
Tính đơn điệu[sửa | sửa mã nguồn]
Giả sử hàm số y= f(x) xác định trên K. Ta nói:
- Hàm số y= f(x) đồng biến (tăng) trên K nếu với mọi cặp , thuộc K mà nhỏ hơn thì nhỏ hơn , tức là:
- Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi cặp , thuộc K mà nhỏ hơn thì lớn hơn , tức là:
Tính chẵn lẻ[sửa | sửa mã nguồn]
Điều kiện để một hàm số chẵn hoặc lẻ[sửa | sửa mã nguồn]
Cho hàm số y=f(x) xác định trên D
- Điều kiện tiên quyết để hàm số có tính chẵn lẻ là tập xác định của hàm số phải đối xứng qua điểm 0, tức là
- Để hàm số được xem là chẵn cần thêm điều kiện f(-x) = f(x)
- Để hàm số được xem là lẻ cần thêm điều kiện f(-x) = -f(x)
- Nếu thiếu điều kiện 1 hoặc cả hai điều kiện 2 và 3 thì xem như hàm số không có tính chẵn lẻ.
Đồ thị của hàm số chẵn và hàm số lẻ[sửa | sửa mã nguồn]
Trong mặt phẳng tọa độ Descartes:
- Đồ thị của mọi hàm số chẵn đều nhận trục Oy làm trục đối xứng.
- Đồ thị của mọi hàm số lẻ đều nhận gốc tọa độ làm tâm đối xứng.
Tham khảo[sửa | sửa mã nguồn]
- ^ “Compendium of Mathematical Symbols”. Math Vault (bằng tiếng Anh). 1 tháng 3 năm 2020. Truy cập ngày 17 tháng 8 năm 2020.
- ^ MacLane, Saunders; Birkhoff, Garrett (1967). Algebra . New York: Macmillan. Truy cập ngày 31 tháng 1 năm 2021.
- ^ “What is a Function”. www.mathsisfun.com. Truy cập ngày 17 tháng 8 năm 2020.
- ^ “function | Definition, Types, Examples, & Facts”. Encyclopedia Britannica (bằng tiếng Anh). Truy cập ngày 17 tháng 8 năm 2020.
- ^ Spivak 2008, tr. 39.
- ^ Hamilton, A. G. (1982). Numbers, sets, and axioms: the apparatus of mathematics. https://archive.org/details/numberssetsaxiom0000hami/page/83 83: Cambridge University Press. ISBN 978-0-521-24509-8.
function is a relation.
Quản lý CS1: địa điểm (liên kết) - ^ Weisstein, Eric W. “Function”. mathworld.wolfram.com (bằng tiếng Anh). Truy cập ngày 17 tháng 8 năm 2020.
- ^ Apostol 1981, tr. 35.
- ^ Kaplan 1972, tr. 25.
- ^ Bản mẫu:Taalman Kohn Calculus
- ^ Bản mẫu:Trench Intro Real Analysis
- ^ a b Bản mẫu:Thomson Bruckner Bruckner Elementary Real Analysis
- ^ Bản mẫu:Princeton Companion to Mathematics
- ^ Gunther Schmidt(2011) Relational Mathematics, Encyclopedia of Mathematics and its Applications, vol. 132, sect 5.1 Functions, pp. 49–60, Cambridge University Press ISBN 978-0-521-76268-7 CUP blurb for Relational Mathematics
Chú thích[sửa | sửa mã nguồn]
- ^ The words map, mapping, transformation, correspondence, and operator are often used synonymously. Halmos 1970.
- ^ This definition of "graph" refers to a set of pairs of objects. Graphs, in the sense of diagrams, are most applicable to functions from the real numbers to themselves. All functions can be described by sets of pairs but it may not be practical to construct a diagram for functions between other sets (such as sets of matrices).
- ^ The sets X, Y are parts of data defining a function; i.e., a function is a set of ordered pairs with , together with the sets X, Y, such that for each , there is a unique with in the set.
- ^ This follows from the axiom of extensionality, which says two sets are the same if and only if they have the same members. Some authors drop codomain from a definition of a function, and in that definition, the notion of equality has to be handled with care; see, for example, “When do two functions become equal?”. Stack Exchange. ngày 19 tháng 8 năm 2015.
- ^ called the domain of definition by some authors, notably computer science

















![{\displaystyle [1;3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3c912bda6f9de8cc164c067f38dc8221a48950f)



![{\displaystyle [0;2.5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3b6c5dfb5574a6ef8c7bda23518eb0b49c634b6)






























