Số vô tỉ
Trong toán học, các số vô tỷ (Tiếng Anh: irrational number) là tất cả các số thực không phải là số hữu tỷ, nghĩa là không thể biểu diễn dưới dạng tỉ số của hai số nguyên. Khi tỷ lệ độ dài của hai đoạn thẳng là một số vô tỉ, các đoạn thẳng này cũng được mô tả là không thể đo lường được, có nghĩa là chúng không chia sẻ "thước đo" chung, nghĩa là không có độ dài ("số đo") chung, dù là ngắn đến đâu, mà có thể được sử dụng để thể hiện độ dài của cả hai đoạn thẳng đã cho dưới dạng bội số nguyên của cùng một đoạn thẳng đơn vị chung.
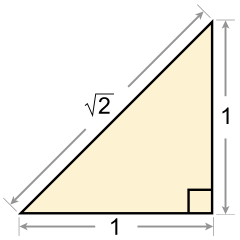
Các ví dụ về số vô tỉ là tỷ lệ π của chu vi của vòng tròn với đường kính của nó, số Euler e, tỷ lệ vàng φ, và căn bậc hai của hai;[1][2][3] trong thực tế, tất cả các căn bậc hai của số tự nhiên, trừ căn bậc hai của các số chính phương, đều là các số vô tỉ.
Có thể chỉ ra rằng các số vô tỉ, khi được biểu thị trong một hệ thống cơ số (ví dụ như số thập phân hoặc với bất kỳ cơ số tự nhiên nào khác), là các chuỗi không chấm dứt, cũng không lặp lại, nghĩa là không chứa một chuỗi các chữ số, mà có sự lặp lại ở phần đuôi của cách biểu diễn số. Ví dụ: biểu diễn thập phân của số π bắt đầu bằng 3.14159, nhưng không có số chữ số hữu hạn nào có thể đại diện chính xác cho số π, và cũng không có sự lặp lại. Việc chứng minh cho thấy việc mở rộng thập phân của số hữu tỉ phải chấm dứt hoặc lặp lại khác với chứng minh rằng việc mở rộng thập phân chấm dứt hoặc lặp lại phải là một số hữu tỉ, và mặc dù sơ cấp và không dài, cả hai chứng minh đều không đơn giản. Các nhà toán học thường không coi việc thể hiện thập phân là "chấm dứt hoặc lặp lại" là định nghĩa của khái niệm số hữu tỉ.
Số vô tỉ cũng có thể được xử lý thông qua các liên phân số không kết thúc.
Như một hệ quả của chứng minh của Cantor rằng các số thực là không thể đếm được và các số hữu tỷ có thể đếm được, theo đó hầu như tất cả các số thực là các số vô tỉ.[4]
Lịch sử[sửa | sửa mã nguồn]

Hy Lạp cổ đại[sửa | sửa mã nguồn]
Bằng chứng đầu tiên cho thấy về sự tồn tại của các số vô tỉ thường được quy cho một người theo trường phái Pythagore (cũng có thể là Hippasus của Metapontum),[5] người có thể đã phát hiện ra chúng trong khi xác định các cạnh của ngôi sao năm cánh.[6] Phương pháp Pythagore hiện tại đã tuyên bố rằng phải có một số đơn vị đủ nhỏ, không thể phân chia, có thể vừa khít với một trong những độ dài này cũng như các chiều dài khác. Tuy nhiên, Hippasus, vào thế kỷ thứ 5 TCN, đã có thể suy luận rằng trên thực tế không có đơn vị đo lường chung nào, và việc khẳng định sự tồn tại như vậy trên thực tế là một mâu thuẫn. Ông đã làm điều này bằng cách chứng minh rằng nếu cạnh huyền của tam giác vuông cân thực sự có tỷ lệ đo được khi so với cạnh góc vuông, thì một trong những độ dài được đo theo đơn vị đo đó phải là số lẻ và số chẵn, điều này là không thể. Lý luận của ông là như sau:
- Giả sử chúng ta có một tam giác vuông cân với các số nguyên cạnh a, b và c. Tỷ lệ của cạnh huyền với một chân được biểu thị bằng c:b.
- Giả sử a, b và c là các số hạng nhỏ nhất có thể (nghĩa là chúng không có ước số chung).
- Theo định lý Pythagoras: c2 = a2 + b2 = b2 + b2 = 2b2. (Vì tam giác là cân, nên a = b).
- Vì c2 = 2b2, c2 chia hết cho 2 và do đó chẵn.
- Vì c2 là chẵn nên c phải chẵn.
- Vì c là chẵn nên chia c cho 2 có thương là số nguyên. Đặt y là số nguyên này (c = 2y).
- Bình phương cả hai vế của c = 2y thu được c2 = (2y)2 hoặc c2 = 4y2.
- Thay 4y2 cho c2 theo phương trình thứ nhất (c2 = 2b2) cho kết quả 4y2 = 2b2.
- Chia cho 2 thu được 2y2 = b2.
- Vì y là một số nguyên và 2y2 = b2, b2 phải chia hết cho 2 và do đó là số chẵn.
- Vì b2 là chẵn nên b phải chẵn.
- Chúng ta vừa chỉ ra rằng cả b và c phải là số chẵn. Do đó chúng có ước số chung là 2. Tuy nhiên, điều này mâu thuẫn với giả định rằng chúng không có ước số chung. Mâu thuẫn này chứng minh rằng cả c và b không thể là số nguyên và do đó, có sự tồn tại của một số không thể biểu thị bằng tỷ lệ của hai số nguyên.[7]
Các nhà toán học Hy Lạp đã gọi tỉ lệ này là các số không thể đo lường được, hoặc không thể diễn tả được. Tuy nhiên, Hippasus không được ca ngợi vì những nỗ lực của mình: theo một truyền thuyết, ông đã khám phá ra điều này khi đang ở ngoài biển và sau đó bị các nhà toán học cùng trường phái Pythagore của ông ném ra khỏi tàu vì đã tạo ra một yếu tố trong vũ trụ mà phản đối lại học thuyết, rằng tất cả các hiện tượng trong vũ trụ có thể được tối giản thành các số nguyên và tỉ lệ của chúng." [8] Một truyền thuyết nói rằng Hippasus chỉ đơn thuần là phải đi lưu vong vì chứng minh này. Dù hậu quả của Hippasus là gì, khám phá của ông đã đặt ra một vấn đề rất nghiêm trọng đối với toán học Pythagore, vì nó phá vỡ giả định rằng số lượng và hình học không thể tách rời – một nền tảng của lý thuyết này.
Việc phát hiện ra các tỉ lệ không thể tối giản/đo được cho thấy một vấn đề khác mà người Hy Lạp phải đối mặt: mối quan hệ của sự rời rạc với sự liên tục. Điều này đã được Zeno of Elea đưa ra ánh sáng, người đã đặt câu hỏi về quan niệm rằng số lượng là rời rạc và bao gồm một số lượng đơn vị hữu hạn có kích thước nhất định. Các quan niệm của Hy Lạp trong quá khứ cho rằng chúng nhất thiết phải có, vì toàn bộ các số đại diện cho các đối tượng rời rạc và tỉ lệ tương xứng biểu thị mối quan hệ giữa hai bộ sưu tập các đối tượng rời rạc,[9] nhưng Zeno thấy rằng "trong thực tế số lượng không phải là tổng/tập hợp của các đơn vị; Đây là lý do tại sao các tỉ lệ không thể giải quyết được [số lượng] xuất hiện. Số lượng, nói cách khác là liên tục." Điều này có nghĩa là, trái với quan niệm phổ biến về thời gian, không thể có một đơn vị không thể chia nhỏ nhất, mà chúng ta có thể dùng nó như đơn vị đo cho bất kỳ số lượng nào. Trong thực tế, các phân chia số lượng này nhất thiết phải là vô hạn. Ví dụ, hãy xem xét một đoạn thẳng: đoạn thẳng này có thể được chia làm đôi, một nửa chia thành một nửa nữa, một nửa mới chia này tiếp tục chia thành một nửa nữa, và như vậy. Quá trình này có thể tiếp tục đến vô tận, vì luôn có một nửa khác bị chia đôi. Càng nhiều lần đoạn thẳng được chia đôi, đơn vị đo càng gần bằng 0, nhưng nó không bao giờ đạt đến số 0 chính xác. Đây chỉ là những gì Zeno tìm cách chứng minh. Ông đã tìm cách chứng minh điều này bằng cách xây dựng bốn nghịch lý, điều này chứng minh những mâu thuẫn vốn có trong tư tưởng toán học thời đó. Mặc dù nghịch lý của Zeno đã chứng minh chính xác những thiếu sót của các quan niệm toán học khi đó, chúng không được coi là bằng chứng của sự thay thế. Trong suy nghĩ của người Hy Lạp, việc bác bỏ tính hợp lệ của một quan điểm không nhất thiết phải chứng minh tính hợp lệ của một quan điểm khác, và do đó phải tiến hành điều tra thêm.
Bước tiếp theo được Eudoxus của Cnidus thực hiện, người đã chính thức nêu ra một lý thuyết mới về tỷ lệ có tính đến số lượng tương xứng cũng như không thể so sánh được. Trung tâm của ý tưởng của ông là sự phân biệt giữa cường độ và số lượng. Một cường độ... không phải là một con số mà là viết tắt của các thực thể như đoạn thẳng, góc, diện tích, khối lượng và thời gian có thể thay đổi, như chúng ta sẽ nói, liên tục. Độ lớn trái ngược với các con số, nhảy từ giá trị này sang giá trị khác, chẳng hạn từ 4 đến 5."[10] Các số được tạo thành từ một số đơn vị nhỏ nhất, không thể chia, trong khi cường độ có thể giảm vô hạn. Do không có giá trị định lượng nào được gán cho độ lớn, Eudoxus sau đó có thể tính cả hai tỷ lệ tương xứng và không thể đo được bằng cách xác định tỉ lệ theo độ lớn của nó và tỷ lệ là một đẳng thức giữa hai tỉ lệ. Bằng cách lấy các giá trị định lượng (số) ra khỏi phương trình, ông tránh được cái bẫy phải biểu thị một số vô tỷ dưới dạng số. Lý thuyết của Euxoxus cho phép các nhà toán học Hy Lạp đạt được tiến bộ to lớn về hình học bằng cách cung cấp nền tảng logic cần thiết cho các tỷ lệ vô tỷ.[11] Tính không tương thích này được giải quyết trong Tác phẩm Cơ bản của Euclid, Quyển X, Proposition 9.
Do sự phân biệt giữa số lượng và cường độ, hình học trở thành phương pháp duy nhất có thể biểu diễn được các tỉ lệ là số vô tỉ. Bởi vì các nền tảng số học trước đây vẫn chưa tương thích với khái niệm về số vô tỉ, trọng tâm của toán học Hy Lạp đã ngừng tập trung nghiên cứu các khái niệm về số như đại số và hầu như chỉ tập trung vào hình học. Trong thực tế, trong nhiều trường hợp, các khái niệm đại số đã được cải tổ thành các thuật ngữ hình học. Điều này có thể giải thích cho lý do tại sao chúng ta vẫn quan niệm x2 và x3 là x bình phương và x lập phương thay vì x mũ hai và x mũ ba. Cũng rất quan trọng đối với tác phẩm của Zeno với cường độ (số vô tỉ) không thể đo lường được là trọng tâm cơ bản trong lý luận suy diễn xuất phát từ sự tan vỡ nền tảng của toán học Hy Lạp trước đó. Việc nhận ra rằng một số quan niệm cơ bản trong lý thuyết hiện tại là mâu thuẫn với thực tế cần phải có một cuộc điều tra đầy đủ và kỹ lưỡng về các tiên đề và giả định làm nền tảng cho lý thuyết đó. Xuất phát từ sự cần thiết này, Eudoxus đã phát triển phương pháp cạn kiệt của mình, một loại chứng minh phản chứng mà "đã thành lập cách thức suy diễn trên cơ sở các tiên đề rõ ràng, cũng như khẳng định và củng cố cho cách thức chứng minh trước đó. Phương pháp cạn kiệt này là bước đầu tiên trong việc tạo ra môn vi tích phân.
Theodorus của Cyrene chứng minh tính vô tỷ của khai căn của các số nguyên lên đến khai căn của các số nhỏ hơn 17, nhưng dừng lại ở đó có lẽ vì đại số ông sử dụng không thể được áp dụng cho căn bậc n của 17.[12]
Chỉ đến khi mà Eudoxus phát triển một lý thuyết về tỷ lệ có tính đến các tỷ lệ là số vô tỉ cũng như tỉ lệ là số hữu tỉ, một nền tảng toán học mạnh mẽ của các số vô tỉ mới được tạo ra.[13]
Biểu diễn thập phân[sửa | sửa mã nguồn]
Có thể dùng biểu diễn thập phân (hay sự biểu diễn của một số trong hệ thập phân) của một số để định nghĩa số hữu tỉ và số vô tỉ.
Nếu như mọi số hữu tỉ đều có biểu diễn thập phân hoặc hữu hạn (số thập phân hữu hạn, ví dụ: ) hoặc vô hạn tuần hoàn (số thập phân vô hạn tuần hoàn, ví dụ: ) thì số vô tỉ có biểu diễn thập phân vô hạn nhưng không tuần hoàn (ví dụ: .)
Một số thực là số vô tỉ khi và chỉ khi biểu diễn liên phân số của nó là vô hạn.
Các ví dụ về cách chứng minh[sửa | sửa mã nguồn]
Căn bậc hai của 2[sửa | sửa mã nguồn]
- Giả sử rằng là một số hữu tỉ. Tức là √2 có thể viết được dưới dạng a/b với a và b là 2 số nguyên dương nguyên tố cùng nhau (vì √2 >0)
- có thể được viết dưới dạng: với a, b là hai số nguyên dương nguyên tố cùng nhau (vì √2 >0)
- Khi đó
- Nên chia hết cho suy ra a chia hết cho b (vì a và b là 2 số nguyên dương)
- Suy ra mâu thuẫn với giả thiết a và b là 2 số nguyên dương nguyên tố cùng nhau ở (1)
Vậy nên giả sử là một số hữu tỉ là sai và ta có kết luận là số vô tỉ.
Cách chứng minh trên có thể được tổng quát hóa để chứng tỏ rằng: "căn bậc hai của một số tự nhiên bất kì hoặc là một số nguyên hoặc là một số vô tỉ."
Các cách chứng minh khác[sửa | sửa mã nguồn]
Để chứng minh: " là một số vô tỉ" người ta còn dùng phương pháp phản chứng theo cách khác, cách này ít nổi tiếng hơn cách ở trên.
- Giả sử rằng là một số hữu tỉ. Điều này có nghĩa là tồn tại hai số nguyên dương m và n sao cho
- Biến đổi đẳng thức trên, ta có:
- Vì > 1, nên từ (1) suy ra
- Từ (2) và (3) suy ra là phân số rút gọn của phân số
Từ (4) suy ra, không thể là phân số tối giản hay không thể là số hữu tỉ - mâu thuẫn với giả thiết là một số hữu tỉ. Vậy phải là số vô tỉ.
Cách chứng minh trên tương tự với cách dùng phép dựng hình để chứng minh giả thuyết về số - một loại phương pháp chứng minh được sử dụng bởi các nhà hình học Hy Lạp cổ đại. Xét một tam giác vuông cân mà độ dài tương ứng của các cạnh góc vuông và cạnh huyền là hai số nguyên dương n và m. Áp dụng Định lý Pytago, ta suy ra tỉ số bằng . Mặt khác, bằng phương pháp dựng hình cổ điển com-pa và thước thẳng ta dựng được một tam giác vuông cân nhỏ hơn với độ dài của các cạnh góc vuông và cạnh huyền tương ứng bằng và . Áp dụng Định lý Pytago cho tam giác thứ hai, ta suy ra tỉ số cũng bằng . Như vậy, , điều này chứng tỏ phân số không thể là phân số tối giản hay không phải là số hữu tỉ mà phải là số vô tỉ.
Căn bậc hai của 10[sửa | sửa mã nguồn]
Giả sử là số hữu tỉ, tức là bằng , vậy:
- trong đó m, n là số nguyên
Tuy nhiên, trong hệ thập phân, bất kỳ số bình phương nào cũng có số chẵn số 0 ở cuối. (Chứng minh: Bất kỳ số nguyên n nào, trong hệ thập phân, đều có dạng: , trong đó a không kết thúc bằng số 0. Vậy bất kỳ số bình phương nào cũng có dạng: .)
Như vậy, trong đẳng thức ở trên, vế trái có số chẵn số 0 ở cuối, nhưng vế phải lại có số lẻ số 0 ở cuối. Vậy giả thiết là số hữu tỉ phải sai.
Căn bậc ba của 2[sửa | sửa mã nguồn]
Giả sử A = là một số hữu tỉ. Có nghĩa là tồn tại m, n là số nguyên sao cho . Suy ra A là nghiệm hữu tỉ của phương trình:
;
Suy ra m là ước của 2, n là ước của 1. Tuy nhiên không có m nào là ước của 2 mà lũy thừa 3 bằng 2. Vậy A là vô tỉ.
Căn bậc n của tất cả các số nguyên tố[sửa | sửa mã nguồn]
Dùng cùng phương pháp này, ta có thể chứng minh rằng căn bậc n của bất kỳ số nguyên nào cũng phải hoặc là số nguyên hoặc là số vô tỉ.
Lấy số nguyên bất kỳ r.
- Ví dụ, r = 2.
Trong hệ nhị phân,
Vậy, như ở trên, nếu = thì, trong hệ nhị phân:
- trong đó m, n là số nguyên
Trường hợp n = 1 không thể xảy ra, vì ta biết không phải là số nguyên.
Lập luận như trên, vế trái có số chẵn số 0 (trong hệ nhị phân) ở cuối, nhưng vế phải lại có số lẻ số 0 ở cuối. Vậy giả thiết là số hữu tỉ phải sai.
- Với số nguyên r bất kỳ, cũng chứng minh như trên trong hệ r - phân:
- trong đó m, n là số nguyên
Nếu n = 1 thì , vậy là số nguyên.
Còn nếu n ≠ 1 thì, như trên, một số bình phương trong hệ r - phân phải có số chẵn số 0 (trong hệ r - phân) ở cuối. Do đó trong đẳng thức này vế trái có số chẵn số 0 ở cuối nhưng vế phải lại có số lẻ số 0 ở cuối. Vậy không thể là số hữu tỉ.
Tỉ lệ vàng[sửa | sửa mã nguồn]

Điểm I chia đoạn thẳng AB theo tỉ lệ vàng nếu A, I, B thẳng hàng và
với Ai > IB
Tỉ số vàng là một số vô tỉ. Thật vậy, giả sử tỉ số này là một số hữu tỉ, thì nó có dạng phân số tối giản là , với x là chiều dài của cả đoạn và a là chiều dài của phần lớn. Suy ra, chiều dài của phần nhỏ là x − a. Và ta có:
Điều này có nghĩa là phân số tối giản được rút gọn thành - một sự vô lý. Sự vô lý này chứng tỏ việc thừa nhận tỉ số φ là số hữu tỉ là sai. Vậy φ là một số vô tỉ.
Lôgarít[sửa | sửa mã nguồn]
Có lẽ, các số vô tỉ dễ nhận ra nhất là các lôgarít. Dưới đây ta sử dụng phương pháp phản chứng để chứng minh rằng log23 là một số vô tỉ:
- Giả sử log23 là một số hữu tỉ. Khi đó tồn tại hai số nguyên dương m và n thỏa mãn: log23 =
- Từ (1) suy ra 2m/n = 3.
- Nâng hai vế của (2) lên lũy thừa bậc n, ta có: 2m = 3n.
- Mặt khác, 2m - lũy thừa cơ số 2 với số mũ nguyên dương luôn lớn hơn 0 và chẵn (vì là tích với ít nhất một thừa số 2), còn 3n - lũy thừa cơ số 3 với số mũ nguyên dương luôn lớn hơn 0 và lẻ (vì là tích của các thừa số lẻ), nên 2m ≠ 3n.
- Từ (3) và (4) suy ra mâu thuẫn, chứng tỏ điều giả sử ban đầu: "log23 là một số hữu tỉ" là sai.
Tương tự, bạn có thể chứng minh cho trường hợp: log102.
Chứng minh e là số vô tỉ[sửa | sửa mã nguồn]
Xem chứng minh ở bài số e.
Số vô tỉ siêu việt và vô tỉ đại số[sửa | sửa mã nguồn]
Một số vô tỉ hoặc là số siêu việt hoặc là số đại số (hay Không đa thức với các hệ số nguyên), trong đó hầu hết các số vô tỉ đều là số siêu việt và số siêu việt là số vô tỉ. Ví dụ: , là các số vô tỉ đại số; còn e và π là các số vô tỉ siêu việt.
Có thể tạo ra các số vô tỉ đại số, bằng cách xét các phương trình đa thức:
Trong đó, các hệ số là số nguyên và
Giả sử rằng có ít nhất một số thực x sao cho (ví dụ, với n lẻ ta luôn tìm được một số x như vậy) thì x là số vô tỉ khi phương trình đa thức trên không có nghiệm hữu tỉ. Nếu đa thức p có nghiệm hữu tỉ thì các nghiệm đó có dạng , trong đó: r là ước của và s là ước của . Vì thế bằng cách thử trực tiếp các giá trị trên bạn có thể biết chúng có phải là nghiệm của p không. Nếu tất cả các giá trị đó đều không là nghiệm của p thì x phải là số vô tỉ.
- Ví dụ, bằng cách trên bạn có thể chỉ ra rằng là một số vô tỉ đại số. Thật vậy, ta có do đó , phương trình thứ hai là một phương trình đa thức không có nghiệm hữu tỉ, vì các giá trị đều không phải là nghiệm của nó.
Để tạo ra các số vô tỉ siêu việt, bạn không thể dùng cách kết hợp các số đại số với nhau, vì các số đại số lập thành một trường, hơn nữa, là một trường đóng. Nhưng bạn có thể dùng cách kết hợp các số siêu việt với các số đại số. Ví dụ: , , và là các số vô tỉ (cũng là các số siêu việt).
Câu hỏi chưa có lời giải[sửa | sửa mã nguồn]
Các số và là số vô tỉ hay không phải là số vô tỉ? Thực tế, chưa ai tìm ra được một cặp số nguyên khác 0 m và n để khẳng định rằng hoặc là số vô tỉ hoặc không phải là số vô tỉ.
Cũng chưa ai khẳng định được các số: , , , hằng số Catalan và hằng số Euler-Mascheroni γ có phải là số vô tỉ hay không.
Mặt khác, theo Công thức Euler thì eiπ + 1 = 0 nên eiπ = -1 lại là một số nguyên, tức là số hữu tỉ
Tập hợp số vô tỉ[sửa | sửa mã nguồn]
Tập hợp số vô tỉ là tập hợp không đếm được (trong khi tập hợp số hữu tỉ là tập hợp đếm được và tập hơp số thực là tập hợp cả số vô tỉ và hữu tỉ. Tập hợp số vô tỉ đại số, hay tập hợp số vô tỉ không siêu việt, là tập hợp đếm được. Tập hợp số vô tỉ dùng giá trị tuyệt đối làm độ đo khoảng cách là một không gian Metric không đầy đủ. Tuy nhiên, không gian Metric này đồng phôi với không gian Metric đầy đủ của tất cả các dãy số nguyên dương; với ánh xạ đồng phôi cho bởi liên phân số mở rộng. Điều đó được chứng minh bằng định lý Baire cho không gian các số vô tỉ. Trong khi, tập hợp các số thực với tính tô-pô thông thường là liên thông, thì không gian Barie, cùng với tính tô-pô như các số thực, được gọi là tô-pô thứ tự, lại hoàn toàn rời rạc: không có một ánh xạ nào đi từ số vô tỉ này đến độ dài của một số vô tỉ khác.
- Tập hợp số vô tỉ: Kí hiệu là
Các tập hợp số[sửa | sửa mã nguồn]
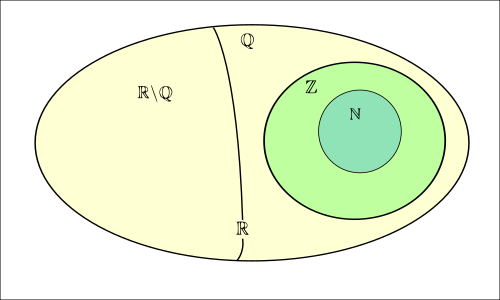
- : Tập hợp số tự nhiên
- : Tập hợp số nguyên
- : Tập hợp số hữu tỉ
- : Tập hợp số vô tỉ
- : Tập hợp số thực
Xem thêm[sửa | sửa mã nguồn]
- Số e
- Số hữu tỉ
- Số nguyên
- Số nguyên tố
- Số tự nhiên
- Số đại số
- Số siêu việt
- Số thực
- Số phức
- Số siêu phức
Tham khảo[sửa | sửa mã nguồn]
- ^ The 15 Most Famous Transcendental Numbers. by Clifford A. Pickover. URL retrieved ngày 24 tháng 10 năm 2007.
- ^ http://www.mathsisfun.com/irrational-numbers.html; URL retrieved ngày 24 tháng 10 năm 2007.
- ^ Weisstein, Eric W., "Irrational Number" từ MathWorld.
- ^ Cantor, Georg (1955) [1915]. Philip Jourdain (biên tập). Contributions to the Founding of the Theory of Transfinite Numbers. New York: Dover. ISBN 978-0-486-60045-1.
- ^ Kurt Von Fritz (1945). “The Discovery of Incommensurability by Hippasus of Metapontum”. The Annals of Mathematics.
- ^ James R. Choike (1980). “The Pentagram and the Discovery of an Irrational Number”. The Two-Year College Mathematics Journal..
- ^ Kline, M. (1990). Mathematical Thought from Ancient to Modern Times, Vol. 1. New York: Oxford University Press. (Original work published 1972). p.33.
- ^ Kline 1990, p. 32.
- ^ Kline 1990, p.34.
- ^ Kline 1990, p.48.
- ^ Kline 1990, p.49.
- ^ Robert L. McCabe (1976). “Theodorus' Irrationality Proofs”. Mathematics Magazine..
- ^ Charles H. Edwards (1982). The historical development of the calculus. Springer.
Liên kết ngoài[sửa | sửa mã nguồn]
- Irrational number tại Encyclopædia Britannica (tiếng Anh)
- Eric W. Weisstein, Irrational Number tại MathWorld.
- Square root of 2 is irrational





















![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)








































