Định lý Pythagoras

Tổng diện tích của hai hình vuông có cạnh là hai cạnh vuông của tam giác vuông (a và b) bằng diện tích của hình vuông có cạnh là cạnh huyền (c).
| Lượng giác |
|---|
 |
| Tham khảo |
| Định lý |
| Vi tích phân |
| Hình học | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||
| Nhà hình học | ||||||||||
|
theo tên
|
||||||||||
|
theo giai đoạn
|
||||||||||
Trong hình học, định lý Pythagoras (hay còn gọi là định lý Py-ta-go) là mối liên hệ căn bản trong hình học Euclid giữa ba cạnh của một tam giác vuông. Định lý phát biểu rằng bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh còn lại. Định lý có thể viết thành một phương trình liên hệ độ dài của các cạnh là a, b và c, thường gọi là "công thức Pythagoras":[1] Đây là định lý cơ bản mà tất cả học sinh trung học cơ sở Việt Nam đã được học ở lớp 7 theo như sách giáo khoa chương trình giáo dục phổ thông năm 2006.
với c là độ dài cạnh huyền, a và b là độ dài hai cạnh góc vuông hay còn được gọi là cạnh kề.
Mặc dù những hiểu biết về mối liên hệ này đã được biết đến từ trước thời của ông,[2][3] nhưng định lý vẫn được đặt tên theo nhà toán học Hy Lạp cổ đại Pythagoras (k. 570–495 TCN) vì - với những tư liệu lịch sử đã ghi lại - ông được coi là người đầu tiên chứng minh được định lý này.[4][5][6] Có một số chứng cứ cho thấy các nhà toán học Babylon đã hiểu về công thức này, mặc dù có ít tư liệu cho thấy họ đã sử dụng nó trong khuôn khổ của toán học.[7][8] Các nhà toán học khu vực Lưỡng Hà, Ấn Độ và Trung Quốc cũng đều tự khám phá ra định lý này và trong một số nơi, họ đã đưa ra chứng minh cho một vài trường hợp đặc biệt.
Có rất nhiều chứng minh cho định lý này - và có lẽ là nhiều nhất trong các định lý của toán học. Cách chứng minh rất đa dạng, bao gồm cả chứng minh bằng hình học lẫn đại số, mà một số có lịch sử hàng nghìn năm tuổi. Định lý Pythagoras còn được tổng quát hóa bằng nhiều cách khác nhau, bao gồm cho không gian nhiều chiều, cho các không gian phi Euclid, cho các tam giác bất kỳ, và thậm chí cho những đối tượng khác xa hẳn so với tam giác vuông, những đối tượng hình học tổng quát trong không gian nhiều chiều. Định lý Pythagoras còn thu hút nhiều sự chú ý từ bên ngoài phạm vi toán học, như là một biểu tượng toán học thâm thúy, bí ẩn, hay sức mạnh của trí tuệ; nó cũng được nhắc tới trong văn học, kịch bản, âm nhạc, bài hát, con tem và phim hoạt hình.
Chứng minh của Pythagoras[sửa | sửa mã nguồn]
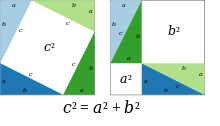
Định lý Pythagoras đã được biết đến từ lâu trước thời Pythagoras, nhưng ông được coi là người đầu tiên nêu ra chứng minh định lý này.[2] Cách chứng minh của ông rất đơn giản, chỉ bằng cách sắp xếp lại hình vẽ.
Trong hai hình vuông lớn ở hình minh họa bên trái, mỗi hình vuông chứa bốn tam giác vuông bằng nhau, sự khác nhau giữa hai hình vuông này là các tam giác vuông được bố trí khác nhau. Do vậy, khoảng trắng bên trong mỗi hình vuông phải có diện tích bằng nhau. Dựa vào hình vẽ, hai vùng trắng có diện tích bằng nhau cho phép rút ra được kết luận của định lý Pythagoras, điều phải chứng minh[9].
Về sau, trong tác phẩm của nhà triết học và toán học Hy Lạp Proclus đã dẫn lại chứng minh rất đơn giản của Pythagoras.[10] Các đoạn dưới đây nêu ra một vài cách chứng minh khác, nhưng cách chứng minh ở trên thuộc về Pythagoras.
Những dạng khác của định lý[sửa | sửa mã nguồn]
Như đã nhắc đến ở đoạn giới thiệu, nếu c ký hiệu là chiều dài của cạnh huyền và a và b ký hiệu là chiều dài của hai cạnh kề, định lý Pythagoras có thể biểu diễn bằng phương trình Pythagoras:
Nếu đã biết chiều dài cả a và b, thì cạnh huyền c tính bằng
Nếu biết độ dài của cạnh huyền c và một trong các cạnh kề (a hoặc b), thì độ dài của cạnh kề còn lại được tìm bằng công thức: hoặc
Phương trình Pythagoras cho liên hệ các cạnh của một tam giác vuông theo cách đơn giản, do đó nếu biết chiều dài của hai cạnh bất kỳ thì sẽ tìm được chiều dài của cạnh còn lại. Một hệ quả khác của định lý đó là trong bất kỳ tam giác vuông nào, cạnh huyền luôn lớn hơn hai cạnh kia, nhưng bé hơn tổng của hai cạnh.
Định lý khái quát định lý này cho tam giác bất kỳ này đó là định lý cos, cho phép tính chiều dài của một cạnh khi biết chiều dài của hai cạnh kia cũng như góc tạo bởi hai cạnh này. Nếu góc giữa hai cạnh này là góc vuông, định lý cos sẽ trở về trường hợp đặc biệt đó là định lý Pythagoras.
Các chứng minh khác[sửa | sửa mã nguồn]
Định lý này có thể coi là định lý có rất nhiều cách chứng minh (luật tương hỗ bậc hai là một định lý khác có nhiều cách chứng minh); trong cuốn sách The Pythagorean Proposition nêu ra 370 cách chứng minh cho định lý Pythagoras.[11]
Chứng minh sử dụng các tam giác đồng dạng[sửa | sửa mã nguồn]

Chứng minh này dựa trên sự tỉ lệ thuận của các cạnh của hai tam giác đồng dạng, tức là nó dựa trên tỉ số của hai cạnh tương ứng của hai tam giác đồng dạng là như nhau với kích thước của tam giác là bất kỳ.
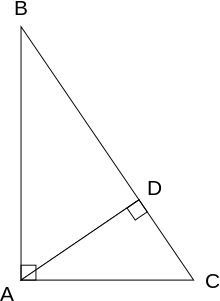
Gọi tam giác ACB là một tam giác vuông, với góc vuông nằm tại đỉnh A, như ở hình bên. Vẽ đường cao tam giác từ điểm C, và gọi H là chân đường cao nằm trên cạnh AB. Điểm H chia chiều dài cạnh huyền c thành hai đoạn AH và BH. Tam giác mới ACH đồng dạng với tam ABC, bởi vì chúng đều có góc vuông (như theo định nghĩa của đường cao), và có chung góc tại đỉnh A, điều này có nghĩa rằng góc thứ ba còn lại cũng bằng nhau, ký hiệu θ như trong hình. Lập luận tương tự, tam giác CBH cũng đồng dạng với tam giác ABC. Chứng minh hai tam giác đồng dạng dựa trên mệnh đề về các góc trong tam giác: tổng các góc trong một tam giác bằng hai lần góc vuông, và tương đương với tiên đề về hai đường thẳng song song. Hai tam giác đồng dạng cho tỉ số của các cạnh tương ứng là bằng nhau:
- và
Tỉ số thứ nhất bằng cosin của góc θ, và tỉ số thứ hai bằng sin của góc này.
Viết lại các tỉ số này
- và
Cộng hai vế của hai đẳng thức
và cuối cùng thu được định lý Pythagoras:
Có nhiều tranh luận xung quanh vai trò của chứng minh này trong lịch sử toán học. Câu hỏi đặt ra là tại sao Euclid đã không sử dụng chứng minh này mà ông đã nghĩ ra một cách khác. Một phỏng đoán cho rằng cách chứng minh sử dụng các tam giác đồng dạng bao gồm định lý về tỉ lệ, một chủ đề không được thảo luận cho đến tận khi ông viết cuốn Cơ sở (Elements), và định lý tỉ lệ cần được phát triển thêm ở thời điểm đó.[12][13]
Chứng minh của Euclid[sửa | sửa mã nguồn]

Tóm tắt nội dung chứng minh của Euclid nêu ra trong cuốn Elements. Hình vuông lớn (có cạnh là cạnh huyền) được chia thành hai hình chữ nhật bên trái và phải (xem hình).
Dựng một tam giác có diện tích bằng một nửa diện tích của hình chữ nhật bên trái. Sau đó dựng tam giác khác có diện tích bằng một nửa hình vuông ở cạnh bên trái. Bước tiếp theo là chứng minh hai tam giác này bằng nhau, và do đó diện tích hình vuông bên trái bằng diện tích hình chữ nhật bên trái. Lập luận tương tự cho hình vuông bên phải và hình chữ nhật bên phải. Tổng diện tích hai hình chữ nhật bằng diện tích hình vuông có cạnh là cạnh huyền, và chính bằng tổng diện tích của hai hình vuông dựng trên hai cạnh kề. Chi tiết chứng minh như sau.
Gọi A, B, C là các đỉnh của một tam giác vuông, với góc vuông tại A. Hạ một đường thẳng từ A vuông góc với cạnh huyền. Đường thẳng này chia hình vuông dựng trên cạnh huyền làm hai hình chữ nhật, mà sẽ chứng minh là hai hình chữ nhật này lần lượt bằng diện tích với hai hình vuông trên hai cạnh góc vuông.
Để chứng minh chặt chẽ, đòi hỏi dựa trên bốn bổ đề cơ bản sau:
- Nếu hai tam giác có hai cạnh tương ứng bằng nhau, và góc giữa hai cạnh này cũng bằng nhau, thì hai tam giác này bằng nhau (trường hợp cạnh-góc-cạnh).
- Diện tích tam giác bằng một nửa diện tích của hình bình hành có cùng đáy và chiều cao.
- Diện tích của hình chữ nhật bằng tích của hai cạnh kề nhau.
- Diện tích của hình vuông bằng bình phương cạnh của nó (hệ quả từ bổ đề 3).
Tiếp theo, mỗi hình vuông trên từng cạnh kề được liên hệ với một tam giác tương đẳng với nó, mà tam giác này lại có liên hệ tương đẳng với một hình chữ nhật vừa chia.[14]

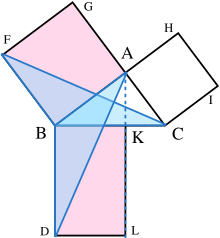
Chứng minh như sau:
- Gọi ABC là tam giác vuông với góc vuông CAB.
- Trên mỗi cạnh BC, AB, và CA, dựng ra các hình vuông tương ứng CBDE, BAGF, và ACIH. Việc dựng các hình vuông cũng đòi hỏi trực tiếp các định lý trước đó nêu ra trong cuốn sách của Euclid, và chỉ phụ thuộc vào tiên đề đường thẳng song song.[15]
- Từ đỉnh A, vẽ một đường thẳng song song với hai cạnh BD và CE. Nó sẽ vuông góc với BC và DE và cắt tại các điểm tương ứng K và L.
- Nối CF và AD, để tạo thành hai tam giác BCF và BDA.
- Góc CAB và BAG đều là các góc vuông; do đó các điểm C, A, và G nằm trên cùng một đường thẳng. Tương tự đối với các điểm B, A, và H.
- Góc CBD và FBA đều là các góc vuông; suy ra góc ABD bằng góc FBC, do cả hai đều bằng tổng của một góc vuông với góc ABC.
- Vì AB bằng FB và BD bằng BC, do đó hai tam giác ABD và FBC bằng nhau.
- Vì A-K-L là đường thẳng song song với cạnh BD, do đó hình chữ nhật BDLK có diện tích bằng hai lần diện tích tam giác ABD bởi vì chúng có chung cạnh đáy BD và cùng đường cao BK, đường vuông góc với cạnh đáy và nối hai đường thằng song song BD và AL. (bổ đề 2)
- Do C nằm trên cùng đường thẳng với A và G, nên hình vuông BAGF có diện tích bằng hai lần diện tích tam giác FBC.
- Từ đó, hình chữ nhật BDLK có diện tích bằng diện tích hình vuông BAGF = AB2.
- Tương tự, chứng minh được hình chữ nhật CKLE có diện tích bằng diện tích hình vuông ACIH = AC2.
- Cộng hai kết quả lại, AB2 + AC2 = BD × BK + KL × KC
- Vì BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC
- Do đó, AB2 + AC2 = BC2, vì CBDE là hình vuông.
Chứng minh này xuất hiện ở Định đề 47 trong tập 1 của cuốn Cơ sở của Euclid,[16] chứng tỏ rằng diện tích của hình vuông trên cạnh huyền bằng tổng diện tích của hai hình vuông trên cạnh kề.[17] Cách chứng minh này khác hẳn với chứng minh dựa trên các tam giác đồng dạng mà Pythagoras đã sử dụng để chứng minh định lý.[13][18]
Các chứng minh bằng cách chia hình và sắp xếp lại[sửa | sửa mã nguồn]
Ở trên đã thảo luận về chứng minh định lý Pythagoras dựa trên phương pháp sắp xếp lại hình. Ý tưởng tương tự cũng được sử dụng cho chứng minh mà miêu tả bằng ảnh động ở dưới bên trái, mà ban đầu có một hình vuông lớn với cạnh bằng a + b, bên trong nó chứa bốn tam giác vuông bằng nhau. Sau đó ảnh động cho thấy các tam giác có hai cách sắp xếp vị trí khác nhau, cách đầu tiên thu được hai hình vuông có cạnh lần lượt là a2 và b2, cách thứ hai chỉ thu được một hình vuông có cạnh c2. Bởi vì hình vuông bao ngoài không thay đổi, và diện tích của bốn tam giác là như nhau ở hai cách sắp xếp hình, do vậy các hình vuông màu đen sẽ phải có diện tích bằng nhau, cho nên a2 + b2 = c2.
Cách chứng minh thứ hai bằng cách sắp xếp lại hình được minh họa ở ảnh động thứ hai. Một hình vuông lớn có diện tích c2 được hình thành từ bốn tam giác vuông bằng nhau có các cạnh a, b và c bao quanh một hình vuông nhỏ ở trung tâm. Sau đó sắp xếp lại hình để thu được hai hình chữ nhật có các cạnh tương ứng a và b bằng cách di chuyển các tam giác. Kết hợp hình vuông nhỏ với hai hình chữ nhật này tạo thành hai hình vuông có diện tích tương ứng là a2 và b2, mà chúng phải có cùng diện tích với hình vuông lớn ban đầu.[19]
Cách thứ ba được miêu tả ở ảnh động ngoài cùng. Hai hình vuông bên trên được chia thành các mảnh với màu lục và lam khác nhau, khi sắp xếp các mảnh này lại có thể đặt vừa vào trong hình vuông ở dưới với cạnh là cạnh huyền của tam giác vuông – hoặc ngược lại, hình vuông lớn ở dưới có thể chia thành các mảnh nhỏ mà sau khi sắp xếp lại các mảnh nhỏ này có thể đặt vừa vào trong hai hình vuông nằm trên hai cạnh góc vuông. Cách cắt một hình thành các phần nhỏ và sắp xếp chúng lại để thu được một hình khác gọi là bài toán phân chia (dissection problem). Từ đó đi đến kết luận là diện tích của hình vuông lớn phải bằng tổng diện tích của hai hình vuông nhỏ.[20]
 |
 |
 |
Chứng minh của Einstein bằng phân tích lập luận[sửa | sửa mã nguồn]
Albert Einstein lúc 11 tuổi đã đưa ra một chứng minh bằng cách phân chia mà không cần thiết phải di chuyển sắp xếp lại các hình.[21] Thay vì sử dụng một hình vuông trên cạnh huyền và hai hình vuông trên hai cạnh kề, ông sử dụng một hình khác bao gồm cạnh huyền, và hai hình đồng dạng mà bao gồm một trong hai cạnh kề thay cho cạnh huyền. Trong chứng minh của Einstein, hình bao gồm cạnh huyền chính là tam giác vuông lớn ban đầu. Thực hiện phân chia tam giác này bằng cách hạ đường cao từ đỉnh của góc vuông xuống cạnh huyền, chia tam giác vuông thành hai tam giác vuông nhỏ hơn. Hai tam giác vuông này đồng dạng với tam giác vuông ban đầu, và có cạnh huyền là cạnh góc vuông của tam giác ban đầu, và tổng diện tích của chúng bằng diện tích tam giác ban đầu. Bởi vì tỉ số diện tích của một tam giác vuông với diện tích của một hình vuông dựng trên cạnh huyền của nó là bằng nhau đối với các tam giác đồng dạng, mối liên hệ giữa diện tích của ba tam giác cũng thỏa mãn cho các hình vuông dựng tương ứng trên các cạnh của hình vuông lớn.
Các chứng minh bằng đại số[sửa | sửa mã nguồn]

Có thể chứng minh định lý bằng phương pháp đại số sử dụng bốn tam giác vuông bằng nhau có cạnh a, b và c, chúng được xếp trong một hình vuông cạnh c như ở hình phía trên của hai hình bên cạnh.[22] Các tam giác có cùng diện tích , trong khi hình vuông nhỏ có cạnh b − a và diện tích (b − a)2. Diện tích của hình vuông lớn sẽ là:
Mà hình vuông này có cạnh là c và diện tích bằng c2, do vậy
Chứng minh tương tự sử dụng bốn tam giác vuông bằng nhau xếp đối xứng xung quanh một hình vuông cạnh c, như ở hình phía dưới.[23] Kết quả cho một hình vuông lớn hơn, với cạnh a + b và diện tích (a + b)2. Bốn tam giác và hình vuông cạnh c phải bằng diện tích của hình vuông lớn hơn,
từ đó

Trước khi trở thành tổng thống Hoa Kỳ, James A. Garfield (khi ấy là Hạ nghị sĩ) đã đưa ra một cách chứng minh cho định lý Pythagoras.[24][25] Thay vì sử dụng một hình vuông ông lại sử dụng hình thang, mà được dựng từ hình vuông trong chứng minh thứ hai ở trên bằng cách chia theo đường chéo của hình vuông bên trong, sẽ thu được hình thang như ở hình vẽ bên cạnh. Diện tích của hình thang khi đó bằng một nửa hình vuông, và bằng
Hình vuông bên trong cũng bị chia một nửa diện tích, và chỉ có hai tam giác vuông còn lại nên có đẳng thức:
Sau khi thu gọn đẳng thức có được điều phải chứng minh.
Chứng minh sử dụng vi tích phân[sửa | sửa mã nguồn]
Có thể đi đến định lý Pythagoras bằng cách nghiên cứu sự thay đổi của một cạnh kề tạo ra thay đổi như thế nào đối với cạnh huyền và áp dụng phương pháp vi tích phân.[26][27][28]
Tam giác vuông ABC có cạnh huyền BC. Tại thời điểm ban đầu, cạnh huyền có độ dài y, cạnh kề AC có độ dài x và cạnh AB có độ dài a, như chỉ ra ở hình vẽ bên dưới.

Sau đó, nếu x dài thêm một lượng vi phân dx bằng cách kéo dài AC một đoạn vô cùng ngắn về điểm D, thì y cũng tăng tương ứng một lượng vi phân dy. Chúng tạo thành hai cạnh của một tam giác, CDE, trong đó (với E được chọn sao cho CE vuông góc với cạnh huyền) nó là tam giác gần đồng dạng với ABC. Do vậy tỉ số giữa các cạnh phải xấp xỉ bằng nhau, tức là:
Viết lại biểu thức thành , hay chính là phương trình vi phân mà giải được bằng cách lấy tích phân hai vế:
thu được
Hằng số tích phân được chọn khi cho x = 0, thì y = a do đó có phương trình
Chứng minh trên chỉ được trình bày một cách trực quan cho dễ hiểu mà thôi. Nếu muốn chặt chẽ (nhưng sẽ khó đọc hơn với người không chuyên ngành vi tích phân), ta có thể dễ dàng viết lại chứng minh này bằng cách thay tích phân không xác định bằng tích phân xác định.
Định lý đảo[sửa | sửa mã nguồn]
Định lý đảo của định lý Pythagoras cũng thỏa mãn:[29]
Với ba số thực dương bất kỳ a, b, và c sao cho a2 + b2 = c2, thì tồn tại một tam giác với ba cạnh tương ứng a, b và c, và mỗi tam giác như thế có một góc vuông giữa hai cạnh a và b.
Phát biểu khác của định lý đảo:
Với một tam giác bất kỳ có ba cạnh a, b, c, nếu a2 + b2 = c2, thì góc giữa a và b bằng 90°.
Định lý đảo cũng được Euclid thảo luận trong cuốn Cơ sở (tập I, mệnh đề 48):[30]
"Nếu trong một tam giác có bình phương một cạnh bằng tổng bình phương của hai cạnh còn lại, thì góc tạo bởi hai cạnh này là góc vuông của tam giác."
Có thể chứng minh định lý đảo Pythagoras bằng cách sử dụng định lý cos hoặc chứng minh như sau:
Gọi ABC là tam giác với các cạnh a, b, và c, với a2 + b2 = c2. Dựng một tam giác thứ hai có các cạnh bằng a và b và góc vuông tạo bởi giữa chúng. Theo định lý Pythagoras thuận, cạnh huyền của tam giác vuông thứ hai này sẽ bằng c = √a2 + b2, và bằng với cạnh còn lại của tam giác thứ nhất. Bởi vì cả hai tam giác có ba cạnh tương ứng cùng bằng chiều dài a, b và c, do vậy hai tam giác này phải bằng nhau. Do đó góc giữa các cạnh a và b ở tam giác đầu tiên phải là góc vuông.
Chứng minh định lý đảo ở trên sử dụng chính định lý Pythagoras. Cũng có thể chứng minh định lý đảo mà không cần sử dụng tới định lý thuận.[31][32]
Một hệ quả của định lý Pythagoras đảo đó là cách xác định đơn giản một tam giác có là tam giác vuông hay không, hay nó là tam giác nhọn hoặc tam giác tù. Gọi c là cạnh dài nhất của tam giác và có a + b > c (nếu không sẽ không tồn tại tam giác vì đây chính là bất đẳng thức tam giác). Các phát biểu sau đây là đúng:[33]
- Nếu a2 + b2 = c2, thì tam giác là tam giác vuông.
- Nếu a2 + b2 > c2, nó là tam giác nhọn.
- Nếu a2 + b2 < c2, thì nó là tam giác tù.
Edsger W. Dijkstra đã phát biểu mệnh đề về tam giác nhọn, vuông và tù bằng các ký hiệu như sau:
- sgn(α + β − γ) = sgn(a2 + b2 − c2),
với α là góc đối diện với cạnh a, β là góc đối diện với cạnh b, γ là góc đối diện với cạnh c, và sgn là hàm signum.[34]
Hệ quả và các áp dụng[sửa | sửa mã nguồn]
Bộ ba số Pythagoras[sửa | sửa mã nguồn]
Một bộ ba số Pythagore là ba số nguyên dương a, b, và c, sao cho a2 + b2 = c2. Nói cách khác, bộ ba số Pythagore biểu diện độ dài của các cạnh của một tam giác vuông mà cả ba độ dài này là những số nguyên dương.[1] Các chứng cứ từ những điểm khảo cổ ở miền bắc châu Âu cho thấy người cổ đại đã biết đến những bộ ba này trước điểm có những văn tự ghi chép lại. Các bộ ba này thường được viết là (a, b, c). Một số bộ hay gặp là (3, 4, 5) và (5, 12, 13).
Một bộ ba số Pythagoras gọi là bộ ba số Pythagoras nguyên thủy khi các số a, b và c nguyên tố cùng nhau (hay ước số chung lớn nhất của a, b và c bằng 1).
Dưới đây liệt kê các bộ ba số Pythagoras nguyên thủy nhỏ hơn 100 (16 bộ số):
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Dựng đoạn thẳng vô ước[sửa | sửa mã nguồn]

Một trong các hệ quả của định lý Pythagoras đó là cho phép dựng được các đoạn thẳng vô ước (incommensurable) (tỉ số của chúng không phải là một số hữu tỉ) bằng thước kẻ và compa. Định lý cho phép dựng các đoạn thẳng vô ước bởi vì cạnh huyền của tam giác vuông liên hệ với hai cạnh kề thông qua phép lấy căn bậc hai.
Hình bên phải cho thấy cách dựng những đoạn thẳng mà độ dài bằng căn bậc hai của một số nguyên dương bất kỳ.[35] Mỗi tam giác có một cạnh (đánh dấu là "1") được chọn sao cho có độ dài bằng một đơn vị. Trong mỗi tam giác vuông, định lý Pythagoras cho phép liên hệ cạnh huyền với độ dài đơn vị của cạnh kề này. Nếu một cạnh huyền bằng căn bậc hai của một số nguyên dương không chính phương, nghĩa là nó có độ dài vô ước với chiều dài đơn vị, như √2, √3, √5 . Chi tiết, xem số vô tỉ bậc hai (quadratic irrational number).
Độ dài vô ước mâu thuẫn với khái niệm của trường phái Pythagoras về các số như là những số hoàn thiện. Trường phái này xét đến các tỷ số của các số nguyên với một đơn vị chung.[36] Theo như một truyền thuyết, nhà triết học Hippasus của Metapontum (ca. 470 B.C.) đã bị ném xuống biển do biết đến sự tồn tại của số vô tỉ hay đoạn thẳng vô ước.[37][38]
Số phức[sửa | sửa mã nguồn]

Với một số phức bất kỳ
thì giá trị tuyệt đối hay mô-đun của nó cho bởi
Do đó ba đại lượng, r, x và y có liên hệ với nhau bởi phương trình Pythagoras,
Chú ý rằng r được xác định là số thực dương hay bằng 0 nhưng x và y có thể nhận giá trị dương hoặc âm tùy ý. Về mặt hình học r là khoảng cách từ z đến điểm O hoặc gốc tọa độ trong mặt phẳng phức.
Dựa vào định nghĩa trên có thể tính được khoảng cách giữa hai điểm, ví dụ z1 và z2. Khoảng cách cho bởi
và đây cũng chính là dạng phương trình Pythagoras,
Khoảng cách Euclid trong các hệ tọa độ khác nhau[sửa | sửa mã nguồn]
Công thức tính khoảng cách trong hệ tọa độ Descartes được suy ra từ định lý Pythagoras.[39] Nếu (x1, y1) và (x2, y2) là tọa độ của hai điểm trên mặt phẳng, thì khoảng cách giữa chúng là, hay còn gọi là khoảng cách Euclid:
Tổng quát hơn, trong không gian Euclid n chiều, khoảng cách Euclid giữa hai điểm, và , được xác định bằng cách tổng quát hóa định lý Pythagoras:
Nếu không sử dụng hệ tọa độ Descartes, ví dụ, mà sử dụng hệ tọa độ cực cho không gian hai chiều hoặc tổng quát hơn, nếu sử dụng hệ tọa độ cong, công thức biểu diễn khoảng cách Euclid sẽ phức tạp hơn so với phương trình Pythagoras, nhưng có thể sử dụng định lý này để tìm ra công thức tính khoảng cách. Ví dụ cụ thể, khoảng cách theo đường thẳng nối giữa hai điểm được tính trong hệ tọa độ cong có thể thấy trong ứng dụng của đa thức Legendre trong vật lý. Công thức khoảng cách được suy ra từ định lý Pythagoras kết hợp với phương trình liên hệ trong phép biến đổi tọa độ từ hệ tọa độ cong sang hệ tọa độ Descartes. Ví dụ, tọa độ cong (r, θ) có liên hệ với tọa độ Descartes là:
Và hai điểm với tọa độ (r1, θ1) và (r2, θ2) cách nhau bằng khoảng cách s:
Thực hiện khai triển bình phương và kết hợp các số hạng lại, công thức Pythagoras cho khoảng cách trong hệ tọa độ Descartes chuyển thành công thức khoảng cách trong hệ tọa độ cực là:
sử dụng đẳng thức lượng giác biến đổi tích thành tổng. Công thức này là định lý cos, mà đôi khi được gọi là công thức tổng quát hóa của định lý Pythagoras.[40] Từ kết quả này, trong trường hợp hai bán kính ở hai vị trí làm thành một góc vuông, hay Δθ = π/2, lúc này thu được một dạng tương tự của công thức Pythagoras: Do đó, định lý Pythagoras cho tam giác vuông trở thành một trường hợp đặc biệt của định lý cos, mà đúng cho tam giác bất kỳ.
Đẳng thức lượng giác Pythagoras[sửa | sửa mã nguồn]

Trong tam giác vuông với hai cạnh kề a, b và cạnh huyền c, lượng giác xác định sin và cos của góc θ giữa cạnh a và cạnh huyền như sau:
Từ đây rút ra:
với bước cuối cùng áp dụng định lý Pythagoras. Liên hệ giữa sin và cos đôi lúc được gọi là đồng nhất thức lượng giác Pythagoras cơ bản.[41] Ở các tam giác đồng dạng, tỉ số các cạnh là như nhau bất kể kích thước của tam giác là như thế nào, và tỉ số chỉ phụ thuộc vào góc giữa chúng. Hệ quả là, trong hình, tam giác với cạnh huyền bằng độ dài đơn vị có độ dài hai cạnh kề là sin θ và cos θ theo đơn vị của cạnh huyền.
Liên hệ với tích vectơ[sửa | sửa mã nguồn]

Định lý Pythagoras liên hệ tích vectơ (hay tích trực tiếp) và tích vô hướng theo cách tương tự:[42]
Kết quả này có thể thấy từ định nghĩa của tích trực tiếp và tích vô hướng
với n là vectơ trực chuẩn đơn vị của cả a và b. Mối liên hệ tuân theo các định nghĩa này và từ đồng nhất thức lượng giác Pythagoras.
Liên hệ trên cũng có thể sử dụng để định nghĩa tích trực tiếp. Bằng cách sắp xếp lại thu được phương trình
Phương trình này có thể coi như là điều kiện xác định cho tích trực tiếp, cũng như cho phần định nghĩa của nó, ví dụ như trong không gian bảy chiều.[43][44]
Tổng quát hóa[sửa | sửa mã nguồn]
Các hình đồng dạng trên ba cạnh tam giác[sửa | sửa mã nguồn]
Nhà toán học Hippocrates của Chios ở thế kỷ V TCN đã tổng quát hóa định lý Pythagoras mở rộng diện tích không chỉ cho các hình vuông trên ba cạnh của tam giác mà còn cho các đa giác đồng dạng,[45] và đã được Euclid đưa vào cuốn Cơ sở:[46]
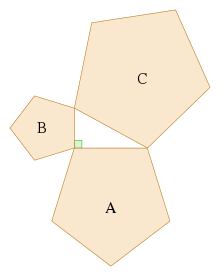
Nếu dựng các hình đồng dạng (xem hình học Euclid) tương ứng trên các cạnh của một tam giác vuông, thì tổng diện tích của hai hình trên hai cạnh kề bằng diện tích của hình dựng trên cạnh huyền.
Sự mở rộng này giả thiết rằng các cạnh của tam giác ban đầu là tương ứng với các cạnh của ba hình đồng dạng (do vậy tỉ số chung giữa các cạnh của ba tam giác này là a:b:c).[47] Trong khi chứng minh của Euclid chỉ áp dụng cho các đa giác lồi, định lý cũng áp dụng cho các đa giác lõm và thậm chí cho các hình đồng dạng có biên cong (nhưng vẫn phải có một cạnh bằng cạnh của tam giác vuông ban đầu).[47]
Ý tưởng cơ bản đằng sau sự mở rộng này đó là diện tích của một hình phẳng tỉ lệ với bình phương của một độ dài bất kỳ, và đặc biệt là tỉ lệ với bình phương của độ dài của một cạnh của tam giác. Do đó, nếu các hình đồng dạng với diện tích tương ứng A, B và C được dựng lên các cạnh tương ứng của tam giác vuông a, b và c thì:
Nhưng theo định lý Pythagoras, a2 + b2 = c2, do vậy A + B = C.
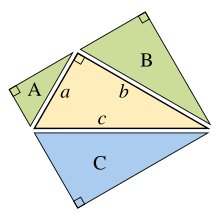
Ngược lại, nếu có thể chứng minh rằng A + B = C cho ba hình đồng dạng mà không sử dụng định lý Pythagoras, thì có thể quay ngược lại để đưa ra một chứng minh cho định lý. Ví dụ, tam giác vuông ở trung tâm có thể dựng lại được và sử dụng tam giác C đặt trên cạnh huyền của nó, và hai tam giác (A và B) dựng trên hai cạnh kề, dựng bằng cách chia tam giác ở trung tâm bởi đường cao kéo từ đỉnh góc vuông. Tổng của diện tích hai tam giác đồng dạng nhỏ do đó sẽ bằng tam giác thứ ba, hay A + B = C và đảo lại điều trên dẫn đến định lý Pythagoras a2 + b2 = c2.
 (diện tích màu lục) A + B = C (diện tích lam). |
 |
 |
Định lý cos[sửa | sửa mã nguồn]

Định lý Pythagoras là trường hợp đặc biệt của định lý tổng quát hơn liên hệ giữa các cạnh của một tam giác bất kỳ, đó là định lý cos:[48]
với θ là góc tạo bởi hai cạnh a và b.
Khi θ bằng 90 độ (π/2 radian), thì cosθ = 0, và công thức quy về công thức Pythagoras.
Tam giác bất kỳ[sửa | sửa mã nguồn]

Cho một tam giác bất kỳ với ba cạnh a, b, c, chọn một trong ba đỉnh của tam giác, dựng lên cạnh đối diện hai điểm sao cho thu được tam giác cân có góc cân bằng góc θ của đỉnh đã chọn. Giả sử góc θ đã chọn đối diện với cạnh có độ dài c của tam giác. Cách dựng như sau: dựng tam giác ABD với điểm D nằm trên cạnh BC và có góc ADB bằng θ cạnh BD bằng r. Tương tự dựng một tam giác thứ hai có góc θ đối diện với cạnh b và độ dài cạnh s dọc cạnh c, như ở hình bên cạnh. Nhà toán học trung cổ Thābit ibn Qurra phát hiện các cạnh của những tam giác này có mối liên hệ như sau:[50][51]
Khi góc θ tiến về π/2, cạnh của tam giác cân thu hẹp lại, và độ dài r và s chồng lên nhau ít hơn. Khi θ = π/2, tam giác ADB trở thành tam giác vuông, và r + s = c, và định lý trở về định lý Pythagoras.
Chứng minh định lý trên khá dễ dàng. Vì tam giác ABC và ABD có hai góc bằng nhau, chung một góc ở đỉnh B, và có hai góc bằng θ, do đó ABC đồng dạng với tam giác ABD. Lấy tỉ số giữa hai cạnh chung góc θ và kề góc này,
Tương tự cho tam giác còn lại, có
Biến đổi hai tỉ số trên và cộng hai vế lại:
thu được điều phải chứng minh.
Định lý vẫn đúng cho tam giác có góc tù , khi đó hai đoạn r và s không chồng lên nhau.
Tam giác bất kỳ và các hình bình hành dựng trên các cạnh[sửa | sửa mã nguồn]
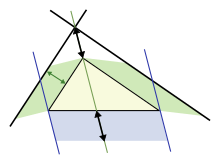
diện tích màu lam bằng diện tích màu lục.

Định lý diện tích Pappus là một cách mở rộng khác, áp dụng cho một tam giác bất kỳ, sử dụng các hình bình hành dựng trên ba cạnh của tam giác này (và hình vuông là trường hợp đặc biệt khi tam giác là tam giác vuông và hình bình hành trở thành hình vuông). Hình trên bên phải minh họa cách dựng các hình bình hành: Đầu tiên dựng hai hình bình hành bất kỳ trên hai cạnh của tam giác, sau đó dựng hình bình hành thứ ba (hai cạnh ngoài cùng của hai hình bình hành cắt nhau tại một điểm, và dựng hình bình hành thứ ba có cạnh bằng độ dài của mũi tên màu đen). Định lý phát biểu rằng diện tích của hình bình hành thứ ba bằng tổng diện tích của hai hình bình hành ban đầu. Sự thay thế hình vuông bằng các hình bình hành mang lại sự tương tự rất giống với định lý Pythagoras gốc. Định lý này mang tên nhà toán học Pappus của Alexandria sống ở thế kỷ IV của Công Nguyên.[52][53]
Hình bên dưới chỉ ra cách chứng minh cho định lý này. Tập trung vào hình bình hành bên trái trước. Hình bình hành màu lục có cùng diện tích với phần hình bình hành màu lam do có chung cạnh đáy b và chiều cao h. Mặt khác, hình bình hành màu lục lại bằng chính hình bình hành thứ nhất ở trên, do chúng có chung cạnh đáy (là cạnh của tam giác) và chung chiều cao. Lặp lại lập luận trên cho hình bình hành thứ hai ở bên phải, sau đó cộng lại thu được điều phải chứng minh.
Hình học không gian[sửa | sửa mã nguồn]
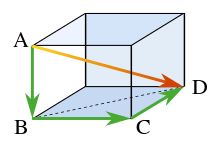

Trong hình học không gian, định lý Pythagoras có thể áp dụng như sau. Xét một hình hộp chữ nhật như ở hình bên.Theo định lý Pythagoras, đường chéo BD bằng:
do ba cạnh này làm thành một tam giác vuông BCD. Sử dụng đường chéo BD và cạnh đứng AB cho tam giác vuông ABD, độ dài đường chéo AD tính được nhờ áp dụng một lần nữa định lý Pythagoras:
và kết hợp với kết quả trên cho:
Kết quả này minh họa cho độ lớn của một vectơ v (đường chéo AD) biểu diễn theo các thành phần trực giao của nó {vk} (ở trên là ba thành phần trực giao):
Từ công thức trên có thể coi là bước tổng quát của định lý Pythagoras cho không gian nhiều chiều hơn. Tuy vậy, kết quả này chỉ là lặp lại ứng dụng của định lý Pythagoras cho không gian hai chiều cho các tam giác vuông ở các mặt phẳng trực giao.
Một dạng tổng quát hơn của định lý Pythagoras cho không gian ba chiều là định lý de Gua, đặt tên theo Jean Paul de Gua de Malves: Nếu một tứ diện có một góc khối vuông (như góc của một hình lập phương), thì bình phương diện tích của mặt đối diện với góc khối vuông bằng tổng bình phương diện tích của ba mặt còn lại. Kết quả này có thể tổng quát cho "định lý Pythagoras n chiều":[54]
Gọi là các vectơ trực giao trong ℝn. Xét một đơn hình n chiều S với các đỉnh . (coi đơn hình (n − 1) chiều với các đỉnh mà không bao gồm gốc như là "cạnh huyền" của S và phần còn lại các mặt (n − 1) chiều S như là các "chân" của nó.) Thì khi đó bình phương thể tích của "cạnh huyền" của S bằng tổng bình phương thể tích của n chân của nó.
Phát biểu này được minh họa trong ba chiều bằng tứ diện hình bên cạnh. "Cạnh huyền" là mặt đáy của tứ diện ở mặt sau của hình, và "các chân" là ba mặt xuất phát từ đỉnh góc khối vuông. Khi chiều cao từ đỉnh xuống mặt đáy tăng lên, diện tích của ba mặt bên tăng lên, trong khi mặt đáy là cố định. Định lý gợi lý rằng khi chiều cao ở giá trị phù hợp tạo ra một góc vuông ở đỉnh thì có thể áp dụng được định lý Pythagoras tổng quát. Phát biểu theo cách khác:[55]
Cho một đơn hình n-hộp chữ nhật trong không gian n chiều, bình phương của (n − 1)-diện (facet) đối đỉnh góc vuông sẽ bằng tổng bình phương của thành phần (n − 1)-diện còn lại.
Không gian tích trong[sửa | sửa mã nguồn]

Định lý Pythagoras có thể tổng quát hóa ở không gian tích trong,[56] một khái niệm tổng quát hóa của không gian Euclid 2 và 3 chiều. Ví dụ, một hàm số có thể coi như là một vectơ với các thành phần vô hạn trong không gian tích trong, như trong giải tích hàm.[57]
Trong một không gian tích trong, khái niệm vuông góc được thay thế bằng khái niệm trực giao: hai vectơ v và w là trực giao nếu tích trong bằng không. Tích trong là sự tổng quát hóa của tích vô hướng vectơ. Tích vô hướng được gọi là tích trong tiêu chuẩn hay tích trong Euclid. Tuy vậy có thể định nghĩa rất nhiều tích trong khác.[58]
Khái niệm độ dài được thay thế bằng khái niệm chuẩn ||v|| của một vectơ v, định nghĩa như sau:[59]
Trong không gian tích trong, định lý Pythagoras phát biểu rằng với hai vectơ trực giao bất kỳ v và w có
Ở đây các vectơ v và w có thể coi như là hai cạnh kề của tam giác vuông với cạnh huyền cho bởi phép cộng vectơ v + w. Dạng định lý Pythagoras này là hệ quả của các tính chất của không gian tích trong:
với tích trong của hai số hạng chéo bằng không, bởi vì chúng trực giao với nhau.
Định lý Pythagoras được tổng quát hơn nữa ở không gian tích trong khi nó áp dụng cho các vectơ không trực giao với định lý hình bình hành:[59]
nói rằng hai lần tổng bình phương của độ dài các cạnh của hình bình hành bằng tổng bình phương độ dài của các đường chéo hình bình hành. Bất kỳ chuẩn nào thỏa mãn đẳng thức trên thì tự nó là một chuẩn trong một không gian tích trong.[59]
Đẳng thức Pythagoras có thể mở rộng cho nhiều hơn hai vectơ trực giao. Nếu v1, v2,..., vn là những cặp vectơ trực giao trong một không gian tích trong, thì áp dụng định lý Pythagoras liên tiếp cho từng cặp vectơ này (như đã miêu tả đối với 3 cạnh của hình hộp chữ nhật ở phần hình học không gian) thu được phương trình như sau[60]
Hình học phi Euclid[sửa | sửa mã nguồn]
Định lý Pythagoras được suy ra từ các tiên đề trong hình học Euclid, và quả thật, định lý này không còn đúng trong hình học phi Euclid.[61] (Có thể chứng minh được rằng, định lý Pythagoras là tương đương với tiên đề Euclid về đường thẳng song song (tiên đề thứ năm).[62][63]) Nói cách khác, trong hình học phi Euclid, liên hệ giữa các cạnh của một tam giác sẽ có dạng khác công thức Pythagoras. Ví dụ, trong hình học cầu, cả ba cạnh của một tam giác vuông (tương ứng là a, b, và c) chiếm một phần tám mặt cầu đơn vị có độ dài bằng nhau và bằng π/2, và mọi góc của nó cũng là góc vuông, hay không tuân theo định lý Pythagoras nữa bởi vì a2 + b2 ≠ c2.
Ở đây xét đến hai hình học phi-Euclid đó là hình học cầu và hình học hyperbolic phẳng; trong mỗi trường hợp, như đối với hình học Euclid cho các tam giác không vuông, kết quả thay thế công thức Pythagoras bằng định luật cos phù hợp.
Tuy vậy, định lý Pythagoras vẫn còn đúng trong hình học hyperbolic và hình học elliptic nếu điều kiện tam giác vuông được thay thế bằng điều kiện tổng của hai góc bằng góc còn lại, như A+B = C. Lúc đó ba cạnh có liên hệ như sau: tổng diện tích của hình tròn với đường kính a và b bằng diện tích hình tròn có đường kính c.[64]
Hình học cầu[sửa | sửa mã nguồn]

Với bất kỳ một tam giác vuông trên mặt cầu bán kính R (ví dụ, nếu γ trong hình bên là góc vuông), với các cạnh a, b, c, thì ba cạnh liên hệ với nhau theo công thức:[65]
Công thức này là trường hợp đặc biệt của định lý cos trên mặt cầu mà áp dụng cho mọi tam giác cầu:
Bằng cách thể hiện chuỗi Maclaurin cho hàm cos như là khai triển tiệm cận với số hạng còn lại trong ký hiệu O lớn,
có thể chứng minh rằng khi R tiến tới vô hạn và các đối số a/R, b/R, và c/R tiến tới không, liên hệ cầu giữa các cạnh của một tam giác vuông sẽ tiệm cận về dạng công thức Pythagoras trong hình học Euclid. Thay thế khai triển tiệm cận cho mỗi hàm cos trong công thức cầu cho một tam giác vuông thu được
Các hằng số a4, b4, và c4 được gộp vào số hạng O lớn còn lại do chúng độc lập với bán kính R. Liên hệ tiệm cận này có thể làm đơn giản hơn nữa bằng cách thực hiện khai triển tích ở trên, triệt tiêu các số hạng, nhân hai vế với −2, và sắp xếp lại số hạng:
Sau khi nhân lên R2, xuất hiện công thức Pythagoras trong hình học Euclid c2 = a2 + b2 khi coi bán kính R tiến đến vô cùng lớn (do các số hạng còn lại tiến tới không):
Đối với một tam giác nhỏ (a, b << R), có thể bỏ qua hàm cos để tránh mất ý nghĩa (loss of significance), thu được
Hình học hyperbolic[sửa | sửa mã nguồn]

Trong không gian hyperbolic có độ cong đều −1/R2, một tam giác vuông với hai cạnh kề a, b, và cạnh huyền c, liên hệ giữa các cạnh có dạng:[66]
với cosh là hàm cos hyperbolic. Công thức này là một dạng đặc biệt của định lý cos hyperbolic áp dụng cho mọi tam giác hyperbolic:[67]
với γ là góc tại đỉnh đối diện với cạnh c.
Bằng cách sử dụng chuỗi Maclaurin cho hàm cos hyperbolic, cosh x ≈ 1 + x2/2, có thể chứng minh được rằng khi tam giác hyperbolic trở lên vô cùng bé (tức là, khi a, b, và c tiến tới zero), liên hệ hyperbolic cho một tam giác vuông thu về công thức Pythagoras.
Đối với một tam giác vuông nhỏ (a, b << R), cosin hypebolic có thể viết thành dạng sau mà không mất đi độ chính xác lớn
Tam giác vô cùng bé[sửa | sửa mã nguồn]
Với bất kỳ độ cong đều K (mang dấu dương, bằng 0, hoặc âm), trong một tam giác vô cùng bé (|K|a2, |K|b2 << 1) với cạnh huyền c, có thể chứng minh liên hệ như sau
Hình học vi phân[sửa | sửa mã nguồn]

Ở khoảng cách vô cùng bé, trong không gian ba chiều, định lý Pythagoras miêu tả khoảng cách giữa hai điểm gần nhau một khoảng vô cùng bé:
với ds là nguyên tố khoảng cách và (dx, dy, dz) là các thành phần của vectơ nối giữa hai điểm. Những không gian như thế được gọi là không gian Euclid. Tuy nhiên, trong hình học Riemann, biểu thức tổng quát cho mọi hệ tọa độ toàn cục (không chỉ là hệ tọa độ Descartes) và không gian tổng quát (không chỉ đối với không gian Euclid) có dạng:[68]
mà các nhà toán học thường gọi là tensor metric. (Đôi khi, một số nơi gọi thuật ngữ này miêu tả cho tập hợp các hệ số gij.) Nó là một hàm số của vị trí, và dùng để miêu tả trong không gian cong. Một ví dụ đơn giản đó là khoảng cách trong không gian phẳng (không gian Euclid) được biểu diễn trong hệ tọa độ cong. Ví dụ, trong hệ tọa độ cực:
Hoặc trong không-thời gian phẳng của thuyết tương đối hẹp, tenxơ mêtric Minkowski có dạng:
Còn trong không thời gian cong của thuyết tương đối rộng, tenxơ mêtric là nghiệm của phương trình trường Einstein và các điều kiện biên khác, ví dụ nổi tiếng đó là mêtric Schwarzschild viết trong hệ tọa độ cầu sử dụng dấu mêtric (-, +, +, +),:
Lịch sử[sửa | sửa mã nguồn]

Có tranh luận xung quanh liệu định lý Pythagoras được phát hiện ra một lần, hay phát hiện nhiều lần ở nhiều nơi, và ngày phát hiện đầu tiên là không xác định, cũng như thời điểm của chứng minh đầu tiên cho định lý. Theo nhà lịch sử toán học Joran Friberg, bằng chứng cho thấy các nhà toán học ở triều đại Babylon thứ nhất (khoảng thế kỷ XX đến thế kỷ XVI TCN) đã biết đến định lý Pythagoras, mà thời điểm này sớm hơn 1000 năm trước thời Pythagoras. Cũng vì vậy mà nhà thống kê học Stephen Stigler đã đề xuất một định luật cho rằng không có một khám phá khoa học nào được đặt tên theo người đầu tiên khám phá ra nó (định luật đặt tên khám phá khoa học của Stigler).[69] (hình ảnh bản chụp phiến sét chữ tượng hình của người Ai Cập cổ đại ghi lại chứng minh định lý Pythagoras do Viện bảo tồn di sản văn hóa Yale thực hiện đã được sử dụng rộng rãi nhất trong các phương tiện và sách báo.)[70] Trong những nguồn khác, như ở cuốn sách của Leon Lederman và Dick Teresi, đề cập Pythagoras là người đã khám phá ra định lý,[71] mặc dù Teresi sau đó phát biểu rằng người Babylon đã phát triển định lý "ít nhất mười lăm thế kỷ trước khi Pythagoras sinh ra."[72] Có thể chia lịch sử liên quan đến định lý ra làm bốn phần: khám phá và hiểu biết về bộ ba số Pythagoras, hiểu biết về mối quan hệ giữa các cạnh của một tam giác vuông, hiểu biết về các mối quan hệ giữa các cạnh chung một góc trong tam giác, và các chứng minh định lý dựa trên phương pháp suy diễn từ hệ tiên đề.
Bartel Leendert van der Waerden (1903–1996) phỏng đoán rằng bộ ba Pythagoras được phát hiện bằng đại số bởi các nhà toán học Babylon.[73] Được viết vào khoảng 2000 và 1786 TCN, trong "cuộn giấy cói Berlin 6619" của Trung Vương quốc Ai Cập chứa một bài toán mà nghiệm cho bộ ba số Pythagoras 6:8:10, nhưng bài toán này không liên quan đến tam giác vuông. Phiến đất sét Lưỡng Hà Plimpton 322, viết trong giai đoạn 1790 và 1750 TCN trong thời kỳ vua Hammurabi cai trị, chứa nhiều đoạn miêu tả có liên hệ gần gũi với bộ ba số Pythagoras.
Ở Ấn Độ, trong đoạn kinh Sulba Sutra Baudhayana , thời điểm khoảng giữa thế kỷ VIII và V TCN,[74] có chứa danh sách các bộ ba Pythagoras được khám phá ra bằng phương pháp đại số, một phát biểu về định lý Pythagoras, và một chứng minh bằng phương pháp hình học của định lý Pythagoras đối với trường hợp tam giác vuông cân. Đoạn kinh Sutra Sulba Apastamba (c. 600 BC) chứa đựng phương pháp chứng minh bằng số cho định lý Pythagoras đối với tam giác vuông bất kỳ, sử dụng cách tính diện tích hình. Van der Waerden tin rằng "nó chắc chắn dựa trên những truyền thống trước đó". Carl Boyer cho rằng định lý Pythagoras trong kinh Śulba-sũtram có thể bị ảnh hưởng từ toán học của người Lưỡng Hà cổ đại, nhưng không có bằng chứng thuyết phục ủng hộ hay bác bỏ giả thuyết này của ông.[75]

Với nội dung đã được biết trước từ lâu, những các đoạn ghi chép lại còn lưu giữ được từ thế kỷ I TCN, quyển Chu bễ toán kinh (周髀算经) của Trung Hoa cổ đại, (đã được phương Tây dịch thành sách với nhan đề The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven) đưa ra giải thích cho định lý Pythagoras với bộ ba số (3, 4, 5) cho các cạnh của tam giác vuông—ở Trung Quốc gọi là "định lý Thương Cao" (勾股定理).[76][77] Trong triều đại nhà Hán (202 TCN đến 220 SCN), bộ ba Pythagoras xuất hiện trong Cửu chương toán thuật,[78] cùng với đề cập về các tam giác vuông.[79] Một số nhà lịch sử toán học tin rằng định lý này xuất hiện đầu tiên ở Trung Quốc,[80] dưới một tên gọi khác là "định lý Thương Cao" (商高定理),[81] đặt tên theo nhà toán học và thiên văn học sống thời nhà Chu, ông này cùng với Chu Công Đán, đã tập hợp các thư tịch cổ để viết lên Chu bễ toán kinh. Tác phẩm cũng được các bậc hậu bối (như Lưu Huy, Lý Thuần Phong) bổ sung và chỉnh lý dần.[82]
Pythagoras, trong khoảng 569–475 TCN, đã sử dụng phương pháp đại số để lập ra các bộ ba số Pythagoras, theo như bình luận của Proclus về quyển cơ sở của Euclid. Tuy vậy, Proclus cho rằng thời điểm viết vào khoảng 410 và 485 AD. Theo Thomas L. Heath (1861–1940), không có một ghi chép cụ thể về sự tồn tại của định lý Pythagoras trong các văn tự còn lưu lại của Hy Lạp từ 5 thế kỷ sau thời của Pythagoras.[83] Tuy nhiên, khi các sử gia Plutarchus và Cicero ghi nhận định lý có công lao của Pythagoras, họ đã viết như thể những đóng góp của ông được mặc nhiên công nhận và biết đến rộng rãi.[5][84] "Whether this formula is rightly attributed to Pythagoras personally, [...] one can safely assume that it belongs to the very oldest period of Pythagorean mathematics."[38] "Liệu công thức này có đáng thuộc về đóng góp cá nhân của Pythagoras, [...] có thể giả sử một cách an toàn rằng nó thuộc về giai đoạn của toán học Pythagoras từ rất lâu trước đó."[38]
Vào khoảng năm 400 TCN, theo như Proclus, Plato đã đưa ra phương pháp tìm các bộ ba Pythagoras bằng cách kết hợp đại số và hình học. Khoảng năm 300 TCN, trong cuốn Cơ sở của Euclid đã ghi lại chứng minh bằng toán học cổ xưa nhất từng được biết đến cho định lý này.[85]
Ứng dụng[sửa | sửa mã nguồn]
Định lý Pythagoras được dùng để tìm một cạnh của tam giác vuông khi biết độ dài của hai cạnh còn lại trong tam giác, mà không cần biết tới chu vi của tam giác đó.
Định lý Pythagoras đảo dùng để kiểm tra một tam giác có phải là tam giác vuông (hoặc một tam giác không phải là tam giác vuông) mà không cần dùng tới góc vuông, mà chỉ cần biết độ dài ba cạnh của tam giác vuông.
Định lý Pythagoras chỉ được dùng trong tam giác vuông.
Xem thêm[sửa | sửa mã nguồn]
- Nhà toán học Pythagoras
- Định lý lớn Fermat
- Bộ ba số Pythagore
- Định lý lá cờ Anh
- Định lý Ptoleme
- Đại số tuyến tính
Tham khảo[sửa | sửa mã nguồn]
- ^ a b Judith D. Sally; Paul Sally (2007). “Chapter 3: Pythagorean triples”. Roots to research: a vertical development of mathematical problems. American Mathematical Society Bookstore. tr. 63. ISBN 0-8218-4403-2.
- ^ a b Posamentier, Alfred. The Pythagorean Theorem: The Story of Its Power and Beauty, p. 23 (Prometheus Books 2010).
- ^ O'Connor, J J; Robertson, E F (tháng 12 năm 2000). “Pythagoras's theorem in Babylonian mathematics”. School of Mathematics and Statistics. University of St. Andrews, Scotland. Truy cập ngày 25 tháng 1 năm 2017.
In this article we examine four Babylonian tablets which all have some connection with Pythagoras's theorem. Certainly the Babylonians were familiar with Pythagoras's theorem.
- ^ George Johnston Allman (1889). Greek Geometry from Thales to Euclid (ấn bản 2005). Hodges, Figgis, & Co. tr. 26. ISBN 1-4326-0662-X.
The discovery of the law of three squares, commonly called the "theorem of Pythagoras" is attributed to him by – amongst others – Vitruvius, Diogenes Laertius, Proclus, and Plutarch ...
- ^ a b (Heath 1921, Vol I, p. 144)
- ^ According to Heath 1921, Vol I, p. 147, Vitruvius says that Pythagoras first discovered the triangle (3,4,5); the fact that the latter is right-angled led to the theorem.
- ^ a b Otto Neugebauer (1969). The exact sciences in antiquity (ấn bản 2). Courier Dover Publications. tr. 36. ISBN 0-486-22332-9.. For a different view, see Dick Teresi (2003). Lost Discoveries: The Ancient Roots of Modern Science. Simon and Schuster. tr. 52. ISBN 0-7432-4379-X., where the speculation is made that the first column of tablet 322 in the Plimpton collection supports a Babylonian knowledge of some elements of trigonometry. That notion is pretty much laid to rest, however, by Eleanor Robson (2002). “Words and Pictures: New Light on Plimpton 322”. The American Mathematical Monthly. Mathematical Association of America. 109 (2): 105–120. doi:10.2307/2695324. JSTOR 2695324. (pdf file Lưu trữ 2013-09-21 tại Wayback Machine). The generally accepted view today is that the Babylonians had no awareness of trigonometric functions. See also Abdulrahman A. Abdulaziz (2010). "The Plimpton 322 Tablet and the Babylonian Method of Generating Pythagorean Triples". arΧiv:1004.0025 [math.HO]. §2, p. 7.
- ^ Mario Livio (2003). The golden ratio: the story of phi, the world's most astonishing number. Random House, Inc. tr. 25. ISBN 0-7679-0816-3.
- ^ Benson, Donald. The Moment of Proof: Mathematical Epiphanies, pp. 172–173 (Oxford University Press, 1999).
- ^ Maor, Eli. The Pythagorean Theorem: A 4,000-year History, p. 61 (Princeton University Press, 2007).
- ^ (Loomis 1968)
- ^ (Maor 2007, tr. 39)
- ^ a b Stephen W. Hawking (2005). God created the integers: the mathematical breakthroughs that changed history. Philadelphia: Running Press Book Publishers. tr. 12. ISBN 0-7624-1922-9. This proof first appeared after a computer program was set to check Euclidean proofs.
- ^ See for example Pythagorean theorem by shear mapping Lưu trữ 2016-10-14 tại Wayback Machine, Saint Louis University website Java applet
- ^ Jan Gullberg (1997). Mathematics: from the birth of numbers. W. W. Norton & Company. tr. 435. ISBN 0-393-04002-X.
- ^ Elements 1.47 by Euclid. Truy cập ngày 19 tháng 12 năm 2006.
- ^ Euclid's Elements, Book I, Proposition 47: web page version using Java applets from Euclid's Elements by Prof. David E. Joyce, Clark University
- ^ The proof by Pythagoras probably was not a general one, as the theory of proportions was developed only two centuries after Pythagoras; see (Maor 2007, tr. 25)
- ^ Alexander Bogomolny. “Pythagorean theorem, proof number 10”. Cut the Knot. Truy cập ngày 27 tháng 2 năm 2010.
- ^ (Loomis 1968, tr. 113, Geometric proof 22 and Figure 123)
- ^ Schroeder, Manfred Robert (2012). Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. Courier Corporation. tr. 3–4. ISBN 0486134784.
- ^ Alexander Bogomolny. “Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #3”. Cut the Knot. Truy cập ngày 4 tháng 11 năm 2010.
- ^ Alexander Bogomolny. “Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #4”. Cut the Knot. Truy cập ngày 4 tháng 11 năm 2010.
- ^ Published in a weekly mathematics column: James A Garfield (1876). “Pons Asinorum”. The New England Journal of Education. 3 (14): 161. as noted in William Dunham (1997). The mathematical universe: An alphabetical journey through the great proofs, problems, and personalities. Wiley. tr. 96. ISBN 0-471-17661-3. and in A calendar of mathematical dates: ngày 1 tháng 4 năm 1876 Lưu trữ 2010-07-14 tại Wayback Machine by V. Frederick Rickey
- ^ Prof. David Lantz' animation Lưu trữ 2013-08-28 tại Wayback Machine from his web site of animated proofs
- ^ Mike Staring (1996). “The Pythagorean proposition: A proof by means of calculus”. Mathematics Magazine. Mathematical Association of America. 69 (1): 45–46. doi:10.2307/2691395. JSTOR 2691395.
- ^ Bogomolny, Alexander. “Pythagorean Theorem”. Interactive Mathematics Miscellany and Puzzles. Alexander Bogomolny. Truy cập ngày 9 tháng 5 năm 2010.
- ^ Bruce C. Berndt (1988). “Ramanujan – 100 years old (fashioned) or 100 years new (fangled)?”. The Mathematical Intelligencer. 10 (3): 24. doi:10.1007/BF03026638.
- ^ Judith D. Sally; Paul J. Sally Jr. (ngày 21 tháng 12 năm 2007). “Theorem 2.4 (Converse of the Pythagorean theorem).”. Roots to Research. American Mathematical Society. tr. 54–55. ISBN 0-8218-4403-2.
- ^ Euclid's Elements, Book I, Proposition 48 From D.E. Joyce's web page at Clark University
- ^ Casey, Stephen, "The converse of the theorem of Pythagoras", Mathematical Gazette 92, July 2008, 309–313.
- ^ Mitchell, Douglas W., "Feedback on 92.47", Mathematical Gazette 93, March 2009, 156.
- ^ Ernest Julius Wilczynski; Herbert Ellsworth Slaught (1914). “Theorem 1 and Theorem 2”. Plane trigonometry and applications. Allyn and Bacon. tr. 85.
- ^ Dijkstra, Edsger W. (ngày 7 tháng 9 năm 1986). “On the theorem of Pythagoras”. EWD975. E. W. Dijkstra Archive.
- ^ Law, Henry (1853). “Corollary 5 of Proposition XLVII (Pythagoras's Theorem)”. The Elements of Euclid: with many additional propositions, and explanatory notes, to which is prefixed an introductory essay on logic. John Weale. tr. 49.
- ^ Shaughan Lavine (1994). Understanding the infinite. Harvard University Press. tr. 13. ISBN 0-674-92096-1.
- ^ (Heath 1921, Vol I, pp. 65); Hippasus was on a voyage at the time, and his fellows cast him overboard. See James R. Choike (1980). “The pentagram and the discovery of an irrational number”. The College Mathematics Journal. 11: 312–316.
- ^ a b c A careful discussion of Hippasus's contributions is found in Kurt Von Fritz (tháng 4 năm 1945). “The Discovery of Incommensurability by Hippasus of Metapontum”. Annals of Mathematics. Second Series. Annals of Mathematics. 46 (2): 242–264. doi:10.2307/1969021. JSTOR 1969021.
- ^ Jon Orwant; Jarkko Hietaniemi; John Macdonald (1999). “Euclidean distance”. Mastering algorithms with Perl. O'Reilly Media, Inc. tr. 426. ISBN 1-56592-398-7.
- ^ Wentworth, George (2009). Plane Trigonometry and Tables. BiblioBazaar, LLC. tr. 116. ISBN 1-103-07998-0., Exercises, page 116
- ^ Lawrence S. Leff (2005). PreCalculus the Easy Way (ấn bản 7). Barron's Educational Series. tr. 296. ISBN 0-7641-2892-2.
- ^ WS Massey (tháng 12 năm 1983). “Cross products of vectors in higher-dimensional Euclidean spaces” (PDF). The American Mathematical Monthly. Mathematical Association of America. 90 (10): 697–701. doi:10.2307/2323537. JSTOR 2323537. S2CID 43318100. Bản gốc (PDF) lưu trữ ngày 26 tháng 2 năm 2021.
- ^ Pertti Lounesto (2001). “§7.4 Cross product of two vectors”. Clifford algebras and spinors (ấn bản 2). Cambridge University Press. tr. 96. ISBN 0-521-00551-5.[liên kết hỏng]
- ^ Francis Begnaud Hildebrand (1992). Methods of applied mathematics (ấn bản 2). Courier Dover Publications. tr. 24. ISBN 0-486-67002-3.
- ^ Heath, T. L., A History of Greek Mathematics, Oxford University Press, 1921; reprinted by Dover, 1981.
- ^ Euclid's Elements: Book VI, Proposition VI 31: "In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle."
- ^ a b Putz, John F. and Sipka, Timothy A. "On generalizing the Pythagorean theorem", The College Mathematics Journal 34 (4), September 2003, pp. 291–295.
- ^ Lawrence S. Leff (ngày 1 tháng 5 năm 2005). cited work. Barron's Educational Series. tr. 326. ISBN 0-7641-2892-2.
- ^ Howard Whitley Eves (1983). “§4.8:...generalization of Pythagorean theorem”. Great moments in mathematics (before 1650). Mathematical Association of America. tr. 41. ISBN 0-88385-310-8.
- ^ Aydin Sayili (tháng 3 năm 1960). “Thâbit ibn Qurra's Generalization of the Pythagorean Theorem”. Isis. 51 (1): 35–37. doi:10.1086/348837. JSTOR 227603.
- ^ Judith D. Sally; Paul Sally (ngày 21 tháng 12 năm 2007). “Exercise 2.10 (ii)”. Roots to Research: A Vertical Development of Mathematical Problems. tr. 62. ISBN 0-8218-4403-2.
- ^ For the details of such a construction, see George Jennings (1997). “Figure 1.32: The generalized Pythagorean theorem”. Modern geometry with applications: with 150 figures (ấn bản 3). Springer. tr. 23. ISBN 0-387-94222-X.
- ^ Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA, 2010, ISBN 9780883853481, pp. 77–78 (excerpt, tr. 77, tại Google Books )
- ^ Rajendra Bhatia (1997). Matrix analysis. Springer. tr. 21. ISBN 0-387-94846-5.
- ^ For an extended discussion of this generalization, see, for example, Willie W. Wong Lưu trữ 2009-12-29 tại Wayback Machine 2002, A generalized n-dimensional Pythagorean theorem.
- ^ Ferdinand van der Heijden; Dick de Ridder (2004). Classification, parameter estimation, and state estimation. Wiley. tr. 357. ISBN 0-470-09013-8.
- ^ Qun Lin; Jiafu Lin (2006). Finite element methods: accuracy and improvement. Elsevier. tr. 23. ISBN 7-03-016656-6.
- ^ Howard Anton; Chris Rorres (2010). Elementary Linear Algebra: Applications Version (ấn bản 10). Wiley. tr. 336. ISBN 0-470-43205-5.
- ^ a b c Karen Saxe (2002). “Theorem 1.2”. Beginning functional analysis. Springer. tr. 7. ISBN 0-387-95224-1.
- ^ Douglas, Ronald G. (1998). Banach Algebra Techniques in Operator Theory, 2nd edition. New York, New York: Springer-Verlag New York, Inc. tr. 60–61. ISBN 978-0-387-98377-6.
- ^ Stephen W. Hawking (2005). cited work. tr. 4. ISBN 0-7624-1922-9.
- ^
Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (ấn bản 2). tr. 2147. ISBN 1-58488-347-2.
The parallel postulate is equivalent to the Equidistance postulate, Playfair axiom, Proclus axiom, the Triangle postulate and the Pythagorean theorem.
- ^
Alexander R. Pruss (2006). The principle of sufficient reason: a reassessment. Cambridge University Press. tr. 11. ISBN 0-521-85959-X.
We could include...the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem among the other axioms and derive the parallel postulate.
- ^ Victor Pambuccian (tháng 12 năm 2010). “Maria Teresa Calapso's Hyperbolic Pythagorean Theorem”. The Mathematical Intelligencer. 32 (4): 2. doi:10.1007/s00283-010-9169-0.
- ^ Barrett O'Neill (2006). “Exercise 4”. Elementary differential geometry (ấn bản 2). Academic Press. tr. 441. ISBN 0-12-088735-5.
- ^ Saul Stahl (1993). “Theorem 8.3”. The Poincaré half-plane: a gateway to modern geometry. Jones & Bartlett Learning. tr. 122. ISBN 0-86720-298-X.
- ^ Jane Gilman (1995). “Hyperbolic triangles”. Two-generator discrete subgroups of PSL(2,R). American Mathematical Society Bookstore. ISBN 0-8218-0361-1.
- ^ Tai L. Chow (2000). Mathematical methods for physicists: a concise introduction. Cambridge University Press. tr. 52. ISBN 0-521-65544-7.[liên kết hỏng]
- ^ Friberg, Joran (1991). “Methods and Traditions of Babylonian Mathematics” (PDF). Historia Mathematica. 8: 277, 306.
- ^ Lynch, Patrick (12 tháng 4 năm 2016). “A 3,800-year journey from classroom to classroom”. Phys.org. Truy cập ngày 13 tháng 4 năm 2016.
- ^ Lederman, Leon and Teresi, Dick. The God Particle: If the Universe Is the Answer, What Is the Question?, p. 80 (Houghton Mifflin Harcourt 2006).
- ^ Teresi, Dick. Lost Discoveries: The Ancient Roots of Modern Science – from the Babylonians to the Maya, p. 8 (Simon and Schuster 2010).
- ^ (van_der_Waerden 1983, tr. 5) See also Frank Swetz; T. I. Kao (1977). Was Pythagoras Chinese?: An examination of right triangle theory in ancient China. Penn State Press. tr. 12. ISBN 0-271-01238-2.
- ^ Kim Plofker (2009). Mathematics in India. Princeton University Press. tr. 17–18, with footnote 13 for Sutra identical to the Pythagorean theorem. ISBN 0-691-12067-6.
- ^
Carl Benjamin Boyer; Uta C. Merzbach (2011). “China and India”. A history of mathematics, 3rd Edition. Wiley. tr. 229. ISBN 978-0470525487.
Quote: [In Sulba-sutras,] we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. Although Mesopotamian influence in the Sulvasũtras is not unlikely, we know of no conclusive evidence for or against this. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides. Less easily explained is another rule given by Apastamba – one that strongly resembles some of the geometric algebra in Book II of Euclid's Elements. (...)
- ^ Robert P. Crease (2008). The great equations: breakthroughs in science from Pythagoras to Heisenberg. W W Norton & Co. tr. 25. ISBN 0-393-06204-X.
- ^ A rather extensive discussion of the origins of the various texts in the Zhou Bi is provided by Christopher Cullen (2007). Astronomy and Mathematics in Ancient China: The 'Zhou Bi Suan Jing'. Cambridge University Press. tr. 139 ff. ISBN 0-521-03537-6.[liên kết hỏng]
- ^ This work is a compilation of 246 problems, some of which survived the book burning of 213 BC, and was put in final form before 100 AD. It was extensively commented upon by Liu Hui in 263 AD. Philip D Straffin, Jr. (2004). “Liu Hui and the first golden age of Chinese mathematics”. Trong Marlow Anderson; Victor J. Katz; Robin J. Wilson (biên tập). Sherlock Holmes in Babylon: and other tales of mathematical history. Mathematical Association of America. tr. 69 ff. ISBN 0-88385-546-1. See particularly §3: Nine chapters on the mathematical art, pp. 71 ff.
- ^ Kangshen Shen; John N. Crossley; Anthony Wah-Cheung Lun (1999). The nine chapters on the mathematical art: companion and commentary. Oxford University Press. tr. 488. ISBN 0-19-853936-3.
- ^ In particular, Li Jimin; see Centaurus, Volume 39. Copenhagen: Munksgaard. 1997. tr. 193, 205.
- ^ Chen, Cheng-Yih (1996). “§3.3.4 Chén Zǐ's formula and the Chóng-Chã method; Figure 40”. Early Chinese work in natural science: a re-examination of the physics of motion, acoustics, astronomy and scientific thoughts. Hong Kong University Press. tr. 142. ISBN 962-209-385-X.
- ^ Wen-tsün Wu (2008). “The Gougu theorem”. Selected works of Wen-tsün Wu. World Scientific. tr. 158. ISBN 981-279-107-8.
- ^ (Euclid 1956, tr. 351) page 351
- ^ An extensive discussion of the historical evidence is provided in (Euclid 1956, tr. 351) page=351
- ^
Asger Aaboe (1997). Episodes from the early history of mathematics. Mathematical Association of America. tr. 51. ISBN 0-88385-613-1.
...it is not until Euclid that we find a logical sequence of general theorems with proper proofs.
Đọc thêm[sửa | sửa mã nguồn]
- Bell, John L. (1999). The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development. Kluwer. ISBN 0-7923-5972-0.
- Euclid (1956). Translated by Johan Ludvig Heiberg with an introduction and commentary by Thomas L. Heath (biên tập). The Elements (3 vols.). 1 (Books I and II) (ấn bản 1908). Dover. ISBN 0-486-60088-2. On-line text at Euclid
- Heath, Sir Thomas (1921). “The 'Theorem of Pythagoras'”. A History of Greek Mathematics (2 Vols.) . Clarendon Press, Oxford. tr. 144 ff. ISBN 0-486-24073-8.
- Kaplan, Robert and Ellen (2011). Hidden Harmonies: The Lives and Times of the Pythagorean Theorem. New York, NY: Bloomsbury Press. ISBN 978-1-59691-522-0. Bản gốc lưu trữ ngày 3 tháng 10 năm 2011. Truy cập ngày 5 tháng 8 năm 2017.
- Libeskind, Shlomo (2008). Euclidean and transformational geometry: a deductive inquiry. Jones & Bartlett Learning. ISBN 0-7637-4366-6. This high-school geometry text covers many of the topics in this WP article.
- Loomis, Elisha Scott (1968). The Pythagorean proposition (ấn bản 2). The National Council of Teachers of Mathematics. ISBN 978-0-87353-036-1. For full text of 2nd edition of 1940, see Elisha Scott Loomis. “The Pythagorean proposition: its demonstrations analyzed and classified, and bibliography of sources for data of the four kinds of proofs” (PDF). Education Resources Information Center. Institute of Education Sciences (IES) of the U.S. Department of Education. Truy cập ngày 4 tháng 5 năm 2010. Originally published in 1940 and reprinted in 1968 by National Council of Teachers of Mathematics, ISBN 0-87353-036-5.
- Maor, Eli (2007). The Pythagorean Theorem: A 4,000-Year History. Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-12526-8.
- Stillwell, John (1989). Mathematics and Its History. Springer-Verlag. ISBN 0-387-96981-0. Also ISBN 3-540-96981-0.
- Swetz, Frank; Kao, T. I. (1977). Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China. Pennsylvania State University Press. ISBN 0-271-01238-2.
- van der Waerden, Bartel Leendert (1983). Geometry and Algebra in Ancient Civilizations. Springer. ISBN 3-540-12159-5.
Liên kết ngoài[sửa | sửa mã nguồn]
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Định lý Pythagoras. |
(bằng tiếng Anh)
- Pythagorean theorem tại Encyclopædia Britannica (tiếng Anh)
- Dijkstra's generalization
- The Pythagorean Theorem is Equivalent to the Parallel Postulate.
- Euclid, David E. Joyce, ed. (1997) [c. 300 BC]. Elements. Truy cập ngày 30 tháng 8 năm 2006.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết) Quản lý CS1: văn bản dư: danh sách tác giả (liên kết) In HTML with Java-based interactive figures.
- Hazewinkel, Michiel biên tập (2001), “Pythagorean theorem”, Bách khoa toàn thư Toán học, Springer, ISBN 978-1-55608-010-4
- History topic: Pythagoras's theorem in Babylonian mathematics Lưu trữ 2011-06-06 tại Wayback Machine
- Interactive links:
- Interactive proof in Java of the Pythagorean theorem
- Another interactive proof in Java of the Pythagorean theorem
- Pythagorean theorem with interactive animation
- Animated, non-algebraic, and user-paced Pythagorean theorem
- Pythagorean theorem water demo on YouTube
- Pythagorean theorem (more than 70 proofs from cut-the-knot)
- Weisstein, Eric W., "Pythagorean theorem" từ MathWorld.


































































![{\displaystyle 1-{\frac {1}{2}}\left({\frac {c}{R}}\right)^{2}+O\left({\frac {1}{R^{4}}}\right)=\left[1-{\frac {1}{2}}\left({\frac {a}{R}}\right)^{2}+O\left({\frac {1}{R^{4}}}\right)\right]\left[1-{\frac {1}{2}}\left({\frac {b}{R}}\right)^{2}+O\left({\frac {1}{R^{4}}}\right)\right]{\text{ khi }}R\to \infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5cdcae6e06657ae45fdf28507599a554bbe421b)













