Chuỗi Taylor
Trong toán học, chuỗi Taylor của một hàm số là tổng vô hạn của các phần tử biểu diễn bằng các đạo hàm của hàm đó tại một điểm. Với mọi hàm thường gặp, giá trị hàm và tổng chuỗi Taylor bằng nhau khi gần điểm này. Chuỗi Taylor được đặt theo tên nhà toán học Brook Taylor, người giới thiệu chúng trong 1715. Nếu 0 là điểm để tính đạo hàm, thì chuỗi Taylor cũng được gọi là chuỗi Maclaurin, theo Colin Maclaurin, người nghiên cứu trường hợp đặc biệt này của Taylor vào giữa thập niên 1700.
Tổng từng phần của n + 1 phần tử đầu tiên của chuỗi Taylor là đa thức bậc n được gọi là đa thức Taylor bậc n của hàm số. Các đa thức Taylor là các xấp xỉ của hàm số, và thường xấp xỉ tốt hơn khi n tăng. Định lý Taylor tính xấp xỉ sai số của các đa thức đó. Nếu chuỗi Taylor của hàm đó hội tụ, tổng của nó là giới hạn của dãy các đa thức Taylor. Giá trị hàm số có thể khác với tổng của chuỗi Taylor, kể cả khi chuỗi Taylor của nó hội tụ. Một hàm số là hàm giải tích tại điểm x khi nó bằng tổng chuỗi Taylor của nó trên một khoảng mở (hay hình tròn mở trong mặt phẳng phức) nào đó chứa x. Điều này cho thấy hàm số giải tích tại mọi điểm trên khoảng (hay trên hình tròn).
Định nghĩa[sửa | sửa mã nguồn]
Chuỗi Taylor của hàm thực hay phức f (x) khả vi vô hạn tại số thực hay phức a tương ứng là chuỗi lũy thừa sau:
trong đó n! ký hiệu giai thừa của n. Để gọn hơn, bằng cách sử dụng ký hiệu Sigma, công thức trên được viết lại thành
trong đó f(n)(a) ký hiệu đạo hàm thứ n của f tính tại a. Đạo hàm với bậc 0 của f được định nghĩa là chính hàm f và hai giá trị (x − a)0 và 0! đều định nghĩa bằng với 1.
Khi a = 0, chuỗi trên cũng được gọi là chuỗi Maclaurin.[1]
Các ví dụ[sửa | sửa mã nguồn]
Chuỗi Taylor của đa thức bất kỳ là chính đa thức đó.[2]
Chuỗi Maclaurin của 1/1 − x là chuỗi hình học
Bằng cách thay x thành 1 − x, chuỗi Taylor của 1/x tại a = 1 là
Bằng cách tính nguyên hàm của chuỗi Maclaurin trên, ta tìm thấy chuỗi Maclaurin của ln(1 − x), trong đó ln ký hiệu lôgarit tự nhiên:
Chuỗi Taylor tương ứng của ln x tại a = 1 là
và tổng quát hơn thì, chuỗi Taylor của ln x tại điểm a khác không tùy ý là:
Chuỗi Maclaurin của hàm mũ ex là
Khai triển trên đúng là bởi đạo hàm của ex đối với x cũng là ex, và e0 bằng với 1. Do đó ta được (x − 0)n tại tử số và n! tại mẫu số của mỗi phần tử trong chuỗi.
Lịch sử[sửa | sửa mã nguồn]
Triết học gia Hy Lạp Zeno đã xét đến bài toán tính tổng vô hạn các phần tử nhưng kết quả thu được là hữu hạn, nhưng đã bác bỏ nó vì đây là nhiệm vụ bất khả thi;[3] kết quả ra được nghịch lý Zeno. Sau đó, Aristotle đưa ra lời giải cho nghịch lý bằng triết học, nhưng phần toán học thì chưa được giải quyết cho đến khi được giải bởi Archimedes. Qua phương pháp vét cạn của Archimedes, ta mới nhận thấy rằng dù có chia vô hạn một giá trị nào đó thì tổng thu được vẫn là hữu hạn.[4] Lưu Huy độc lập tìm ra phương pháp này vài thế kỷ sau đó.[5]
Trong thế kỷ 14, các ví dụ sớm nhất của chuỗi Taylor và các phương pháp tương tự được nêu bởi Madhava xứ Sangamagrama.[6][7] Mặc dù không bài viết nào của ông còn tồn tại, nhưng những bài viết sau đó của các nhà toán học Ấn Độ cho rằng ông đã tính được một số chuỗi, cụ thể hơn là chuỗi các hàm lượng giác sin, cos, tang, và arctan. Trường toán học và thiên văn của Kerala đã mở rộng thêm công trình của ông với nhiều khai triển chuỗi và xấp xỉ cho tới thế kỷ 16.
Trong thế kỷ 17, James Gregory cũng làm việc với chuỗi này và xuất bản một số chuỗi Maclaurin. Phải tới năm 1715 thì phương pháp tổng quát để xây các chuỗi cho các hàm mà chúng tồn tại mới được đưa bởi Brook Taylor,[8] và sau đó chuỗi này được đặt theo tên ông.
Chuỗi Maclaurin được đặt tên theo Colin Maclaurin, một giáo sư tại Edinburgh, người xuất bản các trường hợp đặc biệt của chuỗi Taylor vào những năm 1700 [9].
Hàm giải tích[sửa | sửa mã nguồn]
Nếu f (x) được xác định bởi chuỗi lũy thừa hội tụ trong hình tròn mở tâm b trên mặt phẳng phức (hay trên khoảng số thực), nó được gọi là hàm giải tích trên miền đó [10]. Do đó, với x thuộc miền đó, và f được cho bởi chuỗi lũy thừa hội tụ sau
Tính đạo hàm bởi x cho công thức trên n lần, rồi đặt x = b thì được:
Vì vậy khai triển chuỗi lũy thừa khi ấy tương đương với chuỗi Taylor. Do đó, hàm số giải tích trong hình tròn mở tâm b khi và chỉ khi chuỗi Taylor của nó hội tụ đến giá trị hàm tại mỗi điểm thuộc hình tròn.
Nếu f (x) bằng với tổng chuỗi Talor tại mọi x thuộc mặt phẳng phức, thì nó được gọi là hàm nguyên [11]. Các đa thức, hàm mũ ex, và các hàm lượng giác sin và cos, là các ví dụ của hàm nguyên. Các ví dụ của các hàm không nguyên bao gồm căn bậc hai, lôgarit, các hàm lượng giác tang, và nghịch đảo của nó, arctan. Đối với các hàm này, chuỗi Taylor không hội tụ khi x xa khỏi b. Nghĩa là chuỗi Taylor phân kỳ tại x khi khoảng cách giữa x và b lớn hơn bán kính hội tụ. Chuỗi Taylor có thể dùng để tính giá trị hàm nguyên tại mọi điểm, nếu giá trị của hàm đó cũng như các đạo hàm của hàm đó đã được tính trước tại một điểm.
Các ứng dụng của chuỗi Taylor cho hàm giải tích bao gồm [12]:
- Các tổng riêng (Các đa thức Taylor) của chuỗi có thể dùng để tính xấp xỉ giá trị hàm. Các xấp xỉ này tốt khi đủ số phần tử được xét.
- Vi phân và tích phân của chuỗi lũy thừa có thể được tính dễ dàng hơn so với hàm ban đầu.
- Hàm giải tích chỉ có thể mở rộng duy nhất thành hàm chỉnh hình trên hình tròn mở trong mặt phẳng phức. Điều này giúp cho ta làm việc trong giải tích phức.
- Chuỗi (đã bị cắt đi một phần) có thể dùng để tính giá trị số của hàm, (bằng cách đưa các đa thức về dạng Chebyshev rồi dùng thuật toán Clenshaw).
- Các phép đại số có thể sử dụng trên biểu diễn chuỗi lũy thừa, ví dụ như công thức Euler đến từ khai triển chuỗi Taylor cho các hàm lượng giác và hàm mũ. Kết quả này quan trọng trong giải tích điều hòa.
- Xấp xỉ sử dụng các phần tử đầu của chuỗi Taylor có thể khiến một số bài toán bất khả thi giải được trong miền được giới hạn; Phương pháp này được sử dụng trong vật lý.
Sai số xấp xỉ và hội tụ[sửa | sửa mã nguồn]



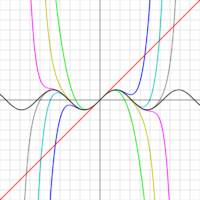
Trong ảnh là xấp xỉ chính xác của hàm sin x quanh điểm x = 0. Đường màu hồng là đa thức Taylor bậc 7:
Sai số của xấp xỉ này không quá | x |9 / 9!. Với một chu kỳ đầy đủ (−π < x < π) sai số này nhỏ hơn 0.08215. Cụ thể hơn, với −1 < x < 1, sai số nhỏ hơn 0,000003.
Ngược lại là ảnh đồ thị của hàm ln(1 + x) và đa thức Taylor của nó quanh a = 0. Các xấp xỉ này hội tụ chỉ khi −1 < x ≤ 1; ngoài miền này các đa thức Taylor tính xấp xỉ kém hơn so với các đa thức trong miền.
Sai số xuất hiện trong xấp xỉ hàm số của đa thức Taylor bậc n được gọi là phần dư Taylor (hay cụ thể hơn, phần dư Taylor bậc n) và được ký hiệu bởi hàm Rn(x):
Trong đó ký hiệu đa thức Taylor bậc n. Định lý Taylor được dùng để xác định cận trên và dưới của phần dư.
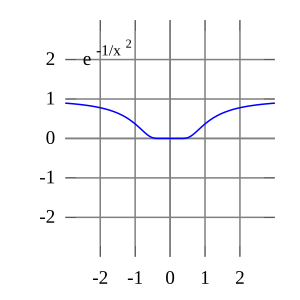
Tổng quát thì, chuỗi Taylor không nhất thiết phải hội tụ. Thêm nữa tập các hàm mà chuỗi Taylor của nó hội tụ là tập meagre trong không gian Fréchet của các hàm trơn[13]. Và kể cả khi chuỗi Taylor của hàm f có hội tụ, giới hạn của nó cũng không nhất thiết phải bằng với giá trị của hàm f (x). Lấy ví dụ, hàm
khả vi vô hạn tại x = 0, và có mọi đạo hàm của nó bằng không tại đó. Do đó, chuỗi Taylor của f (x) quanh x = 0 cũng bằng không. Tuy nhiên, f (x) không phải hàm không, nên không bằng với chuỗi Taylor quanh x = 0. Do đó, hàm f (x) trên là ví dụ của hàm trơn không giải tích.
Trong giải tích thực, ví dụ này cho thấy có vô số các hàm khả vi vô hạn f (x) mà chuỗi Taylor của nó không bằng với f (x) kể cả khi chuỗi hội tụ. Ngược lại, các hàm chỉnh hình trong giải tích phức luôn có chuỗi Taylor của nó hội tụ,thậm chí kể cả các hàm phân hình, dù các hàm đó có các điểm kỳ dị nhưng chuỗi Taylor của nó không bao giờ hội tụ đến giá trị khác với giá trị hàm. Tuy nhiên, hàm phức liên tục e−1/z2, không tiến đến 0 khi z chạy tới 0 theo trục ảo, nên nó không trong mặt phẳng phức và chuỗi Taylor của nó không xác định tại 0.
Tổng quát hơn, mọi dãy số thực hay phức có thể làm hệ số của chuỗi Taylor cho một hàm số khả vi vô hạn trên đường số thực, một hệ quả của bổ đề Borel. Do đó, bán kính hội tụ của chuỗi Taylor có thể bằng không. Có vô hạn các hàm khả vi vô hạn mà chuỗi Taylor của nó có bán kính hội tụ bằng 0 mọi điểm.[14]
Hàm số không thể viết thành chuỗi Taylor tại các điểm kỳ dị; nếu muốn thì, ta vẫn có thể có khai triển chuỗi nếu cho phép sử dụng lũy thừa bậc âm của biến x; xem chuỗi Laurent. Lấy ví dụ, hàm f (x) = e−1/x2 có thể viết thành chuỗi Laurent.
Tổng quát hóa[sửa | sửa mã nguồn]
Tuy nhiên, có dạng tổng quát[15][16] của chuỗi Taylor có hội tụ đến giá trị hàm với bất kỳ hàm liên tục bị chặn trên (0,∞), sử dụng vi tích phân của số gia hữu hạn. Đầy đủ hơn, ta có định lý sau bởi Einar Hille, rằng với bất kỳ t > 0,
Ở đây Δn
h là toán tử số gia hữu hạn thứ n với bước h. Chuỗi này là chuỗi Taylor, nhưng thay vì là đạo hàm thì thay vào đó là số gia: chuỗi này tương tự với chuỗi Newton. Khi hàm f giải tích tại a, các phần tử trong chuỗi hội tụ đến các phần tử trong chuỗi Taylor, do thế mới ám chỉ tổng quát chuỗi Taylor.
Tổng quát thì, với bất kỳ dãy vô hạn ai nào, định thức chuỗi lũy thừa sau được thỏa mãn:
Nên cụ thể hơn thì,
Chuỗi trong vế phải là giá trị kì vọng của f (a + X), trong đó X là biến ngẫu nhiên trong phân phối Poisson lấy giá trị jh với xác suất e−t/h·(t/h)j/j!. Do đó,
Luật số lớn cho rằng định thức này thỏa mãn.[17]
Danh sách các chuỗi Maclaurin cho một số hàm thường gặp[sửa | sửa mã nguồn]
Sau đây là các khai triển chuỗi Maclaurin cho một số hàm thường gặp.[18] Tất cả khai triển này đều đúng với x phức.
Hàm mũ[sửa | sửa mã nguồn]

Hàm mũ (với cơ số e) có chuỗi Maclaurin
- .
Nó hội tụ với mọi x.
Hàm sinh mũ của các số Bell là hàm mũ của số trước đó của hàm mũ:
Lôgarit tự nhiên[sửa | sửa mã nguồn]
Lôgarit tự nhiên (với cơ số e) có chuỗi Maclaurin
Chúng hội tụ với . (Thêm nữa, chuỗi cho ln(1 − x) hội tụ khi x = −1, và chuỗi cho ln(1 + x) hội tụ khi x = 1.)
Chuỗi hình học[sửa | sửa mã nguồn]
Chuỗi hình học và các đạo hàm của nó có chuỗi Maclaurin như sau
Tất cả đều hội tụ cho . Đây là các trường hợp đặc biệt cho chuỗi nhị thức trong mục sau.
Chuỗi nhị thức[sửa | sửa mã nguồn]
Chuỗi nhị thức là chuỗi lũy thừa
(Nếu n = 0, tích này thành tích rỗng và có giá trị 1.) Nó hội tụ cho với bất kỳ số thực hay phức α.
Khi α = −1, chuỗi này trở thành chuỗi hình học trong mục trước. Trường hợp đặc biệt α = 1/2 và α = −1/2 cho hàm căn bậc hai và nghịch đảo của nó:
Khi chỉ có mỗi các phần tử tuyến tính được giữ lại, xấp xỉ này đơn giản hóa thành xấp xỉ nhị thức.
Các hàm lượng giác[sửa | sửa mã nguồn]
Các hàm lượng giác thường gặp và nghịch đảo của chúng có chuỗi Maclaurin như sau:
Tất cả các góc đều trong radian. Các số Bk xuất hiện trong biểu thức tan x là các số Bernoulli. Các số Ek trong khai triển của sec x là các số Euler.
Các hàm Hyperbolic[sửa | sửa mã nguồn]
Các hàm hyperbolic có chuỗi Maclaurin gần giống với các hàm lượng giác:
Các số Bk xuất hiện trong chuỗi cho tanh x là các số Bernoulli.
Hàm Polylogarit[sửa | sửa mã nguồn]
Các hàm polylogarit có định thức sau:
Các hàm chi Legendre được định nghĩa như sau:
Các công thức bên dưới được gọi là nguyên hàm tiếp tuyến nghịch đảo:
Trong cơ học thống kê, các công thức này rất quan trọng.
Hàm Elliptic[sửa | sửa mã nguồn]
Nguyên hàm Elliptic đầy đủ của loại đầu K và loại thứ hai E được định nghĩa như sau:
Các hàm theta Jacobi mô tả thế giới của hàm môđun elliptic và chúng thường có chuỗi Taylor như sau :
Dãy số phân hoạch P(n) có hàm sinh sau:
Dãy số phân hoạch nghiêm ngặt Q(n) có hàm sinh sau:
Tính chuỗi Taylor[sửa | sửa mã nguồn]
Có nhiều phương pháp để tính chuỗi Taylor cho các hàm số khác nhau. Đầu tiên có thể dùng luôn định nghĩa chuỗi Taylor, song làm như vậy yêu cầu phải tổng quát các hệ số theo một nhận dạng dễ nhìn. Ngoài ra, cũng có thể sử dụng các phép cơ bản như phép thế, phép nhân, phép chia hay cộng, trừ của chuỗi Taylor căn bản để tìm chuỗi Taylor cho hàm cần tìm, bởi bản chất của chuỗi Taylor là chuỗi lũy thừa. Trong một số trường hợp, có thể tìm ra chuỗi Taylor bằng cách liên tục áp dụng tích phân từng phần. Tiện hơn nhiều đó là việc dùng các hệ thống đại số máy tính để tính các chuỗi Taylor.
Ví dụ đầu tiên[sửa | sửa mã nguồn]
Để tính đa thức Taylor bậc 7 của hàm sau
- ,
đầu tiên có thể viết lại thành
- .
Chuỗi Taylor cho lôgarit tự nhiên (sử dụng ký hiệu O lớn) là
và cho hàm cosin là
- .
Khai triển của hàm cosin có phần tử bằng không, cho phép thay chuỗi thứ hai vào chuỗi thứ nhất rồi bỏ đi các phần tử có bậc lớn hơn 7 bằng cách sử dụng ký hiệu O lớn:
Bởi hàm cosin là hàm chẵn, hệ số cho các lũy thừa bậc lẻ x, x3, x5, x7, ... đều bằng không.
Ví dụ thứ hai[sửa | sửa mã nguồn]
Giả sử muốn tìm chuỗi Taylor tại 0 cho hàm số
Sau đây là khai triển chuỗi Taylor sau cho hàm
và như ví dụ đầu,
Giả sử chuỗi lũy thừa có dạng
Nhân hai vế với mẫu số rồi thay khai triển chuỗi cho cosin được
Gộp các phần tử cho tới bậc 4 được
Các giá trị của có thể tìm được bằng cách so sánh với các hệ số trên của , ra được:
Ví dụ thứ ba[sửa | sửa mã nguồn]
Ở đây ta dùng "khai triển gián tiếp" để tìm ra khai triển cho hàm số sau. Phương pháp này sử dụng khai triển của hàm mũ. Để khai triển hàm (1 + x)ex thành chuỗi Taylor của x, ta dùng khai triển đã biết của hàm mũ ex:
Từ đó,
Dùng chuỗi Taylor cho định nghĩa[sửa | sửa mã nguồn]
Theo cổ điển, các hàm đại số được định nghĩa bởi phương trình đại số, và các hàm siêu việt (bao gồm các hàm trên) được định nghĩa bởi một số tính chất thêm vào mà chúng thỏa mãn, như phương trình vi phân. Lấy ví dụ, hàm mũ là hàm bằng với đạo hàm của nó tại mọi nơi, nhận giá trị 1 tại gốc tọa độ [19]. Tương tự như vậy, có thể định nghĩa các hàm giải tích bằng các chuỗi Taylor của chúng.
Chuỗi Taylor được sử dụng để định nghĩa các "toán tử" trong nhiều trường của toán học. Cụ thể hơn, điều này đúng khi định nghĩa cổ điển của hàm số không còn đúng nữa. Lấy ví dụ, dùng chuỗi Taylor, ta có thể mở rộng các hàm giải tích cho tập các ma trận và các toán tử, như mũ ma trận hay lôgarit ma trận [20].
Trong các nhánh khác, như giải tích, người ta thường làm việc dễ dàng hơn với chính các chuỗi lũy thừa. Ví dụ chẳng hạn, có thể coi nghiệm của phương trình vi phân là chuỗi lũy thừa, sau đó thử chứng minh xem chuỗi Taylor đó có phải là chuỗi Taylor của nghiệm cần tìm[21].
Chuỗi Taylor cho hàm nhiều biến[sửa | sửa mã nguồn]
Chuỗi Taylor có thể tổng quát hóa cho hàm nhiều biến như sau[22][23]
Lấy ví dụ, đối với hàm phụ thuộc vào hai biến, x và y, chuỗi Taylor của nó đến bậc hai quanh điểm (a, b) là
trong đó các chữ viết dưới ký hiệu đạo hàm riêng tương ứng.
Khai triển chuỗi Taylor bậc hai cho hàm scalar nhiều biến có thể viết gọn lại thành
trong đó D f (a) là gradient của f tính tại x = a và D2 f (a) là ma trận Hesse. Sử dụng ký hiệu đa chỉ số ,chuỗi Taylor cho hàm nhiều biến viết lại thành
vẫn được hiểu là phương trình ban đầu nhưng được viết gọn lại đi, nhìn chung tương tự với trường hợp hàm 1 biến.
Ví dụ[sửa | sửa mã nguồn]

Để tính khai triển chuỗi Taylor bậc hai quanh điểm (a, b) = (0, 0) cho hàm số
đầu tiên cần tính các đạo hàm riêng cần thiết:
Tính các đạo hàm tại gốc tọa độ ra các hệ số Taylor
Thay các hệ số trên vào công thức
ra được
Bởi hàm ln(1 + y) giải tích khi | y | < 1, ta có
So sánh với chuỗi Fourier[sửa | sửa mã nguồn]
Chuỗi Fourier cho phép biểu diễn hàm tuần hoàn (hay hàm được định nghĩa trên khoảng đóng [a,b]) là tổng vô hạn của các hàm lượng giác (sin và cosine). Theo cách hiểu đó, chuỗi Fourier cũng có vẻ tương tự với chuỗi Taylor, bởi chuỗi Taylor cũng là tổng vô hạn nhưng là của các lũy thừa. Song, hai chuỗi này khác nhau tại một số điểm sau[24]:
- Dù có bỏ đi bất cứ hữu hạn số phần tử nào trong chuỗi Taylor của f (x) quanh điểm x = a, thì giá trị chuỗi vẫn bằng với f tại a. Ngược lại, chuỗi Fourier được tính bằng nguyên hàm trên toàn khoảng nên không có điểm nào trong khoảng mà giá trị hàm bằng với giá trị chuỗi.
- Để tính chuỗi Taylor thì cần phải biết hàm số trên một lân cận nhỏ tùy ý của một điểm nào đó, trong khi tính chuỗi Fourier thì cần phải biết hàm số trên toàn bộ miền của nó. Theo cách hiểu đó, có thể nói chuỗi Taylor có tính "địa phương" còn chuỗi Fourier thì mang tính "toàn cục".[25]
- Chuỗi Taylor được định nghĩa cho các hàm có vô hạn đạo hàm tại một điểm, trong khi chuỗi Fourier được định nghĩa cho hàm khả tích. Ví dụ cụ thể như, các hàm mà không đâu khả vi. (Ví dụ, f (x) có thể là hàm Weierstrass.)
- Hội tụ giữa hai chuỗi có các tính chất khác nhau. Kể cả khi chuỗi Taylor có bán kính hội tụ của nó dương, giá trị chuỗi không nhất thiết phải bằng giá trị hàm; nhưng nếu hàm số giải tích thì chuỗi hội tụ từng điểm với hàm, và hội tụ đều trên mọi tập con compact của khoảng hội tụ. Còn đối với chuỗi Fourier, nếu hàm số bình phương khả tích thì hàm số hội tụ trong trung bình toàn phương, nhưng cần có điều kiện thêm vào để đảm bảo hội tụ từng điểm hay hội tụ đều (ví dụ chẳng hạn, nếu hàm tuần hoàn và thuộc lớp C1 thì chuỗi Fourier hội tụ đều).
- Trong ứng dụng, khi muốn tính xấp xỉ một hàm số với hữu hạn số phần tử thì sử dụng đa thức Taylor hoặc tổng riêng của chuỗi các hàm lượng giác, tương ứng với chuỗi Taylor và chuỗi Fourier. Trong trường hợp chuỗi Taylor, thì sai số của nó rất nhỏ trong lân cận của điểm nó được xét, nhưng lại rất lớn khi cách xa điểm đang xét. Đối với chuỗi Fourier thì sai số được phân phối trên toàn miền của hàm số.
Xem thêm[sửa | sửa mã nguồn]
Tham khảo[sửa | sửa mã nguồn]
- ^ Thomas & Finney 1996, §8.9
- ^ Waring, Edward (9 tháng 1 năm 1779). “Problems concerning interpolations”. Philosophical Transactions of the Royal Society. 69: 59–67. doi:10.1098/rstl.1779.0008.
- ^ Lindberg, David (2007). The Beginnings of Western Science (ấn bản 2). University of Chicago Press. tr. 33. ISBN 978-0-226-48205-7.
- ^ Kline, M. (1990). Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press. tr. 35–37. ISBN 0-19-506135-7.
- ^ Boyer, C.; Merzbach, U. (1991). A History of Mathematics . John Wiley and Sons. tr. 202–203. ISBN 0-471-09763-2.
- ^ “Neither Newton nor Leibniz – The Pre-History of Calculus and Celestial Mechanics in Medieval Kerala” (PDF). MAT 314. Canisius College. Lưu trữ (PDF) bản gốc ngày 23 tháng 2 năm 2015. Truy cập ngày 9 tháng 7 năm 2006.
- ^ S. G. Dani (2012). “Ancient Indian Mathematics – A Conspectus”. Resonance. 17 (3): 236–246. doi:10.1007/s12045-012-0022-y. S2CID 120553186.
- ^ Taylor, Brook (1715). Methodus Incrementorum Directa et Inversa [Direct and Reverse Methods of Incrementation] (bằng tiếng La-tinh). London. p. 21–23 (Prop. VII, Thm. 3, Cor. 2). Translated into English in Struik, D. J. (1969). A Source Book in Mathematics 1200–1800. Cambridge, Massachusetts: Harvard University Press. tr. 329–332.
- ^ Answers, All (tháng 11 năm 2018). “History of Maclaurin Series”. Nottingham, UK: UKEssays.com. Truy cập ngày 4 tháng 9 năm 2022.
- ^ Analytic Functions (bằng tiếng Anh). doi:10.1007/978-3-642-85590-0.
- ^ M. A. J. (tháng 2 năm 1956). “Entire Functions. By R. P. Boas. Pp. xi, 276. $6. 1954. (Academic Press, New York)”. The Mathematical Gazette. 40 (331): 70–71. doi:10.2307/3610304. ISSN 0025-5572.
- ^ “Taylor expansions and applications”, Mathematical Analysis I, Milano: Springer Milan, tr. 223–255, 2008, doi:10.1007/978-88-470-0876-2_7, ISBN 978-88-470-0875-5, truy cập ngày 4 tháng 9 năm 2022
- ^ Dayal, S. (1977). “A Converse of Taylor's Theorem for Functions on Banach Spaces”. Proceedings of the American Mathematical Society. 65 (2): 265–273. doi:10.2307/2041904. ISSN 0002-9939.
- ^ Rudin, Walter (1980), Real and Complex Analysis, New Delhi: McGraw-Hill, tr. 418, Exercise 13, ISBN 0-07-099557-5
- ^ Feller, William (1971), An introduction to probability theory and its applications, Volume 2 (ấn bản 3), Wiley, tr. 230–232.
- ^ Hille, Einar; Phillips, Ralph S. (1957), Functional analysis and semi-groups, AMS Colloquium Publications, 31, American Mathematical Society, tr. 300–327.
- ^ Feller, William (1970). An introduction to probability theory and its applications. 2 (ấn bản 3). tr. 231.
- ^ Phần lớn các chuỗi này có thể tìm thấy trong (Abramowitz & Stegun 1970).
- ^ A. Ok, Efe (2011). Real Analysis with Economic Applications. Princeton University Press. tr. 76. Truy cập 27 tháng 08 năm 2022.
- ^ Vetter, William J. (1973). “Matrix Calculus Operations and Taylor Expansions”. SIAM Review. 15 (2): 352–369. ISSN 0036-1445.
- ^ Nedialkov, Nedialko S.; Pryce, John D. (tháng 9 năm 2005). “Solving Differential-Algebraic Equations by Taylor Series (I): Computing Taylor Coefficients”. BIT Numerical Mathematics. 45 (3): 561–591. doi:10.1007/s10543-005-0019-y. ISSN 0006-3835.
- ^ Lars Hörmander (1990), The analysis of partial differential operators, volume 1, Springer, Eqq. 1.1.7 and 1.1.7′
- ^ Duistermaat; Kolk (2010), Distributions: Theory and applications, Birkhauser, ch. 6
- ^ Askey, Richard; Haimo, Deborah (1996). “Similarities Between Fourier and Power Series”. The American Mathematical Monthly. 3 (4): 297–304. doi:10.2307/2975184.
- ^ Bridger, Mark (2011). Real Analysis: A Constructive Approach. John Wiley & Sons. tr. 292. Truy cập 25 tháng 08 năm 2022.
Nguồn khác[sửa | sửa mã nguồn]
- Abramowitz, Milton; Stegun, Irene A. (1970), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover Publications, Ninth printing
- Thomas, George B., Jr.; Finney, Ross L. (1996), Calculus and Analytic Geometry (ấn bản 9), Addison Wesley, ISBN 0-201-53174-7
- Greenberg, Michael (1998), Advanced Engineering Mathematics (ấn bản 2), Prentice Hall, ISBN 0-13-321431-1
Liên kết ngoài[sửa | sửa mã nguồn]
- "Taylor Series" ở MathWorld
- Madhava of Sangamagramma Lưu trữ 2010-04-18 tại Wayback Machine
- "Discussion of the Parker-Sochacki Method" Lưu trữ 2005-12-02 tại Wayback Machine














![{\displaystyle f(x)={\begin{cases}e^{-1/x^{2}}&{\text{nếu }}x\neq 0\\[3mu]0&{\text{nếu }}x=0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d471711c7671f8435c7ffbee268c74523e8159b)






![{\displaystyle \exp[\exp(x)-1]=\sum _{n=0}^{\infty }{\frac {B_{n}}{n!}}x^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/103a0b8da090bd1206e8eeda3c0ab2bcef603602)






![{\displaystyle {\begin{aligned}\sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}&&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots &&{\text{với mọi }}x\\[6pt]\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}&&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots &&{\text{với mọi }}x\\[6pt]\tan x&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)}{(2n)!}}x^{2n-1}&&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots &&{\text{với }}|x|<{\frac {\pi }{2}}\\[6pt]\sec x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}&&=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+\cdots &&{\text{với }}|x|<{\frac {\pi }{2}}\\[6pt]\arcsin x&=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+\cdots &&{\text{với }}|x|\leq 1\\[6pt]\arccos x&={\frac {\pi }{2}}-\arcsin x\\&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&={\frac {\pi }{2}}-x-{\frac {x^{3}}{6}}-{\frac {3x^{5}}{40}}-\cdots &&{\text{với }}|x|\leq 1\\[6pt]\arctan x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{với }}|x|\leq 1,\ x\neq \pm i\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4d7b8d45ee116143daa87c7247c401ea10376ed)
![{\displaystyle {\begin{aligned}\sinh x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}&&=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+\cdots &&{\text{với mọi }}x\\[6pt]\cosh x&=\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}&&=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+\cdots &&{\text{với mọi }}x\\[6pt]\tanh x&=\sum _{n=1}^{\infty }{\frac {B_{2n}4^{n}\left(4^{n}-1\right)}{(2n)!}}x^{2n-1}&&=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots &&{\text{với }}|x|<{\frac {\pi }{2}}\\[6pt]\operatorname {arsinh} x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x-{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}-\cdots &&{\text{với }}|x|\leq 1\\[6pt]\operatorname {artanh} x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}&&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+\cdots &&{\text{với }}|x|\leq 1,\ x\neq \pm 1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5222c1aaa578cd829f0b0ca690ec6cff8751eff)






![{\displaystyle {\frac {2}{\pi }}K(x)=\sum _{n=0}^{\infty }{\frac {[(2n)!]^{2}}{16^{n}(n!)^{4}}}x^{2n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc8e464983f3fdf2071ed149ed55bba842544a2d)
![{\displaystyle {\frac {2}{\pi }}E(x)=\sum _{n=0}^{\infty }{\frac {[(2n)!]^{2}}{(1-2n)16^{n}(n!)^{4}}}x^{2n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85daf53e01f72f0f0c820811910a77974657052e)


![{\displaystyle \vartheta _{00}(x)^{-1/6}\vartheta _{01}(x)^{-2/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{-1/24}=\sum _{n=0}^{\infty }P(n)x^{n}=\prod _{k=1}^{\infty }{\frac {1}{1-x^{k}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c898219336ceb853f972d83f60a14049d671523)
![{\displaystyle \vartheta _{00}(x)^{1/6}\vartheta _{01}(x)^{-1/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{1/24}=\sum _{n=0}^{\infty }Q(n)x^{n}=\prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa5dd403c225903926ad0c45788a5f1a0a5fb67c)





















![{\displaystyle {\begin{aligned}f'_{x}&=e^{x}\ln(1+y)\\[6pt]f'_{y}&={\frac {e^{x}}{1+y}}\\[6pt]f'_{xx}&=e^{x}\ln(1+y)\\[6pt]f'_{yy}&=-{\frac {e^{x}}{(1+y)^{2}}}\\[6pt]f'_{xy}&=f'_{yx}={\frac {e^{x}}{1+y}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/564d54f8538a2ced856bf026845f33f74b9dff7b)



