Ellipsoid
Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin. |


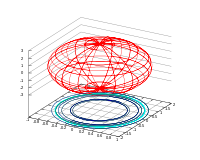
Ellipsoid, hay elipxoit là một dạng mặt bậc hai có hình tương tự như elip trong không gian ba chiều. Phương trình của một ellipsoid chính tắc trong hệ tọa độ Descartes x, y, z là
Trong đó a và b là các bán kính xích đạo (chúng vuông góc với nhau) và c là bán kính cực (nghĩa là độ dài của nửa cực thứ ba). Cả ba đều là các số thực dương, chúng xác định hình dạng của ellipsoid.
Nếu tất cả ba bán kính bằng nhau, ellipsoid trở thành mặt cầu (sphere)); nếu có hai bán kính xích đạo bằng nhau ellipsoid được gọi là một mặt phỏng cầu (spheroid):
- Mặt cầu;
- Phỏng cầu dẹt (mặt cầu dẹt);
- Phỏng cầu dài (mặt cầu dài);
- ellipsoid lệch ("ba chiều khác nhau").
Các phỏng cầu còn được xem là các mặt tròn xoay. Chúng được sinh ra khi quay một đường ellipse chính tắc trên mặt phẳng Oxz (hoặc Oyz) xung quanh trục Oz.
Phần không gian hữu hạn giới hạn bởi mặt ellipsoid, nghĩa là tập các điểm trong hệ Oxyz thỏa mãn bất đẳng thức:
được gọi là khối ellipsoid.
Dạng tham số[sửa | sửa mã nguồn]
Sau đây, gọi là tham số chỉ vĩ độ còn là tham số chỉ kinh độ của các điểm trên một ellipsoid, khi đó ta có dạng tham số của nó:
(Chú ý rằng dạng tham sô không là 1-1 tại các điểm mà .)
Thể tích khối ellipsoid[sửa | sửa mã nguồn]
Thể tích của khối ellipsoid được tính theo (nó rất giống với công thức thể tích hình cầu):
Diện tích mặt ellipsoid[sửa | sửa mã nguồn]
Diện tích mặt của ellipsoid được tính bởi:
trong đó
- (dạng dẹt), hoặc (dạng dài), là góc modular, hay độ lệch tâm góc
- và , là các tích phân elip chưa hoàn thành bậc nhất và bậc hai.
Một công thức gần đúng là:
trong đó p ≈ 1.6075 với sai số không vượt quá 1.061% (Công thức Knud Thomsen); một giá trị của p = 8/5 = 1.6 là tối ưu cho các ellipsoid gần với hình cầu, với sai số nhiều nhất 1.178% (Công thức David W. Cantrell).
Công thức chính xác bao gồm cả công thức cho trường hợp a = b (nghĩa là một phỏng cầu):
- Với dạng dẹt:
- Với dạng dài:
Trong trường hợp "gần phẳng" , diện tích này xấp xỉ
Khối lượng[sửa | sửa mã nguồn]
Khối lượng của một ellipsoid với mật độ đều là:
trong đó là mật độ.
Khối lượng moment quán tính của một ellipsoid mật độ đều là:
trong đó , , và là môment quán tính tương ứng theo trục x, y, và z. Tích của các mô men quán tính bằng 0.
Nếu a=b=c, đó là môment quán tính của hình cầu đồng chất.
Phép biến đổi tuyến tính[sửa | sửa mã nguồn]
Khi áp dụng một phép biến đổi tuyến tính khả nghịch vào một mặt cầu ta nhận được một ellipsoid. Giao của một ellipsoid với một mặt phẳng có thể là rỗng, là một điểm hoặc một đường elip. Người ta cũng định nghĩa các ellipsoid với số chiều lớn hơn như là ảnh của một mặt cầu qua một phép biến đổi tuyến tính khả nghịch.
Hình trứng[sửa | sửa mã nguồn]
Quả trứng gà có khoảng một nửa là hình khum và nửa kia là hình khối ellipsoid gần cầu (có thể hơi dẹt) nối vào xích đạo, chia sẻ trục chính của đối xứng quay. Tuy thuật ngữ hình trứng thường ngụ ý không có đối xứng gập đôi qua mặt xích đạo, nhưng nó cũng có thể chỉ đến những ellipsoid hình khum thật. Nó cũng có thể miêu tả hình 2D mà khi được xoay quanh trục chính, định ra mặt 3D. Xem thêm hình trái xoan.
Xem thêm[sửa | sửa mã nguồn]
- Phỏng cầu
- Paraboloid
- Hyperboloid
- Ellipsoid chuẩn
- Geoid
- Phương pháp ellipsoid
- Superellipsoid
- (136108) 2003 EL61, tiểu hành tinh hình ellipsoid
Tham khảo[sửa | sửa mã nguồn]
![]() Tư liệu liên quan tới Ellipsoids tại Wikimedia Commons
Tư liệu liên quan tới Ellipsoids tại Wikimedia Commons

































