Cây splay
| Cây splay | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kiểu | cây | ||||||||||||||||||||
| Phát minh năm | 1985 | ||||||||||||||||||||
| Phát minh bởi | Daniel Dominic Sleator và Robert Endre Tarjan | ||||||||||||||||||||
| Độ phức tạp thời gian theo ký hiệu O lớn | |||||||||||||||||||||
| |||||||||||||||||||||
Cây splay là một cây tìm kiếm nhị phân tự cân bằng. Nó có thực hiện các thao tác cơ bản như chèn, tìm, và xóa trong thời gian trừ dần O(log n). Với nhiều dãy thao tác không ngẫu nhiên, cây splay chạy nhanh hơn các loại cây tìm kiếm nhị phân khác ngay cả khi dãy thao tác không được biết trước. Cây splay được Daniel Dominic Sleator và Robert Endre Tarjan phát minh năm 1985.[1]
Mọi thao tác trên cây đều dựa trên một thao tác cơ bản gọi là splay (mở rộng). Khi thực hiện thao tác splay trên một nút của cây, cây được sắp xếp lại sao cho nút đó nằm ở gốc của cây. Một cách để thực hiện thao tác đó là trước hết tìm kiếm nút trên cây như cây nhị phân thông thường rồi thực hiện một chuỗi các phép quay cây theo một cách nhất định để đưa nút đó lên gốc. Thay vào đó, cũng có thể dùng một thuật toán từ trên xuống dưới kết hợp tìm kiếm và quay ngay trong quá trình tìm.
Ưu điểm[sửa | sửa mã nguồn]
Việc cây splay thực hiện nhanh chóng các thao tác là dựa trên tính tự tối ưu hóa của cây theo đó các nút hay được truy cập được di chuyển lại gần với gốc. Chiều cao xấu nhất là O(n) nhưng điều này rất hiếm khi xảy ra, và chiều cao trung bình là O(log n). Việc các nút hay sử dụng nằm ở gần gốc của cây là một ưu điểm lớn cho nhiều ứng dụng thực tế như các thuật toán cho bộ nhớ đệm và dọn rác.
Các ưu điểm bao gồm:
- Lập trình đơn giản hơn nhiều loại cây nhị phân cân bằng khác như cây đỏ đen và cây AVL.
- Tốc độ trung bình ngang với các cây khác.[cần dẫn nguồn]
- Tốn ít bộ nhớ do không phải lưu trữ thêm thông tin để cân bằng cây.
Nhược điểm[sửa | sửa mã nguồn]
Một nhược điểm của cây splay là chiều cao của cây có thể là tuyến tính. Chẳng hạn, trường hợp này xảy ra khi truy cập lần lượt n phần tử của cây theo thứ tự tăng dần. Do chiều cao tương ứng với thời gian tìm kiếm, thời gian tìm kiếm trong trường hợp xấu nhất cũng là tuyến tính. Tuy nhiên cũng cần ghi chú là chi phí trừ dần trong trường hợp xấu nhất là O(log n).
Cây splay thay đổi cấu trúc rất nhiều ngay cả khi thực hiện thao tác tìm kiếm (trong khi chẳng hạn, cây đỏ đen không thực hiện thay đổi nào khi tìm kiếm). Điều này khiến việc sử dụng cây splay trong môi trường đa luồng rất phức tạp và kém hiệu quả hơn các cây khác.
Các thao tác[sửa | sửa mã nguồn]
Splay[sửa | sửa mã nguồn]
Khi truy cập một nút x, ta thực hiện thao tác splay trên nút x để chuyển nó về vị trí gốc. Thao tác splay bao gồm nhiều bước splay, mỗi bước di chuyển x về gần gốc hơn. Việc luôn luôn thực hiện splay trên nút vừa được truy cập khiến các nút mới truy cập nằm gần gốc và cây luôn giữ hình dạng gần cân bằng.
Mỗi bước splay phụ thuộc vào ba yếu tố:
- x là nút con trái hay phải của cha nó là p,
- p có là nút gốc hay không, và nếu không thì
- p là nút con trái hay phải của cha nó là g.
Sau mỗi bước splay nút cha của g là gg phải cập nhật để trỏ tới x. Nếu gg không tồn tại thì x là nút gốc mới.
Mỗi bước splay thuộc một trong ba kiểu sau:
Bước zig: Thực hiện bước này nếu p là gốc. Cây được quay trên cạnh nối x và p. Chỉ cần thực hiện phép zig khi x ở độ sâu lẻ khi thao tác splay bắt đầu.

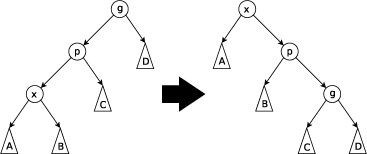
Bước zig-zig: Thực hiện bước này khi p không là gốc và x và p đều là nút con trái hoặc đều là nút con phải. Ảnh dưới là cho trường hợp x và p đều là nút con trái (trường hợp kia hoàn toàn đối xứng). Cây quay trên cạnh nối p và cha nó là g, sau đó quay trên cạnh nối x và p. Ghi chú đây là bước duy nhất khác với phương pháp quay về gốc của Allen và Munro[2] đã được tìm ra trước cây splay.
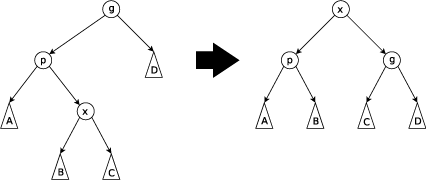
Bước zig-zag: Thực hiện bước này khi p không là gốc và x là nút con phải và p là nút con trái hoặc ngược lại. Cây quay trên cạnh nối x và p, rồi quay trên cạnh nối x và nút cha mới là g.
Chèn[sửa | sửa mã nguồn]
Để chèn x vào cây:
- Đầu tiên chèn như cây tìm kiếm nhị phân thông thường.
- Thực hiện thao tác splay trên x để đưa nó về gốc.
Xóa[sửa | sửa mã nguồn]
Để xóa x, ta dùng phương pháp như cho cây nhị phân thông thường: nếu x có hai con, đổi chỗ x và nút phải nhất của cây con trái của x hoặc nút trái nhất của cây con phải của x. Sau đó xóa nút x ở vị trí mới. Bằng phương pháp này, ta luôn đưa về trường hợp xóa nút với 0 hoặc 1 nút con.
Không như cây nhị phân thông thường, sau khi xóa xong, ta thực hiện thao tác splay trên nút cha của nút mới được xóa.
HOẶC
Trước tiên thực hiện splay để đưa nút cần xóa về gốc rồi xóa. Sau đó cây bị chia cắt thành hai cây rời nhau. Thực hiện phép splay trên nút phải nhất của cây trái (cách 1), hoặc nút trái nhất của cây phải (cách 2) để đưa nó về gốc. Trong cách 1, nối cây phải vào làm cây con phải của nút gốc mới của cây trái. Nút gốc của cây trái trở thành nút gốc của cây mới hợp lại.
Đảm bảo của cây splay[sửa | sửa mã nguồn]
Có nhiều định lý và giả thuyết về thời gian chạy của cây splay trên dãy S gồm m thao tác tìm kiếm trên cây chứa n phần tử.
- Định lý cân bằng[1]
- Thời gian thực hiện dãy S là Nói cách khác, cây splay thực hiện tốt ngang với cây tìm kiếm nhị phân cân bằng tĩnh trên dãy gồm ít nhất n thao tác tìm.
- Định lý tối ưu tĩnh[1]
- Đặt là số lần tìm phần tử i trong dãy S. Thời gian thực hiện S là Nói cách khác cây splay thực hiện tốt ngang với cây tìm kiếm nhị phân tĩnh tối ưu trên dãy gồm ít nhất n thao tác tìm.
- Định lý ngón trỏ tĩnh[1]
- Đặt là phần tử được tìm ở thao tác thứ của S và đặt f là một phần tử cố định (ngón trỏ). Thời gian thực hiện S là
- Định lý tập hợp đang hoạt động[1]
- Đặt là số phần tử khác nhau được tìm kiếm giữa thao tác thứ j và lần gần nhất trước đó được tìm. Thời gian thực hiện S là
- Định lý ngón trỏ động[3][4]
- Thời gian thực hiện S là
- Định lý quét[5]
- Còn gọi là định lý truy cập tuần tự. Tìm kiếm n phần tử của cây splay theo thứ tự tăng dần mất thời gian O(n), bất kể hình dạng ban đầu của cây là thế nào. Chặn trên chặt nhất cho tới nay là .[6]
Tham khảo[sửa | sửa mã nguồn]
- ^ a b c d e Sleator, Daniel D.; Tarjan, Robert E. (1985), “Self-Adjusting Binary Search Trees” (PDF), Journal of the ACM (Association for Computing Machinery), 32 (3): 652–686, doi:10.1145/3828.3835
- ^ Allen, Brian; and Munro, Ian (1978), “Self-organizing search trees”, Journal of the ACM, 25 (4): 526–535, doi:10.1145/322092.322094Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
- ^ Cole, Richard (2000), Mishra, Bud; Schmidt, Jeanette; and Siegel, Alan, “On the Dynamic Finger Conjecture for Splay Trees. Part I: Splay Sorting log n-Block Sequences”, SIAM (Society for Industrial and Applied Mathematics) Journal on Computing, 30: 1–43
- ^ Cole, Richard (2000), “On the Dynamic Finger Conjecture for Splay Trees. Part II: The Proof”, SIAM Journal on Computing, 30: 44–85, doi:10.1137/S009753979732699X
- ^ Tarjan, Robert E. (1985), “Sequential access in splay trees takes linear time”, Combinatorica, 5 (4): 367–378, doi:10.1007/BF02579253
- ^ Elmasry, Amr (2004), “On the sequential access theorem and Deque conjecture for splay trees”, Theoretical Computer Science, 314 (3): 459–466, doi:10.1016/j.tcs.2004.01.019










