Mô hình bài toán xác định tương tác trao đổi Tương tác trao đổi là một hiệu ứng lượng tử xảy ra khi hàm sóng của hai hay nhiều điện tử phủ nhau, có tác dụng làm tăng hay giảm năng lượng tự do của hệ, làm cho các spin song song hoặc đối song song với nhau. Về mặt bản chất, tương tác trao đổi là tương tác tĩnh điện đặc biệt giữa các spin . Hiệu ứng này được phát hiện một cách độc lập bởi Werner Heisenberg [1] Paul Dirac [2] 1926 .
Mô hình tương tác trao đổi [ sửa | sửa mã nguồn ] Mô hình tương tác trao đổi được Heisenberg và Dirac đề xuất, London là người phát triển và đưa ra mô hình tính toán dựa trên mẫu đơn giản về nguyên tử hydro với hai nguyên tử đặt cạnh nhau (hình vẽ) và lúc đó phương trình Schrodinger được viết bởi:
[
Δ
1
+
Δ
2
+
ℏ
2
2
m
[
E
−
V
(
R
,
r
a
1
,
r
a
2
,
r
b
1
,
r
b
2
,
r
)
]
ψ
=
0
{\displaystyle [\Delta _{1}+\Delta _{2}+{\frac {\hbar ^{2}}{2m}}[E-V(R,r_{a1},r_{a2},r_{b1},r_{b2},r)]\psi =0}
với
Δ
1
,
Δ
2
{\displaystyle \Delta _{1},\Delta _{2}}
toán tử động năng của 2 điện tử ,
E
{\displaystyle E}
V
{\displaystyle V}
thế năng .
Δ
1
=
∂
2
∂
x
1
2
+
∂
2
∂
y
1
2
+
∂
2
∂
z
1
2
{\displaystyle \Delta _{1}={\frac {\partial ^{2}}{\partial x_{1}^{2}}}+{\frac {\partial ^{2}}{\partial y_{1}^{2}}}+{\frac {\partial ^{2}}{\partial z_{1}^{2}}}}
Δ
2
=
∂
2
∂
x
2
2
+
∂
2
∂
y
2
2
+
∂
2
∂
z
2
2
{\displaystyle \Delta _{2}={\frac {\partial ^{2}}{\partial x_{2}^{2}}}+{\frac {\partial ^{2}}{\partial y_{2}^{2}}}+{\frac {\partial ^{2}}{\partial z_{2}^{2}}}}
V
=
e
2
R
+
e
2
r
−
e
2
r
a
1
−
e
2
r
a
2
−
e
2
r
b
1
−
e
2
r
b
2
{\displaystyle V={\frac {e^{2}}{R}}+{\frac {e^{2}}{r}}-{\frac {e^{2}}{r_{a1}}}-{\frac {e^{2}}{r_{a2}}}-{\frac {e^{2}}{r_{b1}}}-{\frac {e^{2}}{r_{b2}}}}
ψ
=
ψ
(
q
1
,
q
2
)
=
ψ
(
x
1
,
y
1
,
z
1
,
x
2
,
y
2
,
z
2
)
{\displaystyle \psi =\psi (q_{1},q_{2})=\psi (x_{1},y_{1},z_{1},x_{2},y_{2},z_{2})}
Bài toán được giải bằng phương pháp gần đúng liên tục theo nguyên tắc:
[
Δ
1
+
ℏ
2
2
m
(
E
0
−
e
2
r
a
1
)
]
ψ
a
(
q
1
)
=
0
{\displaystyle [\Delta _{1}+{\frac {\hbar ^{2}}{2m}}(E_{0}-{\frac {e^{2}}{r_{a1}}})]\psi _{a}(q_{1})=0}
với
E
0
{\displaystyle E_{0}}
ψ
0
(
q
1
,
q
2
)
=
α
ψ
a
(
q
1
)
ψ
b
(
q
2
)
+
β
ψ
b
(
q
1
)
ψ
a
(
q
2
)
{\displaystyle \psi _{0}(q_{1},q_{2})=\alpha \psi _{a}(q_{1})\psi _{b}(q_{2})+\beta \psi _{b}(q_{1})\psi _{a}(q_{2})}
α
,
β
{\displaystyle \alpha ,\beta }
tuyến tính .
Đưa hai nguyên tử lại khoảng cách gần nhau, và ta có gần đúng bậc nhất . Lúc đó, do sự tương tác giữa các điện tử và iôn , năng lượng của hệ được thay bởi:
E
=
2
E
0
+
E
′
{\displaystyle E=2E_{0}+E'}
Lúc đó, nghiệm tổng quát của bài toán có thể thay đổi:
α
(
E
′
−
e
2
R
−
e
2
r
+
e
2
r
a
1
+
e
2
r
b
1
)
ψ
a
(
q
1
)
ψ
b
(
q
2
)
+
β
(
E
′
−
e
2
R
−
e
2
r
+
e
2
r
a
2
+
e
2
r
b
2
)
ψ
b
(
q
1
)
ψ
a
(
q
2
)
=
0
{\displaystyle \alpha (E'-{\frac {e^{2}}{R}}-{\frac {e^{2}}{r}}+{\frac {e^{2}}{r_{a1}}}+{\frac {e^{2}}{r_{b1}}})\psi _{a}(q_{1})\psi _{b}(q_{2})+\beta (E'-{\frac {e^{2}}{R}}-{\frac {e^{2}}{r}}+{\frac {e^{2}}{r_{a2}}}+{\frac {e^{2}}{r_{b2}}})\psi _{b}(q_{1})\psi _{a}(q_{2})=0}
∫
ψ
a
∗
(
q
)
ψ
b
(
q
)
d
q
=
0
{\displaystyle \int \psi _{a}^{*}(q)\psi _{b}(q)dq=0}
Nếu ta đặt:
C
=
e
2
R
+
∫
(
e
2
r
−
e
2
r
b
1
−
e
2
r
a
2
)
|
ψ
a
(
q
1
)
|
2
|
ψ
b
(
q
2
)
|
2
d
q
1
d
q
2
{\displaystyle C={\frac {e^{2}}{R}}+\int ({\frac {e^{2}}{r}}-{\frac {e^{2}}{r_{b1}}}-{\frac {e^{2}}{r_{a2}}})|\psi _{a}(q_{1})|^{2}|\psi _{b}(q_{2})|^{2}dq_{1}dq_{2}}
A
=
∫
(
e
2
r
−
e
2
r
a
1
−
e
2
r
b
2
)
ψ
a
∗
(
q
1
)
ψ
b
(
q
1
)
ψ
b
∗
(
q
2
)
ψ
a
(
q
2
)
d
q
1
d
q
2
{\displaystyle A=\int ({\frac {e^{2}}{r}}-{\frac {e^{2}}{r_{a1}}}-{\frac {e^{2}}{r_{b2}}})\psi _{a}^{*}(q_{1})\psi _{b}(q_{1})\psi _{b}^{*}(q_{2})\psi _{a}(q_{2})dq_{1}dq_{2}}
Bài toán có thể viết đơn giản thành:
α
(
E
′
−
C
)
−
β
A
=
0
{\displaystyle \alpha (E'-C)-\beta A=0}
và
α
A
−
β
(
E
′
−
C
)
=
0
{\displaystyle \alpha A-\beta (E'-C)=0}
và có thể rút ra năng lượng:
E
′
=
C
±
A
{\displaystyle E'=C\pm A}
E
=
2
E
0
+
C
±
A
{\displaystyle E=2E_{0}+C\pm A}
Hệ số
A
{\displaystyle A}
tích phân trao đổi của hệ, được viết tổng quát như sau:
A
i
j
=
∫
ψ
a
∗
(
q
)
ψ
j
∗
(
q
)
ψ
i
(
q
′
)
ψ
j
(
q
′
)
[
V
i
j
(
|
q
−
q
′
|
)
+
g
i
(
q
)
+
g
j
(
q
)
]
d
q
d
q
′
{\displaystyle A_{ij}=\int \psi _{a}^{*}(q)\psi _{j}^{*}(q)\psi _{i}(q')\psi _{j}(q')[V_{ij}(|q-q'|)+g_{i}(q)+g_{j}(q)]dqdq'}
Tương tác trao đổi và tiêu chuẩn sắt từ [ sửa | sửa mã nguồn ] Khi áp dụng mô hình tương tác trao đổi trong mẫu sắt từ, năng lượng của hệ các spin (năng lượng tương tác trao đổi) được viết bởi:
W
e
x
=
−
2
∑
i
,
j
A
i
j
(
σ
j
→
.
σ
j
→
)
{\displaystyle W_{ex}=-2\sum _{i,j}A_{ij}({\vec {\sigma _{j}}}.{\vec {\sigma _{j}}})}
với
A
i
j
{\displaystyle A_{ij}}
σ
i
→
,
σ
j
→
{\displaystyle {\vec {\sigma _{i}}},{\vec {\sigma _{j}}}}
Như vậy, để cực tiểu hóa năng lượng thì 2 spin cạnh nhau phải hoàn toàn song song với nhau.
Với giá trị
A
i
j
>
0
{\displaystyle A_{ij}>0}
sắt từ (tương tác trao đổi dương), nếu
A
i
j
<
0
{\displaystyle A_{ij}<0}
phản sắt từ .
Tương tác trao đổi gián tiếp [ sửa | sửa mã nguồn ] Trong một số vật liệu đặc biệt (điển hình là các perovskite ) thì từ tính được tạo ra không trực tiếp từ các spin liên kết trực tiếp với nhau mà xảy ra một cách gián tiếp, có nghĩa là, tương tác trao đổi cũng được tạo ra một cách gián tiếp giữa các iôn thông qua iôn O2+ .
Các điện tử trên mức
e
g
{\displaystyle e_{g}}
iôn O2+ mà vẫn giữ nguyên hướng spin sao cho phù hợp với quy tắc Hund . Đây là cơ chế liên kết gián tiếp giữa hai iôn thông qua O2+ .
Nếu 2 iôn cùng hóa trị (ví dụ Mn4+ với Mn4+ ), tương tác trao đổi sẽ là âm, ta có tương tác siêu trao đổi tạo ra tính phản sắt từ .
Trong trường hợp 2 iôn khác hóa trị (ví dụ Mn4+ với Mn3+ ) ta sẽ có tương tác trao đổi kép tạo ra tính sắt từ .
Cường độ tương tác trao đổi gián tiếp phụ thuộc vào 2 yếu tố:
Độ dài liên kết: Mn-O
Góc liên kết Mn-O-Mn 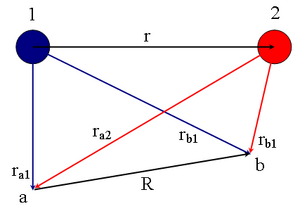

![{\displaystyle [\Delta _{1}+\Delta _{2}+{\frac {\hbar ^{2}}{2m}}[E-V(R,r_{a1},r_{a2},r_{b1},r_{b2},r)]\psi =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79af290c0d85ed7cb2ee932f2cfe36579d803c20)







![{\displaystyle [\Delta _{1}+{\frac {\hbar ^{2}}{2m}}(E_{0}-{\frac {e^{2}}{r_{a1}}})]\psi _{a}(q_{1})=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e55efbc4c65c3d1bb85ffedc1a2295fc8189617)













![{\displaystyle A_{ij}=\int \psi _{a}^{*}(q)\psi _{j}^{*}(q)\psi _{i}(q')\psi _{j}(q')[V_{ij}(|q-q'|)+g_{i}(q)+g_{j}(q)]dqdq'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d06eefdd245c72fb7525209bbc452fc8265c3ec)





