Thuật toán khóa đối xứng
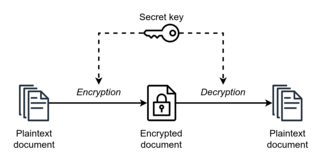
Trong mật mã học, các thuật toán khóa đối xứng (tiếng Anh: symmetric-key algorithms) là một lớp các thuật toán mật mã hóa trong đó các khóa dùng cho việc mật mã hóa và giải mã có quan hệ rõ ràng với nhau (có thể dễ dàng tìm được một khóa nếu biết khóa kia). Mã khóa loại này không công khai.
Khóa dùng để mã hóa có liên hệ một cách rõ ràng với khóa dùng để giải mã có nghĩa chúng có thể hoàn toàn giống nhau, hoặc chỉ khác nhau nhờ một biến đổi đơn giản giữa hai khóa. Trên thực tế, các khóa này đại diện cho một bí mật được phân hưởng bởi hai bên hoặc nhiều hơn và được sử dụng để giữ gìn sự bí mật trong kênh truyền thông tin.
Nhiều thuật ngữ khác dành cho việc mã hóa dùng chìa khóa đối xứng bao gồm các phương pháp mã hóa đơn khóa (single-key), phương pháp mã hóa một khóa (one-key) và phương pháp mã hóa khóa cá nhân (private-key). Cách sử dụng thuật ngữ sau cùng đôi khi gây xung đột với thuật ngữ khóa cá nhân (private-key) dùng trong mật mã hóa khóa công khai (public key cryptography).
Các loại thuật toán khóa đối xứng[sửa | sửa mã nguồn]
Thuật toán đối xứng có thể được chia ra làm hai thể loại, mật mã luồng (stream ciphers) và mật mã khối (block ciphers). Mật mã luồng mã hóa từng bit của thông điệp trong khi mật mã khối gộp một số bit lại và mật mã hóa chúng như một đơn vị. Cỡ khối được dùng thường là các khối 64 bit. Thuật toán tiêu chuẩn mã hóa tân tiến (Advanced Encryption Standard), được NIST công nhận tháng 12 năm 2001, sử dụng các khối gồm 128 bit.
Các thuật toán đối xứng thường không được sử dụng độc lập. Trong thiết kế của các hệ thống mật mã hiện đại, cả hai thuật toán bất đối xứng (asymmetric) (dùng chìa khóa công khai) và thuật toán đối xứng được sử dụng phối hợp để tận dụng các ưu điểm của cả hai. Những hệ thống sử dụng cả hai thuật toán bao gồm những cái như SSL (Secure Sockets Layer), PGP (Pretty Good Privacy) và GPG (GNU Privacy Guard) v.v. Các thuật toán chìa khóa bất đối xứng được sử dụng để phân phối chìa khóa mật cho thuật toán đối xứng có tốc độ cao hơn.
Một số ví dụ các thuật toán đối xứng nổi tiếng và khá được tôn trọng bao gồm Twofish, Serpent, AES (còn được gọi là Rijndael), Blowfish, CAST5, RC4, Tam phần DES (Triple DES), và IDEA (International Data Encryption Algorithm - Thuật toán mật mã hóa dữ liệu quốc tế).
Tốc độ[sửa | sửa mã nguồn]
Các thuật toán đối xứng nói chung đòi hỏi công suất tính toán ít hơn các thuật toán khóa bất đối xứng (asymmetric key algorithms). Trên thực tế, một thuật toán khóa bất đối xứng có khối lượng tính toán nhiều hơn gấp hằng trăm, hằng ngàn lần một thuật toán khóa đối xứng (symmetric key algorithm) có chất lượng tương đương.
Những hạn chế[sửa | sửa mã nguồn]
Hạn chế của các thuật toán khóa đối xứng bắt nguồn từ yêu cầu về sự phân hưởng chìa khóa bí mật, mỗi bên phải có một bản sao của chìa. Do khả năng các chìa khóa có thể bị phát hiện bởi đối thủ mật mã, chúng thường phải được bảo an trong khi phân phối và trong khi dùng. Hậu quả của yêu cầu về việc lựa chọn, phân phối và lưu trữ các chìa khóa một cách không có lỗi, không bị mất mát là một việc làm khó khăn, khó có thể đạt được một cách đáng tin cậy.
Để đảm bảo giao thông liên lạc an toàn cho tất cả mọi người trong một nhóm gồm n người, tổng số lượng chìa khóa cần phải có là [1].
Hiện nay người ta phổ biến dùng các thuật toán bất đối xứng có tốc độ chậm hơn để phân phối chìa khóa đối xứng khi một phiên giao dịch bắt đầu, sau đó các thuật toán khóa đối xứng tiếp quản phần còn lại (xem Bảo an tầng giao vận (Transport Layer Security)). Vấn đề về bảo quản sự phân phối chìa khóa một cách đáng tin cậy cũng tồn tại ở tầng đối xứng, song ở một điểm nào đấy, người ta có thể kiểm soát chúng dễ dàng hơn. Tuy thế, các khóa đối xứng hầu như đều được sinh tạo tại chỗ.
Các thuật toán khóa đối xứng không thể dùng cho mục đích xác thực (authentication) hay mục đích chống thoái thác (non-repudiation) được.
Tính thuận nghịch[sửa | sửa mã nguồn]
Theo định nghĩa, các hàm số dùng trong mật mã học phải có khả năng đảo ngược (reversible), vì chúng ta cần phải có khả năng vừa mật mã hóa các thông điệp song cũng đồng thời giải mã chúng (với điều kiện chúng ta có chìa khóa đúng của nó).
Trong quá khứ, nhiều phương pháp đã được sử dụng để giải quyết việc này. Trước đây, người ta đã từng dùng sách mật mã - trong đó chìa khóa phân hưởng liên quan đến nội dụng của quyển sách, mật mã khóa tự động - trong đó chìa khóa có thể được suy ra từ một phần của văn bản thuần túy (plaintext), mã đục lỗ (grill) (Có giả thuyết rằng phương pháp này đầu tiên được nhà toán học người Ý Gerolamo Cardano sáng chế)[2], vân vân. Trong thời đại hiện nay, khi máy tính trở nên sẵn có, đa số các phương pháp mật mã đối xứng đều dựa trên cơ sở 'vòng' tuần hoàn (các lượt tính toán được nhắc đi nhắc lại). Thường thì một lượt được nhắc đi nhắc lại nhiều lần, theo một sự bố trí khá đơn giản, như trong ví dụ chung dưới đây. Phương pháp chung này thường được gán cho ông Horst Feistel. Để biết được nội dung có chiều sâu hơn nữa về phương pháp này (với biểu đồ minh họa), xin xem bài về Feistel cipher.
Những bit dùng để mã hóa được phân ra là hai phần, P1 và P2. P1 được giữ nguyên, không thay đổi, P2 được cộng (hay được XOR) với một hàm băm một chiều (one-way hashed function) f (được biến thiên bởi một chìa khóa hay một nhân tố (salt)) của P1. Hai kết quả này sau đó được đổi chỗ cho nhau. Mỗi quá trình này được gọi là 'một lượt' (hay một vòng).
Chẳng hạn với p1, p2, chìa khóa là các vectơ bit; Dấu phẩy (',') là toán tử phép ghép chuỗi và f là ánh xạ từ hầu cho:
(key = chìa khóa)
Vì kết quả của lượt tính này vẫn còn cho phép truy cập giá trị của P1, và tính cộng là một phép toán có thể đảo ngược được, cho nên phép toán có thể được hoàn giải, đối với bất cứ một hàm số f nào đấy.
Tuy đã kinh qua một vòng toán, song kết quả của nó vẫn chưa được an toàn cho lắm, vì p1 vẫn còn giữ nguyên giá trị và chưa bị thay đổi, nhưng nếu chúng ta lặp lại phép toán một hoặc nhiều lần, thường là bởi nhiều hàm số khác và với 'các chìa khóa của vòng toán' ('round keys'), thì kết quả sẽ tăng cường tính đảm bảo của nó rất nhiều (greatly improves the strength).
Để giải mã bội số lượt, mỗi lượt phải được giải theo trật tự ngược lại và vì thế, trong khi giải mã, các chìa khóa cũng phải được áp dụng theo trật tự ngược lại.
Sau nhiều lần (đa số là từ 8 đến 64 lần) thi hành, kết quả trở nên bị xáo trộn đến mức, như trong trường hợp khi các mã được thiết kế khá tốt, không có phương pháp giải mã nào nhanh hơn là phương pháp tìm khóa dùng bạo lực (brute force key search)[3] và chỉ có phương pháp này mới có thể giải được.
Tấn công đối với các mật mã đối xứng[sửa | sửa mã nguồn]
Trong quá khứ, các mã đối xứng thường rất dễ bị ảnh hưởng bởi các loại tấn công gọi là tấn công với văn bản thuần túy biết trước (known-plaintext attacks), tấn công với văn bản thuần túy chọn trước (chosen plaintext attacks), thám mã vi phân (differential cryptanalysis) và thám mã tuyến tính (linear cryptanalysis). Nếu mỗi hàm số sử dụng trong các vòng toán được thiết kế một cách cẩn thận, thì nó sẽ giảm khả năng chìa khóa của mã bị tấn công một cách thành công rất nhiều.
Khi được sử dụng với mật mã đối xứng để truyền tin chìa khóa mật mã, các trình sinh tạo chìa khóa giả ngẫu nhiên (pseudorandom key generators) thường được sử dụng để sinh tạo các chìa khóa dùng trong phiên giao dịch sử dụng mật mã đối xứng. Song trong quá khứ, sự thiếu hụt trong tính ngẫu nhiên của các trình sinh tạo ngẫu số[4] hay trong các vectơ khởi tạo (initialization vectors) của chúng thường gây ra những thảm họa và thường dẫn đến các vụ mật mã bị bẻ gãy. Việc thực hiện và triển khai thận trọng, với khởi tạo (initialization) dựa trên những nguồn entrôpi có chất lượng cao là một yếu tố cần thiết để thuyên giảm sự mất mát trong an ninh.
Ghi chú[sửa | sửa mã nguồn]
- ^ Beutelspacher, Albrecht (1994). “The Future Has Already Started or Public Key Cryptography (Tương lai đã bắt đầu hay Mật mã dùng khóa công khai)”. Cryptology. bản dịch từ tiếng Đức do J. Chris Fisher dịch. tr. 102. ISBN 0-88385-504-6.
- ^ Mã đục lỗ (tiếng Anh: Grill hay grille) - là một phương pháp mật mã cổ xưa, trong đó, người muốn gửi một thông điệp mật mã lấy một miếng bìa rồi đục các lỗ ở nhiều vị trí khác nhau, mỗi lỗ là vị trí của một chữ trong thông điệp mật mã. Những khoảng trống giữa các chữ trong thông điệp mật sau đó được điền thêm vào và biến nó thành một bức thư thông thường. Mã đục lỗ đã được chứng minh là một phương pháp mật mã khó giải, trừ phi người giải mã có cùng một miếng bìa với các vị trí lỗ tương tự như miếng bìa của người viết mật mã. Do bị đục thành nhiều lỗ, miếng bìa trông giống một lưới sắt - như cái lưới sắt dùng để kẹp và nướng chả nên người ta gọi nó là grill, hay lưới sắt. Có nơi Lưu trữ 2006-09-08 tại Wayback Machine nói rằng mật mã đục lỗ được sáng chế bởi Cardinal Richelieu vào khoảng 1600.
- ^ Từ brute force trong tiếng Anh tuy được dịch là bạo lực, song phương pháp dùng bạo lực ở đây ám chỉ đến phương pháp kiểm tra tất cả các tổ hợp của chìa khóa, không ngoại trừ một khả năng nào. Việc tấn công này thường được dùng kèm với một từ điển. Một số mạng tiếng Việt có dịch từ brute force attack là tấn công vét cạn. Tuy thô tục, song nó diễn tả được phần nào đặc tính của hoạt động.
- ^ Trình sinh tạo ngẫu số giả (tiếng Anh: pseudorandom generators) là những thuật toán nhằm bắt chước những quá trình sinh tạo ngẫu số tự nhiên - một quá trình sinh tạo các ngẫu số không lặp lại và không theo một quy luật biết trước nào hết - không tạo nên các ngẫu số tự nhiên và người ta có thể đoán được số tiếp theo là gì nếu biết được công thức của thuật toán.
Liên kết ngoài[sửa | sửa mã nguồn]
- Crypto-Toolbox - Online cryptography, hashing and PIN block sanity checking for EftPos developers.



