Phát xạ kích thích

Trong quang học, phát xạ kích thích hay còn gọi là phát xạ cảm ứng là quá trình mà một electron của nguyên tử (hoặc một phân tử) ở trạng thái kích thích tương tác với sóng điện từ có tần số nhất định có thể giải phóng năng lượng của nó vào trường điện từ và nhảy xuống mức năng lượng thấp hơn. Một photon được tạo ra theo cách này có cùng pha, tần số, phân cực, và hướng như các photon của sóng tới. Điều này trái ngược với phát xạ tự phát xảy ra khi không có trường điện từ xung quanh. Tuy nhiên, quá trình này lại tương tự như quá trình hấp thụ của nguyên tử, tức là quá trình mà năng lượng của một photon được hấp thụ gây ra một sự chuyển đổi năng lượng nguyên tử, giống hệt nhau nhưng ngược lại: từ mức thấp lên mức năng lượng cao hơn.
Lý thuyết của phát xạ kích thích được Einstein khám phá[1] thuộc lĩnh vực cơ học lượng tử, trong đó năng lượng phát ra được mô tả bằng các thuật ngữ của photon, gọi là lượng tử của trường điện từ. Phát xạ kích thích cũng có thể được mô tả một cách cổ điển, tuy nhiên không liên quan đến photon hay cơ học lượng tử của vật chất.[2]
Tổng quan[sửa | sửa mã nguồn]
Electron và cách chúng tương tác với trường điện từ rất quan trọng trong nghiên cứu về hóa học và vật lý. Trong điện từ học cổ điển, năng lượng của một electron có quỹ đạo quay xung quanh hạt nhân nguyên tử nhỏ hơn năng lượng của các electron có quỹ đạo xa hạt nhân hơn. Tuy nhiên, các hiệu ứng của cơ học lượng tử có thể kích thích các electron nhảy sang các quỹ đạo nguyên tử khác. Do đó, các electron được tìm thấy đạt những mức năng lượng đặc trưng của một nguyên tử, hai trong số đó được hiển thị dưới đây:
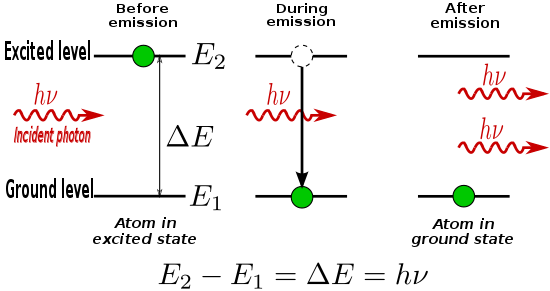
Khi một electron hấp thụ năng lượng của ánh sáng (photon) hoặc nhiệt (phonon), thì nó sẽ nhận lượng tử năng lượng tới. Nhưng quá trình chuyển đổi chỉ được phép ở giữa các mức năng lượng đặc trưng như hình trên. Điều này cho thấy sẽ thu được quang phổ vạch hấp thụ hoặc phát xạ.
Mô hình toán học[sửa | sửa mã nguồn]
Phát xạ kích thích có thể được tính toán bằng cách xem electron có thể ở một trong hai trạng thái năng lượng trong một nguyên tử: trạng thái năng lượng thấp (có thể là trạng thái cơ bản) (1) và trạng thái kích thích (2), với năng lượng E1 và E2 tương ứng.
Nếu nguyên tử ở trạng thái kích thích, nó có thể phân rã để chuyển xuống trạng thái năng lượng thấp hơn qua quá trình phát xạ tự phát, giải phóng lượng năng lượng chênh lệch giữa hai trạng thái thành một photon. Các photon sẽ có tần số ν và năng lượng hν, được cho bởi:
với h là hằng số Planck
Ngoài ra, nếu nguyên tử ở trạng thái kích thích bị tác động bởi một điện trường có tần số , nó có thể sẽ phát ra thêm một photon có cùng tần số và cùng pha, để nguyên tử trở về trạng thái năng lượng thấp hơn. Quá trình này được gọi là phát xạ kích thích.
Nếu số lượng các nguyên tử đang ở trạng thái kích thích là N2 trong tổng số nguyên tử, thì tỉ lệ xảy ra phát xạ kích thích là:
với hằng số tỷ lệ thuận B21 được gọi là hệ số Einstein, ρ(ν) là mật độ bức xạ của trường tới ở tần số ν. Vậy tỷ lệ phát xạ tỉ lệ thuận với số nguyên tử ở trạng thái kích thích và mật độ của photon tới.
Đồng thời, cùng lúc đó thì một số nguyên tử hấp thụ năng lượng của trường điện từ làm cho electron nhảy từ mức năng lượng thấp lên mức năng lượng cao hơn (tức là trong trường hợp này, electron từ mức năng lượng cơ bản nhảy lên mức năng lượng kích thích). Tỉ lệ nguyên tử hấp thụ cũng được cho bởi phương trình giống như phương trình trên:
- .
Tỉ lệ hấp thụ tỷ lệ thuận với số nguyên tử ở trạng thái thấp hơn, N1. Einstein chỉ ra rằng hệ số tỷ lệ này bằng hệ số tỷ lệ của phát xạ kích thích:
- .
Do đó quá trình hấp thụ và phát xạ kích thích là 2 quá trình đảo ngược xảy ra với những tỉ lệ khác nhau. Nếu ta xét cả một hệ gồm nhiều nguyên tử, thì 2 quá trình này có thể được xem như xảy ra cùng lúc. Tỷ lệ tổng của cả hệ chuyển đổi từ E2 về E1 bằng cách kết hợp cả hai quá trình này có thể được tính như sau:
- .
Để kết quả là một số dương, thì điều kiện là số nguyên tử bị kích thích phải lớn hơn số nguyên tử ở trạng thái năng lượng thấp hơn, tức là: . Điều kiện được gọi là đảo ngược mật độ, thường được dùng trong máy phát laser.
Tham khảo[sửa | sửa mã nguồn]
- ^ Einstein, A (1916). “Strahlungs-emission und -absorption nach der Quantentheorie”. Verhandlungen der Deutschen Physikalischen Gesellschaft. 18: 318–323. Bibcode:1916DPhyG..18..318E.
- ^ B Fain & Milonni, P (1987). “Classical stimulated emission”. JOSA B. 4 (1): 78–85.Quản lý CS1: sử dụng tham số tác giả (liên kết)
- Saleh, Bahaa E. A. and Teich, Malvin Carl (1991). Fundamentals of Photonics. New York: John Wiley & Sons. ISBN 0-471-83965-5.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
- Alan Corney (1977). Atomic and Laser Spectroscopy. Oxford: Oxford Uni. Press. ISBN 978-0199211456.
Xem thêm[sửa | sửa mã nguồn]
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Phát xạ kích thích. |








