Quang học

Quang học là một ngành của vật lý học nghiên cứu các tính chất và hoạt động của ánh sáng, bao gồm tương tác của nó với vật chất và cách chế tạo ra các dụng cụ nhằm sử dụng hoặc phát hiện nó.[1] Phạm vi của quang học thường nghiên cứu ở bước sóng khả kiến, tử ngoại, và hồng ngoại. bởi vì ánh sáng là sóng điện từ, những dạng khác của bức xạ điện từ như tia X, sóng vi ba, và sóng vô tuyến cũng thể hiện các tính chất tương tự.[1]
Hầu hết các hiện tượng và hiệu ứng quang học có thể được miêu tả phù hợp bởi điện từ học cổ điển. Tuy nhiên, cách miêu tả điện từ đầy đủ của ánh sáng lại rất khó áp dụng trong thực tiễn. Quang học thực hành thường sử dụng các mô hình đơn giản. Theo nghĩa chung nhất đó là quang hình học, ngành nghiên cứu tính chất của tia sáng khi nó lan truyền trong môi trường theo đường thẳng hoặc bị lệch hay phản xạ giữa các môi trường. Quang học vật lý là mô hình đầy đủ hơn về ánh sáng, bao gồm các hiệu ứng có bản chất sóng như nhiễu xạ và giao thoa mà không thể giải thích bởi quang hình học. Về mặt lịch sử, các nhà vật lý đã phát triển mô hình tia sáng đầu tiên, sau đó là mô hình sóng và mô hình hạt ánh sáng. Sự phát triển của lý thuyết điện từ học trong thế kỷ 19 đã dẫn tới khám phá ra rằng ánh sáng có bản chất là một loại bức xạ điện từ.
Một số hiệu ứng của ánh sáng chỉ có thể giải thích dựa trên bản chất lưỡng tính sóng hạt của ánh sáng. Cơ sở của những hiệu ứng này được miêu tả bởi cơ học lượng tử. Khi xem ánh sáng có tính chất hạt, thì ánh sáng được mô hình bởi tập hợp các hạt gọi là "photon". Quang học lượng tử là ngành ứng dụng các tính chất lượng tử để nghiên cứu các hệ quang học.
Ngành quang học có sự liên quan và ứng dụng cho nhiều lĩnh vực như thiên văn học, các lĩnh vực kỹ thuật, chụp ảnh, và y học (bao gồm nghiên cứu về mắt và đo lường thị lực). Những ứng dụng của quang học có thể thấy trong nhiều lĩnh vực công nghệ và đời sống, như gương, thấu kính, kính thiên văn, kính hiển vi, laser, và sợi quang học.
Lịch sử[sửa | sửa mã nguồn]

Quang học bắt đầu với sự phát triển thấu kính của người Ai Cập cổ đại và Lưỡng Hà. Thấu kính sớm nhất được biết tới, làm từ các tinh thể được mài bóng, thường là thạch anh, có niên đại vào khoảng năm 700 trước Công nguyên ở Assyria như thấu kính Layard/Nimrud.[2] Người La Mã và Hy Lạp cổ đại đã đổ đầy các quả cầu kính bằng nước để tạo ra thấu kính. Những cách làm này sau đó được các nhà triết học Hy Lạp và Ấn Độ phát triển thành lý thuyết ánh sáng và sự nhìn, cũng như người La Mã phát triển lý thuyết quang hình học. Từ optics xuất phát từ tiếng Hy Lạp cổ đại ὀπτική, có nghĩa là "biểu hiện, nhìn nhận".[3]
Triết học Hy Lạp chia quang học ra thành hai lý thuyết đối lập dựa trên cách miêu tả làm sao mắt con người nhìn được, "lý thuyết mắt phát ra tia sáng" và "lý thuyết mắt thu nhận tia sáng".[4] Lý thuyết mắt thu nhận tia sáng cho rằng con người nhìn thấy sự vật là do các vật phát ra những bản sao giống y hệt chúng (gọi là eidola) mà mắt người thu nhận được. Với sủng hộ của nhiều triết gia như Democritus, Epicurus, Aristotle và các môn đệ, lý thuyết này dường như đã có nét giống với lý thuyết hiện đại về thị giác, nhưng nó vẫn chỉ là các tiên đoán mà thiếu đi các thí nghiệm kiểm tra.
Plato là người đầu tiên nêu ra lý thuyết mắt người phát ra các tia sáng, lý thuyết cho rằng cảm nhận thị lực là do các tia sáng phát ra từ mắt người chiếu vào vật thể. Ông cũng bình luận về tính chẵn lẻ thông qua đối xứng gương khi miêu tả vấn đề ở trong cuốn Timaeus.[5] Vài trăm năm sau, Euclid viết cuốn sách Quang học khi ông bắt đầu liên hệ sự nhìn với môn hình học, tạo ra những cơ sở đầu tiên cho ngành quang hình học.[6] Cuốn sách của ông được viết dựa trên cơ sở của lý thuyết phát tia của Plato và Euclid còn miêu tả các quy tắc toán học của phép phối cảnh cũng như hiệu ứng khúc xạ một cách định tính, mặc dù vậy ông đặt ra nghi vấn rằng chùm tia sáng từ mắt người liệu có thể ngay lập tức làm sáng lên các vì sao chỉ trong nháy mắt.[7] Ptolemy, trong cuốn Quang học của ông đã miêu tả một lý thuyết kết hợp cả hai lý thuyết trên: các tia sáng từ mắt tạo thành một hình nón, với đỉnh nằm trong mắt, và đáy nón xác định lên trường nhìn. Các tia sáng rất nhạy với mọi vật, và chúng mang thông tin chứa hướng và khoảng cách các vật trở lại não của người quan sát. Ông tổng kết lại các kết quả của Euclid và đi đến miêu tả cách đo góc khúc xạ, mặc dù ông đã không nhận ra mối liên hệ giữa góc này với góc tới của tia sáng.[8]
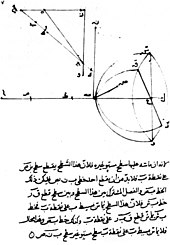
Trong thời Trung Cổ, các ý tưởng của người Hy Lạp đã được phục hồi và mở rộng trong các văn tự của thế giới Hồi giáo. Một trong những văn tự sớm nhất là của Al-Kindi (khoảng 801–73) viết về các giá trị của những ý tưởng của trường phái Aristote và Euclid về quang học, ủng hộ cho lý thuyết mắt phát tia sáng do có thể dùng nó để miêu tả định lượng các hiện tượng quang học.[9] Năm 984, nhà toán học Ba Tư Ibn Sahl viết luận thuyết "Về cách nung chảy tạo gương và thấu kính", ông đã miêu tả đúng định luật về sự khúc xạ mà có nét tương đương với định luật Snell.[10] Ông sử dụng định luật này nhằm tính toán hình dạng tối ưu cho thấu kính và các gương cầu lõm. Ở đầu thế kỷ 11, Alhazen (Ibn al-Haytham) viết cuốn Sách quang học (Kitab al-manazir) trong đó ông giải thích sự phản xạ và khúc xạ và đề xuất một hệ thống mới giải thích cho khả năng nhìn sự vật và ánh sáng dựa trên các quan sát và thực nghiệm.[11][12][13][14][15] Ông phê phán "lý thuyết phát tia sáng" của trường phái Ptolemy về mắt người phát ra tia nhìn, mà thay vào đó ông có ý tưởng về ánh sáng phản xạ theo đường thẳng ở mọi hướng từ mọi điểm của vật thể được quan sát và sau đó các tia sáng đi vào mắt, mặc dù ông không thể giải thích đúng đắn làm thế nào để mắt thu nhận được các tia sáng.[16] Công trình của Alhazen phần lớn bị lãng quên trong thế giới Ả Rập nhưng nó đã được một học giả vô danh biên dịch sang tiếng La tinh vào khoảng năm 1200 và sau này nó được thầy tu người Ba Lan Witelo tổng kết và mở rộng[17] đưa nó trở thành một cuốn sách mẫu mực về quang học ở châu Âu trong gần 400 năm tiếp theo.
Ở thế kỷ 13 giám mục người Anh Robert Grosseteste viết một tác phẩm về ánh sáng trên nhiều chủ đề khoa học dưới bốn quan điểm khác nhau: nhận thức luận về ánh sáng, lý luận siêu hình học về ánh sáng, thuyết nguyên nhân hoặc tính chất vật lý của ánh sáng, lý luận thần học về ánh sáng,[18] dựa trên các công trình của các trường phái Aristotle và Plato. Môn đệ nổi tiếng nhất của Grosseteste, Roger Bacon, đã viết những công trình với nguồn trích dẫn phong phú dựa trên các bản dịch thời đó về các nghiên cứu quang học và triết học, bao gồm của Alhazen, Aristotle, Avicenna, Averroes, Euclid, al-Kindi, Ptolemy, Tideus, và Constantine the African. Bacon đã dùng các phần của một khối cầu thủy tinh để làm kính lúp để chứng tỏ ánh sáng phản xạ từ vật thể hơn là phát ra từ chúng.
Kính mắt đầu tiên được phát minh vào khoảng năm 1286 ở Ý.[19] Điều này dẫn tới sự ra đời của ngành công nghiệp quang học với mục đích mài cắt và đánh bóng thấu kính để làm các kính mắt, lúc đầu là ở Venice và Florence vào thế kỷ 13,[20] và sau đó với các trung tâm chế tạo kính quang học ở Hà Lan và Đức.[21] Những nhà chế tạo kính mắt đã cải tiến các loại thấu kính để hiệu chỉnh hình ảnh dựa trên các kinh nghiệm thực tiễn thu được từ các quan sát về hiệu ứng của các thấu kính hơn là từ các lý thuyết quang học thô sơ ngày đó (các lý thuyết hồi đó còn chưa giải thích được kính mắt hoạt động như thế nào).[22][23] Những phát triển thực tiễn, làm chủ và thí nghiệm với các thấu kính dẫn tới phát minh trực tiếp ra kính hiển vi quang học vào khoảng 1595, và kính thiên văn phản xạ năm 1608, cả hai đều được làm ở các trung tâm sản xuất kính quang học ở Hà Lan.[24][25]
Đầu thế kỷ 17 Johannes Kepler nghiên cứu mở rộng lĩnh vực quang hình học, bao gồm thấu kính, sự phản xạ từ gương phẳng và gương cầu, nguyên lý chụp ảnh qua lỗ hổng, định luật tỷ lệ nghịch đảo bình phương của cường độ ánh sáng, và cách giải thích quang học cho các hiện tượng thiên văn như nguyệt thực và nhật thực và thị sai. Ông cũng suy luận đúng về vai trò của võng mạc như là một cơ quan ghi nhận hình ảnh, và Kepler có thể đánh giá định lượng một cách khoa học các hiệu ứng mà các nhà quang học quan sát từ hơn 300 năm là do từ các loại thấu kính khác nhau.[26] Sau khi kính thiên văn được phát minh ra, Kepler đã thiết lập cơ sở lý thuyết miêu tả sự hoạt động của chúng và cách để nâng cao khả năng phóng đại của kính thiên văn, mà ngày nay gọi là kính thiên văn Kepler, với hai thấu kính lồi tạo ra sự phóng đại ảnh lớn hơn so với kính thiên văn trước đó.[27]

Lý thuyết về quang học tiến triển trong giữa thế kỷ 17 với công trình của nhà bác học René Descartes, ông giải thích nhiều hiện tượng quang học khác nhau như phản xạ và khúc xạ bằng giả sử ánh sáng được phát ra từ vật tạo ra nó.[28] Điều này khác cơ bản so với quan điểm lý thuyết phát xạ của người Hy Lạp cổ đại. Cuối thập kỷ 1660 và 1670, Newton đã mở rộng ý tưởng của Descartes thành lý thuyết hạt ánh sáng, và ông nổi tiếng với công trình xác định được ánh sáng trắng là tập hợp của các tia sáng đơn sắc mà có thể tách được nhờ một lăng kính. Năm 1690, Christiaan Huygens nêu ra lý thuyết sóng ánh sáng dựa trên đề xuất do Robert Hooke nêu ra vào năm 1664. Chính Hooke đã phê bình lý thuyết của Newton về hạt ánh sáng và sự phản đối giữa hai người kéo dài cho tới tận khi Hooke qua đời. Năm 1704, Newton xuất bản cuốn Opticks và ở thời điểm đó nó đã khá thành công cũng một phần nhờ sự nổi tiếng của Newton trong lĩnh vực vật lý học. Cuộc tranh luận giữa hai người về bản chất của ánh sáng dường như có phần thắng thuộc về Newton thời đó.[28]
Quang học Newton được chấp nhận rộng rãi cho tới đầu thế kỷ 19 khi Thomas Young và Augustin-Jean Fresnel thực hiện các thí nghiệm chứng tỏ sự giao thoa của ánh sáng cho thấy bản chất sóng của ánh sáng. Thí nghiệm nổi tiếng của Young chỉ ra ánh sáng tuân theo nguyên lý chồng chập, một tính chất của các dạng sóng mà lý thuyết hạt ánh sáng của Newton không giải thích được. Thí nghiệm này dẫn tới sự ra đời của kỹ thuật nhiễu xạ ánh sáng và mở ra một lĩnh vực mới trong quang học vật lý.[29] Quang học sóng đã được thống nhất thành công với lý thuyết điện từ bởi James Clerk Maxwell trong thập kỷ 1860.[30]
Dấu mốc phát triển tiếp theo của quang học là vào năm 1899 khi Max Planck miêu tả đúng mô hình bức xạ vật đen khi giả sử sự trao đổi năng lượng giữa ánh sáng và vật chất chỉ xảy ra dưới những gói rời rạc mà ông gọi là quanta - lượng tử].[31] Năm 1905 Albert Einstein công bố lý thuyết giải thích hiệu ứng quang điện củng cố thêm cho tính chất lượng tử của ánh sáng.[32][33] Năm 1913 Niels Bohr chỉ ra rằng các nguyên tử chỉ có thể phát ra lượng năng lượng rời rạc, do vậy ông giải thích được những vạch rời rạc trong quang phổ phát xạ và quang phổ hấp thụ.[34] Hiểu biết về tương tác giữa ánh sáng và vật chất đi theo sự phát triển mới này không những là cơ sở cho ngành quang học lượng tử mà còn có vai trò quan trọng trong sự phát triển của cơ học lượng tử. Lý thuyết điện động lực học lượng tử giải thích mọi hiện tượng và quá trình quang học nói chung là kết quả của sự trao đổi các photon ảo và photon thực.[35]
Quang học lượng tử có được ứng dụng thực tiễn quan trọng kể từ khi phát minh ra maser vào năm 1953 và laser vào năm 1960.[36] Phát triển từ công trình của Paul Dirac về lý thuyết trường lượng tử, George Sudarshan, Roy J. Glauber, và Leonard Mandel đã áp dụng lý thuyết lượng tử cho trường điện từ vào các thập niên 1950 và 1960 và thu được sự hiểu biết sâu sắc hơn về sự tách sóng quang và đặc tính thống kê của ánh sáng.
Quang hình học[sửa | sửa mã nguồn]
Quang hình học có thể chia thành hai nhánh chính: quang hình học và quang học vật lý. Trong quang hình học hay quang học tia sáng, ánh sáng được coi là truyền đi theo đường thẳng, còn trong quang học vật lý hay quang học sóng, ánh sáng được coi là một dạng sóng điện từ.
Quang hình học có thể xem như là một bộ phận của quang học vật lý khi coi bước sóng ánh sáng nhỏ hơn nhiều so với các dụng cụ quang học hoặc đối với các mô hình được áp dụng.
Quang hình học[sửa | sửa mã nguồn]

Quang hình học, hay quang học tia, miêu tả sự lan truyền của ánh sáng theo định nghĩa của các "tia" đi theo đường thẳng tuân theo các định luật phản xạ và khúc xạ của tia sáng tại chỗ tiếp giáp giữa các môi trường khác nhau.[37] Những định luật này đã được phát hiện bằng thực nghiệm từ năm 984[10] và được ứng dụng để thiết kế các thành phần và dụng cụ quang học từ đó cho tới tận ngày nay. Các định luật này có thể tóm tắt như sau:
Khi một tia sáng chạm tới biên giới giữa hai môi trường trong suốt, nó chia thành tia phản xạ và khúc xạ.
- Định luật phản xạ phát biểu rằng tia phản xạ nằm trong mặt phẳng của tia tới, và góc phản xạ bằng góc tới.
- Định luật khúc xạ phát biểu rằng tia khúc xạ nằm trong mặt phẳng của tia tới, và sine của góc khúc xạ chia cho sine của góc tới là hằng số.
với n là hằng số tương ứng cho hai môi trường vật liệu và đối với từng loại bước sóng ánh sáng. Nó còn được biết đến là chiết suất (chỉ số khúc xạ).
Định luật phản xạ và khúc xạ có thể rút ra từ nguyên lý Fermat: đường đi giữa hai điểm của tia sáng là đường mà ánh sáng có thời gian ít nhất để truyền giữa hai điểm.[38]
Các xấp xỉ[sửa | sửa mã nguồn]
Quang hình học thường được đơn giản hóa bằng cách xấp xỉ bàng trục, hay "xấp xỉ góc nhỏ". Các phương trình toán học miêu tả xấp xỉ sẽ trở lên tuyến tính, cho phép các thành phần và hệ quang học được miêu tả theo các ma trận đơn giản. Phương pháp này được miêu tả bởi lý thuyết quang học Gauss và tia bàng trục, cho phép tìm ra các tính chất cơ bản của quang hệ, như hình ảnh, vị trí xấp xỉ và độ phóng đại của vật.[39]
Phản xạ[sửa | sửa mã nguồn]

Phản xạ có thể chia thành hai loại: phản xạ gương và phản xạ khuếch tán. Phản xạ gương miêu tả tính bóng của bề mặt như gương, mà phản xạ tia sáng theo cách đơn giản và tiên đoán được. Điều này cho phép tạo ra ảnh phản xạ thực (ảnh thực) hoặc ngoại suy vị trí của vật (ảnh ảo). Phản xạ khuếch tán miêu tả vật liệu có tính chất mờ đục, không trong suốt như tờ giấy hoặc đá. Sự phản xạ từ những bề mặt chỉ có thể miêu tả một cách thống kê, với sự phân bố chính xác của các tia sáng phản xạ phụ thuộc vào cấu trúc vi mô của vật liệu. Nhiều vật phản xạ khuếch tán có thể miêu tả xấp xỉ theo định luật cosine Lambert, định luật miêu tả các bề mặt có độ chói như nhau khi nhìn dưới một góc bất kỳ. Bề mặt bóng có thể quan sát thấy cả hiện tượng phản xạ gương và phản xạ khuếch tán.
Trong phản xạ gương, hướng của tia phản xạ xác định từ góc của tia tới hợp với tia pháp tuyến, tia vuông góc với mặt phẳng tại điểm tia tới chạm vào mặt phẳng. Các tia tới, tia phản xạ và tia pháp tuyến nằm trong cùng một mặt phẳng, và góc giữa tia tới và tia pháp tuyến bằng góc giữa tia phản xạ và tia pháp tuyến.[40] Đây chính là định luật phản xạ.
Đối với gương phẳng, định luật phản xạ cho biết ảnh của vật là cùng chiều và có cùng khoảng cách từ phía sau tới gương khi vật đặt trước gương. Kích thước ảnh bằng kích thước của vật. Định luật cũng cho thấy ảnh qua gương có tính đảo ngược chẵn lẻ, mà chúng ta cảm nhận như là sự đảo ngược trái phải. Ảnh tạo thành hai (hay từ số chẵn gương) gương không có tính đảo ngược chẵn lẻ. Ánh sáng phản xạ ngược từ các vật phản xạ góc tạo ra các tia phản xạ quay ngược trở lại hướng mà tia tới đến[40].
Gương có bề mặt cong có thể được mô hình bằng cách dựng tia và sử dụng định luật phản xạ tại mỗi điểm của bề mặt. Đối với gương phản xạ parabolic, các tia tới song song tạo thành các tia phản xạ hội tụ tại một điểm gọi là tiêu điểm. Những gương cong khác cũng có thể tập trung ánh sáng được, nhưng với quang sai làm biến đổi hình dạng là cho tiêu điểm của gương bị nhòe ra. Đặc biệt, các gương cầu thể hiện tính chất cầu sai. Các gương cong có thể tạo ảnh với độ phóng đại lớn hơn hoặc nhỏ hơn một đơn vị, và độ phóng đại có thể là âm, nghĩa là ảnh bị đảo ngược hướng. Ảnh cùng chiều tạo thành từ sự phản xạ qua gương luôn luôn là ảnh ảo, trong khi ảnh bị đảo ngược là ảnh thật và có thể chiếu lên màn hình.[40]
Khúc xạ[sửa | sửa mã nguồn]

Hiện tượng khúc xạ xảy ra khi ánh sáng truyền qua môi trường có chiếu suất thay đổi; đây cũng là nguyên lý cho thấu kính và sự tập trung ánh sáng. Trường hợp đơn giản nhất của khúc xạ khi tia sáng truyền qua hai môi trường đồng đều tiếp giáp nhau có chiết suất lần lượt và . Định luật Snell miêu tả góc tia khúc xạ liên hệ với góc tia tới và chiếu suất của môi trường:
với và lần lượt là góc giữa tia pháp tuyến với tia tới và giữa tia pháp tuyến với tia khúc xạ. Hiệu ứng này cũng liên quan tới sự thay đổi của tốc độ ánh sáng trong môi trường khi xét đến định nghĩa của chiết suất, và phương trình trên tương ứng với:
với và là vận tốc sóng ánh sáng tương ứng trong hai môi trường.[40]
Nhiều hệ quả của định luật Snell xuất phát từ quá trình tia sáng đi từ vật liệu có chiếu suất cao hơn vào vật liệu có chiết suất thấp hơn, do vậy có thể xảy ra trường hợp tương tác giữa ánh sáng với bề mặt cho kết quả góc khúc xạ bằng 0. Hiệu ứng này được gọi là phản xạ toàn phần và là nguyên lý cơ bản của công nghệ sợi quang học. Khi ánh sáng đi vào một sợi quang học, hiệu ứng phản xạ toàn phần cho phép ánh sáng không bị tổn hao nhiều trong suốt quá trình nó truyền dọc theo sợi quang. Các nhà vật lý cũng có thể tạo ra được ánh sáng phân cực nhờ kết hợp hai hiệu ứng phản xạ và khúc xạ: Khi tia khúc xạ hợp với tia phản xạ một góc vuông thì lúc này tia khúc xạ có tính chất "phân cực phẳng". Góc tới thỏa mãn trường hợp này thường được gọi là góc Brewster.[40]
Định luật Snell còn dùng để tiên đoán sự lệch của tia sáng khi nó truyền qua "môi trường tuyến tính" khi đã biết chiết suất và hình học cấu trúc của môi trường. Ví dụ, ánh sáng truyền qua một lăng kính sẽ bị lệch hướng phụ thuộc vào hình dáng và chiết suất của lăng kính. Thêm vào đó, do các tần số ánh sáng khác nhau có chiết suất khác nhau đối với cùng một môi trường vật liệu, hiện tượng khúc xạ có thể được sử dụng để tạo ra phổ tán sắc giống như đối với cầu vồng. Isaac Newton là người đầu tiên phát hiện ra hiệu ứng này khi ông cho ánh sáng Mặt Trời truyền qua một lăng kính đặt trong phòng tối.[40]
Một số môi trường có chiết suất thay đổi dần theo vị trí trong nó, và do vậy ánh sáng truyền qua nó bị cong đi. Hiệu ứng này là nguyên nhân tạo ra ảo ảnh khi nhìn trên mặt đường bê tông nhựa vào những ngày nắng nóng khi chiết suất của các lớp không khí thay đổi làm cho tia sáng bị bẻ cong, tạo ra sự phản xạ khi nhìn từ xa. Vật liệu có chỉ số khúc xạ biến đổi được gọi là vật liệu có gradien chiết suất (GRIN) và nó có nhiều tính chất quan trọng áp dụng trong công nghệ quét quang học như ở máy photocopy và máy scan. Lĩnh vực nghiên cứu tính chất này gọi là quang học gradien chiết suất.[41]

Một vật dùng để hội tụ hay phân kỳ các tia sáng gọi là thấu kính. Các thấu kính mỏng tạo ra hai tiêu điểm có thể được miêu tả nhờ phương trình thấu kính.[42] Nói chung có hai loại thấu kính: thấu kính lồi có thể hội tụ các tia sáng song song, và thấu kính lõm làm cho các tia sáng song song phân kỳ. Việc miêu tả sự tạo ảnh có thể thu được nhờ phương pháp dựng tia (vẽ ảnh) tương tự như đối với các gương cong. Các thấu kính mỏng có thể được tính toán đơn giản tuân theo phương trình sau xác định lên vị trí của ảnh khi biết tiêu cự () của thấu kính và khoảng cách tới vật ():
với là khoảng cách tới ảnh và được quy ước có giá trị âm khi ảnh nằm cùng phía với vật và có giá trị dương khi ảnh nằm ở phía bên kia vật so với thấu kính.[42] Đối với thấu kính lõm quy ước tiêu cự f có giá trị âm.

Các tia tới song song hội tụ qua thấu kính lồi (thấu kính hội tụ) tạo ảnh thật ngược chiều nằm tại tiêu điểm ở phía bên kia của thấu kính. Các tia từ một vật ở khoảng cách gần hội tụ tại điểm có khoảng cách đến thấu kính lớn hơn tiêu cự; vật càng gần thấu kính thì ảnh tạo thành nằm càng xa thấu kính. Đối với thấu kính lõm, các tia tới song song phân kỳ sau khi đi qua thấu kính theo cách nếu kéo dài các tia ló thì chúng sẽ cắt nhau tại tiêu điểm của thấu kính lõm và nằm cùng phía với các tia tới, hay thấu kính lõm tạo ảnh ảo. Các tia từ vật ở khoảng cách gần cho ảnh ảo nằm gần thấu kính hơn so với tiêu cự và nằm cùng phía với vật. Vật càng nằm gần thấu kính, ảnh ảo càng nằm gần thấu kính.
Độ phóng đại của thấu kính được định nghĩa là:
với quy ước dấu âm để cho khi tạo ảnh ảo thì M có giá trị dương và ảnh thật thì M có giá âm. Tương tự như gương phẳng, ảnh cùng chiều với vật là ảnh ảo trong khi ảnh ngược chiều với vật là ảnh thật.[40]
Thấu kính cũng chịu hiện tượng quang sai làm mờ hay nhòe ảnh và tiêu điểm. Nguyên nhân của hiện tượng này là do sự không hoàn hảo về cấu trúc hình học của thấu kính và do sự thay đổi chiết suất đối với các bước sóng ánh sáng khác nhau (sắc sai).[40]

Quang học vật lý[sửa | sửa mã nguồn]
Trong quang học vật lý (hay quang học sóng), tính chất sóng của ánh sáng được nghiên cứu đến. Tính chất này cho phép giải thích được các hiện tượng như giao thoa và nhiễu xạ mà quang hình học không thể giải thích được. Tốc độ sóng ánh sáng trong không khí xấp xỉ 3,0×108 m/s (chính xác bằng 299.792.458 m/s trong chân không). Bước sóng của ánh sáng khả kiến thay đổi trong khoảng 400 và 700 nm, nhưng thuật ngữ "ánh sáng" cũng được áp dụng cho miền bức xạ hồng ngoại (0,7–300 μm) và tử ngoại (10–400 nm).
Mô hình sóng có thể dùng để thực hiện các tiên đoán một hệ quang học hành xử ra sao mà không cần đòi hỏi phải giải thích "sóng" là cái gì trong môi trường đó. Cho đến tận giữa thế kỷ 19, hầu hết các nhà vật lý tin rằng môi trường "ether" cho phép ánh sáng lan truyền trong nó.[43] Cho tới năm 1865 sự tồn tại của sóng điện từ mới được biết đến thông qua phương trình Maxwell. Sóng điện từ truyền đi với tốc độ ánh sáng và có điện trường và từ trường biến đổi và vuông góc với nhau, cũng như chúng vuông góc với hướng lan truyền của sóng.[44] Sóng ánh sáng là một loại sóng điện từ và khi nghiên cứu ở cấp độ nguyên tử các tính chất lượng tử của nó mới được thể hiện.
Mô hình và thiết kế hệ thống quang học sử dụng quang học sóng[sửa | sửa mã nguồn]
Có nhiều cách xấp xỉ đơn giản cho thiết kế và phân tích các quang hệ. Đa số sử dụng một đại lượng vô hướng để biểu diễn trường điện từ của sóng ánh sáng, hơn là sử dụng vectơ với các vectơ điện và vectơ từ vuông góc với nhau.[45] Phương trình Huygens–Fresnel là một trong những mô hình như thế. Mô hình này do Fresnel rút ra từ thực nghiệm vào năm 1815, dựa trên giả thuyết của Huygen rằng mỗi điểm nằm trên đầu sóng là nguồn cho các sóng thứ cấp mới; và sự lan truyền của toàn bộ là tổng của các sóng thứ cấp đến từ mọi điểm trong môi trường mà sóng đã đi qua, mà Fresnel kết hợp với nguyên lý giao thoa của sóng. Phương trình Huygens-Fresnel có nền tảng vật lý từ phương trình nhiễu xạ Kirchhoff, mà nó thu được từ phương trình Maxwell. Ví dụ về ứng dụng của nguyên lý Huygens–Fresnel như giải thích các hiện tượng khúc xạ và mô hình khúc xạ Fraunhofer.
Những mô hình phức tạp hơn, bao hàm mô hình về điện trường và từ trường của sóng ánh sáng, đòi hỏi cần thiết khi xét tới tương tác giữa ánh sáng và vật chất nơi tương tác này phụ thuộc vào tính chất điện và tính chất từ của vật chất. Ví dụ, hành xử của ánh sáng tương tác với bề mặt kim loại rất khác với khi nó tương tác với vật liệu điện môi. Mô hình vectơ cũng cần thiết khi giải thích sự phân cực của ánh sáng.
Các kỹ thuật mô phỏng bằng máy tính như sử dụng phương pháp phần tử hữu hạn, phương pháp phần tử biên có thể dùng để mô hình hóa sự lan truyền của ánh sáng trong hệ mà không thể thu được nghiệm giải tích. Những mô hình này đòi hỏi phương pháp số và thường dùng để giải các vấn đề yêu cầu độ chính xác tương đối xấp xỉ so với các nghiệm giải tích thu được.[46]
Tất cả các kết quả của quang hình học có thể rút ra nhờ kỹ thuật của lĩnh vực quang học Fourier mà có thể áp dụng cho nhiều kỹ thuật toán học và phân tích sử dụng trong kỹ thuật âm thanh và xử tín hiệu.
Phương pháp hàm Gauss về sự lan truyền của chùm điện từ là mô hình quang học vật lý bàng trục cho sự lan truyền của bức xạ kết hợp như chùm laser. Kỹ thuật này có tính đến hiện tượng khúc xạ, cho phép tính toán chính xác tỷ lệ một chùm laser mở rộng theo khoảng cách, và kích thước tối thiểu mà chùm có thể tập trung được. Phương pháp hàm Gauss đã bắc cầu nối khoảng cách giữa quang hình học và quang học vật lý.[47]
Chồng chập và giao thoa[sửa | sửa mã nguồn]
Khi không có hiệu ứng phi tuyến, nguyên lý chồng chập được sử dụng để tiên đoán hình dạng của sóng thông qua cách cộng sóng.[48] Tương tác giữa các sóng tạo ra các phần "giao thoa", như giao thoa tăng cường hoặc giao thoa triệt tiêu. Nếu hai sóng có cùng bước sóng và tần số trong trạng thái cùng pha, cả đỉnh sóng và bụng sóng của mỗi sóng sẽ khớp với nhau. Kết quả này dẫn tới giao thoa tăng cường làm tăng biên độ của sóng, mà đối với ánh sáng sẽ là sự sáng lên của cường độ tại vị trí đó. Mặt khác, nếu hai sóng có cùng bước sóng và tần số những ngược pha nhau, thì đỉnh sóng của sóng này khớp với bụng sóng của sóng kia và ngược lại. Kết quả là giao thoa triệt tiêu và giảm biên độ sóng, mà đối với ánh sáng sẽ là sự mờ đi của cường độ tại vị trí đó. Hình vẽ dưới minh họa hiệu ứng này.[48]
| Sóng tổng hợp |

| |
| sóng 1 | ||
| Sóng 2 | ||
| Hai sóng cùng pha | Hai sóng ngược pha 180° | |

Nguyên lý Huygens–Fresnel phát biểu rằng mỗi điểm nằm trên đầu sóng là nguồn cho sóng thứ cấp mới, do vậy các đầu sóng có thể tạo ra các phần giao thoa tăng cường hoặc triệt tiêu ở những vị trí khác nhau tạo ra những miền sáng và tối đồng đều và tiên đoán được.[48] Giao thoa là một ngành khoa học đo đạc những mẫu hình này, thường là để xác định chính xác khoảng cách và độ phân giải góc.[49] Giao thoa kế Michelson là một dụng cụ nổi tiếng nhằm sử dụng hiệu ứng giao thoa để đo một cách chính xác sự phụ thuộc của tốc độ ánh sáng theo hướng lan truyền trong chân không.[50]
Tính chất của các màng mỏng ảnh hưởng trực tiếp tới hiệu ứng giao thoa. Các lớp phủ chống phản xạ dùng để triệt tiêu giao thoa làm giảm tính phản xạ của bề mặt được phủ lớp đó, do vậy giảm thiểu độ lóa và những phản xạ không mong muốn. Trường hợp gioa thoa đơn giản nhất là một lớp mỏng với độ dày bằng một phần tư bước sóng của ánh sáng tới. Sóng ánh sáng phản xạ từ đỉnh của màng và sóng ánh sáng phản xạ từ đáy màng lúc này lệch pha nhau 180°, làm cho giao thoa triệt tiêu. Các sóng chỉ lệch pha nhau đối với từng bước sóng một, mà người ta có thể chọn sóng ở giữa miền phổ khả kiến, trong bước sóng khoảng 550 nm. Các thiết kế phức tạp hơn sử dụng nhiều màng mỏng có thể đạt được triệt tiêu độ phản xạ trên phổ rộng hơn, hoặc độ phản xạ cực thấp cho riêng một bước sóng.
Tính chất giao thoa tăng cường ở các màng mỏng dùng để tạo ra sự phản xạ mạnh ánh sáng ở nhiều bước sóng, mà cũng phụ thuộc vào thiết kế và độ dày của màng. Các lớp này được dùng để tạo ra gương điện môi, màng lọc giao thoa, máy phản xạ nhiệt, và màng lọc màu trong các camera truyền hình màu. Hiệu ứng giao thoa cũng là nguyên nhân của hình ảnh bảy sắc cầu vồng nhìn thấy ở lớp dầu tràn.[48]
Nhiễu xạ[sửa | sửa mã nguồn]

Nhiễu xạ là quá trình ánh sáng giao thoa khi nó gặp phải vật cản hoặc đi qua hai khe. Francesco Maria Grimaldi là người đầu tiên đã quan sát thấy hiệu ứng này vào năm 1665, và ông gọi nó bằng tiếng Latin là diffringere, 'bị phân thành từng mảnh'.[51][52] Cuối thế kỷ này, Robert Hooke và Isaac Newton cũng miêu tả hiện tượng mà ngày nay được biết đến là vành Newton khi quan sát nó qua một thấu kính lồi đặt trên mặt phẳng,[53] trong khi đó nhà thiên văn James Gregory cũng quan sát thấy các vân giao thoa từ lông vũ.[54]
Mô hình quang học vật lý đầu tiên về nhiễu xạ dựa trên nguyên lý Huygens–Fresnel được Thomas Young phát triển vào năm 1803 bằng thí nghiệm giao thoa của ông khi cho ánh sáng đi qua hai khe hẹp nằm gần nhau. Young nhận thấy kết quả ông thu được chỉ có thể giải thích khi hai khe được coi như là hai nguồn sóng chứ không đơn thuần là những khe hở.[55] Năm 1815 và 1818, Augustin-Jean Fresnel thiết lập lên cơ sở toán học của hiện tượng nhiễu xạ đối với các vân giao thoa qua hai khe.[42]
Mô hình đơn giản nhất miêu tả nhiễu xạ sử dụng các phương trình cho độ phân giải góc của các vân sáng và vân tối đối với bước sóng λ. Nói chung, phương trình có dạng
với là khoảng cách giữa hai nguồn đầu sóng (trong trường hợp thí nghiệm Young, nó là khoảng cách giữa hai khe), là độ phân giải góc (hoặc khoảng cách góc) giữa vân trung tâm và vân thứ , với vân trung tâm khi .[56]
Phương trình này chỉ bị sửa đổi một chút khi xét trường hợp nhiễu xạ qua một khe, hoặc qua nhiều khe, hay đối với cách tử nhiễu xạ chứa rất nhiều khe nằm cách đều nhau.[56] Những mô hình phức tạp hơn về hiệu ứng nhiễu xạ đòi hỏi các mô hình toán học như nhiễu xạ Fresnel hoặc nhiễu xạ Fraunhofer.[57]
Nhiễu xạ tia X dựa trên nguyên lý rằng có thể dùng các nguyên tử với khoảng cách rất đều nhau trong dàn tinh thể cỡ vài angstrom để làm cách tử. Để nhìn thấy các phần nhiễu xạ, tia X với bước sóng gần bằng khoảng cách giữa hai nguyên tử gần nhau được chiếu vào tinh thể. Vì tinh thể là cách tử nhiễu xạ có cấu trúc ba chiều, các vân nhiễu xạ biến đổi phụ thuộc vào hai hướng theo như định luật Bragg, và những vân này có đặc trưng duy nhất đối với từng tinh thể và khoảng cách giữa hai nguyên tử.[56]
Hiệu ứng nhiễu xạ giới hạn khả năng phát hiện sự tách biệt của nguồn sáng đối với máy dò quang học. Nói chung, ánh sáng đi qua lỗ của máy dò sẽ chịu ảnh hưởng của hiệu ứng nhiễu xạ và ảnh tốt nhất thu được (giới hạn nhiễu xạ quang học) nằm tại điểm trung tâm xung quanh vành sáng, tách biệt với các mảng tối; những hình này còn được biết tới là vân Airy, cùng với điểm sáng trung tâm của nó gọi là đĩa Airy.[42] Độ lớn của đĩa được cho bởi
với θ là độ phân giải góc, λ là bước sóng của ánh sáng, và D là đường kính của lỗ hổng (độ mở) thấu kính. Nếu độ phân giải góc giữa hai điểm nhỏ hơn nhiều bán kính góc của đĩa Airy, thì không thể phân biệt được hai điểm trong bức ảnh, nhưng nếu ngược lại thì sẽ thấy ảnh rõ ràng của hai điểm. Rayleigh định nghĩa "tiêu chuẩn giới hạn Rayleigh" rằng hai điểm có khoảng cách góc bằng bán kính của đĩa Airy (đo tới vân tối đầu tiên) có thể coi như là được phân giải. Các thấu kính có đường kính lớn hơn hoặc độ mở lớn hơn sẽ cho độ phân giải cao hơn.[56] Các giao thoa kế thiên văn với khả năng tạo ra độ mở rất lớn, cho phép thu được độ phân giải góc lớn nhất có thể.[49]
Đối với kỹ thuật chụp ảnh thiên văn, khí quyển ngăn cản độ phân giải tối ưu đạt được trong phổ khả kiến do khí quyển làm tán xạ và phân tán ánh sáng từ các ngôi sao khiến khi quan sát chúng thấy hình ảnh của sao như đang nhấp nháy. Các nhà thiên văn học coi hiệu ứng này để đánh giá chất lượng điều kiện quan sát thiên văn. Các kỹ thuật mới như quang học thích nghi đã được phát minh nhằm loại bỏ ảnh hưởng của tầng khí quyển đến chụp ảnh thiên văn và đã đạt tới giới hạn nhiễu xạ.[58]
Hiện tượng tán sắc và tán xạ[sửa | sửa mã nguồn]

Quá trình khúc xạ diễn ra trong giới hạn quang học vật lý, và khi bước sóng ánh sáng có độ lớn gần bằng khoảng cách đang xét đến thì lúc này xảy ra hiện tượng tán xạ. Loại tán xạ đơn giản nhất là tán xạ Thomson xảy ra khi sóng điện từ bị lệch bởi một hạt. Trong giới hạn tán xạ Thompson, khi bản chất sóng của hạt lấn át, ánh sáng bị tán sắc độc lập với tần số sóng, điều này ngược hẳn với tán xạ Compton khi nó phụ thuộc tần số và có tính chất chi phối bởi cơ học lượng tử, khi ánh sáng thể hiện bản chất hạt rõ hơn. Theo ý nghĩa thống kê, tán xạ đàn hồi của ánh sáng bởi một số lớn hạt có kích cỡ nhỏ hơn bước sóng ánh sáng được biết tới như là quá trình tán xạ Rayleigh trong khi quá trình tương tự đối với tán xạ bởi hạt có kích cỡ tương đương hoặc lớn hơn bước sóng ánh sáng được biết tới là tán xạ Mie với hiệu ứng Tyndall là kết quả được quan sát phổ biến. Một phần nhỏ ánh sáng tán xạ từ nguyên tử hoặc phân tử có thể trải qua tán xạ Raman, khi sự thay đổi tần số là do trạng thái kích thích của nguyên tử hoặc phân tử. Tán xạ Brillouin xảy ra khi tần số ánh sáng thay đổi do vị trí thay đổi theo thời gian và sự chuyển động của vật liệu tỉ trọng lớn.[59]
Sự tán sắc xảy ra khi các tần số ánh sáng khác nhau có vận tốc pha khác nhau, hoặc là do tính chất của vật liệu (tán sắc do vật liệu) hoặc do hình học của ống dẫn sóng quang học (tán sắc do ống dẫn sóng). Hiện tượng tán sắc hay gặp nhất là khi có sự giảm chiết suất cùng với tăng bước sóng, mà có thể quan sát thấy ở đa số vật liệu trong suốt. Hiện tượng này được gọi là "tán sắc thông thường". Nó xảy ra trong mọi chất điện môi, khi bước sóng nằm trong miền mà chất điện môi không hấp thụ ánh sáng.[60] Trong miền bước sóng mà môi trường hấp thụ đáng kể, chiết suất có thể tăng theo bước sóng. Hiện tượng này gọi là "tán sắc dị thường".[40][60]
Quang phổ màu sắc thu được thông qua lăng kính là một ví dụ của hiện tượng tán sắc thông thường. Tại bề mặt lăng kính, định luật Snell tiên đoán rằng ánh sáng tới một góc bằng θ so với pháp tuyến sẽ bị khúc xạ một góc arcsin(sin (θ) / n). Do vậy, ánh sáng lam, với chỉ số khúc xạ cao hơn, bị lệch mạnh hơn so với ánh sáng đỏ, với kết quả là hình thành lên các thành phần màu của bảy sắc cầu vồng.[40]

Vật liệu tán sắc thường được đặc trưng bởi số Abbe, cho phép định lượng một cách đơn giản sự tán sắc trên cơ sở chỉ số khúc xạ ở ba bước sóng khác nhau. Sự tán sắc do ống dẫn sóng phụ thuộc vào hằng số lan truyền.[42] Cả hai loại tán sắc làm sự thay đổi đặc trưng nhóm của sóng, đặc điểm mà gói sóng thay đổi với cùng tần số như của biên độ sóng. "Tán sắc do vận tốc nhóm" biểu hiện như là sự lan tỏa của "đường bao" tín hiệu của bức xạ và xác định bằng tham số độ trễ tán sắc nhóm:
với là vận tốc nhóm.[61] Đối với môi trường đồng nhất, vận tốc nhóm là
với n là chỉ số khúc xạ (chiết suất), c là tốc độ ánh sáng trong chân không.[62] Từ đây thu được công thức đơn giản hơn cho tham số độ trễ tán sắc:
Nếu D nhỏ hơn 0, người ta nói môi trường có tính tán sắc dương hoặc tán sắc thông thường. Nếu D lớn hơn 0, môi trường có tính tán sắc âm. Nếu một xung ánh sáng lan truyền qua môi trường tán sắc thông thường, khi đó thành phần có tần số cao hơn sẽ lan truyền chậm hơn thành phần có tần số thấp hơn. Khi đó xung trở thành xung có tần số tăng dần, tức là tần số tăng theo thời gian. Điều này có nghĩa là phổ thoát ra khỏi lăng kính cho thấy ánh sáng đỏ bị khúc xạ ít nhất và ánh sáng lam và cực tím bị khúc xạ nhiều nhất. Ngược lại, nếu một xung lan truyền qua môi trường có tính sắc dị thường (tán sắc âm), các thành phần có tần số cao hơn sẽ di chuyển nhanh hơn thành phần có tần số thấp hơn, và xung trở thành xung có tần số giảm dần, hay tần số giảm dần theo thời gian.[63]
Kết quả của hiện tượng tán sắc vận tốc nhóm, dù là tán sắc dương hay âm, ảnh hưởng quan trọng tới thời gian trải ra của xung tín hiệu. Điều này khiến cho kỹ thuật xử lý sự tán sắc là cực kỳ quan trọng trong hệ thống viễn thông quang học dựa trên sợi quang học, do nếu sự tán sắc quá lớn thì nhóm xung biểu thị thông tin sẽ trải ra theo thời gian và trộn lẫn nhau, khiến cho rất khó có thể chiết tách được thông tin.[61]
Phân cực[sửa | sửa mã nguồn]
Sự phân cực là tính chất chung của sóng miêu tả hướng dao động của chúng. Đối với sóng ngang như ở đa số sóng điện từ, nó miêu tả hướng dao động trong mặt mặt phẳng vuông góc với phương truyền sóng. Sự dao động có thể chỉ theo một hướng (phân cực thẳng hay phân cực tuyến tính), hoặc hướng dao động có thể quay khi sóng truyền đi (phân cực tròn hoặc phân cực ellip). Sóng phân cực tròn có thể quay sang phải hoặc sang trái theo hướng truyền sóng, và mỗi hướng quay này trong sóng được gọi là tính chất chiral của sóng.[64]
Cách điển hình để xem xét tính phân cực đó là tìm ra hướng của vectơ điện trường khi sóng điện từ lan truyền. Vectơ điện trường của sóng phẳng có thể phân tích thành hai vectơ thành phần bất kỳ vuông góc với nhau ký hiệu là x và y (với z là trục của phương truyền sóng). Hình dạng chiếu trên mặt phẳng x-y của vectơ điện trường là đường cong Lissajous miêu tả trạng thái phân cực.[42] Những hình sau minh họa một vài ví dụ về hướng của vectơ điện trường (lam), ở thời điểm t (trục đứng), tại một điểm bất kỳ trong không gian, với các thành phần x và y (đỏ/trái và lam/phải), và hình chiếu quỹ đạo quét của vectơ trên mặt phẳng: cùng xảy ra một chu kỳ khi nhìn vào điện trường ở một thời điểm nhất định khi dịch chuyển điểm trong không gian, dọc theo hướng ngược lại với hướng lan truyền.
Trong hình ngoài cùng bên trái, các thành phần x và y của sóng ánh sáng đồng pha với nhau. Trong trường hợp này, tỉ số của biên độ của chúng là hằng số, do vậy hướng của vectơ điện trường (vectơ tổng của hai vectơ thành phần) là không đổi. Do đó hình chiếu của nó lên mặt phẳng vuông góc với phương truyền sóng tạo thành một đoạn thẳng, hay trường hợp này chính là sự phân cực tuyến tính. Hướng của đoạn thẳng phụ thuộc vào độ lớn (biên độ) của hai vec tơ thành phần.[64]
Trong hình ở giữa, hai thành phần x và y vuông góc với nhau có cùng biên độ và lệch pha nhau 90°. Trong trường hợp này, một thành phần có giá trị bằng 0 khi thành phần kia có biên độ cực đại hoặc cực tiểu. Có hai khả năng để thỏa mãn điều kiện này: thành phần x có thể sớm pha 90° so với thành phần y hoặc có thể chậm pha 90° so với thành phần y. Trong trường hợp đặc biệt này, vectơ điện trường quét lên một đường tròn trong mặt phẳng, nên sự phân cực này gọi là sự phân cực tròn. Hướng quay của vectơ điện trường phụ thuộc vào mối liên hệ pha giữa hai thành phần và tương ứng với phân cực tròn bên phải và phân cực tròn bên trái.[42]
Trong trường hợp tổng quát, khi hai thành phần không có cùng biên độ và hoặc sự lệch pha của chúng không bằng 0 hay số nguyên lần của 90°, sự phân cực được gọi là phân cực elip bởi vì vectơ điện trường vạch lên một đường elip trong mặt phẳng (phân cực elip). Trường hợp này minh họa ở hình ngoài cùng bên phải. Mô tả toán học chi tiết của sự phân cực này sử dụng phép tính Jones và được đặc trưng bởi tham số Stokes.[42]
Thay đổi sự phân cực[sửa | sửa mã nguồn]
Các môi trường có chiết suất khác nhau tương ứng với các loại phân cực khác nhau được gọi là lưỡng chiết.[64] Những biểu hiện thường gặp ở hiệu ứng này là chất làm trễ pha (wave plates/retarders) trong phân cực thẳng và hiệu ứng Faraday/sự quay quang học trong phân cực tròn.[42] Nếu quãng đường trong môi trường lưỡng chiết là đáng kể, sóng phẳng sẽ đi ra khỏi vật liệu với hướng truyền bị thay đổi đáng kể do hiện tượng khúc xạ. Ví dụ, trong trường hợp đối với tinh thể canxit, người quan sát sẽ thấy hai ảnh phân cực vuông góc với nhau khi tia sáng đi xuyên qua chúng. Đây cũng là hiện tượng đầu tiên chứng tỏ có sự phân cực khi Erasmus Bartholinus quan sát thấy vào năm 1669. Thêm vào đó, sự dịch chuyển pha, và do đó làm thay đổi trạng thái phân cực, thường là phụ thuộc vào tần số sóng, khi đi tới vật liệu óng ánh (dichroism), sẽ tạo ra hiệu ứng nhiều mằu sắc như cầu vồng. Trong ngành khoáng vật học, những tính chất này gọi là hiện tượng đa sắc, và các nhà khoáng vật học dùng để nhận ra khoáng chất dưới kính hiển vi phân cực. Ngoài ra, nhiều chất dẻo bình thường không có tính lưỡng chiết sẽ có tính này khi chịu ứng suất cơ học, một hiện tượng trong lĩnh vực quang đàn hồi học.[64] Những phương pháp khác lưỡng chiết, để có thể quay sự phân cực thẳng của chùm sáng, bao gồm lăng trụ quay phân cực sử dụng hiệu ứng phản xạ toàn phần của lăng kính để thiết kế sự truyền ánh sáng đồng phân cực phẳng một cách hữu hiệu.[65]

Trong hình này, θ1 – θ0 = θi.
Có những vật liệu làm giảm biên độ của một số loại sóng phân cực nhất định, mà chúng gần như cản mọi bức xạ theo một loại phân cực như thiết bị lọc phân cực hay kính phân cực. Định luật Malus, đặt theo tên của Étienne-Louis Malus, nói rằng khi chiếu chùm sáng phân cực thẳng vào một thiết bị phân cực hoàn hảo, cường độ I của chùm sáng vượt qua nó được cho bởi
với
- I0 là cường độ của chùm sáng tới,
- và θi là góc giữa hướng của ánh sáng phân cực ban đầu với trục của thiết bị phân cực.[64]
Một chùm sáng không phân cực về lý thuyết có thể coi như là hỗn hợp của các tia phân cực ở mọi trạng thái. Do giá trị trung bình của là 1/2, hệ số truyền qua trở thành
Thực tế, cường độ chùm sáng bị mất một phần khi đi qua thiết bị phân cực và cường độ chùm sáng đi ra sẽ bị giảm hơn so với tính toán ở công thức trên, vào khoảng 38% đối với kính phân cực và cao hơn đáng kể (>49,9%) ở một số lăng kính lưỡng chiết.[42]
Ngoài chất lưỡng chiết và ở một số vật liệu óng ánh, hiệu ứng phân cực cũng xuất hiện ở mặt tiếp xúc giữa hai loại vật liệu có chiết suất khác nhau. Các hiệu ứng này có thể miêu tả bằng phương trình Fresnel. Một phần sóng được truyền qua và phần còn lại thì phản xạ, với tỷ lệ giữa hai phần này phụ thuộc vào góc tới và góc khúc xạ. Theo cách này, quang học vật lý trở lại với định nghĩa góc Brewster.[42] Khi ánh sáng phản xạ từ màng mỏng, sự giao thoa giữa ánh sáng phản xạ từ mảng mỏng có thể tạo ra sự phân cực.
Ánh sáng tự nhiên[sửa | sửa mã nguồn]

Hầu hết các nguồn bức xạ điện từ chứa nhiều phân tử và nguyên tử phát ra bức xạ. Hướng của điện trường tạo ra bởi các nguồn này có thể không tương quan với nhau, trong trường hợp này ánh sáng được coi là không phân cực. Nếu có sự tương quan một phần giữa các nguồn, ánh sáng sẽ phân cực một phần. Nếu toàn bộ dải phổ ánh sáng của nguồn phân cực đều như nhau, ánh sáng phân cực một phần có thể được miêu tả như là kết quả của sự chồng chập hoàn toàn của thành phần ánh sáng không phân cực với thành phần ánh sáng phân cực. Từ đây có thể mô tả ánh sáng theo số hạng "bậc phân cực", và tham số phân cực elip.[42]
Ánh sáng phản xạ twf vật liệu trong suốt bị phân cực một phần hay toàn bộ, ngoại trừ tia sáng vuông góc với bề mặt vật liệu. Hiệu ứng này cho phép nhà toán học Étienne-Louis Malus thí nghiệm và đưa ra mô hình toán học về ánh sáng phân cực. Sự phân cực xuất hiện khi ánh sáng tán xạ trong khí quyển. Ánh sáng tán xạ tạo ra độ trắng và nền màu xanh da trời khi trời quang mây. Sự phân cực một phần này của ánh sáng tán xạ đem lại thuận lợi cho khoa học chụp ảnh khi áp dụng thêm các bộ lọc phân cực để thu được chất lượng ảnh tốt hơn. Sự phân cực quang học có vai trò quan trọng trong hóa học do hiệu ứng quay quang học và phân cực tròn ("lưỡng chiết tròn") thể hiện ở các phân tử quang hóa học.[42]
Quang học hiện đại[sửa | sửa mã nguồn]
Quang học hiện đại bao hàm các lĩnh vực khoa học quang học và kỹ thuật quang học mà đã trở thành phổ biến trong thế kỷ 20. Những lĩnh vực của khoa học quang học thường liên quan tới các tính chất điện từ hoặc tính chất cơ học lượng tử của ánh sáng và cũng liên quan tới các chủ đề khác. Một nhánh chính của quang học, quang học lượng tử, nghiên cứu các tính chất cơ lượng tử của ánh sáng. Quang học lượng tử không chỉ là lý thuyết; một số thiết bị hiện đại, như laser, có nguyên lý hoạt động dựa trên cơ học lượng tử. Những thiết bị phát hiện ánh sáng, như ống nhân quang và ống nhân electron, có độ nhạy với từng photon. Các cảm biến ảnh điện tử, như CCD, có độ ồn Poisson tương ứng với mức thống kê của từng photon sự kiện. Diode phát sáng và tế bào quang điện, cũng hoạt động dựa trên những nguyên lý của cơ học lượng tử. Trong nghiên cứu những thiết bị này, các nhà khoa học thường kết hợp quang học lượng tử với lĩnh vực điện tử lượng tử.[66]
Các nghiên cứu chuyên biệt của quang học bao gồm nghiên cứu ánh sáng tương tác như thế nào với vật liệu như trong quang học tinh thể và siêu vật liệu. Những nghiên cứu khác tập trung vào các hiệu ứng của sóng điện từ trong quang học kỳ dị, quang học truyền bức xạ, quang học phi tuyến, quang học thống kê, và kỹ thuật đo lường bức xạ. Thêm vào đó, ngành kỹ thuật máy tính đã thu hút sự chú ý và phát triển của các lĩnh vực như mạch tích hợp quang học, công nghệ thị giác ở máy, và tính toán quang học, mở ra hướng đi triển vọng cho thế hệ máy tính tiếp theo.[67]
Ngày nay, khoa học quang học thuần túy được gọi là khoa học quang học hay vật lý quang học để phân biệt nó với khoa học quang học ứng dụng, mà có thể coi là kỹ thuật quang học. Những lĩnh vực con của kỹ thuật quang học bao gồm kỹ thuật chiếu sáng, quang tử học, và điện tử quang với những ứng dụng thực tiễn như thiết kế thấu kính, sản xuất và kiểm định các thành phần quang học, và kỹ thuật xử lý hình ảnh. Một số lĩnh vực này có liên hệ với nhau, mà đôi khi sự phân biệt giữa các chủ đề chỉ ở thứ hơi khác trong lĩnh vực công nghiệp trên nhiều nơi trên thế giới. Cộng đồng các nhà nghiên cứu trong quang học phi tuyến đã phát triển lớn mạnh từ nhiều thập kỷ kể từ khi phát triển công nghệ laser.[68]
Laser[sửa | sửa mã nguồn]

Máy phát tia laser là thiết bị phát ra ánh sáng thông qua cơ chế phát xạ kích thích. Thuật ngữ laser là từ viết tắt của Light Amplification by Stimulated Emission of Radiation - Khuếch đại ánh sáng bằng bức xạ kích thích.[69] Ánh sáng laser có độ định hướng cao (tính kết hợp), tức là chùm sáng phát ra hoặc có độ rộng hẹp, độ phân kỳ của chùm thấp, hoặc có thể hội tụ chúng lại nhờ các thiết bị quang học như thấu kính. Bởi vì sóng vi ba cũng có thể bị phát xạ kích thích tương tự như laser, và hiệu ứng maser đã được phát triển đầu tiên, các thiết bị phát ra bức xạ kích thích trong bước sóng vi ba và sóng vô tuyến thường gọi là maser.[70]

Công trình hiện thực hóa laser đầu tiên bởi Theodore Maiman tại Phòng thí nghiệm nghiên cứu Hughes vào ngày 16 tháng 5 năm 1960.[72] Lần đầu tiên khi được phát minh ra, người ta gọi chúng là "một giải pháp cho một vấn đề".[73] Kể từ đó, laser đã trở thành nền tảng cho công nghiệp với doanh thu hàng tỷ đô la, với hàng nghìn ứng dụng đa dạng của nó. Ứng dụng của laser có thể thấy ở đời sống thường nhật là ở máy quét mã vạch tại các siêu thị phát minh vào năm 1974.[74] Các đầu đọc đĩa laser, phát minh vào năm 1978, là một sản phẩm thương mại thành công đầu tiên có mặt laser, nhưng phải cho tới năm 1982 khi đầu đọc đĩa compact trang bị laser thì laser mới thực sự trở thành sản phẩm tiêu dùng có mặt tại từng gia đình.[75] Những ổ đĩa quang này sử dụng laser bán dẫn có độ tập trung nhỏ hơn một milimét có thể quét bề mặt đĩa để đọc dữ liệu ghi trên nó. Viễn thông sợi quang học dựa trên laser để truyền lượng lớn thông tin với tốc độ gần bằng tốc độ ánh sáng. Những ứng dụng khác của laser bao gồm máy in laser và bút laser. Trong y học các nhà khoa học sử dụng laser để phẫu thuật không chảy máu, phẫu thuật mắt lazik, và phân lập tế bào bằng laser; trong công nghiệp quốc phòng sự có mặt của laser như ở hệ thống phòng thủ tên lửa, và cảm biến từ xa lidar. Laser cũng sử dụng trong kỹ thuật chụp ảnh toàn ký, bubblegram, trình diễn ánh sáng laser...[76]
Hiệu ứng Kapitsa–Dirac[sửa | sửa mã nguồn]
Hiệu ứng Kapitsa–Dirac làm các chùm hạt bị nhiễu xạ khi gặp sóng đứng ánh sáng. Ánh sáng có thể dùng để định vị vật chất thông qua nhiều hiệu ứng khác nhau.
Ứng dụng[sửa | sửa mã nguồn]
Quang học có mặt trong đời sống hàng ngày. Hệ thống thị giác có mặt ở khắp nơi trong ngành sinh học cho thấy vai trò trung tâm của quang học như là khoa học của một trong năm giác quan. Nhiều người hưởng lợi từ việc đeo kính mắt hoặc kính áp tròng, và quang học được áp dụng để đưa ra nhiều hàng hóa tiêu dùng chất lượng như máy ảnh. Cầu vồng và ảnh mờ ảo (mirage) là các ví dụ cho hiện tượng quang học. Thông tin quang là nền tảng cho các công nghệ Internet và truyền thông.
Mắt người[sửa | sửa mã nguồn]

Một trong những chức năng của mắt người là tập trung ánh sáng lên một lớp các tế bào nhận kích thích ánh sáng gọi là võng mạc, lớp lót nằm phía trong cầu mắt. Sự tập trung được thực hiện bởi một loạt các môi trường trong suốt. Ánh sáng đi vào mắt đi qua môi trường đầu tiên là giác mạc, nó mang lại nhiều công suất quang học của mắt. Ánh sáng tiếp tục đi qua một chất lỏng nằm ngay phía sau giác mạc—khoang phía trước (anterior chamber), rồi đi qua đồng tử. Tiếp đó ánh sáng đi qua thủy tinh thể, cho phép tập trung thêm ánh sáng và điều chỉnh khả năng nhìn gần hay xa của mắt. Sau đó ánh sáng đi qua chất lỏng chứa chủ yếu trong cầu mắt là thủy dịch (vitreous humour), rồi tới võng mạc. Các tế bào nằm phần lớn trong võng mạc nằm ngay sau mắt, ngoại trừ vị trí có dây thần kinh thị giác; hay chính là điểm mù.
Có hai loại tế bào nhận kích thích ánh sáng, đó là tế bào hình nón và tế bào hình que, chúng có độ nhạy khác nhau đối với các loại ánh sáng khác nhau.[77] Tế bào hình que nhạy đối với cường độ ánh sáng trong phạm vi rộng của tần số, do vậy chịu trách nhiệm đối với thị giác đen và trắng (nhìn ban đêm). Tế bào hình que không có tại điểm vàng, vùng võng mạc chịu trách nhiệm cho thị giác trung tâm, và không đáp ứng được đối với sự thay đổi về không gian và thời gian của ánh sáng như tế bào hình nó. Tuy nhiên, số lượng tế bào hình que nhiều hơn 20 lần tế bào hình nón trong võng mạc bởi vì tế bào hình que phân bố trên phạm vi rộng hơn. Nhờ phân bố rộng hơn, tế bào hình que chịu trách nhiệm cho thị giác ngoại biên (peripheral vision).[78]
Ngược lại, các tế bào hình nón ít nhạy sáng hơn, nhưng chúng nhạy chủ yếu đối với ba loại dải tần số ánh sáng khác nhau và do đó có chức năng cảm nhận màu sắc và độ chói (photopic vision). Tế bào hình nón tập trung chủ yếu ở điểm vàng và rất nhạy với độ tinh của màu sắc do đó chúng cho phép phân biệt không gian tốt hơn so với tế bào hình que. Vì tế bào hình nón không nhạy đối với ánh sáng mờ tối bằng tế bào hình que, phần lớn khả năng nhìn ban đêm là ở tế bào hình que. Mặt khác, do các tế bào hình nón tập trung ở điểm vàng, thị giác trung tâm (bao gồm khả năng nhìn để đọc, để thấy các chi tiết nhỏ như xâu kim, hoặc kiểm tra vật thể) là do các tế bào hình nón.[78]
Cơ mi bao xung quanh thủy tinh thể cho phép sự tập trung ánh sáng của mắt có thể điều chỉnh được, hay quá trình điều tiết. Điểm gần và điểm xa xác định khoảng cách gần nhất và xa nhất từ mắt mà ảnh một vật thể hiện rõ nét trên võng mạc. Đối với một người có khả năng nhìn thông thường, điểm xa nằm ở vô tận. Vị trí của điểm gần phụ thuộc vào khả năng cơ mi có thể làm tăng độ cong của thủy tinh thể, và độ đàn hồi của thủy tinh thể ảnh hưởng bởi tuổi tác. Các bác sĩ chuyên khoa mắt (optometrist), nhà khoa học nhãn khoa (ophthalmologist), và nhà quang học thường coi một điểm gần là điểm nằm gần hơn khoảng cách mà mắt có thể đọc một cách bình thường—xấp xỉ bằng 25 cm.[77]
Thị lực có thể giải thích nhờ các nguyên lý quang học. Khi con người trở lên già đi, thủy tinh thể trở lên kém đàn hồi và điểm gần dần lùi xa khỏi mắt, một tật gọi là lão thị. Tương tự, những người mắc chứng viễn thị không thể giảm tiêu cự của thủy tinh thể cho phép thu được ảnh các vật ở gần trên võng mạc của họ. Ngược lại, những người không thể làm tăng tiêu cự thủy tinh thể đủ để ảnh của các vật ở xa tập trung rõ tại võng mạc hay họ mắc chứng cận thị và điểm xa có khoảng cách hữu hạn hơn là khoảng cách vô hạn đối với mắt bình thường. Một tật khác đó là loạn thị khi giác mạc không có dạng cầu nhưng bị cong nhiều hơn về một hướng. Điều này khiến cho những vật có bề ngang lớn bị tập trung trên nhiều phần khác nhau của võng mạc so với những vật có kích thước ngang hẹp, và kết quả là ảnh của vật bị méo mó.[77]
Những tật về mắt kể trên có thể khắc phục bằng cách sử dụng dụng cụ thấu kính hiệu chỉnh (corrective lens). Đối với viễn thị và lão thị, kính mắt dạng thấu kính hội tụ giúp điểm gần nằm gần hơn về mắt trong khi thấu kính phân kỳ giúp mắt cận thị đưa điểm xa trở thành điểm nằm ở vô tận. Người loạn thị được đeo kính có bề mặt hình trụ giúp bù lại sự không đồng đều của sự phân bố tia sáng trên võng mạc.[79]
Công suất quang học của kính hiệu chỉnh được đo bằng đi ốp (diopter), giá trị bằng nghịch đảo của tiêu cự đo theo đơn vị mét; với giá trị dương tương ứng với thấu kính hội tụ và giá trị âm tương ứng với thấu kính phân kỳ. Đối với kính dùng cho người loạn thị, có ba thông số cho mắt kính: một cho công suất hình cầu, một cho công suất hình trụ, và một cho góc của hướng loạn thị.[79]
Hiệu ứng thị giác[sửa | sửa mã nguồn]

Ảo ảnh quang học (còn gọi là ảo ảnh thị giác) là một đặc điểm do nhận thức của thị giác về hình ảnh khác so với đối tượng thực. Thông tin thu nhận bởi mắt được chuyển thành các tín hiệu về não bộ xử lý để cho cảm nhận về vật được quan sát. Có nhiều hiện tượng tạo ra ảo ảnh quang học bao gồm hiệu ứng vật lý tạo ra ảnh khác so với vật thực, hoặc hiệu ứng thần kinh và sinh lý tác động bởi mắt và não/hệ thần kinh (như độ sáng, màu sắc, chuyển động, nằm nghiêng, quay tròn), và ảo ảnh nhận thức khi não dựa trên các thông tin từ mắt đưa ra kết luận không nhận thức được.[80]
Ảo ảnh nhận thức cũng bao gồm kết quả từ việc không nhận thức được sự áp dụng sai các nguyên lý quang học. Ví dụ, phòng Ames, ảo ảnh Hering, Müller-Lyer, Orbison, Ponzo, Sander, và ảo ảnh Wundt tất cả dựa trên cảm nhận về khoảng cách khi vẽ ra các đường hội tụ hay phân kỳ, theo cách giống với các tia sáng song song (hoặc thực sự là các đường thẳng song song) hiện lên như đang hội tụ tại một điểm nằm ở vô tận trong hình ảnh phối cảnh hai chiều.[81] Hiệu ứng này cũng giải thích cho nghịch lý nổi tiếng là ảo ảnh Mặt Trăng khi Mặt Trăng dường như trông to hơn khi nó ở gần chân trời so với khi nó ở thiên đỉnh.[82] Ptolemy đã sai khi giải thích ảo ảnh này là do sự khúc xạ khí quyển khi ông miêu tả hiện tượng này trong cuốn Optics.[8]
Những kiểu ảo ảnh khác áp dụng thủ thuật các mảnh bị phá vỡ để đánh lừa cảm nhận về sự đối xứng hoặc sự bất đối xứng của vật thể. Ví như ảo ảnh tường café, Ehrenstein, ảo ảnh xoắn ốc Fraser, ảo ảnh Poggendorff, và ảo ảnh Zöllner. Có một sự liên quan, nhưng không chỉ là ảo ảnh, đó là cấu trúc lặp đi lặp lại hoặc chồng chập của các thành phần. Ví dụ các dải mỏng trong suốt xếp thành hình cấu trúc lưới như mẫu moiré, trong khi các phần trong suốt tuần hoàn kết hợp lại tạo thành các đường hoặc cung tối như đường moiré.[83]
Dụng cụ quang học[sửa | sửa mã nguồn]
Các thấu kính đơn lẻ có nhiều ứng dụng khác nhau như thấu kính máy ảnh, thấu kính hiệu chỉnh, và kính lúp trong khi các gương đơn sử dụng như gương parabol và gương chiếu hậu. Bằng cách kết hợp một số loại gương, lăng kính, và thấu kính tạo ra tổ hợp dụng cụ quang học cho phép mở rộng khả năng của từng dụng cụ. Ví dụ, kính tiềm vọng đơn giản chỉ bao gồm hai gương phẳng sắp thẳng hàng cho phép quan sát tránh khỏi vật cản trở. Những dụng cụ quang học nổi tiếng nhất trong khoa học là kính hiển vi quang học và kính thiên văn quang học mà cả hai được người Hà Lan phát minh ra vào cuối thế kỷ 16.[84]
Những kính hiển vi đầu tiên chi có hai thấu kính: một vật kính và một thị kính. Vật kính được làm với tiêu cự rất ngắn có chức năng phóng đại ảnh của vật trong khi nói chung thị kính có tiêu cự lớn hơn. Điều này giúp cho thị kính tạo thêm ảnh phóng đại khi ảnh qua vật kính nằm gần vật được quan sát. Ngoài ra kính hiển vi cần thêm một nguồn chiếu sáng do ảnh phóng đại thường bị mờ do định luật bảo toàn năng lượng và sự phân tán chùm sáng ra một bề mặt diện tích lớn hơn. Kính hiển vi hiện đại, hay kính hiển vi tổ hợp có nhiều thấu kính kết hợp với nhau (thường là bốn) để tối ưu hóa chức năng và nâng cao sự ổn định của ảnh.[84] Một biến thể khác của kính hiển vi, kính hiển vi so sánh, dùng để nhìn vào vật dưới những góc khác nhau và tạo ra ống nhòm lập thể cho ảnh 3 chiều của vật.[85] Ngày nay có rất nhiều loại kính hiển vi khác nhau, dựa trên những nguyên lý của cơ học lượng tử cho phép có độ phân giải vượt qua giới hạn phân giải quang học.
Kính thiên văn đầu tiên, gọi là kính thiên văn khúc xạ cũng chỉ bao gồm một vật kính và thị kính. Ngược lại so với kính hiển vi, vật kính của kính thiên văn được thiết kế có tiêu cự lớn để tránh được quang sai. Vật kính tập trung hình ảnh của một vật ở xa tại tiêu điểm của nó mà được điều chỉnh sao cho nó nằm tại tiêu điểm của thị kính có tiêu cự ngắn hơn. Mục đích chính của kính thiên văn là tập trung càng nhiều ánh sáng đến từ vật thể ở xa càng tốt và điều này xác định bởi độ lớn của vật kính. Do vậy, kính thiên văn thường được thể hiện bằng đường kính của vật kính hơn là độ phóng đại của nó do độ phóng đại có thể thay đổi nhờ cách thay thị kính. Bởi vì độ phóng đại của kính thiên văn khúc xạ bằng tiêu cự của vật kính chia cho tiêu cự của thị kính, thị kính càng có tiêu cự nhỏ thì càng cho độ phóng đại lớn, mặc dù nó cũng có giới hạn riêng.[84]
Vì sản xuất ra thấu kính đường kính lớn khó hơn nhiều so với chế tạo gương lớn, hầu hết kính thiên văn hiện đại ngày nay là kính thiên văn phản xạ, tức là kính thiên văn có gương cong lớn chứ không phải là thấu kính. Và tương tự, kính thiên văn phản xạ càng có đường kính gương chính lớn thì càng thu nhận được nhiều ánh sáng và độ phóng đại vẫn bằng tiêu cự của gương chính chia cho tiêu cự của thị kính. Các kính thiên văn hiện đại được bố trí nhiều gương chính và gương phụ cũng như các thiết bị cảm biến đo lường hơn là thị kính nằm tại tiêu điểm của thiết bị (như CCD).[84]
Nhiếp ảnh[sửa | sửa mã nguồn]


Lĩnh vực quang học của nhiếp ảnh bao gồm thấu kính máy ảnh và môi trường trên đó bức xạ điện từ được ghi lại, có thể là tấm âm bản, phim âm bản hay CCD. Nhiếp ảnh gia phải xét đến quy luật tương hỗ của máy ảnh và thời gian chụp mà có liên hệ sau
- Độ phơi sáng ∝ Diện tích độ mở × Thời gian phơi sáng × Độ sáng cảnh chụp[86]
Nghĩa là, độ mở càng nhỏ (cho độ sâu/mức tập trung của ảnh hơn), ánh sáng đến càng ít, do vậy thời gian phơi sáng phải tăng lên (dẫn đến khả năng ảnh bị nhòe nếu có chuyển động). Ví dụ của luật tương hỗ đó là quy tắc f/16 chụp trong ngày nắng đưa ra ước lượng thô cho các thiết lập cần thiết để có độ phơi sáng thông thường chụp vào ban ngày.[87]
Độ mở của máy ảnh đo bằng đại lượng không thứ nguyên f-số, f/#, thường ký hiệu là , and given by
với là tiêu cự, và là đường kính lỗ máy ảnh. Theo quy ước, "f/#" được coi như bằng một ký hiệu, và giá trị cụ thể của f/# được viết bằng cách thay # bằng giá trị số. Có hai cách để tăng f/# là hoặc giảm đường kính của lỗ mở hoặc tăng độ lớn của tiêu cự (trong trường hợp của thấu kính điều chỉnh (ống kính zoom), điều này được thực hiện đơn giản bằng cách điều chỉnh thấu kính). Giá trị f-số cao hơn cũng có nghĩa là độ sâu trường ảnh lớn hơn do thấu kính tiếp cận giới hạn của một máy ảnh đục lỗ (pinhole camera) mà có thể tập trung mọi ảnh một cách hoàn hảo, bất kể khoảng cách, nhưng đòi hỏi thời gian phơi sáng lâu.[88]
Trường nhìn của thấu kính thay đổi theo tiêu cự của thấu kính. Có ba cách phân loại cơ bản dựa trên mối liên hệ giữa kích thước theo đường chéo của phim âm bản hoặc kích cỡ của cảm biến đối với tiêu cự của thấu kính:[89]
- Ống kính thường: góc chụp vào khoảng 50° (gọi là thường bởi vì góc này thường là bằng độ rộng tầm nhìn của mắt người[89]) và tiêu cự xấp xỉ bằng đường chéo của phim âm bản hoặc của cảm biến.[90]
- Ống kính góc rộng: góc chụp lớn hơn 60° và tiêu cự ngắn hơn ống kính thường.[91]
- Ống kính te le: góc chụp nhỏ hơn so với ống kính thường. Các ống kính này có tiêu cự lớn hơn kích thước đường chéo của phim âm bản hay cảm biến CCD.[92] Loại ống kính có tiêu cự lớn phổ biến là ống kính tele, thiết kế sử dụng các thấu kính cho phép tiêu cự tổng hợp ngắn hơn tiêu cự của từng thấu kính.[93]
Các ống kính zoom hiện đại có thể có đặc tính của ba loại ống kính trên.
Giá trị tuyệt đối cho thời gian phơi sáng đòi hỏi phụ thuộc vào độ nhạy ánh sáng của phim âm bản hay cảm biến CCD (đo bởi tốc độ nhạy của phim, hay đối với cảm biến hiện đại đo bằng hiệu suất lượng tử).[94] Thời buổi đầu của nhiếp ảnh, các nhiếp ảnh gia sử dụng các tấm phim âm bản có độ nhạy sáng thấp, do vậy thời gian phơi sáng cũng cần phải dài ngay cả với lần chụp có hỗ trợ của nguồn sáng mạnh. Với sự phát triển của công nghệ, độ nhạy của phim và cảm biến đã được tăng lên đáng kể.[95]
Những kết quả khác từ quang hình học và quang học vật lý cũng áp dụng cho quang học máy ảnh. Ví dụ, khả năng phân giải lớn nhất của một cấu hình camera được xác định bởi giới hạn nhiễu xạ gắn liền với độ rộng của lỗ máy ảnh, hay giới hạn Rayleigh.[96]
Quang học khí quyển[sửa | sửa mã nguồn]

Các tính chất quang học độc nhất của khí quyển làm xuất hiện một số các hiện tượng quang học kỳ thú trên thế giới. Màu xanh của nền trời là kết quả trực tiếp của hiện tượng tán xạ Rayleigh làm lệch hướng mạnh các tia sáng có tần số cao (lam) trở lại trường nhìn của người quan sát. Bởi vì ánh sáng xanh da trời bị tán xạ dễ dàng hơn ánh sáng đỏ, Mặt Trời có màu hơi đỏ khi quan sát nó qua lớp khí quyển dày, tại thời điểm Mặt Trời mọc hay Mặt Trời lặn. Nếu có thêm những loại hạt bụi hoặc khí đặc biệt trong khí quyển có thể làm tán xạ tia sáng Mặt Trời ở những góc khác nhau tạo ra bầu trời đầy màu sắc vào thời điểm bình minh hoặc chạng vạng. Các tinh thể băng và các hạt bụi khác trong khí quyển là nguyên nhân tạo ra các hiện tượng như hào quang, ánh hồng ban chiều (afterglow), nhật hoa, tia sáng xuyên mây, và Mặt Trời giả. Sự xuất hiện đa dạng của những hiện tượng này là do kích cỡ khác nhau của các hạt bụi và sự phân bố của chúng trong khí quyển.[97]
Ảo tượng (mirage) là hiện tượng quang học trong đó các tia sáng bị lệch do sự thăng giáng nhiệt trong chỉ số khúc xạ của không khí, tạo ra sự dời ảnh hoặc ảnh bị méo của các vật thể ở xa. Những hiện tượng quang học khác kết hợp với hiện tượng này là hiệu ứng Novaya Zemlya khi Mặt Trời trông như có vẻ mọc sớm hơn so với dự định do hình ảnh méo của nó. Một dạng ảo ảnh kỳ lạ khác kết hợp với hiệu ứng nghịch đảo nhiệt (temperature inversion) là ảo ảnh Fata Morgana khi các vật ở chân trời hoặc thậm chí vượt xa chân trời, như đảo, vách núi, tàu thuyền hay băng trôi dường như bị kéo giãn và nâng lên khỏi chân trời, trông giống như "lâu đài trong cổ tích".[98]
Cầu vồng là kết quả của sự kết hợp giữa phản xạ và khúc xạ tia sáng qua các hạt mưa hoặc hơi nước. Phản xạ của tia sáng qua các hạt mưa tạo ra đường kính góc của một cầu vồng trên bầu trời vào khoảng 40° đến 42° với vòng đỏ nằm ngoài cùng. Hiện tượng cầu vồng đôi xảy ra khi hai tia phản xạ tạo ra đường kính góc là 50,5° đến 54° đối với ánh sáng tím nằm bên ngoài. Bởi vì cầu vồng nhìn thấy ở hướng ngược 180° tính từ tâm cầu vồng so với Mặt Trời, cầu vồng càng rõ khi Mặt Trời ở gần chân trời.[64]
Chú thích[sửa | sửa mã nguồn]
- ^ a b McGraw-Hill Encyclopedia of Science and Technology (ấn bản 5). McGraw-Hill. 1993.
- ^ “World's oldest telescope?”. BBC News. ngày 1 tháng 7 năm 1999. Truy cập 3 tháng 1 năm 2010.
- ^ T. F. Hoad (1996). The Concise Oxford Dictionary of English Etymology. ISBN 0-19-283098-8.
- ^ A History Of The Eye. stanford.edu. Truy cập 2012-06-10.
- ^ T. L. Heath (2003). A manual of greek mathematics. Courier Dover Publications. tr. 181–182. ISBN 0-486-43231-9.
- ^ William R. Uttal (1983). Visual Form Detection in 3-Dimensional Space. Psychology Press. tr. 25–. ISBN 978-0-89859-289-4. Bản gốc lưu trữ ngày 5 tháng 7 năm 2014. Truy cập ngày 3 tháng 11 năm 2014.
- ^ Euclid (1999). Elaheh Kheirandish (biên tập). The Arabic version of Euclid's optics = Kitāb Uqlīdis fī ikhtilāf al-manāẓir. New York: Springer. ISBN 0-387-98523-9.
- ^ a b Ptolemy (1996). A. Mark Smith (biên tập). Ptolemy's theory of visual perception: an English translation of the Optics with introduction and commentary. DIANE Publishing. ISBN 0-87169-862-5.
- ^ Adamson, Peter (2006). "Al-Kindi¯ and the reception of Greek philosophy". In Adamson, Peter; Taylor, R.. The Cambridge companion to Arabic philosophy. Cambridge University Press. p. 45. ISBN 978-0-521-52069-0.
- ^ a b Rashed, Roshdi (1990). “A pioneer in anaclastics: Ibn Sahl on burning mirrors and lenses”. Isis. 81 (3): 464–491. doi:10.1086/355456. JSTOR 233423.
- ^ A. I. Sabra and J. P. Hogendijk (2003). The Enterprise of Science in Islam: New Perspectives. MIT Press. tr. 85–118. ISBN 0-262-19482-1. OCLC 237875424.
- ^ G. Hatfield (1996). “Was the Scientific Revolution Really a Revolution in Science?”. Trong F. J. Ragep, P. Sally, S. J. Livesey (biên tập). Tradition, Transmission, Transformation: Proceedings of Two Conferences on Pre-modern Science held at the University of Oklahoma. Brill Publishers. tr. 500. ISBN 9004101195.Quản lý CS1: nhiều tên: danh sách biên tập viên (liên kết)
- ^ Nader El-Bizri (2005). “A Philosophical Perspective on Alhazen's Optics”. Arabic Sciences and Philosophy. 15: 189–218. doi:10.1017/S0957423905000172.
- ^ Nader El-Bizri (2007). “In Defence of the Sovereignty of Philosophy: al-Baghdadi's Critique of Ibn al-Haytham's Geometrisation of Place”. Arabic Sciences and Philosophy. 17: 57–80. doi:10.1017/S0957423907000367.
- ^ G. Simon (2006). “The Gaze in Ibn al-Haytham”. The Medieval History Journal. 9: 89. doi:10.1177/097194580500900105.
- ^ Ian P. Howard; Brian J. Rogers (1995). Binocular Vision and Stereopsis. Oxford University Press. tr. 7. ISBN 978-0-19-508476-4.
- ^ Elena Agazzi; Enrico Giannetto; Franco Giudice (2010). Representing Light Across Arts and Sciences: Theories and Practices. V&R unipress GmbH. tr. 42. ISBN 978-3-89971-735-8.
- ^ D. C. Lindberg, Theories of Vision from al-Kindi to Kepler, (Chicago: Univ. of Chicago Pr., 1976), pp. 94–99.
- ^ Vincent, Ilardi (2007). Renaissance Vision from Spectacles to Telescopes. Philadelphia, PA: American Philosophical Society. tr. 4–5. ISBN 9780871692597.
- ^ '''The Galileo Project > Science > The Telescope''' by Al Van Helden ''. Galileo.rice.edu. Truy cập 2012-06-10.
- ^ Henry C. King (2003). The History of the Telescope. Courier Dover Publications. tr. 27. ISBN 978-0-486-43265-6.
- ^ Paul S. Agutter; Denys N. Wheatley (2008). Thinking about Life: The History and Philosophy of Biology and Other Sciences. Springer. tr. 17. ISBN 978-1-4020-8865-0.
- ^ Vincent Ilardi (2007). Renaissance Vision from Spectacles to Telescopes. American Philosophical Society. tr. 210. ISBN 978-0-87169-259-7.
- ^ Microscopes: Time Line, Nobel Foundation, retrieved ngày 3 tháng 4 năm 2009
- ^ Fred Watson (2007). Stargazer: The Life and Times of the Telescope. Allen & Unwin. tr. 55. ISBN 978-1-74175-383-7.
- ^ Vincent Ilardi (2007). Renaissance Vision from Spectacles to Telescopes. American Philosophical Society. tr. 244. ISBN 978-0-87169-259-7.
- ^ Caspar, Kepler, pp. 198–202, Courier Dover Publications, 1993, ISBN 0486676056.
- ^ a b A. I. Sabra (1981). Theories of light, from Descartes to Newton. CUP Archive. ISBN 0-521-28436-8.
- ^ W. F. Magie (1935). A Source Book in Physics. Harvard University Press. tr. 309.
- ^ J. C. Maxwell (1865). “A Dynamical Theory of the Electromagnetic Field”. Philosophical Transactions of the Royal Society of London. 155: 459. Bibcode:1865RSPT..155..459C. doi:10.1098/rstl.1865.0008.
- ^ For a solid approach to the complexity of Planck's intellectual motivations for the quantum, for his reluctant acceptance of its implications, see H. Kragh, Max Planck: the reluctant revolutionary Lưu trữ 2012-04-01 tại Wayback Machine, Physics World. December 2000.
- ^ Einstein, A. (1967). “On a heuristic viewpoint concerning the production and transformation of light”. Trong Ter Haar, D. (biên tập). The Old Quantum Theory (PDF). Pergamon. tr. 91–107. Truy cập ngày 18 tháng 3 năm 2010.[liên kết hỏng] The chapter is an English translation of Einstein's 1905 paper on the photoelectric effect.
- ^ Einstein, A. (1905). “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt” [On a heuristic viewpoint concerning the production and transformation of light]. Annalen der Physik (bằng tiếng Đức). 322 (6): 132–148. Bibcode:1905AnP...322..132E. doi:10.1002/andp.19053220607.
- ^ “On the Constitution of Atoms and Molecules”. Philosophical Magazine. 26, Series 6: 1–25. 1913. Bản gốc lưu trữ ngày 4 tháng 7 năm 2007. Truy cập ngày 3 tháng 11 năm 2014.. The landmark paper laying the Bohr model of the atom and molecular bonding.
- ^ R. Feynman (1985). “Chapter 1”. QED: The Strange Theory of Light and Matter. Princeton University Press. tr. 6. ISBN 0-691-08388-6.
- ^ N. Taylor (2000). LASER: The inventor, the Nobel laureate, and the thirty-year patent war. New York: Simon & Schuster. ISBN 0-684-83515-0.
- ^ Ariel Lipson; Stephen G. Lipson; Henry Lipson (ngày 28 tháng 10 năm 2010). Optical Physics. Cambridge University Press. tr. 48. ISBN 978-0-521-49345-1. Truy cập ngày 12 tháng 7 năm 2012.
- ^ Sir Arthur Schuster (1904). An Introduction to the Theory of Optics. E. Arnold. tr. 41.
- ^ J. E. Greivenkamp (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. tr. 19–20. ISBN 0-8194-5294-7.
- ^ a b c d e f g h i j H. D. Young (1992). “35”. University Physics 8e. Addison-Wesley. ISBN 0-201-52981-5.
- ^ E. W. Marchand, Gradient Index Optics, New York, NY, Academic Press, 1978.
- ^ a b c d e f g h i j k l m E. Hecht (1987). Optics (ấn bản 2). Addison Wesley. ISBN 0-201-11609-X. Chapters 5 & 6.
- ^ MV Klein & TE Furtak, 1986, Optics, John Wiley & Sons, New York ISBN 0471872970.
- ^ Maxwell, James Clerk (1865). “A dynamical theory of the electromagnetic field” (PDF). Philosophical Transactions of the Royal Society of London. 155: 499. doi:10.1098/rstl.1865.0008. This article accompanied a ngày 8 tháng 12 năm 1864 presentation by Maxwell to the Royal Society. See also A dynamical theory of the electromagnetic field.
- ^ M. Born and E. Wolf (1999). Principle of Optics. Cambridge: Cambridge University Press. ISBN 0-521-64222-1.
- ^ J. Goodman (2005). Introduction to Fourier Optics (ấn bản 3). Roberts & Co Publishers. ISBN 0-9747077-2-4.
- ^ A. E. Siegman (1986). Lasers. University Science Books. ISBN 0-935702-11-3. Chapter 16.
- ^ a b c d H. D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0-201-52981-5.Chapter 37
- ^ a b P. Hariharan (2003). Optical Interferometry (PDF) (ấn bản 2). San Diego, USA: Academic Press. ISBN 0-12-325220-2.
- ^ E. R. Hoover (1977). Cradle of Greatness: National and World Achievements of Ohio's Western Reserve. Cleveland: Shaker Savings Association.
- ^ J. L. Aubert (1760). Memoires pour l'histoire des sciences et des beaux arts. Paris: Impr. de S. A. S.; Chez E. Ganeau. tr. 149.
- ^ D. Brewster (1831). A Treatise on Optics. London: Longman, Rees, Orme, Brown & Green and John Taylor. tr. 95.
- ^ R. Hooke (1665). Micrographia: or, Some physiological descriptions of minute bodies made by magnifying glasses. London: J. Martyn and J. Allestry. ISBN 0-486-49564-7.
- ^ H. W. Turnbull (1940–1941). “Early Scottish Relations with the Royal Society: I. James Gregory, F.R.S. (1638–1675)”. Notes and Records of the Royal Society of London. 3: 22. doi:10.1098/rsnr.1940.0003. JSTOR 531136.
- ^ T. Rothman (2003). Everything's Relative and Other Fables in Science and Technology. New Jersey: Wiley. ISBN 0-471-20257-6.
- ^ a b c d H. D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0-201-52981-5.Chapter 38
- ^ R. S. Longhurst (1968). Geometrical and Physical Optics, 2nd Edition. London: Longmans.
- ^ Lucky Exposures: Diffraction limited astronomical imaging through the atmosphere by Robert Nigel Tubbs
- ^ C. F. Bohren and D. R. Huffman (1983). Absorption and Scattering of Light by Small Particles. Wiley. ISBN 0-471-29340-7.
- ^ a b J. D. Jackson (1975). Classical Electrodynamics (ấn bản 2). Wiley. tr. 286. ISBN 0-471-43132-X.
- ^ a b R. Ramaswami and K. N. Sivarajan (1998). Optical Networks: A Practical Perspective. London: Academic Press. ISBN 0123740924.
- ^ Brillouin, Léon. Wave Propagation and Group Velocity. Academic Press Inc., New York (1960)
- ^ M. Born and E. Wolf (1999). Principle of Optics. Cambridge: Cambridge University Press. tr. 14–24. ISBN 0-521-64222-1.
- ^ a b c d e f H. D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0-201-52981-5.Chapter 34
- ^ F. J. Duarte (2003). Tunable Laser Optics. New York: Elsevier-Academic. tr. 87–90. ISBN 0-12-222696-8.
- ^ D. F. Walls and G. J. Milburn Quantum Optics (Springer 1994)
- ^ Alastair D. McAulay (ngày 16 tháng 1 năm 1991). Optical computer architectures: the application of optical concepts to next generation computers. Wiley. ISBN 978-0-471-63242-9. Truy cập ngày 12 tháng 7 năm 2012.
- ^ Y. R. Shen (1984). The principles of nonlinear optics. New York, Wiley-Interscience. ISBN 0-471-88998-9.
- ^ “laser”. Reference.com. Truy cập ngày 15 tháng 5 năm 2008.
- ^ Charles H. Townes – Nobel Lecture. nobelprize.org
- ^ “The VLT's Artificial Star”. ESO Picture of the Week. Truy cập ngày 25 tháng 6 năm 2014.
- ^ C. H. Townes. “The first laser”. University of Chicago. Truy cập ngày 15 tháng 5 năm 2008.
- ^ C. H. Townes (2003). “The first laser”. Trong Laura Garwin and Tim Lincoln (biên tập). A Century of Nature: Twenty-One Discoveries that Changed Science and the World. University of Chicago Press. tr. 107–12. ISBN 0-226-28413-1. Truy cập ngày 2 tháng 2 năm 2008.
- ^ What is a bar code? denso-wave.com
- ^ “How the CD was developed”. BBC News. ngày 17 tháng 8 năm 2007. Truy cập ngày 17 tháng 8 năm 2007.
- ^ J. Wilson and J.F.B. Hawkes (1987). Lasers: Principles and Applications, Prentice Hall International Series in Optoelectronics. Prentice Hall. ISBN 0-13-523697-5.
- ^ a b c D. Atchison and G. Smith (2000). Optics of the Human Eye. Elsevier. ISBN 0-7506-3775-7.
- ^ a b E. R. Kandel, J. H. Schwartz, T. M. Jessell (2000). Principles of Neural Science (ấn bản 4). New York: McGraw-Hill. tr. 507–513. ISBN 0-8385-7701-6.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
- ^ a b D. Meister. “Ophthalmic Lens Design”. OptiCampus.com. Truy cập ngày 12 tháng 11 năm 2008.
- ^ J. Bryner (ngày 2 tháng 6 năm 2008). “Key to All Optical Illusions Discovered”. LiveScience.com.
- ^ Geometry of the Vanishing Point Lưu trữ 2008-06-22 tại Wayback Machine at Convergence Lưu trữ 2006-02-12 tại Wayback Machine
- ^ "The Moon Illusion Explained" Lưu trữ 2015-12-04 tại Wayback Machine, Don McCready, University of Wisconsin-Whitewater
- ^ A. K. Jain, M. Figueiredo, J. Zerubia (2001). Energy Minimization Methods in Computer Vision and Pattern Recognition. Springer. ISBN 978-3-540-42523-6.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
- ^ a b c d H. D. Young (1992). “36”. University Physics 8e. Cornell University. ISBN 0-201-52981-5.
- ^ P. E. Nothnagle, W. Chambers, M. W. Davidson. “Introduction to Stereomicroscopy”. Nikon MicroscopyU.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
- ^ Samuel Edward Sheppard and Charles Edward Kenneth Mees (1907). Investigations on the Theory of the Photographic Process. Longmans, Green and Co. tr. 214.
- ^ B. J. Suess (2003). Mastering Black-and-White Photography. Allworth Communications. ISBN 1-58115-306-6.
- ^ M. J. Langford (2000). Basic Photography. Focal Press. ISBN 0-240-51592-7.
- ^ a b Bruce Warren (2001). Photography. Cengage Learning. tr. 71. ISBN 978-0-7668-1777-7.
- ^ Leslie D. Stroebel (1999). View Camera Technique. Focal Press. ISBN 0-240-80345-0.
- ^ S. Simmons (1992). Using the View Camera. Amphoto Books. tr. 35. ISBN 0-8174-6353-4.
- ^ Sidney F. Ray (2002). Applied Photographic Optics: Lenses and Optical Systems for Photography, Film, Video, Electronic and Digital Imaging. Focal Press. tr. 294. ISBN 978-0-240-51540-3.
- ^ New York Times Staff (2004). The New York Times Guide to Essential Knowledge. Macmillan. ISBN 978-0-312-31367-8.
- ^ R. R. Carlton, A. McKenna Adler (2000). Principles of Radiographic Imaging: An Art and a Science. Thomson Delmar Learning. ISBN 0-7668-1300-2.
- ^ W. Crawford (1979). The Keepers of Light: A History and Working Guide to Early Photographic Processes. Dobbs Ferry, New York: Morgan & Morgan. tr. 20. ISBN 0-87100-158-6.
- ^ J. M. Cowley (1975). Diffraction physics. Amsterdam: North-Holland. ISBN 0-444-10791-6.
- ^ C. D. Ahrens (1994). Meteorology Today: an introduction to weather, climate, and the environment (ấn bản 5). West Publishing Company. tr. 88–89. ISBN 0-314-02779-3.
- ^ A. Young. “An Introduction to Mirages”.
Thư mục tham khảo[sửa | sửa mã nguồn]
- Born, Max; Wolf, Emil (2002). Principles of Optics. Cambridge University Press. ISBN 1139643401.
- Hecht, Eugene (2002). Optics (4 ed.). Addison-Wesley Longman, Incorporated. ISBN 0805385665.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for scientists and engineers (6, illustrated ed.). Belmont, CA: Thomson-Brooks/Cole. ISBN 0534408427.
- Tipler, Paul A.; Mosca, Gene (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics 2. W. H. Freeman. ISBN 9780716708100.
- Lipson, Stephen G.; Lipson, Henry; Tannhauser, David Stefan (1995). Optical Physics. Cambridge University Press. ISBN 0521436311.
- Fowles, Grant R. (1975). Introduction to Modern Optics. Courier Dover Publications. ISBN 0486659577.
Liên kết ngoài[sửa | sửa mã nguồn]
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Quang học. |
- Thảo luận liên quan
- Optics trên chương trình In Our Time của BBC. (Nghe tại đây)
- Sách và hướng dẫn
- Optics Lưu trữ 2005-06-22 tại Wayback Machine – an open-source optics textbook
- Optics2001 – Optics library and community
- Fundamental Optics Lưu trữ 2014-11-10 tại Wayback Machine – Melles Griot Technical Guide
- Physics of Light and Optics – Brigham Young University Undergraduate Book
- Đọc thêm
- Các hiệp hội


































