Photon
 Các hạt photon được phát ra bởi chùm tia laze màu lục lam phía bên ngoài, còn bên trong canxit là chùm tia laze màu cam và huỳnh quang của nó | |
| Cấu trúc | Hạt sơ cấp |
|---|---|
| Nhóm | Gauge boson |
| Tương tác cơ bản | Tương tác điện từ, Tương tác yếu (và Tương tác hấp dẫn) |
| Lý thuyết | Albert Einstein (1905) Cái tên "photon" thường được gán cho Gilbert N. Lewis (1926) |
| Ký hiệu | γ |
| Khối lượng | 0 (giá trị lý thuyết) < 1×10−18 eV/c2 (giới hạn thử nghiệm)[1] |
| Thời gian sống | Ổn định[1] |
| Điện tích | 0
< 1×10−35 e[1] |
| Màu tích | 0 |
| Spin | 1 |
| Số trạng thái spin | Hai: +1 ℏ, −1 ℏ |
| Tán xạ |
|---|
 |
Photon hay quang tử (tiếng Hy Lạp: φῶς, phōs, ánh sáng; tiếng Việt đọc là phô tông hay phô tôn) là một loại hạt cơ bản, đồng thời là hạt lượng tử của trường điện từ và ánh sáng cũng như mọi dạng bức xạ điện từ khác. Nó cũng là hạt tải lực của lực điện từ. Các hiệu ứng của lực điện từ có thể dễ dàng quan sát ở cả thang vi mô và vĩ mô do photon không có khối lượng nghỉ; và điều này cũng cho phép các tương tác cơ bản xảy ra được ở những khoảng cách rất lớn. Cũng giống như mọi hạt cơ bản khác, photon được miêu tả bởi cơ học lượng tử và biểu hiện lưỡng tính sóng hạt — chúng thể hiện các tính chất giống như của cả sóng và hạt. Ví dụ, một hạt photon có thể bị khúc xạ bởi một thấu kính hoặc thể hiện sự giao thoa giữa các sóng, nhưng nó cũng biểu hiện như một hạt khi chúng ta thực hiện phép đo định lượng về động lượng của nó.
Khái niệm hiện đại về photon đã được phát triển dần dần bởi Albert Einstein để giải thích các quan sát thực nghiệm mà không thể được giải thích thỏa đáng bởi mô hình sóng cổ điển của ánh sáng. Đặc biệt, mô hình photon đưa ra sự phụ thuộc của năng lượng ánh sáng vào tần số, và giải thích khả năng của vật chất và bức xạ đạt đến trạng thái cân bằng nhiệt động. Mô hình cũng đưa ra sự giải thích cho một số quan sát khác thường, bao gồm tính chất của bức xạ vật đen, mà một số nhà vật lý, điển hình nhất là Max Planck, đã từng giải thích bằng cách sử dụng các mô hình bán cổ điển, theo đó ánh sáng vẫn được miêu tả bằng các phương trình Maxwell, những ánh sáng phát ra hoặc hấp thụ từ vật thể bị lượng tử hóa. Mặc dù những mô hình bán cổ điển này đóng góp vào sự phát triển của cơ học lượng tử, những thí nghiệm sau này[2][3] đã công nhận giả thiết của Einstein rằng chính ánh sáng bị lượng tử hóa; và lượng tử của ánh sáng là các hạt photon.
Trong Mô hình chuẩn hiện đại của vật lý hạt, photon được miêu tả như là một hệ quả cần thiết của các định luật vật lý với tính đối xứng tại mỗi điểm trong không thời gian. Các tính chất nội tại của photon như điện tích, khối lượng và spin được xác định bởi tính chất của đối xứng gauge. Lý thuyết neutrino về ánh sáng với cố gắng miêu tả photon có cấu trúc thành phần, vẫn chưa có được một thành công nào đáng kể.
Khái niệm photon đã dẫn đến những phát triển vượt bậc trong vật lý lý thuyết cũng như thực nghiệm, như laser, ngưng tụ Bose–Einstein, lý thuyết trường lượng tử, và cách giải thích theo xác suất của cơ học lượng tử. Nó đã được áp dụng cho các lĩnh vực như quang hóa học (photochemistry), kính hiển vi có độ phân giải cao và các phép đo khoảng cách giữa các phân tử. Hiện nay, photon được nghiên cứu như một trong những phần tử của các máy tính lượng tử và cho những ứng dụng phức tạp trong thông tin quang như mật mã lượng tử (quantum cryptograpy).
Thuật ngữ[sửa | sửa mã nguồn]
Năm 1900 Max Planck đang nghiên cứu về bức xạ vật đen và đề xuất ra là năng lượng của sóng điện từ có thể được giải phóng ra theo những "gói" năng lượng; mà ông gọi chúng là những lượng tử. Sau đó, năm 1905 Albert Einstein đã tiến xa hơn bằng đề xuất rằng sóng điện từ chỉ có thể tồn tại trong những gói rời rạc này.[4] Ông gọi những gói sóng này là lượng tử ánh sáng (tiếng Đức: das Lichtquant). Tên gọi photon bắt nguồn từ tiếng Hy Lạp cho ánh sáng, φως (chuyển tự thành phôs), và đã được sử dụng[Ct 1] bởi nhà hóa lý Gilbert Lewis năm 1926, người đã đưa ra một lý thuyết suy đoán các photon có đặc điểm "không thể tạo ra hoặc bị phá hủy".[5] Mặc dù lý thuyết của Lewis chưa bao giờ được công nhận do nó mâu thuẫn với nhiều thí nghiệm, thuật ngữ photon do ông đưa ra đã nhanh chóng được các nhà vật lý sử dụng. Isaac Asimov đã công nhận Arthur Compton là người đưa ra định nghĩa lượng tử năng lượng gắn với photon vào năm 1927.[6][7]
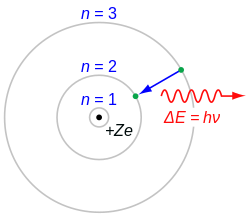
Trong vật lý học, photon thường được ký hiệu bởi chữ γ (chữ cái Hy Lạp gamma). Ký hiệu này có lẽ bắt nguồn từ tia gamma, do tia này được khám phá bởi Paul Villard năm 1900,[8][9] và được Ernest Rutherford đặt tên là tia gamma vào năm 1903, và sau đó Rutherford và Edward Andrade đã chỉ ra tia này là một dạng của bức xạ điện từ vào năm 1914.[10] Trong hóa học và kĩ thuật quang học, photon thường được ký hiệu là hν, hay đây là năng lượng của một photon, với h là hằng số Planck và chữ cái Hy Lạp ν (nu) là tần số của photon. Ít thông dụng hơn, photon có thể được ký hiệu là hf, trong đó tần số được ký hiệu bằng f.
Tính chất vật lý[sửa | sửa mã nguồn]
Photon là hạt phi khối lượng,[Ct 2] không có điện tích[11] và không bị phân rã tự phát trong chân không. Một photon có hai trạng thái phân cực và được miêu tả chính xác bởi ba tham số liên tục: là các thành phần của vectơ sóng của nó, xác định lên bước sóng λ và hướng lan truyền của photon. Photon là một boson gauge của trường điện từ,[12] và do vậy mọi số lượng tử khác của photon (như số lepton, số baryon, và số lượng tử hương) đều bằng 0.[13]

Các photon được phát ra từ rất nhiều quá trình trong tự nhiên. Ví dụ, khi một hạt tích điện bị gia tốc, nó sẽ phát ra bức xạ synchrotron. Trong quá trình một phân tử, nguyên tử hoặc hạt nhân trở về trạng thái có mức năng lượng thấp hơn, các photon với năng lượng khác nhau sẽ bị phát ra, từ bức xạ hồng ngoại cho đến tia gamma. Photon cũng được phát ra khi một hạt và phản hạt tương ứng hủy lẫn nhau (ví dụ như sự hủy cặp hạt electron và positron).
Trong chân không, photon chuyển động với vận tốc ánh sáng c và năng lượng cùng động lượng của nó được liên hệ trong công thức E = pc, với p là độ lớn của vector động lượng p. Công thức này suy ra từ công thức tương đối tính, với m = 0:[14]
Năng lượng và động lượng của photon chỉ phụ thuộc vào tần số (ν) của nó hay bước sóng (λ):
Với k là vectơ sóng (trong đó số sóng (wave number) k = |k| = 2π/λ), ω = 2πν là tần số góc, và ħ = h/2π là hằng số Planck thu gọn.[15]
Do p chỉ theo hướng của sự lan truyền photon, độ lớn của động lượng sẽ là
Photon cũng mang động lượng góc spin mà không phụ thuộc vào tần số của nó.[16] Độ lớn của spin là và thành phần đo dọc theo hướng chuyển động của nó, hay hình chiếu của động lượng (helicity), phải là ±ħ. Có hai hình chiếu của động lượng, gọi là bên phải (right-handed) và bên trái (left-handed), tương ứng với hai trạng thái phân cực tròn của photon.[17]
Để minh họa ý nghĩa của những công thức này, sự hủy của một hạt và phản hạt tương ứng trong chân không phải cho kết quả là tạo ra ít nhất hai photon vì những lý do sau. Đối với khối tâm của hệ, tổng động lượng toàn phần phải bằng không, trong khi đối với một photon thì nó luôn có động lượng (do những tính chất đã được miêu tả ở trước, động lượng chỉ phụ thuộc vào tần số hoặc bước sóng—mà không thể bằng không). Từ đó, theo định luật bảo toàn động lượng (hoặc tương đương với, bất biến tịnh tiến) đòi hỏi rằng ít nhất hai photon phải được tạo ra, cho tổng động lượng toàn phần bằng không. (Tuy vậy nếu hệ tương tác với một hạt khác hoặc một trường khác trong quá trình hủy cặp hạt thì có khả năng sinh ra một photon, ví dụ như khi một hạt positron hủy với một electron liên kết trong hệ nguyên tử, thì có thể sinh ra chỉ một photon do trường Coulomb của hạt nhân nguyên tử đã phá vỡ đối xứng tịnh tiến.) Năng lượng của hai photon, hay một cách tương đương, tần số của chúng, có thể được xác định từ định luật bảo toàn bốn-động lượng. Nhìn theo một hướng khác, ta có thể xem photon là phản hạt với chính nó. Và quá trình ngược lại, sự sinh cặp, thể hiện nổi bật trong cơ chế các hạt photon năng lượng cao như tia gamma bị mất năng lượng khi truyền qua vật chất.[18] Quá trình ngược lại của "sự hủy một hạt photon" được diễn ra trong điện trường của một hạt nhân nguyên tử.
Công thức cổ điển cho năng lượng và động lượng của bức xạ điện từ có thể được viết lại theo khái niệm của sự kiện photon. Ví dụ, áp suất bức xạ điện từ lên một vật được dẫn ra từ sự truyền động lượng của photon trên một đơn vị thời gian và một đơn vị diện tích của vật thể đó, do áp suất là lực trên một đơn vị diện tích và lực là sự thay đổi của động lượng trên đơn vị thời gian.[19]
Thí nghiệm kiểm tra khối lượng của photon[sửa | sửa mã nguồn]
Photon hiện tại được tin là không có khối lượng, nhưng nó vẫn còn là một câu hỏi trong lĩnh vực thực nghiệm. Nếu photon không phải là không có khối lượng, thì nó không thể chuyển động với vận tốc chính xác bằng vận tốc của ánh sáng trong chân không, c. Vận tốc của nó sẽ phải nhỏ hơn và phụ thuộc vào tần số của nó. Thuyết tương đối sẽ không bị ảnh hưởng bởi vấn đề này; vì cái gọi là vận tốc ánh sáng, c, do đó sẽ không phải là vận tốc thực mà ánh sáng di chuyển, mà là một hằng số của tự nhiên giới hạn vận tốc lớn nhất của bất kì một vật thể nào về mặt lý thuyết có thể đạt được trong không thời gian.[20] Và như thế, nó vẫn là vận tốc của những gợn không thời gian (các sóng hấp dẫn và các hạt graviton), nhưng nó không phải là vận tốc của photon.
Nếu hạt photon có khối lượng thì nó cũng sẽ ảnh hưởng đến tính chất khác. Như định luật Coulomb sẽ phải thay đổi và trường điện từ phải có thêm một bậc vật lý tự do. Những hiệu ứng này chi phối độ chính xác của các thí nghiệm nhằm khám phá khối lượng của photon cao hơn so với sự phụ thuộc vào tần số của vận tốc ánh sáng. Nếu định luật Coulomb không đúng hoàn toàn, thì nó sẽ khiến cho xuất hiện một điện trường bên trong một vật dẫn rỗng khi vật này được đặt trong một điện trường ngoài. Từ đây có thể kiểm tra định luật Coulomb với độ chính xác rất cao.[21] Thí nghiệm kiểm tra điều này không phát hiện ra được điện trường bên trong vật dẫn rỗng và đặt giới hạn cho khối lượng trên của photon trong thực nghiệm là m ≲ 10−14 eV/c2.[22]
Giới hạn trên cho khối lượng của photon với độ chính xác cao hơn thu được trong thí nghiệm nhằm xác định hiệu ứng gây nên bởi vectơ thế từ trường thiên hà (galactic vector magnetic potential). Mặc dù vectơ thế từ trường thiên hà là rất lớn do từ trường của thiên hà tồn tại trên những khoảng cách lớn, thì từ trường này chỉ có thể quan sát được nếu photon là hạt phi khối lượng. Trong trường hợp photon có khối lượng, số hạng khối lượng có thể ảnh hưởng đến plasma thiên hà. Trên thực tế không một hiệu ứng nào đã được quan sát và các nhà vật lý rút ra được giới hạn khối lượng trên cho photon là m < 3×10−27 eV/c2.[23] Vectơ thế thiên hà cũng có thể được khám phá một cách trực tiếp bằng cách đo mômen xoắn tác động lên một vành từ hóa.[24] Những phương pháp này đã thu được giới hạn trên là 10−18eV/c2, được cho trong Nhóm Dữ liệu Hạt (Particle Data Group).[25]
Những giới hạn rất nhỏ này được suy ra từ sự không quan sát thấy các hiệu ứng do vectơ thế từ trường thiên hà đã được chỉ ra là những mô hình phụ thuộc.[26] Nếu khối lượng của photon được tạo ra thông qua cơ chế Higgs thì giới hạn trên cho khối lượng của photon là m≲10−14 eV/c2 do định luật Coulomb phù hợp với thí nghiệm kiểm tra nó.
Lịch sử phát triển[sửa | sửa mã nguồn]

Cho đến tận thế kỷ thứ mười tám, trong hầu hết các lý thuyết, ánh sáng được hình dung như là dòng các hạt. Mặt khác các mô hình hạt ánh sáng không giải thích một cách thuyết phục những hiện tượng như khúc xạ, nhiễu xạ hay lưỡng chiết của ánh sáng, vì thế đã xuất hiện các lý thuyết sóng ánh sáng được đề xuất bởi René Descartes (1637),[27] Robert Hooke (1665),[28] và Christian Huygens (1678);[29] tuy vậy, các mô hình hạt vẫn nổi trội hơn, đa phần là do thanh thế của Isaac Newton (một trong những người ủng hộ mạnh mẽ cho thuyết hạt).[30] Đầu thế kỷ thứ mười chín, Thomas Young và August Fresnel minh chứng cho thấy ánh sáng thể hiện tính chất giao thoa và nhiễu xạ và cho đến năm 1850 mô hình sóng đã được chấp nhận rộng rãi.[31] Năm 1865, tiên đoán của Maxwell[32] rằng ánh sáng là một sóng điện từ—và được xác nhận bằng thực nghiệm vào năm 1888 bằng sự phát hiện của Heinrich Hertz về sóng radio[33]—dường như cuối cùng đã thổi bay mô hình hạt ánh sáng.
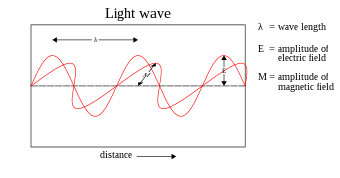
Tuy nhiên, lý thuyết sóng của Maxwell đã không miêu tả được mọi tính chất của ánh sáng. Lý thuyết Maxwell tiên đoán rằng năng lượng của sóng ánh sáng chỉ phụ thuộc vào cường độ của nó, chứ không phụ thuộc vào tần số của nó; nhưng một số thí nghiệm độc lập khác lại chỉ ra rằng năng lượng ánh sáng truyền cho các nguyên tử chỉ phụ thuộc vào tần số của nó, mà không phụ thuộc vào cường độ. Ví dụ, một số phản ứng quang hóa chỉ bỉ kích thích bởi ánh sáng với tần số cao hơn một ngưỡng xác định; nếu tần số ánh sáng thấp hơn thì sẽ không xảy ra, cho dù cường độ của tia sáng như thế nào. Tương tự, các electron có thể bật ra từ một tấm kim loại bị chiếu bởi ánh sáng có tần số đủ cao lên nó (hiệu ứng quang điện); năng lượng của electron bật ra phụ thuộc vào tần số ánh sáng, chứ không phải cường độ.[34][Ct 3]
Cũng trong thời gian này, những nghiên cứu về bức xạ vật đen đã trải qua trên bốn thập kỷ (1860–1900) bởi nhiều nhà nghiên cứu khác nhau[35] và đỉnh cao là giả thuyết của Max Planck[36][37] rằng năng lượng của bức xạ điện từ mà bất kì hệ nào hấp thụ hay phát ra bức xạ với tần số ν là một số nguyên lần của lượng tử năng lượng E=hν. Như được chỉ ra bởi Albert Einstein,[4][38] dạng lượng tử năng lượng phải được kể đến cho sự cân bằng nhiệt động quan sát thấy giữa vật chất và bức xạ điện từ; và để ghi nhận sự giải thích cho hiệu ứng quang điện, Einstein nhận được giải Nobel về vật lý năm 1921.[39]
Do lý thuyết Maxwell về ánh sáng cho phép mọi năng lượng có thể của bức xạ điện từ, nên ban đầu nhiều nhà vật lý cho rằng sự lượng tử hóa năng lượng là do một số giới hạn chưa được biết đến về quá trình bức xạ hay hấp thụ của vật chất. Năm 1905, Einstein lần đầu tiên đề xuất rằng năng lượng lượng tử hóa là một tính chất của chính bức xạ điện từ.[4] Mặc dù ông cũng công nhận lý thuyết của Maxwell, Einstein chỉ ra rằng nhiều thí nghiệm dị thường không thể giải thích được nếu năng lượng của sóng ánh sáng theo lý thuyết Maxwell bị định xứ thành những lượng tử dạng điểm mà di chuyển một cách độc lập với nhau, thậm chí nếu sóng lan truyền liên tục trong không gian.[4] Năm 1909[38] và 1916,[40] Einstein chỉ ra rằng, nếu định luật Planck về bức xạ vật đen là đúng, thì lượng tử năng lượng cũng phải mang động lượng với giá trị p=h/λ, khiến chúng có đầy đủ tính chất của một hạt. Động lượng của photon đã được quan sát bằng thực nghiệm[41] bởi Arthur Compton, và nhờ thí nghiệm này mà ông nhận được giải Nobel vật lý năm 1927. Do vậy một câu hỏi chủ chốt là: làm thế nào để thống nhất được thuyết sóng của Maxwell với những quan sát thực nghiệm về bản chất hạt của ánh sáng? Câu hỏi này đã đi theo suốt cuộc đời của Albert Einstein,[42] và được giải quyết trong điện động lực học lượng tử và lý thuyết sau nó, Mô hình chuẩn (xem Sự lượng tử hóa lần hai và Photon là boson gauge, bên dưới).
Những phản đối ban đầu[sửa | sửa mã nguồn]
Tiên đoán năm 1905 của Einstein đã được xác nhận bằng thực nghiệm theo một vài cách trong hai thập kỷ đầu tiên của thế kỷ hai mươi, như được miêu tả trong diễn văn giải Nobel của Robert Millikan.[43] Tuy nhiên, trước khi thí nghiệm Compton[41] chỉ ra là các photon mang động lượng tỉ lệ với số sóng (hay tần số) (năm 1922), hầu hết các nhà vật lý miễn cưỡng chấp nhận rằng bức xạ điện từ tự nó có dạng hạt (xem, ví dụ, diễn thuyết giải Nobel của Wien,[35] Planck[37] và Millikan.[43]). Thay vì thế, có một niềm tin phổ biến rằng sự lượng tử hóa năng lượng là kết quả một sự hạn chế chưa hiểu được của vật chất mà hấp thụ hay phát ra bức xạ. Những quan điểm này đã thay đổi dần theo thời gian. Sự thay đổi này có thể thấy rõ từ thí nghiệm về sự tán xạ Compton, mà ở đây kết quả thí nghiệm sẽ rất khó được giải thích nếu không coi chính ánh sáng bị lượng tử hóa.[44]
Thậm chí sau thí nghiệm của Compton, Bohr, Hendrik Kramers và John Slater đã thực hiện một cố gắng cuối cùng để ủng hộ mô hình trường điện từ liên tục của Maxwell về ánh sáng, gọi là mô hình BKS.[45] Trong mô hình này, để miêu tả được các kết quả thực nghiệm, hai giả thiết mạnh được đưa ra:
- Năng lượng và động lượng chỉ bảo toàn một cách trung bình trong tương tác giữa vật chất và tia bức xạ, và không bảo toàn trong các quá trình cơ bản như sự hấp thụ hay phát xạ. Điều này giải thích được (mà người ta tin rằng vào thời điểm đó) giữa sự thay đổi gián đoạn năng lượng của nguyên tử (sự chuyển dịch năng lượng giữa các trạng thái) với sự giải phóng năng lượng một cách liên tục trong tia bức xạ. (Bây giờ chúng ta biết rằng, sự giải phóng năng lượng thực sự là một quá trình liên tục, hệ kết hợp nguyên tử - trường tiến hóa theo thời gian tuân theo phương trình Schrödinger.)
- Tính nhân quả bị loại bỏ. Ví dụ, sự phát xạ tự phát chỉ là phát xạ kích thích bởi một trường điện từ "ảo".
Tuy nhiên, các thí nghiệm Compton tinh tế hơn chỉ ra rằng năng lượng và động lượng được bảo toàn một cách tuyệt vời trong các quá trình cơ bản; và rằng sự dao động của electron và sự sinh ra một photon mới trong tán xạ Compton tuân theo tính nhân quả trong phạm vi 10 ps. Cho nên, Bohr và các cộng sự đã phải gọi mô hình của họ là "một sự đưa tiễn trong danh dự".[42] Mặc dù vậy, sự thất bại của mô hình BKS đã thúc đẩy Werner Heisenberg đi đến phát triển cơ học ma trận.[46]
Một số nhà vật lý vẫn giữ thái độ ủng hộ[47] các mô hình bán cổ điển cho rằng bức xạ điện từ không bị lượng tử hóa, nhưng lại giữ quan điểm vật chất (trừ bức xạ điện từ) tuân theo các định luật của cơ học lượng tử. Mặc dù chứng cứ cho photon từ các thí nghiệm hóa học và vật lý đã áp đảo trong thập niên 1970, thì chứng cứ này không thể xem là chắc chắn tuyệt đối; do nó dựa trên sự tương tác của ánh sáng với vật chất, và họ tin là một lý thuyết đầy đủ và phức tạp về vật chất có thể về nguyên lý tính đến được chứng cứ này. Tuy thế, mọi lý thuyết bán cổ điển đã hoàn toàn bị bác bỏ trong các thập niên 1970 và 1980 bởi các thí nghiệm tương quan-photon (photon-correlation).[Ct 4] Từ đây, giả thuyết của Einstein rằng sự lượng tử hóa là một thuộc tính của bản thân ánh sáng đã được chứng minh.
Lưỡng tính sóng hạt và nguyên lý bất định[sửa | sửa mã nguồn]
Photon, giống như các đối tượng lượng tử, biểu hiện cả hai tính chất giống hạt và giống sóng. Bản chất lưỡng tính sóng-hạt của chúng khó có thể hình dung được. Photon biểu thị rõ ràng tính chất sóng trong các hiệu ứng như nhiễu xạ và giao thoa đối với các bước sóng đủ lớn. Ví dụ, một photon đi qua các khe trong thí nghiệm hai khe và biểu hiện trên màn chắn hiệu ứng giao thoa chỉ khi chúng ta không thực hiện một đo đạc nào liên quan đến photon khi nó đi qua hai khe. Sự giải thích hiện tượng này theo quan điểm của hạt ánh sáng gọi là phân phối xác suất nhưng lại biểu hiện theo phương trình Maxwell.[48] Tuy nhiên, các thí nghiệm cũng xác nhận rằng photon không phải là một xung ngắn của bức xạ điện từ; nó không dải rộng ra khi lan truyền, và cũng không bị chia ra khi đi đến một gương bán mạ.[49] Hơn nữa, photon dường như là một hạt điểm do nó bị hấp thụ hoặc phát xạ một cách toàn bộ bởi một hệ nhỏ tùy ý, những hệ nhỏ hơn bước sóng của nó, như hạt nhân nguyên tử (đường kính ≈10−15 m) hoặc thậm chí bởi hạt điểm như electron. Mặt khác, photon cũng không là một hạt điểm có quỹ đạo với hình dạng mang tính xác suất bởi trường điện từ, như được Einstein và những người khác nhận thức là vậy; và rằng giả thuyết cũng bác bỏ lại các thí nghiệm tương quan-photon đã trích dẫn ở trên. Theo như sự hiểu biết hiện tại của chúng ta, trường điện từ tự nó cũng sản sinh ra các photon, điều đó được suy ra từ đối xứng gauge định xứ và các định luật của lý thuyết trường lượng tử (xem các phần Lượng tử hóa lần hai và Boson gauge bên dưới).

Một trong những nền tảng của cơ học lượng tử đó là nguyên lý bất định của Heisenberg, nó không cho phép thực hiện được các đo đạc đồng thời về vị trí và động lượng của một hạt trong cùng một hướng. Nổi bật là, khi ta áp dụng nguyên lý bất định cho các hạt tích điện thì nó đòi hỏi sự lượng tử hóa của ánh sáng thành các hạt photon, và thậm chí sự phụ thuộc vào tần số của năng lượng và động lượng của photon. Một ví dụ đơn giản đó là thí nghiệm tưởng tượng của Heisenberg nhằm xác định vị trí của một electron bằng một kính hiển vi tưởng tượng.[50] Vị trí của electron có thể được xác định trong phạm vi của độ phân giải của kính hiển vi, được cho theo công thức của quang học cổ điển
Với là góc mở của kính hiển vi. Do đó, độ bất định vị trí là có thể nhận được một giá trị nhỏ bất kì bằng cách giảm bước sóng λ. Động lượng của electron cũng là bất định, do nó nhận được "cú hích" từ tia tán xạ từ nó vào kính hiển vi. Nếu ánh sáng không bị lượng tử hóa thành các photon, độ bất định có thể nhỏ tùy ý bằng cách giảm cường độ của chùm tia. Trong trường hợp này, do bước sóng và cường độ ánh sáng có thể thay đổi một cách độc lập với nhau, chúng ta có thể xác định được đồng thời vị trí và động lượng với một độ chính xác cao tùy ý, và điều này vi phạm nguyên lý bất định. Ngược lại, công thức của Einstein cho động lượng của photon hoàn toàn tuân theo nguyên lý bất định; do photon có thể bị tán xạ theo mọi hướng bên trong góc mở, nên độ bất định của động lượng photon bằng
Từ đó tích của chúng là , và đây chính là nguyên lý bất định của Heisenberg. Từ đó, toàn bộ thế giới bị lượng tử hóa; cả vật chất và các trường phải tuân theo những tập hợp các định luật cơ học lượng tử.[51]
Sự tương tự của nguyên lý bất định cho photon khi không cho phép đo đồng thời số các hạt photon (xem trạng thái Fock và Lượng tử hóa lần hai bên dưới) trong sóng điện từ và pha sóng của sóng này
Xem thêm trạng thái đồng pha và trạng thái đồng pha ép (squeezed coherent state).
Cả photon và các hạt khác như electron tạo ra các hình ảnh giao thoa tương tự nhau khi chúng đi qua các khe trong một thí nghiệm hai khe. Đối với các photon, điều này tương ứng với sự giao thoa của sóng Maxwell trong khi, đối với hạt vật chất, điều này tương ứng với sự giao thoa của sóng tuân theo phương trình Schrödinger. Mặc dù điều tương tự này có thể gợi ra rằng phương trình Maxwell là dạng đơn giản của phương trình Schrödinger cho các hạt photon, thì hầu hết các nhà vật lý lại cho rằng không phải như vậy.[52][53] Với lý do, chúng khác nhau rõ ràng về mặt toán học, phương trình Schrödinger có nghiệm là các trường phức, trong khi nghiệm của bốn phương trình cho các trường số thực. Tổng quát hơn, khái niệm chuẩn về hàm sóng xác suất Schrödinger không thể áp dụng được cho photon.[54] Do là hạt phi khối lượng, chúng không thể định xứ mà không bị phá hủy; hay về mặt kĩ thuật, các photon không thể có trạng thái riêng dương , và do vậy, nguyên lý bất định Heisenberg không áp dụng cho các photon. Một vài hàm sóng thay thế đã được đề xuất cho photon,[55][56][57][58] nhưng chúng đã không được sử dụng rộng rãi. Thay vào đó, các nhà vật lý đưa ra lý thuyết lượng tử hóa lần hai cho photon như được miêu tả bên dưới, điện động lực học lượng tử, trong đó các photon là những mode kích thích của trường điện từ bị lượng tử hóa.
Mô hình Bose–Einstein về chất khí photon[sửa | sửa mã nguồn]
Năm 1924, Satyendra Nath Bose suy ra định luật bức xạ vật đen Planck mà không sử dụng tới lý thuyết điện từ, mà bằng cách sửa đổi cách đếm các hạt của không gian pha.[59] Einstein đã chứng minh rằng sự thay đổi này là tương đương nếu giả sử rằng các photon hoàn toàn giống nhau và hàm ý một "tương tác phi cục bộ bí ẩn",[60][61] và bây giờ các nhà vật lý hiểu như là một sự đòi hỏi cho trạng thái cơ lượng tử đối xứng. Nghiên cứu này dẫn đến khái niệm trạng thái đồng pha và là cho sự phát triển của laser. Trong cùng các bài báo trên, Einstein đã mở rộng phương pháp của Bose cho các hạt vật chất (các boson) và ông đã tiên đoán rằng chúng có thể ngưng tụ lại thành một trạng thái lượng tử có mức năng lượng thấp nhất tại những nhiệt độ đủ thấp; và ngưng tụ Bose–Einstein đã được quan sát bằng thực nghiệm vào năm 1995.[62] Quan điểm hiện đại về các photon là, chúng là các hạt ảo với spin nguyên, các boson (ngược với các fermion với spin bán nguyên). Theo định lý spin-thống kê, mọi boson đều tuân theo thống kê Bose–Einstein (trong khi mọi fermion tuân theo thống kê Fermi-Dirac).[63]
Phát xạ kích thích và tự phát[sửa | sửa mã nguồn]

Năm 1916, Einstein chứng minh rằng định luật Planck có thể thu được từ cách suy luận bán cổ điển, phương pháp thống kê cho photon và nguyên tử, trong đó hàm ý liên hệ giữa tốc độ nguyên tử phát ra và hấp thụ các photon. Điều kiện giả thiết cho ánh sáng được phát ra và bị hấp thụ bởi nguyên tử là độc lập với nhau, và do vậy cân bằng nhiệt động được bảo tồn trong mạng nguyên tử. Xét một hốc ở trạng thái cân bằng nhiệt động học và chứa đầy bức xạ điện từ và nguyên tử có thể phát ra và hấp thụ bức xạ này. Cân bằng nhiệt đòi hỏi rằng mật độ năng lượng của các photon với tần số (tỷ lệ với số mật độ), về trung bình, là hằng số theo thời gian; và do vậy tốc độ các photon với tần số xác định được "phát ra" phải bằng tốc độ chúng được "hấp thụ".[64]
Einstein bắt đầu bằng giả sử đơn giản cho liên hệ tỷ lệ đối với những tốc độ phản ứng khác nhau tham gia vào quá trình. Trong mô hình của ông, tốc độ cho một hệ hấp thụ một photon có tần số và nguyên tử chuyển từ trạng thái năng lượng thấp lên năng lượng cao hơn bằng tỷ lệ với số các nguyên tử có năng lượng và tỷ lệ với mật độ năng lượng của các photon xung quanh với tần số này,
trong là hằng số tốc độ cho quá trình hấp thụ. Đối với quá trình ngược lại, có hai khả năng xảy ra: nguyên tử phát xạ tự phát một photon, và nó trở lại trạng thái năng lượng thấp hơn sau khi tương tác với photon va chạm (hoặc bị hấp thụ) với nó. Theo cách tiếp cận của Einstein, tốc độ tương ứng cho sự phát xạ của photon với tần số và nguyên tử chuyển từ năng lượng cao về năng lượng thấp hơn là
với là hằng số tốc độ phát xạ photon tự phát, và là hằng số tốc độ cho nguyên tử phát xạ photon tương ứng với các photon xung quanh (phát xạ kích thích hay cảm ứng). Trong cân bằng nhiệt động, số nguyên tử ở trạng thái i và số nguyên tử ở trạng thái j, trên trung bình, phải không đổi; và do vậy tốc độ và phải bằng nhau. Do đó, bằng lập luận tương tự trong thống kê Boltzmann, tỉ số giữa và bằng với là sự suy biến của trạng thái i và của j, tương ứng với mức năng lượng của chúng, k là hằng số Boltzmann và T nhiệt độ của hệ. Từ đây thu được và
Các số A và B gọi là các hệ số Einstein.[65]
Einstein không thể chứng minh đầy đủ cho phương trình tốc độ phản ứng của ông, nhưng cho rằng ông có thể tìm được các hệ số , và khi các nhà vật lý đã có được "những lý thuyết cơ học và điện động lực học tuân theo các giả thuyết lượng tử".[66] Thực tế, năm 1926, Paul Dirac tìm ra cách tính hằng số tốc độ theo cách tiếp cận bán cổ điển,[67] và, năm 1927, ông đã thành công khi tính được mọi hằng số tốc độ phản ứng từ các nguyên lý cơ sở của lý thuyết lượng tử.[68][69] Công trình của Dirac là cơ sở cho điện động lực học lượng tử QED, hay lý thuyết mô tả sự lượng tử hóa trường điện từ. Cách tiếp cận của Dirac được gọi là lượng tử hóa lần hai hay lý thuyết trường lượng tử;[70][71][72] trong khi cơ học lượng tử những ngày đầu chỉ mô tả các hạt vật chất mà không miêu tả được trường điện từ.
Einstein vướng phải khó khăn là lý thuyết của ông dường như chưa hoàn thiện, do nó không xác định được hướng của một photon phát xạ tự phát. Bản chất xác suất của chuyển động hạt-ánh sáng do Newton lần đầu tiên đề cập đến khi ông tìm cách giải thích hiện tượng lưỡng chiết và tổng quát hơn, sự tách chùm sáng ở mặt phân cách giữa chùm tới và chùm phản xạ. Newton giả thiết rằng có những biến số ẩn trong hạt ánh sáng cho phép chúng xác định đi theo đường nào.[30] Tương tự, Einstein hy vọng vào một lý thuyết đầy đủ không cho phép có sự may rủi, và bắt đầu những phê phán[42] về cơ học lượng tử. Nhưng thật trớ trêu, khi cách giải thích theo xác suất của Max Born về hàm sóng[73][74] lại được truyền cảm hứng từ công trình của Einstein trong quá trình ông đi tìm một lý thuyết đầy đủ hơn.[75]
Lượng tử hóa lần hai[sửa | sửa mã nguồn]

Năm 1910, Peter Debye suy luận ra định luật Planck cho bức xạ vật đen từ một giả thiết tương đối đơn giản.[76] Ông đã đúng khi phân tách trường điện từ trong một hốc thành những mode Fourier, và giả sử rằng năng lượng trong một mode bất kỳ là bội nguyên lần của , với là tần số của mode điện từ. Định luật Planck cho bức xạ vật đen trở thành tổng hình học của các mode này. Tuy vậy, cách tiếp cận của Debye đã không suy luận ra được công thức đúng cho thăng giáng năng lượng của bức xạ vật đen, mà Einstein đã thu được từ năm 1909.[38]
Năm 1925, Born, Heisenberg và Jordan giải thích lại khái niệm của Debye theo một hướng chìa khóa quan trọng.[77] Như đã được chỉ ra bằng lý thuyết cổ điển, các mode Fourier của trường điện từ—tập hợp đầy đủ các sóng phẳng điện từ ký hiệu bởi vectơ sóng k và trạng thái phân cực— là tương đương với các dao động tử điều hòa đơn giản không cặp. Khi giải thích theo cơ học lượng tử, các mức năng lượng của những dao động tử bằng , với là tần số của dao động. Bước mới chìa khóa tiếp theo đó là đồng nhất một mode điện từ với năng lượng như là trạng thái của photon, mỗi hạt có năng lượng . Cách tiếp cận này đã thu được công thức đúng cho thăng giáng năng lượng.

Dirac đi đến một bước xa hơn.[68][69] Ông coi tương tác giữa hạt điện tích với trường điện từ như là một nhiễu loạn nhỏ và gây ra sự chuyển dịch trạng thái photon, làm thay đổi số photon trong các mode, trong khi vẫn giữ được định luật bảo toàn năng lượng và động lượng trên tổng thể. Dirac từ đây có thể suy ra các hệ số của Einstein và , và chứng minh rằng thống kê Bose–Einstein cho photon là hệ quả tự nhiên của sự lượng tử hóa trường điện từ (cách lý giải của Bose lại đi theo hướng ngược lại; ông chứng minh định luật Planck cho bức xạ vật đen bằng giả sử thống kê B–E). Trong thời gian này, các nhà vật lý vẫn chưa biết rằng mọi boson, bao gồm photon, phải tuân theo thống kê Bose–Einstein.
Lý thuyết nhiễu loạn bậc hai của Dirac bao gồm cả các photon ảo, trạng thái trung gian tạm thời của trường điện từ; tương tác điện và từ được mang bởi những photon ảo. Trong các lý thuyết trường lượng tử, biên độ xác suất của những sự kiện quan sát được tính bằng tổng trên mọi bước trung gian có thể, ngay cả khi những bước trung gian này không có ý nghĩa vật lý; do vậy, các photon ảo không bị hạn chế bởi công thức , và chúng có thể có thêm các trạng thái phân cực; phụ thuộc vào cách trộn gauge, các photon ảo có thể có ba hay bốn trạng thái phân cực, thay vì hai trạng thái cho photon thực. Mặc dù những photon tạm thời này không thể quan sát được, chúng đóng góp vào xác suất của các sự kiện đo được. Quả thực, các tính toán nhiễu loạn bậc hai hoặc bậc cao hơn có thể đóng góp vô hạn vào tổng biên độ xác suất. Những kết quả phi vật lý được hiệu chỉnh bằng kĩ thuật tái chuẩn hóa. Những hạt ảo khác cũng đóng góp vào tổng; ví dụ, hai photon có thể tương tác gián tiếp thông qua cặp electron-positron ảo.[78] Những tán xạ photon-photon, cũng như electron-photon, là một trong những chế độ hoạt động của máy gia tốc hạt tuyến tính, đang lên kế hoạch xây dựng International Linear Collider.[79]
Theo ký hiệu vật lý hiện đại, trạng thái lượng tử của trường điện từ được viết bởi trạng thái Fock, tích tenxơ các trạng thái cho mỗi mode điện từ
với biểu diễn trạng thái trong đó photon ở trong mode . Theo ký hiệu này, một photon mới sinh ra trong mode (ví dụ, phát ra từ sự chuyển dịch nguyên tử) được viết thành . Các ký hiệu này thể hiện các khái niệm của Born, Heisenberg và Jordan miêu tả ở trên, và không cần thêm một quá trình vật lý nào khác.
Tính chất hadron của photon[sửa | sửa mã nguồn]
Những phép đo về tương tác giữa những photon năng lượng cao với các hadron cho thấy tương tác giữa chúng có cường độ mạnh hơn suy đoán so với tương tác chỉ giữa photon và điện tích của hadron. Hơn nữa tương tác của photon với proton giống như tương tác của photon với neutron[80] mặc dù hai loại hạt này có điện tích khác nhau.
Lý thuyết "Ưu thế meson vectơ" (Vector Meson Dominance-VMD) đã được phát triển nhằm giải thích hiệu ứng này. Theo VMD, photon là trạng thái chồng chập của photon điện từ thuần túy (mà chỉ xuất hiện trong tương tác giữa các hạt điện tích) và meson vectơ.[81]
Tuy nhiên, khi thực hiện thí nghiệm ở tầm tác dụng rất ngắn, cấu trúc nội tại của photon có thể được coi là dòng các thành phần tự do giả quark và gluon theo tính chất tự do tiệm cận trong QCD và được miêu tả bằng "hàm cấu trúc photon.[82][83] Bảng so sánh dữ liệu thực nghiệm với tiên đoán lý thuyết được trình bày toàn diện trong một bài viết đánh giá gần đây.[84]
Photon là boson gauge[sửa | sửa mã nguồn]
Trường điện từ là trường chuẩn (trường gauge), hay là một trường mà có phép đối xứng gauge độc lập tại mỗi vị trí trong không thời gian.[85] Đối với trường điện từ, đối xứng gauge này là nhóm đối xứng Abelian U(1) của số phức, phản ánh tính thay đổi pha của số phức mà không làm ảnh hưởng đến biến quan sát hay hàm giá trị thực với biến số phức, như năng lượng hay Lagrangian.
Lượng tử của một trường chuẩn Abelian (trường gauge) phải không có khối lượng, hay đối xứng không bị phá vỡ; từ đây, lý thuyết tiên đoán photon là hạt không có khối lượng và không có điện tích cũng như spin nguyên. Dạng đặc biệt của tương tác điện từ khiến cho spin của photon phải là ±1; do đó tính xoắn (helicity) của nó bằng . Hai thành phần spin này tương ứng với khái niệm cổ điển về sự phân cực tròn trái và phân cực tròn phải của ánh sáng. Tuy vậy, các photon ảo trung gian của điện động lực học lượng tử còn có thêm các trạng thái phân cực phi vật lý.[85]
Trong mô hình chuẩn, photon là một trong bốn boson chuẩn (hay boson gauge) của tương tác điện yếu; ba boson khác ký hiệu là W+, W− và Z0 tham gia vào tương tác yếu. Không như photon, những boson chuẩn (gauge) này có khối lượng, như được tiên đoán bởi cơ chế Higgs thông qua phá vỡ nhóm đối xứng chuẩn SU(2). Tương tác yếu thống nhất photon với các boson gauge W và Z nhờ công trình của các nhà vật lý Sheldon Glashow, Abdus Salam và Steven Weinberg, và giải Nobel Vật lý 1979 đã trao cho họ nhờ những đóng góp này.[86][87][88] Tư tưởng thống nhất các tương tác cơ bản cũng được các nhà vật lý mở rộng trong lý thuyết thống nhất lớn; thống nhất bốn boson gauge với tám boson gluon của lý thuyết sắc động lực học lượng tử; tuy nhiên, một trong những tiên đoán chìa khóa của lý thuyết này là sự phân rã của proton vẫn chưa được quan sát bằng thực nghiệm.[89]
Đóng góp vào khối lượng của hệ[sửa | sửa mã nguồn]
Khi một hệ phát ra photon thì năng lượng của hệ sẽ giảm một lượng bằng năng lượng của photon khi đo trong hệ quy chiếu quán tính, và khối lượng của hệ giảm đi bằng , tương tự khối lượng của một hệ tăng lên khi hấp thụ một photon bằng năng lượng của photon đó. Áp dụng công thức E=mc^2, phương trình bảo toàn năng lượng trong phản ứng hạt nhân có sự tham gia của photon thường được viết dưới dạng khối lượng của các hạt nhân, và số hạng cho photon của tia gamma (và cho các dạng năng lượng khác, như năng lượng phản hồi của hạt nhân).[90]
Khái niệm này cũng được áp dụng trong tiên đoán của điện động lực học lượng tử (QED). Trong lý thuyết này, khối lượng của electron (hay lepton) được hiệu chỉnh khi thêm vào đóng góp khối lượng của các photon ảo (kỹ thuật tái chuẩn hóa). Nhờ những hiệu chỉnh này mà QED có những tiên đoán bất ngờ, như mômen lưỡng cực từ dị thường của các lepton, dịch chuyển Lamb, và cấu trúc siêu tinh tế của các cặp lepton liên kết, như muonium và positronium.[91]
Photon cũng đóng góp vào thành phần của tenxơ ứng suất-năng lượng, tenxơ này là nguồn của trường hấp dẫn được mô tả trong thuyết tương đối tổng quát. Ngược lại, photon cũng bị ảnh hưởng bởi trường hấp dẫn; quỹ đạo của nó bị lệch đi trong không thời gian cong, như hiện tượng thấu kính hấp dẫn, tần số của nó cũng bị thay đổi trong hiệu ứng dịch chuyển đỏ do hấp dẫn như được kiểm chứng trong thí nghiệm Pound-Rebka. Không những chỉ đối với photon; những hiệu ứng này cũng tác động tới sóng điện từ trong lý thuyết cổ điển.[92]
Photon trong vật chất[sửa | sửa mã nguồn]
Ánh sáng truyền trong môi trường trong suốt với vận tốc nhỏ hơn c, là tốc độ ánh sáng trong chân không. Ngoài ra, ánh sáng cũng bị tán xạ hay hấp thụ. Có những hiện tượng mà sự truyền nhiệt qua môi trường chủ yếu là bức xạ, bao gồm sự phát xạ và hấp thụ photon trong nó. Ví dụ như trong lõi của Mặt Trời. Năng lượng photon phải mất khoảng một triệu năm mới tới được bề mặt.[93] Tuy nhiên, hiện tượng này khác so với sự bức xạ tán xạ đi qua môi trường vật chất, vì nó liên quan đến cân bằng địa phương giữa bức xạ và nhiệt độ. Do vậy, thời gian ở đây là thời gian vận chuyển năng lượng, chứ không phải thời gian hành trình của chính photon. Trong không gian vũ trụ, photon chỉ mất 8,3 phút đi từ Mặt Trời đến Trái Đất. Hệ số mà tốc độ ánh sáng giảm đi khi đi trong môi trường vật chất gọi là chiết suất của vật liệu. Trong cơ học sóng cổ điển, sự chậm đi này có thể giải thích bằng sự phân cực điện của vật liệu khi ánh sáng đi vào, vật liệu phân cực phát ra ánh sáng mới, và ánh sáng mới này giao thoa với ánh sáng đi vào tạo nên sự chậm trễ ánh sáng trong vật chất. Trong mô hình hạt ánh sáng, sự chậm đi này được mô tả là do quá trình kết hợp của photon với trạng thái kích thích lượng tử của vật chất (các giả hạt như phonon và exciton) để tạo ra dạng polariton; polariton này có khối lượng hiệu dụng khác không, và do đó nó không thể chuyển động với vận tốc bằng c.
Ngoài ra, photon cũng có thể coi là luôn luôn chuyển động với tốc độ c, ngay cả trong môi trường vật chất, nhưng nó có sự dịch chuyển pha (trễ hay nhanh) phụ thuộc vào tương tác với nguyên tử: điều này làm thay đổi bước sóng và động lượng của nó, nhưng không làm thay đổi tốc độ.[94] Một sóng ánh sáng cấu tạo từ những photon này lan truyền với tốc độ nhỏ hơn tốc độ ánh sáng. Theo quan điểm này các photon là "trần trụi", và bị tán xạ và dịch chuyển pha, trong khi quan điểm ở đoạn trước coi các photon là "che kín" bởi tương tác của chúng với vật chất, và lan truyền không bị tán xạ hay dịch chuyển pha, nhưng với tốc độ nhỏ hơn.
Ánh sáng với tần số khác nhau lan truyền trong vật chất với tốc độ khác nhau; hay gọi là sự tán sắc ánh sáng. Trong một số trường hợp, hiệu ứng này làm chậm tốc độ ánh sáng trong môi trường vật liệu. Sự tương tác của photon với các giả hạt khác có thể được quan sát trực tiếp trong tán xạ Raman và tán xạ Brillouin.[95]
Hạt nhân, nguyên tử và phân tử cũng hấp thụ photon, và chuyển dịch mức năng lượng của chúng. Một ví dụ cổ điển là sự chuyển dịch phân tử của anđêhít retinal C20H28O, phân tử chịu trách nhiệm cho khả năng quan sát của mắt, do nhà hóa sinh và Nobel Y học George Wald cùng đồng nghiệp phát hiện ra năm 1958. Sự hấp thụ gây ra một đồng phân cis-trans, và khi nó kết hợp với những chuyển tiếp khác, sẽ biến đổi thành xung thần kinh. Quá trình hấp thụ photon cũng làm bẻ gãy một số liên kết hóa học, như trong hiện tượng quang ly của clo, được nghiên cứu trong lĩnh vực quang hóa.[96][97] Tương tự, tia gamma trong một số tình huống có thể làm phân ly hạt nhân nguyên tử trong quá trình gọi là quang phân rã.
Ứng dụng công nghệ[sửa | sửa mã nguồn]
Photon có nhiều ứng dụng trong công nghệ. Những ví dụ dưới đây để minh họa các ứng dụng dựa trên tính chất của photon hơn là đối với thiết bị quang học nói chung như cho thấu kính, v.v mà có thể giải thích theo lý thuyết cổ điển về ánh sáng. Laser là một ứng dụng cực kỳ quan trọng và đã được mô tả ở trên với phát xạ kích thích.
Có một vài phương pháp để xác định được từng photon độc thân. Các ống nhân quang điện hoạt động dựa trên hiệu ứng quang điện: một photon chạm vào bề mặt kim loại và một electron bị bật ra, làm khởi phát một luồng khổng lồ các electron trong ống nhân quang điện. Các chip CCD sử dụng hiệu ứng tương tự trên chất bán dẫn: một photon tới làm sinh ra điện tích trên một tụ điện vi mô và từ đó có thể ghi lại được. Các thiết bị dò khác như máy đếm Geiger sử dụng khả năng photon gây ion hóa các phân tử khí, dẫn đến hình thành dòng điện mà máy đo được.[98]
Các kĩ sư và nhà hóa học thường sử dụng công thức Planck nhằm tính toán sự thay đổi năng lượng từ sự hấp thụ một photon và tiên đoán tần số ánh sáng phát ra đối với quá trình chuyển dịch năng lượng cụ thể. Ví dụ, phổ phát xạ của đèn huỳnh quang có thể tinh chỉnh bằng sử dụng các phân tử khí có mức năng lượng điện tử khác nhau và điều chỉnh năng lượng điển hình cho electron khiến phân tử khí hấp thụ nó trong bóng đèn.[Ct 5]
Dưới một số điều kiện, phải "hai" photon mới làm xảy ra sự chuyển dịch năng lượng hơn là một photon. Đây là nguyên lý cho các kính hiển vi độ phân giải cao, bởi vì các mẫu quan sát chỉ hấp thụ năng lượng trong vùng có hai chùm sáng khác màu chồng lên nhau, đồng thời cho phép thể tích bị kích thích (vùng cần quan sát) nhỏ hơn nếu chỉ dùng một chùm sáng (kính hiển vi kích thích trạng thái bởi hai photon). Quan trọng nữa là, các photon này ít gây phá hủy mẫu vật hơn do chúng mang năng lượng thấp hơn.[99]
Trong vài trường hợp, hai quá trình chuyển dịch năng lượng cũng có thể xảy ra cho hai hệ, khi một hệ hấp thụ một photon, một hệ khác gần nó "cướp" năng lượng kích thích và tái phát ra một photon với tần số khác biệt. Đây chính là cơ chế của hiện tượng truyền năng lượng cộng hưởng huỳnh quang, một kĩ thuật sử dụng trong sinh học phân tử nhằm nghiên cứu các protein thích hợp.[100]
Một vài phần cứng phát số ngẫu nhiên đòi hỏi sự xác định được một photon độc thân. Ví dụ, mỗi bit trong dãy ngẫu nhiên được tạo ra bằng cách gửi một photon đến bộ tách chùm. Trong tình huống này, có hai kết quả khả dĩ với xác suất bằng nhau xảy ra. Kết quả thực tế được sử dụng nhằm xác định bit tiếp theo trong dãy là "0" hay "1".[101][102] Công nghệ này gọi là quang tử học.
Nghiên cứu hiện nay[sửa | sửa mã nguồn]
Một lĩnh vực nghiên cứu ứng dụng của photon là quang học lượng tử. Photon là một thành tố phù hợp cho các máy tính lượng tử hoạt động cực nhanh, và hướng nghiên cứu vướng víu lượng tử của photon là một lĩnh vực rất năng động. Các quá trình quang học phi tuyến cũng là một hướng được quan tâm nhiều, với phạm vi ứng dụng quá trình hấp thụ hai photon (two-photon absorption), tự điều pha (self-phase modulation), sự bất ổn định biến điệu (modulational instability) và bộ dao động tham số quang (optical parametric oscillator). Tuy vậy, những quá trình này nói chung không chỉ giả thiết trên photon; chúng cũng có thể được áp dụng cho các nguyên tử như là những dao động tử phi tuyến. Các tinh thể phi tuyến được sử dụng để tạo ra chùm cặp photon vướng víu. Cuối cùng, photon đóng vai trò quan trọng trong thông tin quang, đặc biệt cho mật mã lượng tử.[Ct 6]
Ghi chú[sửa | sửa mã nguồn]
- ^ Mặc dù năm 1967, bản dịch của nhà xuất bản Elsevier về bài diễn thuyết giải Nobel của Planck diễn giải từ das Lichtquant là "photon", thì trong bản dịch năm 1922 của Hans Thacher Clarke và Ludwik Silberstein Nguồn gốc và sự phát triển của lý thuyết lượng tử, The Clarendon Press, 1922 (xem ở đây) sử dụng thuật ngữ "lượng tử ánh sáng". Không có chứng cứ nào cho thấy chính Planck đã sử dụng thuật ngữ "photon" đến năm 1926 (xem trong đây Lưu trữ 2019-10-01 tại Wayback Machine).
- ^ Khối lượng của photon được tin là chính xác bằng không, dựa trên các thí nghiệm và lý thuyết được miêu tả trong bài này. Một số nguồn có đưa ra khái niệm khối lượng tương đối tính, theo đó năng lượng được tính theo đơn vị khối lượng. Đối với một photon có bước sóng λ hay năng lượng E, khối lượng sẽ bằng h/λc hay E/c2. Việc sử dụng thuật ngữ khối lượng này không còn được phổ biến trong các tài liệu khoa học nữa. Xem them thông tin: Khối lượng của photon là gì? http://math.ucr.edu/home/baez/physics/ParticleAndNuclear/photon_mass.html
- ^ Nói rằng "cho dù cường độ tia sáng như thế nào" là nói đến cường độ nhỏ hơn xấp xỉ 1013 W/cm² tại điểm lý thuyết nhiễu loạn không còn tác dụng. Ngược lại, khi chiếu với cường độ cao hơn, với ánh sáng khả kiến có cường độ xấp xỉ 1014 W/cm², mô hình sóng cổ điển miêu tả chính xác năng lượng mà electron bật ra nhận được, gọi là năng lượng trọng động (ponderomotive energy). (Xem thêm: Boreham (1996). "Photon density and the correspondence principle of electromagnetic interaction".) Lấy so sánh, ánh nắng có cường độ chỉ bằng 0.1 W/cm².
- ^ Những thí nghiệm này cho kết quả không thể giải thích được bằng các mô hình bán cổ điển về ánh sáng, do chúng chứa các phản tương quan (anticorrelations) mà là kết quả từ quá trình đo trong cơ học lượng tử. Năm 1974, Clauser đã thực hiện thí nghiệm đầu tiên như vậy, và ông thông báo thấy có sự vi phạm của bất đẳng thức Cauchy–Schwarz cổ điển. Năm 1977, Kimble và cộng sự thực hiện sự tương tự với hiệu ứng phản-cụm (anti-bunching effect) của tương tác photon với một gương bán mạ; cách tiếp cận này đã loại bỏ các sai số của nguồn và làm đơn giản hơn trong thí nghiệm phản tương quan-photon (photon-anticorrelation experiment) của Grangier và các cộng sự (1986). Công trình này đã được xem xét lại và thực hiện đơn giản hơn bởi Thorn và cộng sự (2004). (Những tham khảo này được liệt kê bên dưới phần Bổ sung tài liệu tham khảo.)
- ^ Ví dụ về một bằng sáng chế Hoa Kỳ Nr. 5212709 Lưu trữ 2016-06-03 tại Wayback Machine.
- ^ Sách viết về giới thiệu quang học lượng tử có thể xem trong Fox, M. (2006). Quantum Optics: An Introduction. Oxford University Press. ISBN 0-19-856673-5.
Tham khảo[sửa | sửa mã nguồn]
- ^ a b c Amsler, C.; và đồng nghiệp (Particle Data Group) (2008). “Review of Particle Physics: Gauge and Higgs bosons” (PDF). Physics Letters B. 667 (1): 1. Bibcode:2008PhLB..667....1A. doi:10.1016/j.physletb.2008.07.018. hdl:1854/LU-685594.
- ^ Kimble, H.J.; Dagenais, M.; Mandel, L.; Dagenais; Mandel (1977). “Photon Anti-bunching in Resonance Fluorescence”. Physical Review Letters. 39 (11): 691–695. Bibcode:1977PhRvL..39..691K. doi:10.1103/PhysRevLett.39.691.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
- ^ Grangier, P.; Roger, G.; Aspect, A.; Roger; Aspect (1986). “Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences”. Europhysics Letters. 1 (4): 173–179. Bibcode:1986EL......1..173G. doi:10.1209/0295-5075/1/4/004.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
- ^ a b c d Einstein, A. (1905). “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt” (PDF). Annalen der Physik. 17: 132–148. doi:10.1002/andp.19053220607. (tiếng Đức). Một bản dịch sang tiếng Anh có tại Wikisource.
- ^ Lewis, G.N. (1926). “The conservation of photons”. Nature. 118: 874–875. doi:10.1038/118874a0. Bản gốc lưu trữ ngày 1 tháng 10 năm 2019. Truy cập ngày 17 tháng 2 năm 2011.
- ^ Asimov, I. (1966). The Neutrino, Ghost Particle of the Atom. Garden City (NY): Doubleday. ISBN 0380004836. LCCN 66-0 – 1707.
- ^ Asimov, I. (1966). The Universe From Flat Earth To Quasar. New York (NY): Walker. ISBN 080270316X. LCCN 66-0 – 2251.
- ^ Villard, P. (1900). “Sur la réflexion et la réfraction des rayons cathodiques et des rayons déviables du radium”. Comptes Rendus des Séances de l'Académie des Sciences (Paris). 130: 1010–1012. (tiếng Pháp)
- ^ Villard, P. (1900). “Sur le rayonnement du radium”. Comptes Rendus des Séances de l'Académie des Sciences (Paris). 130: 1178–1179. (tiếng Pháp)
- ^ E. Rutherford & Andrade, E.N.C. (1914). “The Wavelength of the Soft Gamma Rays from Radium B”. Tạp chí Triết học (Philosophical Magazine). 27: 854–868.Quản lý CS1: sử dụng tham số tác giả (liên kết)
- ^ V.V. Kobychev & Popov, S.B. (2005). “Constraints on the photon charge from observations of extragalactic sources”. Astronomy Letters. 31: 147–151. doi:10.1134/1.1883345.Quản lý CS1: sử dụng tham số tác giả (liên kết)
- ^ Vai trò là boson gauge và sự phân cực của photon xem phần Role 5.1 trong Aitchison, I.J.R.; Hey, A.J.G. (1993). Gauge Theories in Particle Physics. Nhà xuất bản IOP. ISBN 0-85274-328-9.
- ^ Xem trang 31 trong C. Amsler (2008). “Review of Particle Physics”. Physics Letters. B667: 1–1340. doi:10.1016/j.physletb.2008.07.018.Quản lý CS1: sử dụng tham số tác giả (liên kết)
- ^ Xem phần 1.6 trong Alonso, M.; Finn, E.J. (1968). Fundamental University Physics Volume III: Quantum and Statistical Physics. Addison-Wesley. ISBN 0-201-00262-0.
- ^ Davison E. Soper, Electromagnetic radiation is made of photons, Institute of Theoretical Science, University of Oregon
- ^ Tính chất này đã được xác nhận bằng thực nghiệm bởi Raman và Bhagavantam năm 1931: Raman, C.V.; Bhagavantam, S. (1931). “Experimental proof of the spin of the photon” (PDF). Indian Journal of Physics. 6: 353.
- ^ Ví dụ, phần 1.3.3.2 trong Burgess, C.; Moore, G. (2007). The Standard Model. A Primer. Cambridge University Press. ISBN 0-521-86036-9.
- ^ Ví dụ, phần 9.3 trong Alonso, M.; Finn, E.J. (1968). Fundamental University Physics Volume III: Quantum and Statistical Physics. Addison-Wesley.
- ^ Vd, phụ lục XXXII trong Born, M. (1962). Atomic Physics. Blackie & Son. ISBN 0486659844.
- ^ Mermin, David (tháng 2 năm 1984). “Relativity without light”. American Journal of Physics. 52 (2): 119–124. doi:10.1119/1.13917.
- ^ Plimpton, S.; Lawton, W. (1936). “A Very Accurate Test of Coulomb's Law of Force Between Charges”. Physical Review. 50: 1066. doi:10.1103/PhysRev.50.1066.
- ^ Williams, E.; Faller, J.; Hill, H. (1971). “New Experimental Test of Coulomb's Law: A Laboratory Upper Limit on the Photon Rest Mass”. Physical Review Letters. 26: 721. doi:10.1103/PhysRevLett.26.721.
- ^ Chibisov, G V (1976). “Astrophysical upper limits on the photon rest mass”. Soviet Physics Uspekhi. 19: 624. doi:10.1070/PU1976v019n07ABEH005277.
- ^ Lakes, Roderic (1998). “Experimental Limits on the Photon Mass and Cosmic Magnetic Vector Potential”. Physical Review Letters. 80: 1826. doi:10.1103/PhysRevLett.80.1826.
- ^ Amsler, C; Doser, M; Antonelli, M; Asner, D; Babu, K; Baer, H; Band, H; Barnett, R; Bergren, E (2008). “Review of Particle Physics⁎”. Physics Letters B. 667: 1. doi:10.1016/j.physletb.2008.07.018. Summary Table
- ^ Adelberger, Eric; Dvali, Gia; Gruzinov, Andrei (2007). “Photon-Mass Bound Destroyed by Vortices”. Physical Review Letters. 98: 010402. doi:10.1103/PhysRevLett.98.010402. Pdf
- ^ Descartes, R. (1637). Discours de la méthode. Imprimerie de Ian Maire. ISBN 0268008701. (tiếng Pháp)
- ^ Hooke, R. (1667). Micrographia: or some physiological descriptions of minute bodies made by magnifying glasses with observations and inquiries thereupon... Luân Đôn (UK): Royal Society of London. ISBN 0486495647.
- ^ Huygens, C. (1678). Traité de la lumière. (tiếng Pháp). Bản dịch tiếng Anh xem tại Dự án Gutenberg
- ^ a b Newton, I. (1952) [1730]. Opticks (ấn bản 4). Dover (NY): Nhà xuất bản Dover. Book II, Part III, Propositions XII–XX, Queries 25–29. ISBN 0-486-60205-2.
- ^ Buchwald, J.Z. (1989). The Rise of the Wave Theory of Light: Optical Theory and Experiment in the Early Nineteenth Century. University of Chicago Press. ISBN 0-226-07886-8. OCLC 18069573.
- ^ Maxwell, J.C. (1865). “A Dynamical Theory of the Electromagnetic Field”. Philosophical Transactions of the Royal Society of London. 155: 459–512. doi:10.1098/rstl.1865.0008. Bài viết này bắt nguồn từ buổi thuyết trình của Maxwell ngày 8 tháng 12 năm 1864 tại Hội Hoàng gia.
- ^ Hertz, H. (1888). “Über Strahlen elektrischer Kraft”. Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin). 1888: 1297–1307. (tiếng Đức)
- ^ Sự phát quang phụ thuộc vào tần số tia sáng tr. 276f., hiệu ứng quang điện phần 1.4 trong Alonso, M.; Finn, E.J. (1968). Fundamental University Physics Volume III: Quantum and Statistical Physics. Addison-Wesley. ISBN 0-201-00262-0.
- ^ a b Wien, W. (1911). “Wilhelm Wien Nobel Lecture”.
- ^ Planck, M. (1901). “Über das Gesetz der Energieverteilung im Normalspectrum”. Annalen der Physik. 4: 553–563. doi:10.1002/andp.19013090310. (tiếng Đức) Bản dịch tiếng Anh
- ^ a b Planck, M. (1920). “Max Planck's Nobel Lecture”.
- ^ a b c Einstein, A. (1909). “Über die Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung” (PDF). Physikalische Zeitschrift. 10: 817–825. (tiếng Đức). Bản dịch tiếng Anh có tại Wikisource.
- ^ Lời giới thiệu của Svante Arrhenius cho giải Nobel Vật lý năm 1921, ngày 10 tháng 12, năm 1922.Văn bản online tại [nobelprize.org], Quỹ Nobel 2008. Truy cập ngày 2008-12-05.
- ^ Einstein, A. (1916). “Zur Quantentheorie der Strahlung”. Mitteilungen der Physikalischen Gesellschaft zu Zürich. 16: 47. Also Physikalische Zeitschrift, 18, 121–128 (1917). (tiếng Đức)
- ^ a b Compton, A. (1923). “A Quantum Theory of the Scattering of X-rays by Light Elements”. Physical Review. 21: 483–502. doi:10.1103/PhysRev.21.483.
- ^ a b c Pais, A. (1982). Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press. ISBN 0-198-53907-X. Bản gốc lưu trữ ngày 20 tháng 3 năm 2014. Truy cập ngày 16 tháng 4 năm 2014.
- ^ a b Millikan, R.A (1924). “Robert A. Millikan's Nobel Lecture”.
- ^ Hendry, J. (1980). “The development of attitudes to the wave-particle duality of light and quantum theory, 1900-1920”. Annals of Science. 37 (1): 59–79. doi:10.1080/00033798000200121.
- ^ N. Bohr; Kramers, H.A.; Slater, J.C. (1924). “The Quantum Theory of Radiation”. Philosophical Magazine. 47: 785–802.Quản lý CS1: sử dụng tham số tác giả (liên kết) Also Zeitschrift für Physik, 24, 69 (1924).
- ^ Heisenberg, W. (1933). “Heisenberg Nobel lecture”.
- ^
Mandel, L. (1976). E. Wolf (biên tập). “The case for and against semiclassical radiation theory”. Progress in Optics. North-Holland. 13: 27–69. doi:10.1016/S0079-6638(08)70018-0. Đã bỏ qua tham số không rõ
|doi_brokendate=(gợi ý|doi-broken-date=) (trợ giúp) - ^ Taylor, G.I. (1909). “Interference fringes with feeble light”. Proceedings of the Cambridge Philosophical Society. 15. tr. 114–115.
- ^ Saleh, B. E. A. and Teich, M. C. (2007). Fundamentals of Photonics. Wiley. ISBN 0471358320.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
- ^ Heisenberg, W. (1927). “Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik”. Zeitschrift für Physik. 43: 172–198. doi:10.1007/BF01397280. (tiếng Đức)
- ^ E.g., p. 10f. in Schiff, L.I. (1968). Quantum Mechanics (ấn bản 3). McGraw-Hill. ISBN 0070552878. ASIN B001B3MINM..
- ^ Kramers, H.A. (1958). Quantum Mechanics. Amsterdam: North-Holland. ISBN 0486495337. ASIN B0006AUW5C.
- ^ Bohm, D. (1989) [1954]. Quantum Theory. Dover Publications. ISBN 0-486-65969-0.
- ^ T.D. Newton & Wigner, E.P. (1949). “Localized states for elementary particles”. Reviews of Modern Physics. 21: 400–406. doi:10.1103/RevModPhys.21.400.Quản lý CS1: sử dụng tham số tác giả (liên kết)
- ^ Bialynicki-Birula, I. (1994). “On the wave function of the photon” (PDF). Acta Physica Polonica A. 86: 97–116. Bản gốc (PDF) lưu trữ ngày 29 tháng 7 năm 2020. Truy cập ngày 17 tháng 2 năm 2011.
- ^ Sipe, J.E. (1995). “Photon wave functions”. Physical Review A. 52: 1875–1883. doi:10.1103/PhysRevA.52.1875.
- ^ Bialynicki-Birula, I. (1996). “Photon wave function”. Progress in Optics. 36: 245–294. doi:10.1016/S0079-6638(08)70316-0.
- ^ M.O. Scully & Zubairy, M.S. (1997). Quantum Optics. Cambridge (UK): Cambridge University Press. ISBN 0-521-43595-1.Quản lý CS1: sử dụng tham số tác giả (liên kết)
- ^ Bose, S.N. (1924). “Plancks Gesetz und Lichtquantenhypothese”. Zeitschrift für Physik. 26: 178–181. doi:10.1007/BF01327326. (tiếng Đức)
- ^ Einstein, A. (1924). “Quantentheorie des einatomigen idealen Gases”. Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse. 1924: 261–267. (tiếng Đức)
- ^ Einstein, A. (1925). “Quantentheorie des einatomigen idealen Gases, Zweite Abhandlung”. Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse. 1925: 3–14. doi:10.1002/3527608958.ch28. (tiếng Đức)
- ^ M.H. Anderson; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. (1995). “Observation of Bose–Einstein Condensation in a Dilute Atomic Vapor” (PDF). Science. 269 (5221): 198–201. doi:10.1126/science.269.5221.198. PMID 17789847.Quản lý CS1: sử dụng tham số tác giả (liên kết)
- ^ Streater, R.F.; Wightman, A.S. (1989). PCT, Spin and Statistics, and All That. Addison-Wesley. ISBN 020109410X.
- ^ Einstein, A. (1916). “Strahlungs-emission und -absorption nach der Quantentheorie”. Verhandlungen der Deutschen Physikalischen Gesellschaft. 18: 318–323. Bibcode:1916DPhyG..18..318E. (tiếng Đức)
- ^ Phần 1.4 trong Wilson, J.; Hawkes, F.J.B. (1987). Lasers: Principles and Applications. New York: Prentice Hall. ISBN 0-13-523705-X.
- ^ P. 322 in Einstein, A. (1916). “Strahlungs-emission und -absorption nach der Quantentheorie”. Verhandlungen der Deutschen Physikalischen Gesellschaft. 18: 318–323. Bibcode:1916DPhyG..18..318E. (tiếng Đức):
Die Konstanten and würden sich direkt berechnen lassen, wenn wir im Besitz einer im Sinne der Quantenhypothese modifizierten Elektrodynamik und Mechanik wären."
- ^ Dirac, P.A.M. (1926). “On the Theory of Quantum Mechanics”. Proceedings of the Royal Society A. 112 (762): 661–677. Bibcode:1926RSPSA.112..661D. doi:10.1098/rspa.1926.0133.
- ^ a b Dirac, P.A.M. (1927). “The Quantum Theory of the Emission and Absorption of Radiation” (PDF). Proceedings of the Royal Society A. 114 (767): 243–265. Bibcode:1927RSPSA.114..243D. doi:10.1098/rspa.1927.0039. Bản gốc (PDF) lưu trữ ngày 25 tháng 4 năm 2012. Truy cập ngày 4 tháng 2 năm 2013.
- ^ a b Dirac, P.A.M.year=1927b. The Quantum Theory of Dispersion. Proceedings of the Royal Society A. 114. tr. 710–728.
- ^ W. Heisenberg & Pauli, W. (1929). “Zur Quantentheorie der Wellenfelder”. European Physical Journal-Zeitschrift für Physik. 56: 1. Bibcode:1929ZPhy...56....1H. doi:10.1007/BF01340129.Quản lý CS1: sử dụng tham số tác giả (liên kết) (tiếng Đức)
- ^ W. Heisenberg & Pauli, W. (1930). “Zur Quantentheorie der Wellenfelder”. European Physical Journal-Zeitschrift für Physik. 59 (3–4): 139. Bibcode:1930ZPhy...59..168H. doi:10.1007/BF01341423.Quản lý CS1: sử dụng tham số tác giả (liên kết) (tiếng Đức)
- ^ Fermi, E. (1932). “Quantum Theory of Radiation” (PDF). Reviews of Modern Physics. 4: 87. Bibcode:1932RvMP....4...87F. doi:10.1103/RevModPhys.4.87.[liên kết hỏng]
- ^ Born, M. (1926). “Zur Quantenmechanik der Stossvorgänge” (PDF). Zeitschrift für Physik. 37 (12): 863–867. Bibcode:1926ZPhy...37..863B. doi:10.1007/BF01397477.[liên kết hỏng] (tiếng Đức)
- ^ Born, M. (1926). “Quantenmechanik der Stossvorgänge”. Zeitschrift für Physik. 38 (11–12): 803. Bibcode:1926ZPhy...38..803B. doi:10.1007/BF01397184. (tiếng Đức)
- ^ Pais, A. (1986). Inward Bound: Of Matter and Forces in the Physical World. Oxford University Press. tr. 260. ISBN 0-19-851997-4. Đặc biệt là, Born công nhận đã lấy cảm hứng từ công trình chưa bao giờ được xuất bản của Einstein trong nỗ lực ông cố gắng phát triển một "lý thuyết trường ảo", ở đó các hạt điểm photon chuyển động tuân theo xác suất của trường ảo miêu tả bởi phương trình Maxwell.
- ^ Debye, P. (1910). “Der Wahrscheinlichkeitsbegriff in der Theorie der Strahlung”. Annalen der Physik. 33 (16): 1427–1434. Bibcode:1910AnP...338.1427D. doi:10.1002/andp.19103381617. (tiếng Đức)
- ^ M. Born & Heisenberg, W.; Jordan, P. (1925). “Quantenmechanik II”. European Physical Journal-Zeitschrift für Physik. 35 (8–9): 557–615. Bibcode:1926ZPhy...35..557B. doi:10.1007/BF01379806.Quản lý CS1: sử dụng tham số tác giả (liên kết) (tiếng Đức)
- ^ Phần tán xạ Photon-photon 7-3-1, Chương 8-2 trong Itzykson, C.; Zuber, J.-B. (1980). Quantum Field Theory. McGraw-Hill. ISBN 0-07-032071-3.
- ^ Weiglein, G. (2008). “Electroweak Physics at the ILC”. Journal of Physics: Conference Series. 110 (4): 042033. Bibcode:2008JPhCS.110d2033W. doi:10.1088/1742-6596/110/4/042033.
- ^ Bauer, T. H., Spital, R. D., Yennie, D. R. and Pipkin, F. M, The hadronic properties of the photon in high-energy interactions, Rev. Mod. Phys. 50, 261–436 (1978), tr 292–293
- ^ Theory of strong interactions, J. J. Sakurai, Ann. Phys., 11 (1960)
- ^ T.F. Walsh and P.M. Zerwas, Two-photon processes in the parton model, Physics Letters B44 (1973) 195
- ^ E.Witten, Anomalous cross-section for photon - photon scattering in gauge theories, Nuclear Physics B120 (1977) 189
- ^ R. Nisius, The photon structure from deep inelastic electron photon scattering, Physics Report 332 (2000) 165
- ^ a b Ryder, L.H. (1996). Quantum field theory (ấn bản 2). Cambridge University Press. ISBN 0-521-47814-6.
- ^ Sheldon Glashow Nobel lecture, delivered ngày 8 tháng 12 năm 1979.
- ^ Abdus Salam Nobel lecture, delivered ngày 8 tháng 12 năm 1979.
- ^ Steven Weinberg Nobel lecture, delivered ngày 8 tháng 12 năm 1979.
- ^ Ví dụ chương 14 trong Hughes, I. S. (1985). Elementary particles (ấn bản 2). Cambridge University Press. ISBN 0-521-26092-2.
- ^ Ví dụ phần 10.1 trong Dunlap, R.A. (2004). An Introduction to the Physics of Nuclei and Particles. Cengage Learning. ISBN 0-534-39294-6.
- ^ Radiative correction to electron mass section 7-1-2, anomalous magnetic moments section 7-2-1, Lamb shift section 7-3-2 and hyperfine splitting in positronium section 10-3 in Itzykson, C.; Zuber, J.-B. (1980). Quantum Field Theory. McGraw-Hill. ISBN 0-07-032071-3.
- ^ Ví dụ phần 9.1 (đóng góp vào nguồn hấp dẫn của photon) và phần 10.5 (ảnh hưởng của trường hấp dẫn lên ánh sáng) trong Stephani, H.; Stewart, J. (1990). General Relativity: An Introduction to the Theory of Gravitational Field. Cambridge University Press. tr. 86 ff, 108 ff. ISBN 0-521-37941-5.
- ^ Naeye, R. (1998). Through the Eyes of Hubble: Birth, Life and Violent Death of Stars. CRC Press. ISBN 0-7503-0484-7. OCLC 40180195.
- ^ Ch 4 trong Hecht, Eugene (2001). Optics. Addison Wesley. ISBN 978-0-8053-8566-3.
- ^ Polaritons section 10.10.1, Raman and Brillouin scattering section 10.11.3 in Patterson, J.D.; Bailey, B.C. (2007). Solid-State Physics: Introduction to the Theory. Springer. tr. 569 ff, 580 ff. ISBN 3-540-24115-9.
- ^ E.g., section 11-5 C in Pine, S.H.; Hendrickson, J.B.; Cram, D.J.; Hammond, G.S. (1980). Organic Chemistry (ấn bản 4). McGraw-Hill. ISBN 0-07-050115-7.
- ^ Nobel lecture given by G. Wald on ngày 12 tháng 12 năm 1967, online at nobelprize.org: The Molecular Basis of Visual Excitation.
- ^ Photomultiplier section 1.1.10, CCDs section 1.1.8, Geiger counters section 1.3.2.1 in Kitchin, C.R. (2008). Astrophysical Techniques. Boca Raton (FL): CRC Press. ISBN 1-4200-8243-4.
- ^ Denk, W.; Svoboda, K. (1997). “Photon upmanship: Why multiphoton imaging is more than a gimmick”. Neuron (journal). 18 (3): 351–357. doi:10.1016/S0896-6273(00)81237-4. PMID 9115730.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
- ^ Lakowicz, J.R. (2006). Principles of Fluorescence Spectroscopy. Springer. tr. 529 ff. ISBN 0-387-31278-1.
- ^ Jennewein, T.; Achleitner, U.; Weihs, G.; Weinfurter, H.; Zeilinger, A. (2000). “A fast and compact quantum random number generator”. Review of Scientific Instruments. 71 (4): 1675–1680. arXiv:quant-ph/9912118. Bibcode:2000RScI...71.1675J. doi:10.1063/1.1150518.
- ^ Stefanov, A.; Gisin, N.; Guinnard, O.; Guinnard, L.; Zbiden, H. (2000). “Optical quantum random number generator”. Journal of Modern Optics. 47 (4): 595–598. doi:10.1080/095003400147908.
Bổ sung tài liệu tham khảo[sửa | sửa mã nguồn]
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Ánh sáng. |
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Photon. |
Theo thời gian xuất bản:
- Clauser, J.F. (1974). “Experimental distinction between the quantum and classical field-theoretic predictions for the photoelectric effect”. Physical Review D. 9: 853–860. doi:10.1103/PhysRevD.9.853.
- Kimble, H.J.; Dagenais, M.; Mandel, L. (1977). “Photon Anti-bunching in Resonance Fluorescence”. Physical Review Letters. 39: 691–695. doi:10.1103/PhysRevLett.39.691.
- Grangier, P.; Roger, G.; Aspect, A. (1986). “Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences”. Europhysics Letters. 1: 173–179. doi:10.1209/0295-5075/1/4/004.
- Lamb, W.E. (1995). “Anti-photon”. Applied Physics B. 60: 77–84. doi:10.1007/BF01135846.
- Số đặc biệt của trang tin Optics and Photonics News (vol. 14, tháng 10 năm 2003 địa chỉ web bài viết Lưu trữ 2013-05-17 tại Wayback Machine
- Roychoudhuri, C.; Rajarshi, R. “The nature of light: what is a photon?”. Optics and Photonics News. 14: S1.
- Zajonc, A. “Light reconsidered”. Optics and Photonics News. 14: S2–S5.
- Loudon, R. “What is a photon?”. Optics and Photonics News. 14: S6–S11.
- Finkelstein, D. “What is a photon?”. Optics and Photonics News. 14: S12–S17.
- Muthukrishnan, A.; Scully, M.O.; Zubairy, M.S. “The concept of the photon—revisited”. Optics and Photonics News. 14: S18–S27.
- Mack, H.; Schleich, W.P. “A photon viewed from Wigner phase space”. Optics and Photonics News. 14: S28–S35.
- Glauber, R. (2005). “One Hundred Years of Light Quanta” (PDF). 2005 Physics Nobel Prize Lecture. Bản gốc (PDF) lưu trữ ngày 23 tháng 7 năm 2008. Truy cập ngày 17 tháng 2 năm 2011.
Liên quan đến giáo dục:
- Thorn, J.J.; Neel, M.S.; Donato, V.W.; Bergreen, G.S.; Davies, R.E.; Beck, M. (2004). “Observing the quantum behavior of light in an undergraduate laboratory” (PDF). American Journal of Physics. 72: 1210–1219. doi:10.1119/1.1737397.
- Bronner, P.; Silberhorn, Christine; Meyn, Jan-Peter (2009). “Interactive screen experiments with single photons” (PDF). European Journal of Physics. 30: 345–353. doi:10.1088/0143-0807/30/2/014. Bản gốc (PDF) lưu trữ ngày 9 tháng 8 năm 2017. Truy cập ngày 29 tháng 1 năm 2018.
|first2=thiếu|last2=(trợ giúp)
- Photon (subatomic particle) tại Encyclopædia Britannica (tiếng Anh)
- Photon tại Từ điển bách khoa Việt Nam

















































