Mặt bậc hai

Mặt bậc hai hay mặt cong bậc hai là mặt trong không gian afin ba chiều, quỹ tích những điểm thỏa mãn phương trình bậc hai dạng

a₁₁.x² + a₂₂.y² + a₃₃.z² + a₁₂.xy + a₁₃.xz + a₂₃.yz + a₁₄.x + a₂₄.y + a₃₄.z + a₄₄ = 0

Các loại mặt bậc hai cơ bản

Mặt trụ
Mặt trụ elliptic thực	${x^2 \over a^2} + {y^2 \over b^2} = 1 \,$
Mặt trụ elliptic ảo
Mặt trụ tròn xoay	${x^2 \over a^2} + {y^2 \over a^2} = 1 \,$
Mặt trụ parabolic	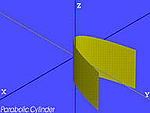$x^2 + 2ay = 0 \,$
Mặt trụ hyperbolic	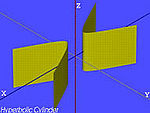${x^2 \over a^2} - {y^2 \over b^2} = 1 \,$
Mặt nón
Mặt nón elliptic thực	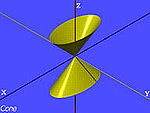${x^2 \over a^2} + {y^2 \over b^2} - {z^2 \over c^2} = 0 \,$
Mặt nón ảo${x^2 \over a^2} + {y^2 \over b^2} + {z^2 \over c^2} = 0 \,$
Mặt Ellipsoid
Mặt Ellipsoid thực	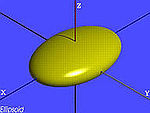${x^2 \over a^2} + {y^2 \over b^2} + {z^2 \over c^2} = 1 \,$
Mặt cầu là mặt ellipsoid với ba trục bằng nhau a = b = c
Mặt Ellipsoid ảo	${x^2 \over a^2} + {y^2 \over b^2} + {z^2 \over c^2} = -1 \,$
Mặt Hyperboloid
Mặt Hyperboloid một tầng	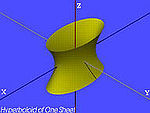${x^2 \over a^2} + {y^2 \over b^2} - {z^2 \over c^2} = 1 \,$
Mặt Hyperboloid hai tầng	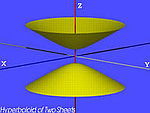${x^2 \over a^2} + {y^2 \over b^2} - {z^2 \over c^2} = - 1 \,$
Mặt hyperbolic paraboloid	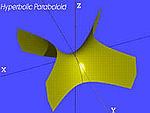${x^2 \over a^2} - {y^2 \over b^2} - z = 0 \,$
Mặt elliptic paraboloid	${x^2 \over a^2} + {y^2 \over b^2} - z = 0 \,$
Mặt elliptic paraboloid tròn xoay	${x^2 \over a^2} + {y^2 \over a^2} - z = 0 \,$
Cặp mặt phẳng thực và ảo liên hợp giao nhau
Cặp mặt phẳng thực và ảo liên hợp song song
Cặp mặt phẳng thực và ảo liên hợp trùng nhau

Tổng quát

Trong không gian xạ ảnh, mặt bậc hai là tập hợp những điểm $\{x_0, x_1, x_2, \ldots, x_n\}$ có tọa độ xạ ảnh thỏa mãn

$\sum_{i,j=0}^n a_{i,j} x_i x_j + \sum_{i=0}^n b_i x_i + R = 0$

với a_i,j không đồng thời bằng không. Với a_i,j đồng thời bằng không, ta có mặt bậc hai suy biến thành mặt phẳng trong không gian metric n chiều

Xem thêm

• Mặt phẳng
• Mặt bậc ba
• Mặt bậc bốn
• Mặt cong
• Mặt lồi
• Mặt liên tục
• Phương trình bậc hai

Liên kết ngoài

• Interactive Java 3D models of all quadric surfaces
• Mặt bậc hai trên BKTT VN
• Bài giảng về mặt bậc hai trong không gian