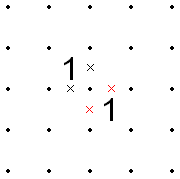Slitherlink

Slitherlink (còn được gọi là Fences, Takegaki, Loop the Loop, Loopy, Ouroboros, Suriza và Dotty Dilemma) là một trò chơi giải đố logic được phát triển bởi công ty phát hành trò chơi câu đố Nikoli, Nhật Bản, công ty Nhật đã phát triển trò chơi Sudoku.

• Câu đố Slitherlink khó vừa phải và cách giải
• 
• 

Luật chơi

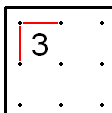
Slitherlink được chơi trên một bảng chữ nhật, được chia thành các ô vuông 1x1. Mỗi ô vuông có 1 số nguyên từ 0 đến 3, hoặc là ô trống. Nhiệm vụ của bạn là nối các điểm (là các góc của các hình vuông 1x1) thành 1 đường đi khép kín, sao cho số được ghi trên mỗi ô vuông đúng bằng số cạnh của ô vuông đó mà có đường đi đi qua. (các ô trống có thể có bao nhiêu cạnh thuộc đường đi cũng được.). Một bảng Slitherlink hợp lệ luôn có một cách giải duy nhất.

Phương pháp giải

Ký hiệu

Bất cứ khi nào số cạnh xung quanh một ô khớp với số trong ô, các cạnh tiềm năng khác phải được loại bỏ. Điều này thường được biểu thị bằng cách đánh dấu X vào các cạnh được biết là trống.

Một ký hiệu hữu ích khác khi giải Slitherlink là một cung chín mươi độ giữa hai cạnh liền kề, để chỉ ra rằng phải điền chính xác một trong hai cạnh. Một ký hiệu liên quan là một vòng cung kép giữa các cạnh liền kề, cho biết rằng phải điền cả hai hoặc cả hai. Những ký hiệu này không cần thiết cho giải pháp, nhưng có thể hữu ích trong việc tìm ra nó.

Ký hiệu vòng cung xung quanh số 2 ở một góc.

Nhiều phương pháp dưới đây có thể được chia thành hai bước đơn giản hơn bằng cách sử dụng ký hiệu vòng cung.

Chính xác 2 hoặc 0 cạnh tại mỗi điểm

Chìa khóa cho nhiều suy luận trong Slitherlink là mỗi điểm có chính xác hai cạnh kết nối với nó hoặc không có cạnh nào. Việc áp dụng quy tắc đơn giản này dẫn đến các khoản khấu trừ ngày càng phức tạp. Việc nhận ra các mẫu đơn giản này sẽ giúp ích rất nhiều trong việc giải các câu đố Slitherlink.

Góc

• 
  Nếu số 1 nằm trong một góc, thì các cạnh thực tế có thể nối được (không đánh dấu X). Lý do cạnh đánh dấu X khi nối rồi không thỏa mãn hình khép kín.
• 
  Nếu số 3 nằm trong một góc, thì hai cạnh bên ngoài của ô đó có thể được điền vào
• 
  Nếu số 2 nằm trong một góc, hai cạnh kẻ phải cách xa số 2 ở đường viền.

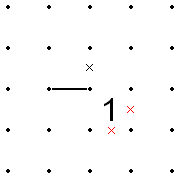
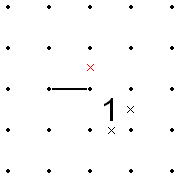
Quy tắc cho hình vuông với số 1

• 
  Nếu một đường đi vào một góc của số 1 và nếu một trong ba hướng còn lại mà đường thẳng có thể tiếp tục, hướng không phải là cạnh của hình 1 là khoảng trống đã biết, thì hai cạnh của hình 1 đối diện với góc đó có thể được loại ra (X).
• 
  Điều này cũng áp dụng ngược lại. Nghĩa là, nếu một đường thẳng đi vào góc của số 1 và hai cạnh đối diện của số 1 đã được loại ra, thì đường thẳng đó không thể rời khỏi số 1 vì điều đó sẽ đặt X xung quanh tất cả các cạnh của số 1.
• 
  Nếu hai số 1 liền kề theo đường chéo, thì trong số tám phân đoạn xung quanh hai ô đó, tập hợp "bên trong" gồm bốn phân đoạn có chung một điểm cuối (điểm được chia sẻ bởi các số 1) hoặc tập hợp bốn phân đoạn "bên ngoài" khác phải tất cả được loại bỏ ra.
• 
  Nếu hai số 1 liền kề dọc theo cạnh của lưới, thì đường giữa chúng có thể bị loại bỏ, vì sẽ không có hướng nào để nó tiếp tục khi chạm đến cạnh.

Quy tắc cho hình vuông với số 2

Nếu số 2 có bất kỳ đường X nào, thì một đường đi vào một trong hai góc không liền kề với đường ra X không thể ngay lập tức thoát ra ở các góc vuông cách xa số 2, vì khi đó hai đường xung quanh số 2 sẽ là không thể, và do đó có thể là X. Điều này có nghĩa là dòng đến phải tiếp tục ở một bên của 2 hoặc bên kia. Điều này đến lượt nó có nghĩa là dòng thứ hai của 2 phải ở phía trống duy nhất còn lại, liền kề với dòng X ban đầu, để có thể điền vào.

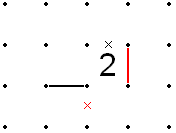
Quy tắc cho hình vuông với số 3

Nếu số 3 liền kề với số 0, theo chiều ngang hoặc chiều dọc, thì tất cả các cạnh của số 3 đó có thể được lấp đầy ngoại trừ cạnh chạm vào số 0. Ngoài ra, có thể lấp đầy hai đường vuông góc với các ô liền kề.

Nếu hai số 3 liền kề nhau theo chiều ngang hoặc chiều dọc thì cạnh chung của chúng phải được điền vào. Thứ hai, phải điền vào hai dòng bên ngoài của nhóm (song song với dòng chung).

Nếu số 3 liền kề với số 0 theo đường chéo, thì phải tô cả hai cạnh của số 3 giao với góc của số 0. Điều này là do nếu một trong hai bên đó mở, dòng kết thúc ở góc của số 0 sẽ không có chỗ để đi. Điều này tương tự như quy tắc 3 trong một góc.

Tương tự, nếu số 3 có một góc với X ở cả hai hướng đi ra khỏi góc đó, thì cả hai mặt của số 3 gặp góc đó phải được tô. Điều này là do nếu một trong hai mặt của hình 3 mở, thì mặt còn lại sẽ phải được lấp đầy (vì số 3 chỉ có thể có một mặt mở) nhưng sẽ gặp 3 chữ X ở góc đó, điều này là không thể vì mỗi điểm trên lưới phải có chính xác 2 hoặc 0 dòng.Nếu một đường kẻ đến một góc của số 3, thì phải có các đường ở cả hai bên của số 3 mà góc đó không liền kề, bởi vì nếu khoảng trống duy nhất của số 3 không liền kề với nó, thì góc sẽ có ba đường nối với nó . Hơn nữa, đoạn dẫn ra khỏi số 3 ở góc mà đường kẻ đạt tới phải trống; nếu nó được lấp đầy, cả 2 cạnh không xác định còn lại của 3 sẽ không thể chứa một dòng nào.

Quy tắc đường chéo với số 2 và số 3

Nếu hai số 3 liền nhau theo đường chéo thì phải điền các cạnh không trùng vào điểm chung.

Tương tự, nếu hai số 3 nằm trên cùng một đường chéo, nhưng cách nhau bởi bất kỳ số 2 nào (và chỉ 2) thì các cạnh bên ngoài của 3 phải được điền vào, giống như khi chúng liền kề nhau theo đường chéo.

Nếu có một chuỗi số 2 nằm trên một đường chéo và một đường góc cắt góc của số 2 ở một đầu của chuỗi, thì một đường góc phù hợp có thể được vẽ cho đến hết chuỗi.

Nếu một đường thẳng đi đến điểm bắt đầu (A) của một đường chéo chứa một hoặc nhiều số 2 và kết thúc bằng số 3, thì phải điền vào cả hai cạnh của góc xa (xa nhất từ ​​A trên đường chéo) của 3. Nếu điều này không đúng, điều đó có nghĩa là cả hai cạnh của góc gần của số 3 phải được lấp đầy, điều này có nghĩa là các góc gần của tất cả các số 2 phải được lấp đầy, bao gồm cả số 2 ở đầu đường chéo, nghĩa là không thể vì nó xung đột với đường thẳng đã đến điểm bắt đầu (A).

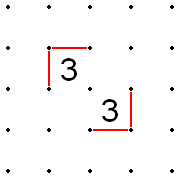
Quy tắc đường chéo với số 1 và số 3

Nếu số 1 và số 3 nằm cạnh nhau theo đường chéo và hai cạnh ngoài của số 1 bị X, thì hai cạnh ngoài của số 3 phải được điền vào.

Điều ngược lại cũng tương tự: nếu hai góc ngoài của số 3 được điền vào, thì hai góc ngoài của số 1 phải được X loại .

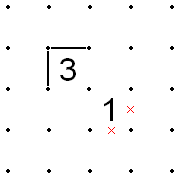
Các đường chéo bắt đầu bằng số 2

Nếu một đường thẳng đi đến một góc của hình 2 và đường thẳng phải tiếp tục đi qua một trong hai cạnh nối của hình 2, thì chính xác một trong hai cạnh còn lại của hình 2 phải được lấp đầy và đường thẳng đó phải tiếp tục đi qua một trong các cạnh đó. hai cạnh nối của hình vuông liền kề theo đường chéo.

Một quy tắc cho các khu vực khép kín

Nếu một vùng của mạng bị đóng (sao cho không có dòng nào có thể "thoát") và không trống, thì phải có một số khác không, số dòng chẵn đi vào vùng bắt đầu bên ngoài vùng. (Một số lẻ các dòng nhập có nghĩa là một số lẻ các đầu đoạn kết thúc bên trong khu vực, điều này khiến tất cả các đầu đoạn không thể kết nối. Nếu không có các dòng như vậy, các dòng bên trong khu vực không thể kết nối với các dòng bên ngoài, làm cho một giải pháp không thể.) Thông thường, quy tắc này sẽ loại bỏ một hoặc nhiều lựa chọn khả thi.Trong hình bên dưới, đường ở trên cùng bên trái sẽ đóng lại vùng trên cùng bên phải của mạng cho dù nó đi xuống hay sang phải. Đường bên phải (xung quanh hai bên của 3) đã đi vào vùng đóng. Để đáp ứng quy tắc, dòng đầu tiên phải nhập vùng và dòng thứ hai không được nhập vùng lần thứ hai. (Vì ranh giới của bất kỳ vùng đóng nào cũng đóng phần còn lại của khối hình, quy tắc cũng có thể được áp dụng cho vùng lớn hơn, phía dưới bên trái. Để áp dụng quy tắc, chỉ cần đếm các đường cắt qua ranh giới.)

Định lý đường cong Jordan

Trong một câu đố đặc biệt khó, người ta có thể sử dụng định lý đường cong Jordan, trong đó phát biểu rằng bất kỳ đường cong mở nào bắt đầu và kết thúc bên ngoài đường cong đóng phải cắt đường cong đóng một số lần Số chẵn. Đặc biệt, điều này có nghĩa là bất kỳ hàng nào của lưới phải có số chẵn các đường dọc và bất kỳ cột nào phải có số chẵn các đường ngang. Khi chỉ chưa biết một đoạn đường thế trong một trong các nhóm này, bạn có thể xác định xem nó có phải là một phần của vòng lặp hay không bằng định lý này. Điều này cũng có nghĩa là nếu bạn vạch một đường tùy ý trong đầu từ mép ngoài của lưới đến mép ngoài khác của lưới, thì đường đó sẽ cắt đường cong đã đóng một số lần chẵn.

Một chiến lược đơn giản để hỗ trợ việc sử dụng định lý này là "sơn" (đôi khi được gọi là "bóng râm") các khu vực bên ngoài và bên trong. Khi bạn nhìn thấy hai ô bên ngoài hoặc hai ô bên trong cạnh nhau, thì bạn biết rằng không có ranh giới giữa chúng. Điều ngược lại cũng đúng: nếu bạn biết không có đường kẻ giữa hai ô, thì các ô đó phải có cùng một "màu" (cả bên trong hoặc cả bên ngoài). Tương tự, nếu một ô bên ngoài và một ô bên trong liền kề nhau, bạn biết rằng phải có một đường kẻ đầy giữa chúng; và một lần nữa điều ngược lại là đúng.

Quy tắc cho câu đố chỉ có 1 giải pháp

• 
  Trong hình bên dưới, nếu một giải pháp có thể đi qua cạnh trên và bên phải của hình 2, thì phải có một giải pháp khác hoàn toàn giống như vậy ngoại trừ việc nó đi qua cạnh dưới và bên trái của hình 2, bởi vì bình phương của trên cùng và bên phải của 2 không bị giới hạn (không chứa số). Ngoài ra, giải pháp phải đi qua góc trên cùng bên phải của 2, nếu không thì phải có một giải pháp khác hoàn toàn giống nhau ngoại trừ việc nó đi qua đỉnh và cạnh bên phải của 2.
• 
  Nếu có số 2 ở một góc và hai ô vuông không thuộc đường chéo liền kề không bị giới hạn, các đường thẳng có thể được vẽ như hình bên dưới. (Trong hình, dấu chấm hỏi đại diện cho bất kỳ số nào hoặc để trống, nhưng số đó sẽ chỉ là 2 hoặc 3. Một câu đố chỉ có một giải pháp không thể có số 2 ở góc có hai ô vuông không thuộc đường chéo, không bị giới hạn và một đường chéo liền kề 0 hoặc 1.)
• 
  Nếu có hai đường đi giữa hai điểm, sao cho nghiệm chứa một điểm này cũng phải tương thích với điểm kia, thì cả hai đường đi đều có thể bị loại trừ.Trong hình bên dưới, các điểm được khoanh tròn có thể được nối với nhau bằng một đường thẳng giữa chúng và cũng có thể bằng một đường đi qua ba cạnh còn lại của hình vuông kéo dài về bên trái của các điểm. Rõ ràng (với đường màu đỏ bị bỏ qua) rằng đối với cả hai đường dẫn, phần còn lại của giải pháp có thể giống nhau – vì các ràng buộc đối với phần còn lại của giải pháp là như nhau – vì vậy cả hai đường dẫn đều bị loại trừ.

Lịch sử

Slitherlink xuất hiện lần đầu trong Puzzle Communication Nikoli số 26 (tháng 6 năm 1989). Biên tập viên đã kết hợp hai câu đố ban đầu được đóng góp ở đó. Lúc đầu, mỗi ô vuông chứa một số và các cạnh không phải tạo thành một vòng khép kín.

Trò chơi điện tử

Câu đố Slitherlink đã được giới thiệu trong trò chơi điện tử trên một số nền tảng. Một trò chơi có tên Slither Link đã được Bandai xuất bản tại Nhật Bản cho bảng điều khiển di động Wonderswan vào năm 2000. Các câu đố Slitherlink đã được đưa vào cùng với các câu đố Sudoku và Nanogram trong Tạp chí Câu đố Loppi: Loạt trò chơi Câu đố Kangaeru từ hộp mực Success for the Game Boy Nintendo Power vào năm 2001. Các trò chơi Slitherlink cũng được giới thiệu cho bảng điều khiển trò chơi cầm tay Nintendo DS, với việc Hudson Soft phát hành Puzzle Series Vol. 5: Slitherlink tại Nhật Bản vào ngày 16 tháng 11 năm 2006 và Agetec phát hành Brain Buster Puzzle Pak tại Bắc Mỹ vào ngày 17 tháng 6 năm 2007.

Liên kết ngoài

• Nikoli's English page on Slitherlink Lưu trữ 2013-05-22 tại Wayback Machine
• On the NP-completeness of the Slitherlink Puzzle Lưu trữ 2013-01-20 tại Wayback Machine - Slitherlink is NP-complete
• Site discussing non-grid forms of Slitherlink including snowflake, penrose, laves, and altair
• Slitherlink - A free site with daily slitherlink puzzles varying in difficulty. Also includes a ranking system with other players.
• Conceptis puzzles: Slitherlink techniques - This site shows some advanced solving techniques.
• games.softpedia.com - Slitherlink downloadable game. This generates puzzle at various levels and dimensions. Also you can upload a puzzle (external to the site) to solve it.
• krazydad.com - A large number of printable PDF books of slitherlink puzzles of various levels available to download or play online.
• [1] - A suggested notational system to document slitherlink puzzles.
• Loopy - One of the many simple desktop puzzle games for Windows/Unix by Simon Tatham.
• All About Slitherlink loop the loop puzzle
• Best book that explains the rules and solving techniques and history of puzzle