Hàm đặc trưng (lý thuyết xác suất)

Hàm đặc trưng của một biến ngẫu nhiên với phân phối đều U(–1,1). Hàm này là giá trị thực bởi vì nó tương ứng với một biến ngẫu nhiên đối xứng; tuy nhiên hàm đặc trưng thường có thể có giá trị phức.

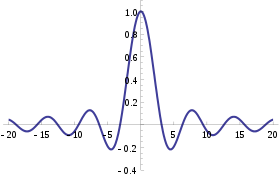
Trong lý thuyết xác suất và thống kê, hàm đặc trưng (CF) của một biến ngẫu nhiên giá trị thực là một mô tả tổng thể phân phối xác suất của nó. Nếu một biến ngẫu nhiên tồn tại hàm mật độ xác suất, thì hàm đặc trưng là biến đổi Fourier của hàm mật độ xác suất. Do đó cung cấp một cách tiếp cận khác tới kết quả phân tích dữ liệu so với làm việc trực tiếp với hàm mật độ xác suất hay hàm phân phối tích lũy. Một số kết quả đơn giản đặc biệt tồn tại cho các hàm đặc trưng của các phân phối được định nghĩa bởi tổng có trọng số của các biến ngẫu nhiên.

Ngoài các phân phối một biến, hàm đặc trưng cũng có thể được định nghĩa cho các biến ngẫu nhiên giá trị vectơ hoặc ma trận, và còn có thể được mở rộng với các trường hợp tổng quát hơn.

Hàm đặc trưng luôn tồn tại khi áp dụng với một hàm số với đối số thực, không giống như hàm sinh mô men. Có một số quan hệ giữa hành vi của hàm đặc trưng của một phân phối và các tính chất của phân phối, chẳng hạn sự tồn tại của các mô men và sự tồn tại của một hàm mật độ.

Mở đầu

Hàm đặc trưng cung cấp một tiếp cận khác để mô tả một biến ngẫu nhiên. Tương tự hàm phân phối tích lũy:

$F_{X}(x)=\operatorname {E} \left[\mathbf {1} _{\{X\leq x\}}\right]$

(trong đó 1_{{X ≤ x}} là hàm chỉ thị — nó bằng 1 khi X ≤ x, và bằng 0 nếu trái lại), hàm đặc trưng,

$\varphi _{X}(t)=\operatorname {E} \left[e^{itX}\right],$

cũng xác định hoàn toàn hành vi và tính chất của phân phối xác suất của một biến ngẫu nhiên X. Hai cách tiếp cận này là tương đưong theo cách hiểu là nếu biết một trong hai hàm thì luôn có thể tìm được hàm còn lại, nhưng chúng đưa ra những góc nhìn khác nhau để hiểu các đặc tính của biến ngẫu nhiên. Hơn nữa, trong một số trường hợp nhất định, có thể có sự khác biệt về việc liệu mỗi hàm này có thể được biểu diễn dưới dạng biểu thức với những hàm tiêu chuẩn đơn giản hay không.

Nếu hàm mật độ của một biến ngẫu nhiên được cung cấp, thì hàm đặc trưng chính là đối ngẫu Fourier của nó, nghĩa là mỗi hàm này là một biến đổi Fourier của hàm kia. Nếu một biến ngẫu nhiên có hàm sinh mô men $M_{X}(t)$, thì miền xác định của hàm đặc trưng có thể được mở rộng ra mặt phẳng phức, và ta có

$\varphi _{X}(-it)=M_{X}(t).$

Chú ý rằng hàm đặc trưng của một phân phối xác suất luôn tồn tại, ngay cả khi hàm mật độ xác suất và hàm sinh mô men không tồn tại.

Cách tiếp cận với hàm đặc trưng đặc biệt hữu ích trong phân tích các tổ hợp tuyến tính của các biến ngẫu nhiên độc lập: một chứng minh cổ điển của Định lý giới hạn trung tâm (CLT) sử dụng hàm đặc trưng và định lý liên tục Lévy. Một ứng dụng quan trong khác là trong lý thuyết về tính khai triển được của các biến ngẫu nhiên.

Định nghĩa

Đối với một biến ngẫu nhiên vô hướng X hàm đặc trưng được định nghĩa là giá trị kỳ vọng của e^itX, trong đó i là đơn vị ảo, và t ∈ R là đối số của hàm đặc trưng:

${\begin{cases}\displaystyle \varphi _{X}\!:\mathbb {R} \to \mathbb {C} \\\displaystyle \varphi _{X}(t)=\operatorname {E} \left[e^{itX}\right]=\int _{\mathbb {R} }e^{itx}\,dF_{X}(x)=\int _{\mathbb {R} }e^{itx}f_{X}(x)\,dx=\int _{0}^{1}e^{itQ_{X}(p)}\,dp\end{cases}}$

Ở đây F_X là hàm phân phối tích lũy của X, và tích phân là loại Riemann–Stieltjes. Nếu biến ngẫu nhiên X có hàm mật độ xác suất f_X, thì hàm đặc trưng là biến đổi Fourier của nó với đổi dấu ở số mũ phức,. Q_X(p) là hàm ngược của hàm phân phối tích lũy của X hay được gọi là hàm phân vị (quantile) của X. Quy ước cho các hằng số xuất hiện trong định nghĩa này của hàm đặc trưng khác với quy ước thông thường cho biến đổi Fourier. Ví dụ, một số tác giả định nghĩa φ_X(t) = E[e^−2πitX], về bản chất tức là đổi tham số. Một ký hiệu khác có thể gặp trong các tài liệu: $\scriptstyle {\hat {p}}$ là hàm đặc trưng đối với một độ đo xác suất p, hay $\scriptstyle {\hat {f}}$ là hàm đặc trưng đối với một mật độ f.

Trường hợp tổng quát

• Nếu X là một vectơ ngẫu nhiên k-chiều, thì đối với t ∈ R^k
  $$\varphi _{X}(t)=\operatorname {E} \left[\exp(it^{T}\!X)\right],$$
  trong đó ${\textstyle t^{T}}$ là chuyển vị của vectơ  ${\textstyle t}$,
• Nếu X là một ma trận ngẫu nhiên k × p, thì đối với t ∈ R^k×p
  $$\varphi _{X}(t)=\operatorname {E} \left[\exp \left(i\operatorname {tr} (t^{T}\!X)\right)\right],$$
  trong đó ${\textstyle \operatorname {tr} (\cdot )}$ là toán tử vết.

Ví dụ

Phân phối	Hàm đặc trưng φ(t)
suy biến δa	$e^{ita}$
Bernoulli Bern(p)	$1-p+pe^{it}$
nhị thức B(n, p)	$(1-p+pe^{it})^{n}$
nhị thức âm NB(r, p)	$\left({\frac {p}{1-e^{it}+pe^{it}}}\right)^{r}$
Poisson Pois(λ)	$e^{\lambda (e^{it}-1)}$
đều liên tục U(a, b)	${\frac {e^{itb}-e^{ita}}{it(b-a)}}$
đều rời rạc DU(a, b)	${\frac {e^{ita}-e^{it(b+1)}}{(1-e^{it})(b-a+1)}}$
Laplace L(μ, b)	${\frac {e^{it\mu }}{1+b^{2}t^{2}}}$
Logistic Logistic(μ,s)	$e^{i\mu t}{\frac {\pi st}{\sinh(\pi st)}}$
chuẩn N(μ, σ2)	$e^{it\mu -{\frac {1}{2}}\sigma ^{2}t^{2}}$
chi-bình phương χ2k	$(1-2it)^{-k/2}$
chi-bình phương phi trung tâm χ'2k	$e^{\frac {i\lambda t}{1-2it}}(1-2it)^{-k/2}$
Cauchy C(μ, θ)	$e^{it\mu -\theta |t|}$
Gamma Γ(k, θ)	$(1-it\theta )^{-k}$
mũ Exp(λ)	$(1-it\lambda ^{-1})^{-1}$
hình học Gf(p) (số phép thử thành công)	${\frac {p}{1-e^{it}(1-p)}}$
hình học Gt(p) (số phép thử)	${\frac {p}{e^{-it}-(1-p)}}$
chuẩn nhiều chiều N(μ, Σ)	$e^{i{\mathbf {t} ^{\mathrm {T} }{\boldsymbol {\mu }}}-{\frac {1}{2}}\mathbf {t} ^{\mathrm {T} }{\boldsymbol {\Sigma }}\mathbf {t} }$
Cauchy nhiều chiều MultiCauchy(μ, Σ)	$e^{i\mathbf {t} ^{\mathrm {T} }{\boldsymbol {\mu }}-{\sqrt {\mathbf {t} ^{\mathrm {T} }{\boldsymbol {\Sigma }}\mathbf {t} }}}$

Tham khảo

Nguồn

• Andersen, H.H.; Højbjerre, M.; Sørensen, D.; Eriksen, P.S. (1995). Linear and graphical models for the multivariate complex normal distribution. Lecture Notes in Statistics 101. New York: Springer-Verlag. ISBN 978-0-387-94521-7.
• Billingsley, Patrick (1995). Probability and measure (ấn bản 3). John Wiley & Sons. ISBN 978-0-471-00710-4.
• Bisgaard, T. M.; Sasvári, Z. (2000). Characteristic functions and moment sequences. Nova Science.
• Bochner, Salomon (1955). Harmonic analysis and the theory of probability. University of California Press.
• Cuppens, R. (1975). Decomposition of multivariate probabilities. Academic Press. ISBN 9780121994501.
• Heathcote, C.R. (1977). “The integrated squared error estimation of parameters”. Biometrika. 64 (2): 255–264. doi:10.1093/biomet/64.2.255.
• Lukacs, E. (1970). Characteristic functions. London: Griffin.
• Kotz, Samuel; Nadarajah, Saralees (2004). Multivariate T Distributions and Their Applications. Cambridge University Press.
• Manolakis, Dimitris G.; Ingle, Vinay K.; Kogon, Stephen M. (2005). Statistical and Adaptive Signal Processing: Spectral Estimation, Signal Modeling, Adaptive Filtering, and Array Processing (bằng tiếng Anh). Artech House. ISBN 978-1-58053-610-3.
• Oberhettinger, Fritz (1973). Fourier transforms of distributions and their inverses; a collection of tables. New York: Academic Press. ISBN 9780125236508.
• Paulson, A.S.; Holcomb, E.W.; Leitch, R.A. (1975). “The estimation of the parameters of the stable laws”. Biometrika. 62 (1): 163–170. doi:10.1093/biomet/62.1.163.
• Pinsky, Mark (2002). Introduction to Fourier analysis and wavelets. Brooks/Cole. ISBN 978-0-534-37660-4.
• Sobczyk, Kazimierz (2001). Stochastic differential equations. Kluwer Academic Publishers. ISBN 978-1-4020-0345-5.
• Wendel, J.G. (1961). “The non-absolute convergence of Gil-Pelaez' inversion integral”. The Annals of Mathematical Statistics. 32 (1): 338–339. doi:10.1214/aoms/1177705164.
• Yu, J. (2004). “Empirical characteristic function estimation and its applications”. Econometrics Reviews. 23 (2): 93–1223. doi:10.1081/ETC-120039605. S2CID 9076760.
• Shephard, N. G. (1991a). “From characteristic function to distribution function: A simple framework for the theory”. Econometric Theory. 7 (4): 519–529. doi:10.1017/s0266466600004746. S2CID 14668369.
• Shephard, N. G. (1991b). “Numerical integration rules for multivariate inversions”. J. Statist. Comput. Simul. 39 (1–2): 37–46. doi:10.1080/00949659108811337.
• Ansari, Abdul Fatir; Scarlett, Jonathan; Soh, Harold (2020). “A Characteristic Function Approach to Deep Implicit Generative Modeling”. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020. tr. 7478–7487.
• Li, Shengxi; Yu, Zeyang; Xiang, Min; Mandic, Danilo (2020). “Reciprocal Adversarial Learning via Characteristic Functions”. Advances in Neural Information Processing Systems 33 (NeurIPS 2020).

Liên kết ngoài

• Hazewinkel, Michiel biên tập (2001), “Characteristic function”, Bách khoa toàn thư Toán học, Springer, ISBN 978-1-55608-010-4