Phân phối chuẩn
Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin. |
Hàm mật độ xác suất Đường màu đỏ là phân phối chuẩn tắc | |
Hàm phân phối tích lũy Màu sắc tương ứng với hình trên | |
| Tham số | cho biết vị trí (thực) bình phương tỉ lệ (thực) |
| Giá | |
| Hàm mật độ xác suất | |
| Hàm phân phối tích lũy | |
| Giá trị kỳ vọng | |
| Trung vị | |
| Yếu vị | |
| Phương sai | |
| Độ xiên | 0 |
| Độ nhọn | |
| Entropy | |
| Hàm sinh mô men | |
| Hàm đặc trưng | |
Phân phối chuẩn (Tiếng Anh: normal distribution) còn gọi là phân phối Gauss hay (Hình chuông Gauss), là một phân phối xác suất cực kì quan trọng trong nhiều lĩnh vực. Nó là họ phân phối có dạng tổng quát giống nhau, chỉ khác tham số vị trí (giá trị trung bình μ) và tỉ lệ (phương sai σ2).
Phân phối chuẩn tắc (standard normal distribution) là phân phối chuẩn với giá trị trung bình (μ) bằng 0 và độ lệch chuẩn (σ) bằng 1. Phân phối chuẩn còn được gọi là đường cong chuông (bell curve) vì đồ thị của mật độ xác suất có dạng chuông.
Lịch sử[sửa | sửa mã nguồn]
Abraham de Moivre là người đầu tiên đưa ra phân phối chuẩn trong bài báo năm 1734 (được in lại trong ấn bản lần 2 The Doctrine of Chances, 1738) khi muốn xấp xỉ một phân phối nhị thức với n lớn. Kết quả được mở rộng bởi Laplace trong cuốn sách Analytical Theory of Probabilities (1812), và bây giờ gọi là định lý Moivre-Laplace.
Laplace dùng phân phối chuẩn để phân tích sai số của các thử nghiệm. Phương pháp quan trọng bình phương tối thiểu được Legendre đưa ra năm 1805. Năm 1809, Gauss, người tuyên bố đã từng sử dụng phương pháp này từ năm 1794, đã chứng minh phương pháp này bằng cách giả thiết rằng các sai số có phân phối chuẩn.
Tên gọi "đường cong chuông" do Jouffret, người đầu tiên dùng thuật ngữ "bề mặt hình chuông" năm 1872 cho phân phối chuẩn hai chiều với các thành phần độc lập. Tên gọi "phân phối chuẩn" được tạo ra bởi Charles S. Peirce, Francis Galton và Wilhelm Lexis khoảng năm 1875.
Đặc tính của phân phối chuẩn[sửa | sửa mã nguồn]
Có nhiều cách để thể hiện các đặc tính của một phân phối xác suất. Cách dễ thấy nhất là thông qua hàm mật độ xác suất (vẽ ở hình đầu tiên), nó cho biết khả năng xảy ra của mỗi giá trị của biến ngẫu nhiên. Hàm phân phối tích lũy cũng cho cùng thông tin, nhưng hình ảnh của nó thì thông tin chứa đựng không được dễ nhận thấy cho lắm (hình đi sau). Cách tương đương khi chỉ định một phân phối chuẩn là thông qua: mômen, ước lượng, hàm đặc trưng, hàm khởi tạo mômen, và hàm khởi tạo ước lượng và định lý Maxwell. Một số rất hữu ích về mặt lý thuyết, nhưng không trực quan. Xem phân phối xác suất.
Mọi ước lượng của phân phối chuẩn đều bằng 0, ngoại trừ hai cái đầu tiên.
Hàm mật độ xác suất[sửa | sửa mã nguồn]

Hàm mật độ xác suất của phân phối chuẩn với trung bình và phương sai (hay, độ lệch chuẩn ) là một ví dụ của một hàm Gauss,
(Xem thêm hàm lũy thừa và pi.)
Nếu một biến ngẫu nhiên có phân phối này, ta ký hiệu là ~ . Nếu và , phân phối được gọi là phân phối chuẩn tắc và hàm mật độ xác suất rút gọn thành
Hình ảnh bên phải cho thấy hàm mật độ xác suất cho phân phối chuẩn với các tham số khác nhau.
Một số tính chất với phân phối chuẩn:
- Hàm mật độ là đối xứng qua giá trị trung bình (giá trị kì vọng).
- Giá trị trung bình cũng là mode và trung vị của nó.
- 68.26894921371% của diện tích dưới đường cong là nằm trong khoảng 1 lần độ lệch chuẩn tính từ trị trung bình (tức là khoảng ).
- 95.44997361036% của diện tích dưới đường cong là nằm trong khoảng 2 lần độ lệch chuẩn .
- 99.73002039367% của diện tích dưới đường cong là nằm trong khoảng 3 lần độ lệch chuẩn .
- 99.99366575163% của diện tích dưới đường cong là nằm trong khoảng 4 lần độ lệch chuẩn .
- 99.99994266969% của diện tích dưới đường cong là nằm trong khoảng 5 lần độ lệch chuẩn .
- 99.99999980268% của diện tích dưới đường cong là nằm trong khoảng 6 lần độ lệch chuẩn .
- 99.99999999974% của diện tích dưới đường cong là nằm trong khoảng 7 lần độ lệch chuẩn .
Điểm uốn của đường cong xảy ra tại độ lệch chuẩn 1 tính từ trị trung bình.
Tích phân[sửa | sửa mã nguồn]
Diện tích dưới đường cong phân phối chuẩn phải bằng 1. Tiếp theo là chứng minh:
Đặt , Thì ta có .
để áp dùng biến đổi Hệ tọa độ cực, đặt lại. Ta có với Ma trận Jacobi.
Mà Định thức Jacobi , Ta có . nên .
Vậy , ta có
Hàm phân phối tích lũy[sửa | sửa mã nguồn]

Hàm phân phối tích lũy (cdf) chính là xác suất để một biến có giá trị nhỏ hơn hay bằng , và nó được biểu diễn dưới dạng hàm mật độ sau:
Hàm cdf chuẩn tắc, qui ước viết là , chỉ là từ dạng cdf tổng quát và được tính với và ,
Hàm cdf chuẩn hóa có thể được biểu diễn dưới dạng một hàm đặc biệt gọi là hàm sai số, như sau
Hàm cdf nghịch đảo, hay hàm "quantile", có thể được biểu dưới dạng nghịch đảo của hàm sai số:
Hàm "quantile" này đôi khi còn gọi là hàm "probit". Hàm "probit" không có nguyên hàm sơ cấp. Không có ở đây không phải là không tìm thấy, mà nghĩa là người ta chứng minh rằng không tồn tại một nguyên hàm như vậy.
Đôi khi cần tính: với số chữ số thập phân nhỏ bằng phương pháp:
Ví dụ: Tính với 4 chữ số thập phân:
Ta có: . Nhớ tạm 0.5
Tiếp tục: . Nhớ tạm 0.52
Tiếp tục: . Nhớ tạm 0.524
Cuối cùng:
Kết quả:
Giá trị của hàm Φ(x) có thể xấp xỉ một cách chính xác bằng nhiều phương pháp khác nhau, như tích phân số, chuỗi Taylor, hay chuỗi tiệm cận.
Hàm khởi tạo[sửa | sửa mã nguồn]
Hàm khởi tạo Mômen[sửa | sửa mã nguồn]
Hàm khởi tạo mômen được định nghĩa là giá trị kỳ vọng của . Với phân phối chuẩn, hàm được viết thành
và có thể thấy bằng cách khai triển biểu thức trong ngoặc thành bình phương đúng.
Hàm đặc trưng[sửa | sửa mã nguồn]
Hàm đặc trưng được định nghĩa là giá trị kì vọng của , với là phần ảo đơn vị. Với phân phối chuẩn, hàm đặc trưng được viết thành
Hàm đặc trưng được tính bằng cách thay thế cho trong hàm khởi tạo mômen.
Tính chất[sửa | sửa mã nguồn]
Một số tính chất của phân phối chuẩn:
- Nếu và và là các số thực, thì (xem giá trị kì vọng và phương sai).
- Nếu và là các biến ngẫu nhiên chuẩn độc lập, thì:
- Tổng của chúng là có phân phối chuẩn với (proof).
- Hiệu của chúng là có phân phối chuẩn với .
- Cả hai và là độc lập với nhau.
- Nếu và là các biến ngẫu nhiên chuẩn độc lập, thì:
- Tích của chúng tuân theo phân phối với hàm mật độ cho bởi
- với là hàm Bessel được chỉnh sửa loại 2.
- Tỉ số giữa chúng tuân theo phân phối Cauchy với .
- Tích của chúng tuân theo phân phối với hàm mật độ cho bởi
- Nếu là các biến ngẫu nhiên chuẩn tắc độc lập, thì có phân phối chi-bình phương với n bậc tự do.
Chuẩn hóa biến ngẫu nhiên có phân phối chuẩn[sửa | sửa mã nguồn]
Một hệ quả của Tính chất 1 là ta có thể quy mọi biến ngẫu nhiên phân phối chuẩn về dạng phân phối chuẩn tắc.
Nếu ~ , thì
là một biến có phân phối chuẩn tắc: ~ . Từ đó lại dẫn đến một hệ quả quan trọng là hàm phân phối tích lũy của một phân phối chuẩn nói chung sẽ là:
Ngược lại, nếu ~ , thì
là một biến ngẫu nhiên có phân phối chuẩn với trị trung bình và phương sai .
Giá trị của phân phối chuẩn hóa đã được lập thành bảng, và các phân phối chuẩn khác đều là các dạng biến đổi đơn giản từ phân phối chuẩn hóa. Do đó, có thể tra bảng giá trị phân phối tích lũy của hàm phân phối chuẩn hóa để tính các giá trị phân phối tích lũy của phân phối chuẩn.
Mô-men[sửa | sửa mã nguồn]
Một số mô-men bậc nhỏ của phân phối chuẩn:
| Number | Raw moment | Central moment | Cumulant |
|---|---|---|---|
| 0 | 1 | 0 | |
| 1 | 0 | ||
| 2 | |||
| 3 | 0 | 0 | |
| 4 | 0 |
Mọi ước lượng của phân phối chuẩn lớn hơn bậc hai đều bằng zero.
Khởi tạo biến ngẫu nhiên có phân phối chuẩn[sửa | sửa mã nguồn]
Khi mô phỏng bằng máy tính, người ta thường khởi tạo các giá trị số có phân phối chuẩn. Có nhiều cách và cách đơn giản nhất là chuyển ngược bằng hàm phân phối tích lũy chuẩn tắc. Có nhiều phương pháp hiệu quả được dùng đến, một trong chúng là biến đổi Box-Muller.
Biến đổi Box-Muller nhận hai giá trị có phân phối đều làm đầu vào và ánh xạ chúng thành giá trị có phân phối chuẩn. Phương pháp này đòi hỏi phải khởi tạo giá trị từ phân phối đều, và có nhiều phương pháp như vậy. Xem thêm khởi tạo số ngẫu nhiên.
Biến đổi Box-Muller là dựa vào: phân phối chi-bình phương với hai bậc tự do (xem tính chất 4 ở trên) là một biến ngẫu nhiên lũy thừa có thể khởi tạo dễ dàng.
Định lý giới hạn trung tâm[sửa | sửa mã nguồn]
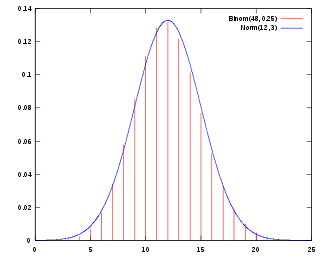
Phân phối chuẩn có một tính chất rất quan trọng là trong một số trường hợp nhất định, phân phối của tổng rất nhiều biến ngẫu nhiên độc lập sẽ có phân phối xấp xỉ chuẩn.
Đây là định lý giới hạn trung tâm.
Tầm quan trọng thực tiễn của định lý giới hạn trung tâm là phân phối chuẩn có thể được sử dụng như một xấp xỉ cho một số dạng phân phối khác.
- Một phân phối nhị thức với các tham số và được xấp xỉ chuẩn hóa đối với các giá trị lớn của và không quá gần 1 hoặc 0 (một số sách đề nghị sử dụng phép xấp xỉ này chỉ khi và đều lớn hơn hoặc bằng 5. Trong trường hợp này, cần phải hiệu chỉnh tính liên tục.
- Một phân phối Poisson với tham số được xấp xỉ chuẩn hóa đối với giá trị lớn. Phân phối chuẩn được xấp xỉ có trị trung bình và phương sai .
Việc các phép xấp xỉ trên đây có đạt được đủ độ chính xác hay không còn tùy thuộc vào mục đích sử dụng chúng và tốc độ hội tụ về phân phối chuẩn. Thường trong những trường hợp nói trên, độ kém chính xác sẽ xảy ra ở đuôi của đường phân phối.
Khả năng phân chia vô hạn[sửa | sửa mã nguồn]
Phân phối chuẩn có khả năng phân chia vô hạn.
Độ ổn định[sửa | sửa mã nguồn]
Phân phối chuẩn là phân phối xác suất ổn định.
Độ lệch chuẩn[sửa | sửa mã nguồn]

Trong thực nghiệm, ta thường giả thiết rằng dữ liệu lấy từ tổng thể có dang phân phối xấp xỉ chuẩn. Nếu giả thiết này được kiểm chứng thì có khoảng 68% số giá trị nằm trong khoảng 1 độ lệch chuẩn so với trị trung bình, khoảng 95% số giá trị trong khoảng hai lần độ lệch chuẩn và khoảng 99.7% nằm trong khoảng 3 lần độ lệch chuẩn. Đó là "quy luật 68-95-99.7" hoặc quy tắc kinh nghiệm.
Kiểm định giả thiết về phân phối chuẩn[sửa | sửa mã nguồn]
Phép kiểm định cho ta biết một bộ số liệu cho trước có dạng phân phối tương tự phân phối chuẩn hay không. Giả thiết không là số liệu giống dạng phân phối chuẩn, do đó một giá trị P đủ nhỏ sẽ chứng tỏ dữ liệu không có phân phối chuẩn.
- Phép kiểm định Kolmogorov-Smirnov
- Phép kiểm định Lilliefors
- Phép kiểm định Anderson-Darling
- Phép kiểm định Ryan-Joiner
- Phép kiểm định Sapiro-Wilk
- Đường cong phân phối chuẩn (rankit plot)
- Phép kiểm định Jarque-Bera
Các phân phối liên quan[sửa | sửa mã nguồn]
- là một phân phối Rayleigh nếu với và là 2 phân phối chuẩn độc lập.
- là một phân phối khi-bình phương với bậc tự do nếu với cho và là độc lập
- là một phân phối Cauchy nếu và và là 2 phân phối chuẩn độc lập.
- là một phân phối log-normal nếu and .
- Liên quan đến phân phối Lévy skew alpha-stable: nếu thì .
- Phân phối chuẩn rút gọn. Nếu, thì, việc rút gọn dưới tại và trên tại sẽ dẫn đến một biến ngẫu nhiên với mean , trong đó và và , trong đó là hàm mật độ xác suất của biến ngẫu nhiên chuẩn tắc.
Ước lượng tham số[sửa | sửa mã nguồn]
Ước lượng hợp lý cực đại của các tham số[sửa | sửa mã nguồn]
Giả sử
độc lập thống kê và mỗi biến đều có phân phối chuẩn với kì vọng μ và phương sai σ2. Theo ngôn ngữ thống kê, các giá trị quan trắc của các biến ngẫu nhiên này tạo thành một "mẫu từ tổng thể có phân phối chuẩn". Ta cần ước lượng "trị trung bình của tổng thể μ và độ lệch chuẩn của tổng thể σ, dựa trên các giá trị quan sát được của mẫu. Hàm mật độ xác suất liên hiệp của các biến ngẫu nhiên này là:
(Chú ý: Ở đây ký hiệu tỉ lệ có nghĩa là tỉ lệ như một hàm của và , chứ không phải tỉ lệ như một hàm của . Điểu này có thể xem như là điểm khác biệt giữa quan điểm của các nhà thống kê và nhà xác suất. Lý do về tầm quan trọng của điểm khác nhau này sẽ được đề cập dưới đây.)
Hàm hợp lý - một hàm của μ và σ là
Trong phương pháp hợp lý cực đại, các giá trị của μ và σ làm cho hàm hợp lý đạt cực đại sẽ cho ta các giá trị của ước lượng các thông số μ và σ của tổng thể.
Thông thường trong khi cực đại hóa một hàm 2 biến ta có thể xét các đạo hàm riêng. Nhưng ở đây ta sẽ khai thác một đặc điểm là giá trị của μ làm cực đại hóa hàm hợp ký với σ là cố định, không phụ thuộc vào σ. Do đó, ta có thể tìm giá trị của μ, sau đó thay thế nó vào trong phương trình hợp lý, để cuối cùng thu được giá trị của σ làm cực đại biểu thức tìm được.
Rõ ràng là hàm hợp ký là một hàm giảm của tổng
Do đó ta muốn giá trị của μ làm cực tiểu hóa tổng này. Đặt:
là "trị trung bình mẫu". Nhận thấy
Chỉ có số hạng cuối phụ thuộc vào μ và nó được cực tiểu hóa bằng
Đó là ước lượng hợp lý cực đại của μ. Khi ta thay thế giá trị này cho μ trong hàm hợp lý, ta nhận được:
Ta quy ước ký hiệu hàm "log hợp lý", nghĩa là, logarit của hàm hợp lý, bằng một chữ thường, và ta có
và sau đó
Đạo hàm này dương, bằng 0, hoặc âm tùy thuộc vào σ2 nằm giữa 0 và
hoặc bằng đại lượng đó, hoặc lớn hơn đại lượng đó.
Kết quả là trị trung bình của bình phương các sai số là một ước lượng hợp lý cực đại của σ2, và căn bậc hai của nó là ước lượng hợp lý cực đại của σ. Ước lượng này là một ước lượng chệch, nhưng có một sai số căn quân phương nhỏ hơn so với ước lượng không chệch, vốn là n/(n − 1) lần ước lượng trên.
Điều khái quát gây ngạc nhiên[sửa | sửa mã nguồn]
Đạo hàm của ước lượng hợp lý cực đại của ma trận hiệp phương sai của một phân phối đa biến chuẩn rất khó nhận ra. Nó liên quan đến định lý phổ và lý do có thể coi một đại lượng vô hướng như là vết của ma trận 1×1 hơn là chỉ một biến vô hướng. Xem thêm cách xác định các ma trận hiệp phương sai.
Ước lượng không chệch của các tham số[sửa | sửa mã nguồn]
Ước lượng hợp lý cực đại cho tổng thể đồng nghĩa với việc của một mẫu là một ước lượng không chệch của trị trung bình, và phương sai cũng vậy. Tuy nhiên điều đó chỉ có được khi trị trung bình của tổng thể đã được biết trước. Thực tế ta chỉ có một mẫu lấy từ tổng thể, và không hề có thông tin gì về trị trung bình cũng như phương sai của tổng thể. Trường hợp này ước lượng không chệch của phương sai là:
"Phương sai mẫu" này tuân theo phân phối Gamma nếu như tất cả các biến ngẫu nhiên X đều có dạng phân phối giống nhau và độc lập với nhau:
Xem thêm[sửa | sửa mã nguồn]
- Phân phối chuẩn và không tương quan không có nghĩa là độc lập thống kê (một ví dụ về hai biến ngẫu nhiên có phân phối chuẩn, không tương quan nhưng không độc lập; điều này không xảy ra trong trường hợp có phân phối chuẩn đa biến)
- Phân phối log-chuẩn
- Phân phối chuẩn đa biến
- Phân phối Gauss khái quát
- Hàm probit
- Phân phối t của Student
- Bài toán của Behrens-Fisher
Tham khảo[sửa | sửa mã nguồn]
- John Aldrich. Earliest Uses of Symbols in Probability and Statistics. Electronic document, retrieved March 20, 2005. (See "Symbols associated with the Normal Distribution".)
- Abraham de Moivre (1738). The Doctrine of Chances.
- Stephen Jay Gould (1981). The Mismeasure of Man. First edition. W. W. Norton. ISBN 0-393-01489-4.
- R. J. Herrnstein và Charles Murray (1994). The Bell Curve: Intelligence and Class Structure in American Life. Free Press. ISBN 0-02-914673-9.
- Pierre-Simon Laplace (1812). Analytical Theory of Probabilities.
- Jeff Miller, John Aldrich, et al. Earliest Known Uses of Some of the Words of Mathematics. In particular, the entries for "bell-shaped and bell curve", "normal" (distribution), "Gaussian", and "Error, law of error, theory of errors, etc.". Electronic documents, retrieved December 13, 2005.
- S. M. Stigler (1999). Statistics on the Table, chapter 22. Harvard University Press. (History of the term "normal distribution".)
- Eric W. Weisstein et al. Normal Distribution at MathWorld. Electronic document, retrieved March 20, 2005.
- Marvin Zelen and Norman C. Severo (1964). Probability Functions. Chapter 26 of Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, ed, by Milton Abramowitz và Irene A. Stegun. National Bureau of Standards.
Liên kết ngoài[sửa | sửa mã nguồn]
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Phân phối chuẩn. |
- Mô hình tương tác tính toán các phân phối (bao gồm phân phối chuẩn).
- Công cụ tính toán diện tích tự do phía dưới đưòng phân phối chuẩn Lưu trữ 2008-03-31 tại Wayback Machine từ Website Free Statistics Calculators của Daniel Soper. Tính toán diện tích lũ tích phía dưới đường cong phân phối (tức là xác suất lũy tích), cho trước z.
- Các công cụ cơ bản cho vấn đề 6-sigma
- PlanetMath: biến ngẫu nhiên phân phối chuẩn Lưu trữ 2008-05-16 tại Wayback Machine
- Thư viện khoa học GNU – Reference Manual – The Gaussian Distribution
- Công cụ tính toán phân phối – Tính xác suất và các giá trị phân giới cho phân phối chuẩn, t, khi-bình phương và phân phối F.
- Có phải phân phối chuẩn lấy theo tên Karl Gauss? Euler và họ đường cong gamma của ông; vai trò của thống kê học Lưu trữ 2006-02-10 tại Wayback Machine
- Maxwell demons: Simulating probability distributions with functions of propositional calculus Lưu trữ 2006-04-05 tại Wayback Machine
- Bảng tính phân phối chuẩn
- Máy tính trực tuyến Phân phối chuẩn
































![{\displaystyle I^{2}=\int \limits _{0}^{2\pi }\int \limits _{0}^{\infty }e^{-{\frac {r^{2}}{2}}}rdrd\theta =\int \limits _{0}^{2\pi }[-e^{-{\frac {r^{2}}{2}}}]_{0}^{\infty }d\theta =\int \limits _{0}^{2\pi }1d\theta =2\pi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fed77a81b6bbd419dd6f832e166d8379922a07c2)





![{\displaystyle \Phi (z)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {z}{\sqrt {2}}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc207a97dbcecd9eac86cabd73cf457bbade004e)










![{\displaystyle =\mathrm {E} \left[\exp(tX)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b448728641b79f79b48120c99c851ebad195da8b)





![{\displaystyle =\mathrm {E} \left[\exp(itX)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a4140011d38a1e349c13b956214f6ec71dfab88)










































































![{\displaystyle \ell ({\widehat {\mu }},\sigma )=[\mathrm {constant} ]-n\log(\sigma )-{\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2} \over 2\sigma ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e47ff783eaedfe2a139081a92ffcc6c639f1346)



