Con lắc
 |
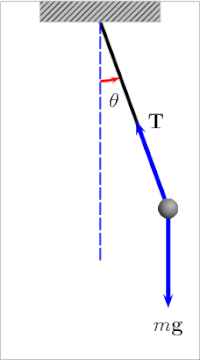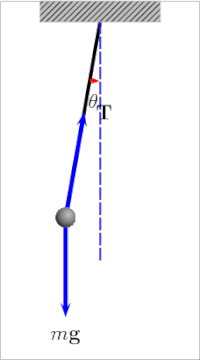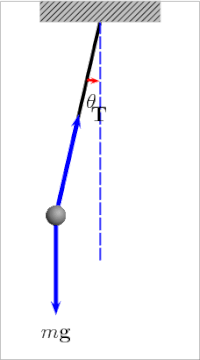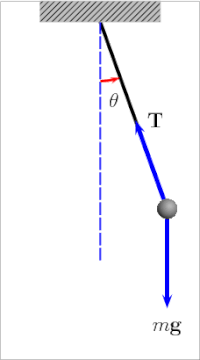
Con lắc theo định nghĩa chung nhất là một vật gắn vào một trục cố định mà nó có thể xoay (hay dao động) một cách tự do.[1] Khi đưa con lắc dịch chuyển khỏi vị trí cân bằng theo chiều ngang, nó sẽ chịu một lực phục hồi do tác dụng của hấp dẫn đưa nó trở lại vị trí cân bằng. Khi được thả ra, lực phục hồi kết hợp với trọng lượng của con lắc khiến cho nó dao động xung quanh vị trí cân bằng. Thời gian để con lắc hoàn thiện một lần dao động tới lui gọi là chu kỳ dao động. Chu kỳ dao động phụ thuộc vào độ dài của con lắc cũng như một phần vào biên độ. Tuy nhiên, nếu như biên độ là nhỏ và con lắc không chịu lực cản hay ma sát nào thì chu kỳ dao động độc lập với biên độ con lắc dao động.
Từ khi được khám phá và nghiên cứu bởi Galileo Galilei vào năm 1602, chuyển động đều của con lắc đã được ứng dụng để đo thời gian và là thiết bị đo thời gian chính xác nhất cho đến thập niên 1930.[2] Đồng hồ quả lắc được Christian Huygens phát minh vào năm 1658 đã trở thành thời gian kế tiêu chuẩn của thế giới, được sử dụng tại gia và văn phòng trong 270 năm và có sai số khoảng một giây mỗi năm trước khi nó được thay thế bởi các đồng hồ thạch anh vào những năm 1930. Con lắc cũng được áp dụng vào các dụng cụ đo đạc khoa học như gia tốc kế và địa chấn kế. Trong lịch sử, chúng còn được sử dụng trong các hấp dẫn kế để đo gia tốc hấp dẫn trong khảo sát địa lý hay thậm chí để làm đơn vị chuẩn của độ dài.[3]
Chu kỳ dao động[sửa | sửa mã nguồn]
Chu kỳ dao động của một con lắc trọng lực đơn giản phụ thuộc vào chiều dài của nó, gia tốc trọng trường địa phương và ở một mức độ nhỏ dựa trên góc cực đại mà con lắc dao động so với phương thẳng đứng, θ0, được gọi là biên độ.[4] Chu kỳ này độc lập với khối lượng của quả nặng. Nếu biên độ được giới hạn bởi dao động nhỏ[Note 1] thì chu kỳ T của một con lắc đơn (thời gian để hoàn thành một chu kỳ hoàn chỉnh) sẽ là:[5]
Trong đó là chiều dài của con lắc và là gia tốc trọng trường địa phương.
Đối với dao động nhỏ, chu kỳ dao động xấp xỉ như nhau đối với các góc khác nhau: khoảng thời gian này không phụ thuộc vào biên độ. Tính chất này, được gọi là tính đẳng thời, là lý do mà các con lắc rất hữu ích cho việc đo thời gian.[6]. Sự dao động liên tiếp của con lắc, ngay cả khi thay đổi biên độ, vẫn mất cùng một khoảng thời gian.
Đối với các biên độ lớn hơn, chu kỳ tăng dần theo biên độ nên nó sẽ dài hơn so với phương trình (1). Ví dụ, ở biên độ θ0 = 23°, chu kỳ dao động lớn hơn 1% so với phương trình (1) dự đoán. Khoảng thời gian tăng đến vô cùng khi θ0 tiến tới 180°, vì tại giá trị θ0 = 180°, hệ đang trong trạng thái cân bằng không ổn định. Chu kỳ thực sự của một con lắc trọng lực đơn giản lý tưởng có thể được viết dưới nhiều hình thức khác nhau (xem Con lắc (toán học)), một ví dụ là chuỗi vô hạn:[7][8]
đơn vị radian.
Sự khác biệt giữa khoảng thời gian thực này và khoảng thời gian cho các dao động nhỏ (1) ở trên được gọi là sai số vòng (circular error). Trong trường hợp của đồng hồ ông nội điển hình có con lắc có góc quệt là 6° và do đó biên độ là 3° (0,05 radian), chênh lệch giữa chu kỳ thực và xấp xỉ góc nhỏ (1) lên tới khoảng 15 giây mỗi ngày.
Đối với dao động nhỏ, con lắc xấp xỉ một dao động điều hòa và chuyển động của nó là một hàm của thời gian, t, là khoảng chuyển động điều hòa đơn giản:[9][10][11]
Đối với con lắc thực, thời gian thay đổi một chút theo các yếu tố như sự nổi và độ nhớt của không khí, khối lượng của dây hoặc thanh, kích thước và hình dạng của bob và cách nó được treo trên dây, và tính linh hoạt và độ căng của dây.[7][12] Trong các ứng dụng thực tế, việc hiệu chỉnh các yếu tố này có thể cần được áp dụng cho pt (1) để đưa ra con số chính xác.
Con lắc vật lý[sửa | sửa mã nguồn]
Bất kỳ hệ vật rắn nào xoay tự do quanh một trục ngang cố định được gọi là con lắc hỗn hợp hoặc con lắc vật lý. Độ dài tương đương thích hợp L để tính chu kỳ một con lắc bất kỳ như vậy chính là khoảng cách từ trục đến tâm dao động.[13] Điểm này luôn nằm dưới khối tâm; khoảng cách giữa điểm treo và tâm dao động được gọi là bán kính dao động. Vị trí của nó phụ thuộc vào phân bố khối lượng của con lắc. Nếu phần lớn khối lượng tập trung ở một quả nặng tương đối nhỏ so với chiều dài con lắc, tâm dao động sẽ gần với khối tâm.[14]
Bán kính dao động hoặc độ dài tương đương L của một con lắc vật lý bất kỳ có thể được biểu diễn như sau
trong đó là mômen quán tính của con lắc theo điểm treo, là khối lượng của con lắc và là khoảng cách giữa điểm treo và khối tâm. Thay biểu thức này vào pt (1) nêu trên, khoảng thời gian của một con lắc hỗn hợp được cho sẽ là
cho dao động đủ nhỏ.[15]
Ví dụ: một thanh đồng nhất cứng có chiều dài có mômen quán tính được cho quay quanh một đầu. Khối tâm nằm ở trung tâm của thanh, vì vậy Thay thế các giá trị này vào phương trình trên ta được . Điều này chứng tỏ rằng một con lắc vật lý có cùng chu kỳ với một con lắc đơn có chiều dài bằng 2/3 của chiều dài thanh.
Christiaan Huygens đã chứng minh vào năm 1673 rằng điểm treo và tâm dao động có thể thế chỗ nhau.[16] Điều này có nghĩa là bất kỳ con lắc nào bị đảo lộn rồi vung lên từ một trục nằm ở tâm dao động trước đó, nó sẽ có cùng chu kỳ như trước và tâm dao động mới sẽ ở điểm treo cũ. Năm 1817, Henry Kater áp dụng ý tưởng này để sản xuất một loại con lắc có thể đảo ngược, gọi là con lắc Kater, để cải thiện các phép đo gia tốc trọng trường.
Lịch sử[sửa | sửa mã nguồn]

Một trong những ứng dụng sớm nhất của con lắc là địa chấn kế vào thế kỷ I được sáng chế bởi Trương Hành, một người Trung Quốc đời nhà Hán.[17] Cơ chế hoạt động của nó là: khi có động đất, con lắc sẽ dao động và kích hoạt một trong những đòn bẩy bên trong thiết bị.[18] Đòn bẩy sẽ húc một quả bóng nhỏ rơi vào một trong tám miệng con cóc kim loại bên dưới, được đặt tại tám điểm của la bàn, biểu thị hướng của trận động đất.[18]
Nhiều nguồn[19][20][21][22] cho rằng nhà thiên văn học Ai Cập thế kỷ X Ibn Yunus đã sử dụng một con lắc để đo thời gian, nhưng đây là một sai lầm bắt nguồn từ năm 1684 bởi nhà sử học người Anh Edward Bernard.[23][24][25]
Thời Phục hưng, các con lắc bơm tay lớn được sử dụng làm nguồn năng lượng cho các máy đối ứng thủ công như cưa, ống thổi và bơm.[26] Leonardo da Vinci từng phác họa rất nhiều về chuyển động của con lắc, nhưng không nhận ra nó hữu ích trong việc đo thời gian.
1602: Nghiên cứu của Galileo[sửa | sửa mã nguồn]
Nhà khoa học người Ý Galileo Galilei là người đầu tiên nghiên cứu các tính chất của con lắc, bắt đầu vào khoảng năm 1602.[27] Báo cáo sớm nhất về nghiên cứu của ông được nhắc đến trong một bức thư gửi Guido Ubaldo dal Monte từ Padua, ngày 29 tháng 11 năm 1602.[28] Nhà viết tiểu sử và học trò của ông, Vincenzo Viviani, khẳng định rằng sự quan tâm của ông đến con lắc được khơi dậy vào khoảng năm 1582 bởi chuyển động lắc lư của một chiếc đèn chùm trong Nhà thờ Pisa.[29][30] Galileo đã khám phá ra tính chất quan trọng làm cho con lắc trở nên hữu ích trong việc đo thời gian, được gọi là tính đẳng thời; chu kì của con lắc xấp xỉ độc lập với biên độ và chiều rộng của dao động.[31] Ông cũng nhận thấy rằng khoảng thời gian này không phụ thuộc vào khối lượng của quả nặng và tỷ lệ với căn bậc hai chiều dài con lắc. Ông sử dụng các con lắc tự do trong các ứng dụng đo thời gian đơn giản. Người bạn bác sĩ của ông, Santorio Santorii, đã phát minh ra một thiết bị đo nhịp tim của bệnh nhân bằng chiều dài của một con lắc; gọi là pulsilogium.[27] Năm 1641, Galileo đã nảy ra ý tưởng và truyền ý tưởng cho con trai của mình là Vincenzo, một thiết kế đồng hồ quả lắc;[31] Vincenzo bắt đầu chế tạo thứ này, nhưng chưa kịp hoàn thành nó thì ông qua đời vào năm 1649.[32] Con lắc là cơ cấu dao động điều hòa đầu tiên được con người sử dụng.[31]
1656: Đồng hồ quả lắc[sửa | sửa mã nguồn]
Năm 1656, nhà khoa học người Hà Lan Christiaan Huygens đã chế tác chiếc đồng hồ quả lắc đầu tiên.[33] Đây là một cải tiến lớn so với đồng hồ cơ thời bấy giờ; độ lệch thời gian nhỏ nhất của chúng được cải thiện từ khoảng 15 phút mỗi ngày thành khoảng 15 giây mỗi ngày.[34] Các con lắc lan rộng khắp châu Âu khi các đồng hồ hiện có được trang bị thêm.[35]
Nhà khoa học người Anh Robert Hooke đã nghiên cứu con lắc hình nón vào khoảng năm 1666, một con lắc có thể tự do lắc theo hai chiều, với quả nặng vẽ ra quỹ đạo hình tròn hoặc hình ê-líp.[36] Ông đã sử dụng các chuyển động của thiết bị này như một mô hình để phân tích chuyển động quỹ đạo của các hành tinh.[37] Hooke đề nghị với Isaac Newton vào năm 1679 rằng các thành phần của chuyển động quỹ đạo bao gồm chuyển động quán tính dọc theo hướng tiếp tuyến cộng với chuyển động hấp dẫn theo hướng xuyên tâm. Điều này đóng góp một phần trong công thức của Newton về định luật vạn vật hấp dẫn.[38][39] Robert Hooke cũng chịu trách nhiệm đề xuất sớm nhất là vào năm 1666, rằng con lắc có thể được sử dụng để đo lực hấp dẫn.[36]
Trong chuyến thám hiểm tới Cayenne, Guiana thuộc Pháp năm 1671, Jean Richer phát hiện ra rằng đồng hồ quả lắc chạy chậm hơn 2 phút rưỡi mỗi ngày tại Cayenne so với tại Paris. Từ đó, ông suy luận rằng lực hấp dẫn ở Cayenne yếu hơn.[40][41] Vào năm 1687, Isaac Newton đã chỉ ra trong cuốn Princia Mathematica rằng, do Trái đất không phải là một hình cầu thực sự mà có phần dẹt lại (dẹt ở hai cực) do tác dụng của lực ly tâm tạo ra bởi sự tự quay của chính nó khiến lực hấp dẫn tăng theo vĩ độ.[42] Các con lắc di động tiện lợi bắt đầu được các nhà thám hiểm mang theo trong các chuyến đi đến những vùng đất xa xôi, để làm thước đo gia tốc trọng trường chính xác tại những địa điểm khác nhau trên Trái đất, cuối cùng tạo ra các mô hình chính xác về hình dạng của Trái đất.[43]
1673: Horologium Oscillatorium của Huygens[sửa | sửa mã nguồn]
Năm 1673, 17 năm sau khi phát minh ra đồng hồ quả lắc, Christiaan Huygens công bố lý thuyết về con lắc trong cuốn, Horologium Oscillatorium sive de motu Pendulorum.[44][45] Marin Mersenne và René Descartes đã phát hiện ra vào khoảng năm 1636 rằng con lắc không hoàn toàn đẳng thời; chu kỳ của nó dường như tỷ lệ thuận với biên độ.[46] Huygens phân tích vấn đề này bằng cách xác định một đường cong mà một vật phải đi theo để hạ xuống theo trọng lực đến cùng một điểm trong cùng một khoảng thời gian, bất kể điểm bắt đầu; đường cong đó chính là đường tautochrone. Bằng một phương pháp phức tạp gần giống với phép vi phân, ông đã chứng minh đường cong này là một cycloid, chứ không phải là cung tròn vệt ra bởi một con lắc,[47] xác nhận rằng con lắc không phải là đẳng thời và quan sát về đẳng tích của Galile chỉ chính xác đối với các dao động nhỏ.[48] Huygens cũng giải quyết vấn đề làm thế nào để tính chu kỳ của một con lắc có hình dạng tùy ý (gọi là con lắc vật lý), khám phá ra tâm dao động và khả năng hoán đổi của nó với điểm treo.[49]
1721: Con lắc bổ chính nhiệt độ[sửa | sửa mã nguồn]

Trong thế kỷ 18 và 19, vai trò của đồng hồ quả lắc chính xác nhất đã thúc đẩy nhiều nghiên cứu thực tế trong việc cải tiến con lắc. Người ta tìm ra một lỗi lớn, đo là dây con lắc giãn nở và co lại theo nhiệt độ môi trường, thay đổi chu kỳ xoay.[4][50] Điều này đã được giải quyết với việc phát minh ra các con lắc bổ chính nhiệt độ, con lắc thủy ngân năm 1721[51] và con lắc Gridiron năm 1726, giảm sai số trong đồng hồ quả lắc chính xác xuống vài giây mỗi tuần.[52]
Độ chính xác của các phép đo trọng lực được thực hiện với con lắc bị hạn chế bởi khó khăn trong việc tìm vị trí tâm dao động của chúng. Huygens đã phát hiện ra vào năm 1673 rằng một con lắc có cùng chu kỳ khi được treo từ tâm dao động của nó và khi được treo ở điểm trục của nó,[16] và khoảng cách giữa hai điểm bằng với chiều dài của một con lắc đơn cùng chu kỳ.[13] Năm 1818, Thuyền trưởng Henry Kater người Anh đã phát minh ra con lắc Kater có thể đảo ngược[53] sử dụng nguyên lý này, thực hiện các phép đo trọng lực rất chính xác. Trong thế kỷ tiếp theo, con lắc đảo ngược là phương pháp tiêu chuẩn để đo gia tốc trọng trường tuyệt đối.
1851: Con lắc Foucault[sửa | sửa mã nguồn]
Năm 1851, Jean Bernard Léon Foucault chỉ ra rằng mặt phẳng dao động của một con lắc, giống như con quay hồi chuyển, có xu hướng không đổi bất kể chuyển động của trục, và điều này có thể được sử dụng để chứng minh sự tự quay của Trái đất. Ông đã treo một con lắc tự do đu theo hai chiều (sau này được đặt tên là con lắc Foucault) từ mái vòm của Điện Panthéon ở Paris. Chiều dài của dây là 67 m (220 ft). Khi con lắc được cho chuyển động, mặt phẳng xoay được quan sát thấy tiến động hoặc quay 360° theo chiều kim đồng hồ trong vòng 32 giờ.[54] Đây là minh chứng đầu tiên về sự quay của Trái đất không phụ thuộc vào các quan sát thiên thể,[55] và một "cơn sốt con lắc" đã nổ ra, con lắc Foucault sau đó được trưng bày ở nhiều thành phố và thu hút đông khách tham quan.[56][57]
1930: Sụt giảm trong sử dụng[sửa | sửa mã nguồn]
Khoảng năm 1900, vật liệu giãn nở nhiệt thấp bắt đầu được sử dụng cho dây con lắc trong đồng hồ có độ chính xác cao nhất và nhiều dụng cụ khác, invar đầu tiên, một hợp kim thép niken, và sau này là thạch anh nung chảy, làm cho việc phải bổ chính nhiệt độ trở nên tào lao.[58] Các con lắc chính xác được đặt trong các bể áp suất thấp, giữ cho áp suất không khí không đổi để ngăn biến động trong chu kỳ do thay đổi độ nổi của con lắc do thay đổi áp suất khí quyển.[58] Đồng hồ quả lắc tốt nhất đạt được độ sai số khoảng một giây mỗi năm.[59][60]
Độ chính xác về thời gian của con lắc bị vượt qua bởi bộ dao động tinh thể thạch anh, được phát minh vào năm 1921 và đồng hồ thạch anh, được phát minh vào năm 1927, thay thế đồng hồ quả lắc và trở thành máy đo thời gian tốt nhất thế giới.[2] Đồng hồ quả lắc được sử dụng làm tiêu chuẩn tính giờ cho đến Thế chiến 2, mặc dù Dịch vụ thời gian của Pháp tiếp tục sử dụng chúng làm tiêu chuẩn thời gian chính thức cho đến năm 1954.[61] Trong lực kế con lắc đã được thay thế bằng các trọng lực kế "rơi tự do" vào những năm 1950,[62] nhưng các dụng cụ gồm con lắc vẫn tiếp tục được sử dụng vào những năm 1970.
Ứng dụng đo thời gian[sửa | sửa mã nguồn]
Trong 300 năm, từ khi được phát hiện ra vào khoảng năm 1582 cho đến khi đồng hồ thạch anh được phát triển vào những năm 1930, con lắc là tiêu chuẩn đo thời gian chính xác nhất.[2][63] Ngoài con lắc đồng hồ, con lắc hai giây tự do được sử dụng rộng rãi như công cụ định thời chính xác dùng trong các thí nghiệm khoa học ở thế kỷ XVII và XVIII. Con lắc đòi hỏi sự ổn định cơ học lớn: sự thay đổi chiều dài chỉ 0,02%, 0,2 mm trong con lắc đồng hồ, sẽ gây ra sai số lên đến một phút mỗi tuần.[64]
Con lắc đồng hồ[sửa | sửa mã nguồn]


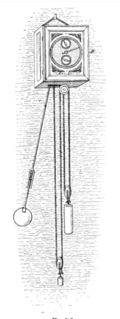
Các con lắc trong đồng hồ (xem ví dụ ở bên phải) thường là một quả nặng (b) được treo trên một thanh làm bằng gỗ hoặc kim loại (a).[4][65] Để giảm sức cản không khí (tác nhân chính làm hao tổn năng lượng trong đồng hồ chính xác)[66] quả nặng thường có hình dạng một đĩa trơn có tiết diện hình thấu kính. Trong các đồng hồ cổ hơn, quả lắc có thêm chạm khắc hoặc trang trí đặc trưng cho loại đồng hồ. Trong các đồng hồ chất lượng, quả nặng được làm nặng nhất có thể, vì điều này giúp đồng hồ cải thiện khả năng tự hiệu chỉnh của chúng. Trọng lượng phổ biến cho quả nặng con lắc hai giây là 15 pound (6,8 kg).[67] Thay vì treo trên trục, con lắc đồng hồ thường được treo trên một lò xo thẳng ngắn (d) của ruy băng kim loại linh hoạt. Cơ cấu này giảm thiểu ma sát và lực xoắn do trục quay và lực uốn nhẹ của lò xo chỉ làm tăng thêm lực phục hồi của con lắc chút ít. Đồng hồ có độ chính xác cao nhất sở hữu các lưỡi dao nằm trên các tấm làm từ đá mã não. Các xung để giữ cho con lắc dao động được cung cấp bởi một cánh tay treo sau con lắc gọi là cái nạng, (e), đầu nạng được gọi là cái nĩa, (f) có các ngạnh ôm lấy thanh lắc. Nạng đồng hồ được đẩy qua lại bởi bộ thoát đồng hồ, (g,h).
Mỗi khi con lắc dao động qua vị trí trung tâm, cơ cấu sẽ nhả ra một chiếc răng của bánh xe thoát (g). Lực của lò xo dây cót đồng hồ hoặc tải trọng con lái treo trên ròng rọc được truyền qua hệ thống bánh răng, khiến bánh xe quay và một chiếc răng ấn vào một trong những cái pallet (h), cung cấp cho con lắc một cú húc ngắn. Các bánh xe của đồng hồ, khớp với các bánh thoát, di chuyển về phía trước một lượng cố định sau mỗi vòng lắc, đẩy kim đồng hồ với tốc độ ổn định.
Con lắc phải có một cơ cấu điều chỉnh chu kỳ, thường là bằng một đai ốc điều chỉnh (c) nằm dưới quả nặng di chuyển nó lên hoặc xuống trên thanh.[4][68] Di chuyển con lắc lên làm giảm chiều dài dây, khiến cho con lắc chạy nhanh hơn và đồng hồ thêm được thời gian. Một số đồng hồ chính xác có trọng lượng điều chỉnh phụ nhỏ trên trục ren trên quả nặng, để cho phép điều chỉnh tốt hơn. Một số đồng hồ tháp và đồng hồ chính xác sử dụng một khay được gắn gần điểm giữa của thanh con lắc, giúp ta có thể thêm hoặc loại bỏ trọng lượng. Việc thêm bớt trọng lượng khiến tâm dao động bị dịch chuyển và cho phép điều chỉnh tốc độ mà không phải dừng đồng hồ.[69][70]
Con lắc phải được treo trên một giá đỡ cứng chắc.[4][71] Trong quá trình vận hành, bất kỳ độ co giãn dù có nhỏ thế nào đi chăng nữa vẫn sẽ gây ra nhiễu loạn trong chuyển động, làm xáo trộn sự đo thời gian của đồng hồ, dẫn đến các sai số. Do vậy, đồng hồ quả lắc nên được gắn chắc chắn vào một bức tường.
Chiều dài con lắc phổ biến nhất trong đồng hồ chất lượng, luôn được sử dụng trong đồng hồ ông nội, là con lắc hai giây, dài khoảng 1 mét (39 inch). Trong đồng hồ đặt kệ, con lắc nửa giây, dài 25 cm (9,8 in) hoặc ngắn hơn, được sử dụng. Chỉ có một vài đồng hồ tháp lớn sử dụng con lắc dài hơn, con lắc 1,5 giây, dài 2,25 m (7,4 ft) hoặc đôi khi là con lắc hai giây, 4 m (13 ft),[4][72] được sử dụng trên tháp đồng hồ của cung điện Westminster.[73]
Bổ chính nhiệt độ[sửa | sửa mã nguồn]

Nguồn sai số lớn nhất trong các con lắc sớm là những thay đổi nhỏ về chiều dài do sự giãn nở và sự co lại của thanh con lắc bởi sự thay đổi nhiệt độ môi trường.[74] Điều này đã được phát hiện khi có người nhận thấy đồng hồ quả lắc chạy chậm hơn khoảng một phút mỗi tuần vào mùa hè[50][75] (một trong những người đầu tiên phát hiện ra hiện tượng này là Godefroy Wendelin, được Huygens báo cáo vào năm 1658).[76] Sự giãn nở nhiệt của thanh con lắc được nghiên cứu đầu tiên bởi Jean Picard vào năm 1669.[77][78] Một con lắc có thanh thép sẽ mở rộng thêm khoảng 11,3 ppm với mỗi độ tăng Celsius, khiến nó mất khoảng 0,27 giây mỗi ngày cho mỗi độ tăng Celsius, hoặc 9 giây mỗi ngày cho sự thay đổi 33 °C (59 °F). Thanh gỗ mở rộng ít hơn, chỉ mất khoảng 6 giây mỗi ngày cho sự thay đổi 33 °C (59 °F), đó là lý do tại sao đồng hồ chất lượng thường có thanh con lắc bằng gỗ. Gỗ phải được đánh vecni để ngăn hơi nước xâm nhập, vì sự thay đổi độ ẩm cũng sẽ ảnh hưởng đến chiều dài.
Con lắc thủy ngân[sửa | sửa mã nguồn]
Thiết bị đầu tiên bù đắp cho lỗi này là con lắc thủy ngân, được phát minh bởi George Graham[51] vào năm 1721.[4][75] Thủy ngân kim loại lỏng giãn thể tích thuận với nhiệt độ. Trong một con lắc thủy ngân, quả nặng của con lắc là một vật chứa thủy ngân. Khi nhiệt độ tăng, thanh con lắc sẽ dài ra, nhưng thủy ngân cũng nở ra và mặt thoáng bề mặt của nó cũng dâng lên một chút trong vật chứa, di chuyển khối tâm của nó lại gần trục quay của con lắc. Bằng cách sử dụng một chiều cao chính xác của thủy ngân trong vật chứa, hai hiệu ứng này sẽ triệt tiêu lẫn nhau, khiến cho khối lượng của con lắc và chu kỳ của nó không thay đổi theo nhiệt độ. Nhược điểm chính của nó là khi nhiệt độ thay đổi, que sẽ nhanh chóng đạt đến nhiệt độ mới nhưng khối lượng thủy ngân có thể mất một hoặc hai ngày để đạt đến nhiệt độ mới, khiến độ chính xác bị lệch trong khoảng thời gian đó.[79] Để cải thiện sự hiệu chỉnh nhiệt, một số chỗ chứa mỏng thường được sử dụng, làm bằng kim loại. Con lắc thủy ngân là tiêu chuẩn được sử dụng trong đồng hồ bổ chính chính xác vào thế kỷ XX.[80]
Con lắc Gridiron[sửa | sửa mã nguồn]
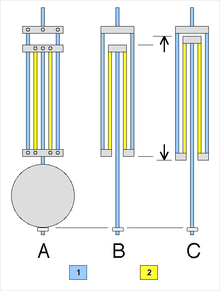
A: thiết kế mặt ngoài
B: nhiệt độ thường
C: nhiệt độ cao
Con lắc bổ chính được sử dụng rộng rãi nhất là con lắc Gridiron, được phát minh vào năm 1726 bởi John Harrison.[4][75][79] Nó bao gồm các thanh xen kẽ của hai kim loại khác nhau, một kim loại có độ giãn nở nhiệt thấp hơn (CTE), thường là thép, và một thanh có độ giãn nở nhiệt cao hơn, thường là kẽm hoặc đồng thau. Các thanh được nối với nhau bằng một khung, như được thể hiện trong hình vẽ bên phải, do đó, việc tăng chiều dài của thanh kẽm sẽ đẩy quả nặng lên, rút ngắn con lắc. Với sự gia tăng nhiệt độ, các thanh thép có độ giãn nở thấp làm cho con lắc dài hơn, trong khi các thanh kẽm có độ giãn nở cao làm cho nó ngắn hơn. Bằng cách tạo ra các thanh có độ dài chính xác, sự giãn nở lớn hơn của kẽm sẽ triệt tiêu sự giãn nở của các thanh thép có chiều dài kết hợp lớn hơn và con lắc giữ nguyên chiều dài với mọi nhiệt độ.
Con lắc gridiron thép kẽm được chế tạo bằng 5 thanh, nhưng sự giãn nở nhiệt của đồng thau gần với thép hơn, do đó, con lắc loại này thường cần 9 thanh. Các con lắc Gridiron điều chỉnh theo sự thay đổi nhiệt độ nhanh hơn các con lắc thủy ngân, nhưng các nhà khoa học phát hiện ra rằng ma sát của các thanh trượt trong các lỗ của chúng trong khung khiến cho các con lắc Gridiron phải điều chỉnh trong một loạt các cú nhảy nhỏ.[79] Trong các đồng hồ có độ chính xác cao, tốc độ của đồng hồ thay đổi đột ngột với mỗi lần nhảy. Sau này người ta phát hiện ra rằng kẽm có thể bị biến dạng dẻo nguội. Vì những lý do này, con lắc thủy ngân đã được sử dụng trong đồng hồ có độ chính xác cao nhất, còn con lắc gridiron được sử dụng trong đồng hồ hiệu chỉnh chất lượng.
Con lắc gridiron uy tín đến mức, cho đến ngày nay, nhiều con lắc đồng hồ thông thường có gridiron 'giả' trang trí mà thực sự không có chức năng bù nhiệt độ.
Thạch anh Invar và hợp nhất[sửa | sửa mã nguồn]
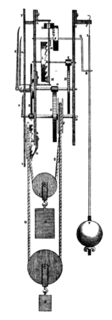
Khoảng năm 1900, các vật liệu giãn nở nhiệt thấp đã được phát triển có thể được sử dụng làm thanh lắc để tạo ra sự bù nhiệt độ phức tạp không cần thiết.[4][75] Chúng chỉ được sử dụng trong một vài đồng hồ có độ chính xác cao nhất trước khi con lắc trở nên lỗi thời như một tiêu chuẩn thời gian. Năm 1896 Charles Édouard Guillaume đã phát minh ra Invar, hợp kim thép niken. Chất này có CTE vào khoảng 0.5 µin/(in·°F), dẫn đến sai số nhiệt độ con lắc trên 71 °F chỉ là 1,3 giây mỗi ngày và lỗi dư này có thể được bù thành 0 với vài cm nhôm dưới quả nặng[2][79] (minh họa trong hình ảnh đồng hồ Riefler ở trên). Con lắc Invar được sử dụng lần đầu tiên năm 1898 trong đồng hồ hiệu chỉnh Riefler[81] đạt được độ chính xác 15 mili giây mỗi ngày. Lò xo treo của Elinvar đã được sử dụng để loại bỏ sự thay đổi nhiệt độ của lực phục hồi của lò xo trên con lắc. Thạch anh hợp nhất sau này được sử dụng có CTE thậm chí thấp hơn. Những vật liệu này là sự lựa chọn cho các con lắc có độ chính xác cao hiện đại.[82]
Áp suất khí quyển[sửa | sửa mã nguồn]
Ảnh hưởng của không khí xung quanh lên con lắc chuyển động rất phức tạp và đòi hỏi các phép tính cơ học chất lỏng với độ chính xác cao, nhưng đối với hầu hết các mục đích, ảnh hưởng của nó lên chu kỳ có thể được quy kết thành ba hiệu ứng:[58][83]
- Lực đẩy Archimedes, trọng lượng hiệu dụng của quả nặng bởi độ nổi của phần thể tích không khí mà nó thay thế, trong khi khối lượng quán tính vẫn giữ nguyên, làm giảm gia tốc của con lắc trong quá trình dao động và làm tăng chu kỳ. Điều này phụ thuộc vào áp suất không khí và mật độ của con lắc, nhưng không phụ thuộc vào hình dạng của con lắc.
- Con lắc mang một lượng không khí với nó khi nó lắc, và khối lượng của không khí này làm tăng quán tính của con lắc, làm giảm gia tốc và tăng chu kỳ. Điều này phụ thuộc vào cả mật độ và hình dạng của con lắc.
- Sức cản không khí nhớt làm chậm vận tốc của con lắc. Điều này có ảnh hưởng không đáng kể đến chu kỳ, nhưng gây tiêu tán năng lượng, làm giảm biên độ. Điều này làm hụt hệ số Q của con lắc, đòi hỏi lực truyền động lớn hơn từ cơ chế đồng hồ để giữ cho nó tiếp tục chuyển động, điều này gây ra sự nhiễu loạn gia tăng cho chu kỳ.
Tăng áp suất khí quyển làm tăng chu kỳ của con lắc một chút do hai hiệu ứng đầu tiên, khoảng 0,11 giây mỗi ngày trên mỗi kilopascal (0,37 giây mỗi ngày trên một inch thủy ngân hoặc 0,015 giây mỗi ngày trên torr).[58] Các nhà nghiên cứu sử dụng con lắc để đo gia tốc trọng trường phải điều chỉnh chu kỳ cho áp suất không khí ở độ cao đang đo, tính toán thời gian tương đương của một con lắc dao động trong chân không. Đồng hồ quả lắc được vận hành lần đầu tiên trong bể áp suất không đổi bởi Friedrich Tiede vào năm 1865 tại Đài thiên văn Berlin,[84][85] và đến năm 1900, đồng hồ có độ chính xác cao nhất được gắn trong các bể đẳng áp để loại bỏ những thay đổi trong áp suất không khí.
Ghi chú[sửa | sửa mã nguồn]
- ^ Một dao động "nhỏ" là một dao động mà góc θ đủ nhỏ để sin(θ) có thể lấy xấp xỉ bằng θ với θ được đo bằng đơn vị radian
Tham khảo[sửa | sửa mã nguồn]
- ^ “Pendulum”. Miriam Webster's Collegiate Encyclopedia. Miriam Webster. 2000. tr. 1241. ISBN 0-87779-017-5.
- ^ a b c Marrison, Warren (1948). “The Evolution of the Quartz Crystal Clock”. Bell System Technical Journal. 27: 510–588. Bản gốc lưu trữ ngày 17 tháng 7 năm 2011. Truy cập ngày 6 tháng 2 năm 2014.
- ^ Morris, William, Ed. (1979). The American Heritage Dictionary, New College Ed. New York: Houghton-Mifflin. tr. 969. ISBN 0-395-20360-0.
- ^ a b c d e f g h i Milham, Willis I. (1945). Time and Timekeepers. MacMillan., p.188-194
- ^ Halliday, David; Robert Resnick; Jearl Walker (1997). Fundamentals of Physics, 5th Ed. New York: John Wiley & Sons. tr. 381. ISBN 978-0-471-14854-8.
- ^ Cooper, Herbert J. (2007). Scientific Instruments. New York: Hutchinson's. tr. 162. ISBN 978-1-4067-6879-4.
- ^ a b Nelson, Robert; M. G. Olsson (tháng 2 năm 1987). “The pendulum – Rich physics from a simple system” (PDF). American Journal of Physics. 54 (2): 112–121. Bibcode:1986AmJPh..54..112N. doi:10.1119/1.14703. Truy cập ngày 29 tháng 10 năm 2008.
- ^ “Clock”. Encyclopædia Britannica, 11th Ed. 6. The Encyclopædia Britannica Publishing Co. 1910. tr. 538. Truy cập ngày 4 tháng 3 năm 2009. includes a derivation
- ^ Nave, Carl R. (2006). “Simple pendulum”. Hyperphysics. Georgia State Univ. Truy cập ngày 10 tháng 12 năm 2008.
- ^ Xue, Linwei (2007). “Pendulum Systems”. Seeing and Touching Structural Concepts. Civil Engineering Dept., Univ. of Manchester, UK. Truy cập ngày 10 tháng 12 năm 2008.
- ^ Weisstein, Eric W. (2007). “Simple Pendulum”. Eric Weisstein's world of science. Wolfram Research. Truy cập ngày 9 tháng 3 năm 2009.
- ^ Deschaine, J. S.; Suits, B. H. (2008). “The hanging cord with a real tip mass”. European Journal of Physics. 29 (6): 1211–1222. Bibcode:2008EJPh...29.1211D. doi:10.1088/0143-0807/29/6/010.
- ^ a b Huygens, Christian (1673). “Horologium Oscillatorium”. 17centurymaths. Bruce, Ian biên dịch. 17thcenturymaths.com. Truy cập ngày 1 tháng 3 năm 2009., Part 4, Proposition 5
- ^ Glasgow, David (1885). Watch and Clock Making. London: Cassel & Co. tr. 278.
- ^ Fowles, Grant R (1986). Analytical Mechanics, 4th Ed. NY, NY: Saunders. tr. 202 ff.
- ^ a b Huygens (1673) Horologium Oscillatorium, Part 4, Proposition 20
- ^ Morton, W. Scott và Charlton M. Lewis (2005). Trung Quốc: Lịch sử và Văn hóa. New York: McGraw-Hill, Inc., p. 70
- ^ a b Needham, Volume 3, 627-629
- ^ Good, Gregory (1998). Khoa học Trái Đất: Cuốn bách khóa về Sự kiện, Con người, và Hiện tượng. Routledge. tr. 394. ISBN 978-0-8153-0062-5.
- ^ “Con lắc”. Encyclopedia Americana. 21. The Americana Corp. 1967. tr. 502. Truy cập ngày 20 tháng 2 năm 2009.
- ^ Baker, Cyril Clarence Thomas (1961). Từ điển Toán học. G. Newnes. tr. 176.
- ^ Newton, Roger G. (2004). Galileo's Pendulum: From the Rhythm of Time to the Making of Matter. US: Harvard University Press. tr. 52. ISBN 978-0-674-01331-5.
- ^ King, D. A. (1979). “Ibn Yunus và con lắc: lịch sử sai sót”. Archives Internationales d'Histoire des Sciences. 29 (104): 35–52.
- ^ Hall, Bert S. (tháng 9 năm 1978). “The scholastic pendulum”. Annals of Science. 35 (5): 441–462. doi:10.1080/00033797800200371. ISSN 0003-3790.
- ^ O'Connor, J. J.; Robertson, E. F. (tháng 11 năm 1999). “Abu'l-Hasan Ali ibn Abd al-Rahman ibn Yunus”. University of St Andrews. Truy cập ngày 29 tháng 5 năm 2007.Quản lý CS1: sử dụng tham số tác giả (liên kết)
- ^ Matthews, Michael R. (2000). Time for science education. Springer. tr. 87. ISBN 978-0-306-45880-4.
- ^ a b Drake, Stillman (2003). Galileo at Work: His scientific biography. USA: Courier Dover. tr. 20–21. ISBN 978-0-486-49542-2.
- ^ Galilei, Galileo (1890–1909; reprinted 1929–1939 and 1964–1966). Favaro, Antonio (biên tập). Le Opere di Galileo Galilei, Edizione Nazionale [The Works of Galileo Galilei, National Edition] (bằng tiếng Ý). Florence: Barbera. ISBN 978-88-09-20881-0. Kiểm tra giá trị ngày tháng trong:
|date=(trợ giúp) - ^ Murdin, Paul (2008). Đỉnh cao của huy hoàng: Cuộc hành trình gian nguy trong cuộc thi để đo đạc Trái Đất. Springer. tr. 41. ISBN 978-0-387-75533-5.
- ^ La Lampada di Galileo, bởi Francesco Malaguzzi Valeri, cho Archivio storico dell'arte, Tập 6 (1893); Editor, Domenico Gnoli; Publisher Danesi, Rome; Trang 215-218.
- ^ a b c Van Helden, Albert (1995). “Đồng hồ Con lắc”. The Galileo Project. Rice Univ. Truy cập ngày 25 tháng 2 năm 2009.
- ^ Drake 2003, p.419–420
- ^ although there are unsubstantiated references to prior pendulum clocks made by others: Usher, Abbott Payson (1988). Lịch sử các Phát minh Cơ học. Courier Dover. tr. 310–311. ISBN 978-0-486-25593-4.
- ^ Eidson, John C. (2006). Phép đo, Điều khiển, và Giao tiếp sử dụng IEEE 1588. Burkhausen. tr. 11. ISBN 978-1-84628-250-8.
- ^ Milham 1945, p.145
- ^ a b O'Connor, J.J.; E.F. Robertson (tháng 8 năm 2002). “Robert Hooke”. Biographies, MacTutor History of Mathematics Archive. School of Mathematics and Statistics, Univ. of St. Andrews, Scotland. Bản gốc lưu trữ ngày 3 tháng 3 năm 2009. Truy cập ngày 21 tháng 2 năm 2009.
- ^ Nauenberg, Michael (2006). “Đóng góp sâu sắc của Robert Hooke cho nền cơ học quỹ đạo”. Robert Hooke: Tercentennial Studies. Ashgate Publishing. tr. 17–19. ISBN 0-7546-5365-X.
- ^ Nauenberg, Michael (2004). “Hooke và Newton: Tiên đoán chuyển động hành tinh”. Physics Today. 57 (2): 13. Bibcode:2004PhT....57b..13N. doi:10.1063/1.1688052. Truy cập ngày 30 tháng 5 năm 2007.
- ^ The KGM Group, Inc. (2004). “Các mô hình Nhật tâm”. Science Master. Bản gốc lưu trữ ngày 13 tháng 7 năm 2007. Truy cập ngày 30 tháng 5 năm 2007.
- ^ Lenzen, Victor F.; Robert P. Multauf (1964). “Paper 44: Development of gravity pendulums in the 19th century”. United States National Museum Bulletin 240: Contributions from the Museum of History and Technology reprinted in Bulletin of the Smithsonian Institution. Washington: Smithsonian Institution Press. tr. 307. Truy cập ngày 28 tháng 1 năm 2009.
- ^ Richer, Jean (1679). Observations astronomiques et physiques faites en l'isle de Caïenne. Mémoires de l'Académie Royale des Sciences. cited in Lenzen & Multauf, 1964, p.307
- ^ Lenzen & Multauf, 1964, p.307
- ^ Poynting, John Henry; Joseph John Thompson (1907). Sách giáo khoa của Vật lý, Tái bản lần 4. London: Charles Griffin & Co. tr. 20–22.
- ^ Huygens, Christian; translated by Ian Bruce (tháng 7 năm 2007). “Horologium Oscillatorium” (PDF). 17centurymaths. 17thcenturymaths.com. Truy cập ngày 1 tháng 3 năm 2009.
- ^ Chòm sao Horologium được đặt tên để tưởng nhớ thành tựu của cuốn sách này.
- ^ Matthews, Michael R. (1994). Giảng dạy Khoa học: Vài trò của Lịch sử và Triết lý trong Khoa học. Psychology Press. tr. 121–122. ISBN 978-0-415-90899-3.
- ^ Huygens, Horologium Oscillatorium, Part 2, Proposition 25
- ^ Mahoney, Michael S. (ngày 19 tháng 3 năm 2007). “Christian Huygens: Phép đo thời gian và kinh độ ngoài biển”. Đại học Princeton. Bản gốc lưu trữ ngày 4 tháng 12 năm 2007. Truy cập ngày 27 tháng 5 năm 2007.
- ^ Bevilaqua, Fabio; Lidia Falomo; Lucio Fregonese; Enrico Gianetto; Franco Giudise; Paolo Mascheretti (2005). “Con lắc: Từ sự rơi ràng buộc đến khái niệm thế năng”. Con lắc: Các góc nhìn Khoa học, Lịch sử, Triết học, và Khoa giáo. Springer. tr. 195–200. ISBN 1-4020-3525-X. Truy cập ngày 26 tháng 2 năm 2008. gives a detailed description of Huygen's methods
- ^ a b Beckett, Edmund (1874). Sơ luận về Đồng hồ và Đồng hồ đeo tay và Chuông (A Rudimentary Treatise on Clocks and Watches and Bells), tái bản lần thứ 6. London: Lockwood & Co. tr. 50.
- ^ a b Graham, George (1726). “Một mưu kế để tránh sự bất thường trong chuyển động của đồng hồ do tác động của nóng và lạnh lên thanh của con lắc”. Philosophical Transactions of the Royal Society. 34 (392–398): 40–44. doi:10.1098/rstl.1726.0006. cited in Day, Lance; Ian McNeil (1996). Từ điển Tiểu sử về Lịch sử của Công nghệ. Taylor & Francis. tr. 300. ISBN 978-0-415-06042-4.
- ^ Lỗi chú thích: Thẻ
<ref>sai; không có nội dung trong thẻ ref có tênAndrewes1994 - ^ Kater, Henry (1818). “Một phương án thí nghiệm để xác định [[chiều dài]] của con lắc dao động vài giây tại vĩ độ ở Luân Đôn”. Phil. Trans. R. Soc. 104 (33): 109. Truy cập ngày 25 tháng 11 năm 2008. Tựa đề URL chứa liên kết wiki (trợ giúp)
- ^ Rubin, Julian (tháng 9 năm 2007). “Phát kiến Con lắc Foucault”. Following the Path of Discovery. Truy cập ngày 31 tháng 10 năm 2007.
- ^ Amir Aczel (2003) Leon Foucault: His life, times and achievements, in Matthews, Michael R.; Colin F. Gauld; Arthur Stinner (2005). The Pendulum: Scientific, Historical, Educational, and Philosophical Perspectives. Springer. tr. 177. ISBN 978-1-4020-3525-8.
- ^ Giovannangeli, Françoise (tháng 11 năm 1996). “Con lắc quay tròn của Foucault tại Điện Panthéon”. The Paris Pages. Bản gốc lưu trữ ngày 9 tháng 6 năm 2007. Truy cập ngày 25 tháng 5 năm 2007.
- ^ Tobin, William (2003). Cuộc đời và thành tựu khoa học của Leon Foucault: Người chứng minh Trái Đất quay. UK: Cambridge University Press. tr. 148–149. ISBN 978-0-521-80855-2.
- ^ a b c d “Đồng hồ”. Encyclopædia Britannica, 11th Ed. 6. The Encyclopædia Britannica Publishing Co. 1910. tr. 540–541. Truy cập ngày 4 tháng 3 năm 2009.
- ^ Jones, Tony (2000). Chia nhỏ một giây: Câu chuyện của Thời gian Nguyên tử. CRC Press. tr. 30. ISBN 978-0-7503-0640-9.
- ^ Kaler, James B. (2002). Bầu trời đổi thay: Cẩm nang về Thiên cầu. UK: Cambridge Univ. Press. tr. 183. ISBN 978-0-521-49918-7.
- ^ Audoin, Claude; Bernard Guinot; Stephen Lyle (2001). Phép đo thời gian: Thời gian, Tần số, và Đồng hồ Nguyên tử. UK: Cambridge Univ. Press. tr. 83. ISBN 978-0-521-00397-1.
- ^ Torge, Wolfgang (2001). Trắc địa: Giới thiệu. Walter de Gruyter. tr. 177. ISBN 978-3-11-017072-6.
- ^ Milham 1945, p.334
- ^ tính toán từ phương trình (1)
- ^ Glasgow, David (1885). Cách làm đồng hồ và đồng hồ đeo tay. London: Cassel & Co. tr. 279–284.
- ^ Matthys, Robert J. (2004). Các đồng hồ con lắc chính xác. UK: Oxford Univ. Press. tr. 4. ISBN 978-0-19-852971-2.
- ^ Mattheys, 2004, p. 13
- ^ Matthys 2004, p.91-92
- ^ Beckett 1874, p.48
- ^ “Điều chỉnh”. Encyclopedia of Clocks and Watches. Old and Sold antiques marketplace. 2006. Truy cập ngày 9 tháng 3 năm 2009.
- ^ Beckett 1874, p.43
- ^ Glasgow 1885, p.282
- ^ “Great Clock facts”. Big Ben. London: UK Parliament. ngày 13 tháng 11 năm 2009. Bản gốc lưu trữ ngày 7 tháng 10 năm 2009. Truy cập ngày 31 tháng 10 năm 2012.
- ^ Matthys 2004, p.3
- ^ a b c d “Clock”. Encyclopædia Britannica, 11th Ed. 6. The Encyclopædia Britannica Publishing Co. 1910. tr. 539–540. Truy cập ngày 4 tháng 3 năm 2009.
- ^ Huygens, Christiaan (1658). Horologium (PDF). The Hague: Adrian Vlaqc., translation by Ernest L. Edwardes (December 1970) Antiquarian Horology, Vol.7, No.1
- ^ Zupko, Ronald Edward (1990). Revolution in Measurement: Western European Weights and Measures since the Age of Science. Diane Publishing. tr. 131. ISBN 978-0-87169-186-6.
- ^ Picard, Jean, La Mesure de la Terre [The measurement of the Earth] (Paris, France: Imprimerie Royale, 1671), p. 4. Picard described a pendulum consisting of a copper ball which was an inch in diameter and was suspended by a strand of pite, a fiber from the aloe plant. Picard then mentions that temperature slightly effects the length of this pendulum: "Il est vray que cette longueur ne s'est pas toûjours trouvées si précise, & qu'il a semblé qu'elle devoit estre toûjours un peu accourcie en Hyver, & allongée en esté; mais c'est seulement de la dixieme partie d'une ligne … " (Đúng là chiều dài này [của con lắc] không phải lúc nào cũng chính xác, và rằng có vẻ như nó bị ngắn đi vào mùa đông, và dài ra vào mùa hè; nhưng nó chỉ vào cỡ phần mười của một ligne [1 ligne (line) = 2.2558 mm] …)
- ^ a b c d Matthys 2004, p.7-12
- ^ Milham 1945, p.335
- ^ Milham 1945, p.331-332
- ^ Matthys 2004, Part 3, p.153-179
- ^ Poynting & Thompson, 1907, p.13-14
- ^ Updegraff, Milton (ngày 7 tháng 2 năm 1902). “On the measurement of time”. Science. 15 (371): 218–219. doi:10.1126/science.ns-15.374.218-a. PMID 17793345. Truy cập ngày 13 tháng 7 năm 2009.
- ^ Dunwoody, Halsey (1917). Notes, Problems, and Laboratory Exercises in Mechanics, Sound, Light, Thermo-Mechanics and Hydraulics, 1st Ed. New York: John Wiley & Sons. tr. 87.
Đọc thêm[sửa | sửa mã nguồn]
- G. L. Baker and J. A. Blackburn (2009). The Pendulum: A Case Study in Physics (Oxford University Press).
- M. Gitterman (2010). The Chaotic Pendulum (World Scientific).
- Michael R. Matthews, Arthur Stinner, Colin F. Gauld (2005)The Pendulum: Scientific, Historical, Philosophical and Educational Perspectives, Springer
- Michael R. Matthews, Colin Gauld and Arthur Stinner (2005) The Pendulum: Its Place in Science, Culture and Pedagogy. Science & Education, 13, 261-277.
- Matthys, Robert J. (2004). Accurate Pendulum Clocks. UK: Oxford Univ. Press. ISBN 0-19-852971-6.
- Nelson, Robert (tháng 2 năm 1986). M. G. Olsson. “The pendulum – Rich physics from a simple system” (PDF). American Journal of Physics. 54 (2): 112–121. Bibcode:1986AmJPh..54..112N. doi:10.1119/1.14703. Truy cập ngày 29 tháng 10 năm 2008.
- L. P. Pook (2011). Understanding Pendulums: A Brief Introduction (Springer).
Liên kết ngoài[sửa | sửa mã nguồn]
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Con lắc. |
- NAWCC National Association of Watch & Clock Collectors Museum
- Graphical derivation of the time period for a simple pendulum Lưu trữ 2015-07-11 tại Wayback Machine
- A more general explanation of pendula
- Web-based calculator of pendulum properties from numerical inputs
- An animated and interactive rigid pendulum model in MS Excel Lưu trữ 2012-03-06 tại Wayback Machine