Lân cận (toán học)

Trong tô-pô và những nhánh liên quan của toán học, một lân cận là một trong những khái niệm cơ bản của một không gian tôpô. Nó liên quan đến khái niệm của tập mở và phần trong. Một cách trực quan, một lân cận của một điểm là một tập các điểm chứa nó sao cho ta có thể di chuyển một khoảng cách nào đó theo một hướng bất kì từ điểm đó mà không rời khỏi tập hợp đang xét.
Định nghĩa[sửa | sửa mã nguồn]
Lân cận của một điểm[sửa | sửa mã nguồn]

Nếu X là một không gian tôpô và p là một điểm trong X, một lân cận của p là một tập con V của X bao một tập mở U chứa p,
Điều này tương đương với việc điểm p nằm trong V.
Để ý rằng lân cận V không nhất thiết là một tập mở. Nếu V là mở thì nó được gọi là một lân cận mở.[1] Tuy nhiên một số nhà toán học yêu cầu lân cận phải là tập mở, nên cần để ý quy ước.
Một tập A là lân cận của mọi điểm nó chứa là tập mở vì nó có thể biểu diễn thành hợp của những tập mở chứa mỗi điểm của A. Một hình chữ nhật, như trong hình minh họa, không phải là lân cận của tất cả những điểm của nó; những điểm trên các cạnh hay góc không nằm trong bất kỳ tập mở nào bao trong hình chữ nhật.
Tất cả các lân cận của một điểm được gọi là hệ lân cận tại điểm đó.
Lân cận của một tập hợp[sửa | sửa mã nguồn]
Nếu S là một tập con của không gian tôpô X thì một lân cận của S là tập V bao gồm một tập mở U chứa S. Từ đây ta suy ra rằng tập V là một lân cận của S khi và chỉ khi nó là lân cận của mọi điểm chứa trong S. Hơn thế nữa, V là lân cận của S khi và chỉ khi S là một tập con của phần trong của V. Lân cận của một điểm khi ấy là một trường hợp đặc biệt của định nghĩa này.
Trong một không gian mêtric[sửa | sửa mã nguồn]


Trong một không gian mêtric M = (X, d), một tập V là một lân cận của điểm p nếu tồn tại một hình cầu mở với tâm p và bán kính r0, sao cho
được chứa trong V.
V được gọi là lân cận đều của tập S nếu tồn tại một số dương r sao cho với mọi phần tử p thuộc S,
nằm trong V.
Với r > 0, lân cận r Sr của tập S là tập hợp tất cả các điểm thuộc X và cách S một khoảng bé hơn r (hay một cách tương đương, Sr là hợp của tất cả quả cầu mở bán kính r có tâm đặt tại một điểm thuộc S):
Hệ quả là một lân cận r là một lân cận đều, và một tập là một lân cận đều khi và chỉ khi nó chứa một lân cận r với một giá trị r nào đó.
Ví dụ[sửa | sửa mã nguồn]
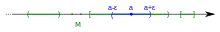
Xét tập số thực với mêtric Euclid và một tập con V định nghĩa bởi
- ,
khi ấy V là một lân cận cho tập các số tự nhiên , nhưng không phải là một lân cận đều của nó.
Định nghĩa tôpô bằng lân cận[sửa | sửa mã nguồn]
Định nghĩa trên hữu dụng khi khái niệm tập mở đã được định nghĩa. Có một cách khác để định nghĩa một tôpô, bằng cách định nghĩa hệ lân cận, sau đó tập mở là những tập chứa một lân cận của mọi điểm thuộc nó.
Một hệ lân cận trên X là việc gán filter N(x) (trên tập X) với mỗi x thuộc X, sao cho
- x là một phần tử của mọi U thuộc N(x)
- mọi U thuộc N(x) chứa một V thuộc N(x) sao cho với mọi y thuộc V, U thuộc N(y).
Có thể chứng minh rằng hai định nghĩa cả hai định nghĩa đều tương thích, nghĩa là tôpô nhận được từ hệ lân cận định nghĩa bằng tập mở, và ngược lại định nghĩa hệ lân cận như trên trước đều cho kết quả như nhau.
Lân cận thủng[sửa | sửa mã nguồn]
Một lân cận thủng của điểm p là một lân cận của p, nhưng không chứa {p}. Ví dụ, khoảng là một lân cận của p = 0 trên trục số thực, nên tập là một lân cận thủng của 0. Chú ý rằng một lân cận thủng của một điểm thực chất không phải là một lân cận của điểm đó. Khái niệm của lân cận thủng xuất hiện trong định nghĩa giới hạn của hàm số.
Xem thêm[sửa | sửa mã nguồn]
Tham khảo[sửa | sửa mã nguồn]
- ^ Dixmier, Jacques (1984). General Topology. Undergraduate Texts in Mathematics. Translated by Sterling K. Berberian. Springer. tr. 6. ISBN 0-387-90972-9.
According to this definition, an open neighborhood of x is nothing more than an open subset of E that contains x.
- Kelley, John L. (1975). General topology. New York: Springer-Verlag. ISBN 0-387-90125-6.
- Bredon, Glen E. (1993). Topology and geometry. New York: Springer-Verlag. ISBN 0-387-97926-3.
- Kaplansky, Irving (2001). Set Theory and Metric Spaces. American Mathematical Society. ISBN 0-8218-2694-8.









