Định luật Kirchhoff
Trong mạch điện, định luật Kirchhoff là hai phương trình để mô tả mối quan hệ của cường độ dòng điện và điện áp. Các định luật này được Gustav Kirchhoff xây dựng vào năm 1845.[1]
Định luật Kirchhoff về cường độ dòng điện[sửa | sửa mã nguồn]
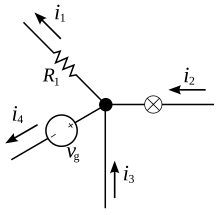
Định luật này còn được gọi là định luật Kirchhoff 1 (K1) hay định luật bảo toàn điện tích tại một nút, gọn lại là định luật nút.
Nguyên lý về bảo toàn điện tích bao hàm ý:
- Tại bất kỳ nút (ngã rẽ) nào trong một mạch điện, thì tổng cường độ dòng điện chạy đến nút phải bằng tổng cường độ dòng điện từ nút chạy đi, hay:
- Tổng giá trị đại số của dòng điện tại một nút trong một mạch điện là bằng không.
Công thức:
với n là tổng số các nhánh với dòng điện chạy vào nút hay từ nút ra.
Công thức theo dòng phức:
Định luật Kirchhoff về điện thế[sửa | sửa mã nguồn]
Định luật này còn gọi là định luật Kirchhoff 2 (K2) hay định luật bảo toàn điện áp trong một vòng, gọn lại là định luật vòng kín.
Cũng như định luật K1, định luật K2 phát biểu:
- Tổng giá trị điện áp dọc theo một vòng bằng 0.
Công thức:
với n là tổng số các điện áp được đo.
Công thức theo điệp áp phức:
Ví dụ[sửa | sửa mã nguồn]
Ví dụ mạch gồm 3 điện trở và 2 nguồn như hình:
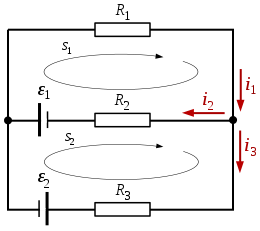
Theo định luật 1, ta có:
Định luật 2 áp dụng cho vòng s1:
Định luật 2 áp dụng cho vòng s2:
Đến đây ta có hệ phương trình tuyến tính cho 3 ẩn số :
Giả sử:
kết quả:
mang dấu âm vì hướng của ngược với hướng giả định trong hình.
Chú thích[sửa | sửa mã nguồn]
- ^ Oldham, Kalil T. Swain (2008). The doctrine of description: Gustav Kirchhoff, classical physics, and the "purpose of all science" in 19th-century Germany (Ph. D.). University of California, Berkeley. tr. 52. Docket 3331743. 3331743.
Liên kết ngoài[sửa | sửa mã nguồn]
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Định luật Kirchhoff. |
- MIT video lecture on the KVL and KCL methods












