Số phức

| Giải tích toán học → Giải tích phức |
| Giải tích phức |
|---|
 |
| Số phức |
| Hàm số phức |
| Lý thuyết cơ bản |
| Nhân vật |
Số phức (tiếng Anh: Complex number) là số có thể viết dưới dạng , trong đó a và b là các số thực, là đơn vị ảo, với hay .[1] Trong biểu thức này, số a gọi là phần thực, b gọi là phần ảo của số phức. Số phức có thể được biểu diễn trên mặt phẳng phức với trục hoành là trục số thực và trục tung là trục số ảo, do đó một số phức được xác định bằng một điểm có tọa độ (a,b). Một số phức nếu có phần thực bằng không thì gọi là số thuần ảo (số ảo), nếu có phần ảo bằng không thì trở thành số thực R. Việc mở rộng trường số phức để giải những bài toán mà không thể giải trong trường số thực.
Số phức được sử dụng trong nhiều lĩnh vực khoa học, như khoa học kỹ thuật, điện từ học, cơ học lượng tử, toán học ứng dụng chẳng hạn như trong lý thuyết hỗn loạn. Nhà toán học người Ý Gerolamo Cardano là người đầu tiên đưa ra số phức. Ông sử dụng số phức để giải các phương trình bậc ba trong thế kỉ 16.[2]
Lịch sử[sửa | sửa mã nguồn]
Nhà toán học người Ý R. Bombelli (1526-1573) đã đưa định nghĩa đầu tiên về số phức, lúc đó được gọi là số "không thể có" hoặc "số ảo" trong công trình Đại số (Bologne, 1572) công bố ít lâu trước khi ông mất. Ông đã định nghĩa các số đó (số phức) khi nghiên cứu các phương trình bậc ba và đã đưa ra căn bậc hai của .
Nhà toán học người Pháp D’Alembert vào năm 1746 đã xác định được dạng tổng quát "" của chúng, đồng thời chấp nhận nguyên lý tồn tại n nghiệm của một phương trình bậc n. Nhà toán học Thụy Sĩ L. Euler (1707-1783) đã đưa ra ký hiệu "" để chỉ căn bậc hai của , năm 1801 Gauss đã dùng lại ký hiệu này.
Tổng quan[sửa | sửa mã nguồn]
Số phức cho phép giải một phương trình nhất định mà không giải được trong trường số thực. Ví dụ, phương trình
không có nghiệm thực, vì bình phương của một số thực không thể âm. Các số phức cho phép giải phương trình này. Ý tưởng là mở rộng trường số thực sang đơn vị ảo với , vì vậy phương trình trên được giải. Trong trường hợp này các nghiệm là −1 + 3i và −1 − 3i, có thể kiểm tra lại nghiệm khi thế vào phương trình và với :
Thực tế không chỉ các phương trình bậc hai mà tất cả các phương trình đại số có hệ số thực hoặc số ảo với một biến số có thể giải bằng số phức.
Định nghĩa[sửa | sửa mã nguồn]
Số phức được biểu diễn dưới dạng , với a và b là các số thực và là đơn vị ảo, thỏa mãn điều kiện . Ví dụ là một số phức.
Số thực a được gọi là phần thực của ; số thực b được gọi là phần ảo của . Theo đó, phần ảo không có chứa đơn vị ảo: do đó b, không phải bi, là phần ảo.[3][4] Phần thực của số phức z được ký hiệu là Re(z) hay ℜ(z); phần ảo của phức z được ký hiệu là Im(z) hay ℑ(z). Ví dụ:
Do đó, nếu xét theo phần thực và phần ảo, một số phức z sẽ được viết là . Biểu thức này đôi khi được gọi là dạng Cartesi của z.
Một số thực a có thể được biểu diễn ở dạng phức là với phần ảo là 0. Số thuần ảo là một số phức được viết là với phần thực bằng 0. Ngoài ra, khi phần ảo âm, nó được viết là với thay vì , ví dụ thay vì .
Tập hợp tất cả các số phức hay trường số phức được ký hiệu là ℂ, hay . Có nhiều phương pháp xây dựng trường số phức một cách chặt chẽ bằng phương pháp tiên đề.
Gọi là trường số thực. Ký hiệu là tập hợp các cặp (a,b) với .
Trong , định nghĩa hai phép cộng và phép nhân như sau:
thì là một trường (xem cấu trúc đại số).
Ta có thể lập một đơn ánh từ tập số thực vào bằng cách cho mỗi số thực a ứng với cặp . Khi đó ... Nhờ phép nhúng, ta đồng nhất tập các số thực với tập con các số phức dạng , khi đó tập các số thực là tập con của tập các số phức và được xem là một mở rộng của .
Ký hiệu là cặp (0,1) . Ta có
.
Tất cả các số phức dạng được gọi là các số thuần ảo.
Một số khái niệm quan trọng trong trường số phức[sửa | sửa mã nguồn]
Dạng đại số của số phức[sửa | sửa mã nguồn]
Trong trường số phức, tính chất của đơn vị ảo đặc trưng bởi biểu thức
Mỗi số phức z đều được biểu diễn duy nhất dưới dạng:
trong đó a, b là các số thực. Dạng biểu diễn này được gọi là dạng đại số của số phức z.
Với cách biểu diễn dưới dạng đại số, phép cộng và nhân các số phức được thực hiện như phép cộng và nhân các nhị thức bậc nhất với lưu ý rằng . Như vậy, ta có:
Mặt phẳng phức[sửa | sửa mã nguồn]
Trong hệ toạ độ Descartes, có thể dùng trục hoành chỉ tọa độ phần thực còn trục tung cho tọa độ phần ảo để biểu diễn một số phức
Khi đó mặt phẳng tọa độ được gọi là mặt phẳng phức.
Số thực và số thuần ảo[sửa | sửa mã nguồn]
Mỗi số thực được xem là một số phức có .
Ta có:
Nếu , số phức được gọi là thuần ảo.
Số phức liên hợp[sửa | sửa mã nguồn]
Cho số phức dưới dạng đại số , số phức được gọi là số phức liên hợp của z.
Một số tính chất của số phức liên hợp:
- là một số thực.
- là một số thực
- =
- =
Module và Argument[sửa | sửa mã nguồn]
- Cho . Khi đó . Căn bậc hai của được gọi là module của z, ký hiệu là . Như vậy .
- Xem thêm: giá trị tuyệt đối
- Có thể biểu diễn số phức trên mặt phẳng tọa độ bằng điểm , góc giữa chiều dương của trục Ox và vec tơ được gọi là của số phức , ký hiệu là .
- Một vài tính chất của module và argument
Dạng lượng giác của số phức[sửa | sửa mã nguồn]
Định nghĩa[sửa | sửa mã nguồn]
Số phức có thể viết dưới dạng
Khi đặt
- ,
ta có
Cách biểu diễn này được gọi là dạng lượng giác của số phức .
Phép toán trên các số phức viết dưới dạng lượng giác[sửa | sửa mã nguồn]
Cho hai số phức dưới dạng lượng giác
Khi đó
- Lũy thừa tự nhiên của số phức dưới dạng lượng giác (công thức Moirve).
- Khai căn số phức dưới dạng lượng giác.
Mọi số phức z khác 0 đều có đúng n căn bậc n, là các số dạng
trong đó ,
Một số ứng dụng[sửa | sửa mã nguồn]
- Ứng dụng của số phức trong hình học phẳng: phép quay 90 độ có bình phương bằng -1. Quay hai lần 90 độ thì bằng quay 180 độ, mà quay 180 độ có nghĩa là lấy điểm ngược lại, cũng có nghĩa là nhân với -1. Vậy ta có thể nói rằng số ảo đại diện cho sự quay, sự chuyển hướng 90 độ. Chính vì " chẳng qua là quay 90 độ" nên số phức rất hiệu nghiệm trong hình học phẳng và trong lượng giác. Nhiều vấn đề của hình học phẳng rất phức tạp, hay nhiều công thức lượng giác phức tạp, trở nên đơn giản hơn hẳn khi sử dụng số phức để giải quyết.
- Phân tích đa thức thành nhân tử.
- Tính toán các tích phân.
- Tìm dạng chuẩn và phân loại các cấu trúc toán học.
- Trong vật lý ngày nay, số phức xuất hiện rất nhiều. Bởi vì vật lý liên quan đến hình học, có nhiều đại lượng không chỉ có độ lớn mà còn có hướng. Mà đã nói đến hướng là dễ đụng đến số phức, vì số ảo thể hiện sự quay 90 độ. Ví dụ như để mô tả dòng điện xoay chiều (là thứ điện ta dùng chủ yếu ngày nay) hay một số thứ trong mạng điện nói chung, người ta có thể dùng số phức.
Các tập hợp số[sửa | sửa mã nguồn]
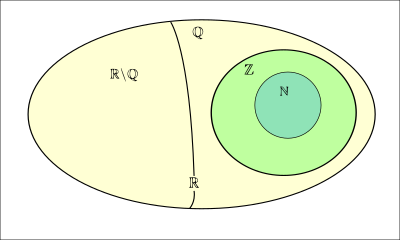
- : Tập hợp số tự nhiên
- : Tập hợp số nguyên
- : Tập hợp số hữu tỉ
- : Tập hợp số vô tỉ
- : Tập hợp số thực
- : Tập hợp số phức
Xem thêm[sửa | sửa mã nguồn]
- Hình học phức
- Mặt cầu Riemann (mặt phẳng phức mở rộng)
- Giải tích phức
- Số siêu phức
- Số nguyên Gauss
- Căn bậc hai
- Công thức Euler
Chú thích[sửa | sửa mã nguồn]
- ^ Charles P. McKeague (2011). Elementary Algebra. Brooks/Cole. tr. 524. ISBN 978-0-8400-6421-9.
- ^ Burton (1995, tr. 294)
- ^ Complex Variables (2nd Edition), M.R. Spiegel, S. Lipschutz, J.J. Schiller, D. Spellman, Schaum's Outline Series, Mc Graw Hill (USA), ISBN 978-0-07-161569-3
- ^ Aufmann, Richard N.; Barker, Vernon C.; Nation, Richard D. (2007), College Algebra and Trigonometry (ấn bản 6), Cengage Learning, tr. 66, ISBN 0-618-82515-0, Chapter P, p. 66
Liên kết ngoài[sửa | sửa mã nguồn]
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Số phức. |
- Số phức tại Encyclopædia Britannica (tiếng Anh)
| Các chủ đề chính trong toán học |
|---|
| Nền tảng toán học | Đại số | Giải tích | Hình học | Lý thuyết số | Toán học rời rạc | Toán học ứng dụng | Toán học giải trí | Toán học tô pô | Xác suất thống kê |







![{\displaystyle {\big [}\left(-1+3i\right)+1{\big ]}^{2}=\left(3i\right)^{2}=\left(3^{2}\right)\left(i^{2}\right)=9\cdot \left(-1\right)=-9}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07da03dc7cbb4d94418abdd4e3884770d3c034aa)
![{\displaystyle {\big [}\left(-1-3i\right)+1{\big ]}^{2}=\left(-3i\right)^{2}=\left(-3\right)^{2}\left(i^{2}\right)=9\cdot (-1)=-9}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c5334849aa929fb370d05e4c73e2940764c0042)



































































![{\displaystyle {\omega }_{k}={\sqrt[{n}]{r}}\left(\cos {\psi }_{k}+i\sin {\psi }_{k}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a03dd7d07b639e386d3e187aac1866ee12ba466b)





