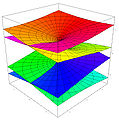
Mặt Riemann

Trong toán học, mặt Riemann (hay còn gọi là diện Riemann), đặt tên theo nhà toán học Bernhard Riemann, là đa tạp phức một chiều. Mặt Riemann có thể được xem là những bản uốn cong của mặt phẳng phức: ở lân cận mỗi điểm chúng giống nhau là một mảnh trên mặt phẳng phức, nhưng tô pô toàn cục có thể khác. Ví dụ, chúng có thể giống mặt cầu hoặc mặt xuyến hoặc một số tấm dán lại với nhau.
Định nghĩa[sửa | sửa mã nguồn]
Một mặt Riemann là một không gian tô pô Hausdorff X, với một át-lát vào C sao cho các phép biến đổi bản đồ là các hàm song chỉnh hình. Tức là X có một phủ mở (Ui) gồm các tập mở đồng phôi với các tập mở của C sao cho các ánh xạ đồng phôi thỏa mãn là một hàm song chỉnh hình.
Mặt cầu Riemann[sửa | sửa mã nguồn]
Xét . Gán cho nó hai hệ tọa độ (hay hai bản đồ) phức và . Hàm đổi hệ tọa độ là hàm , là một hàm song chỉnh hình. Đây được gọi là mặt cầu Riemann (dựa theo phép đồng phôi giữa mặt cầu với compắc hóa Alexandroff của mặt phẳng phức).
Mặt xuyến phức[sửa | sửa mã nguồn]
Mặt xuyến phức thường được định nghĩa là thương số của dưới tác động của một lưới với một số phức có phần ảo lớn hơn .
Các mặt Riemann ứng với một hàm số[sửa | sửa mã nguồn]
Xét một hàm số . Không phải lúc nào cũng tồn tại một hàm ngược của . Tuy nhiên có thể được định nghĩa như một hàm trên một mặt Riemann tương ứng với nó. Sau đây là các mặt Riemann ứng với lần lượt bằng (và các hàm ngược tương ứng ).
Hàm chỉnh hình[sửa | sửa mã nguồn]
Một hàm số phức trên một mặt Riemann được gọi là một hàm chỉnh hình nếu là một hàm chỉnh hình với mọi bản đồ của . Tương tự, một hàm số phức bộ phận được gọi là một hàm phân hình nếu là một hàm phân hình với mọi bản đồ của .
Cấu trúc vi phân[sửa | sửa mã nguồn]
Một mặt Riemann có một cấu trúc vi phân cảm sinh từ cấu trúc vi phân của mặt phẳng phức, là một đa tạp vi phân hai chiều.
Xem thêm[sửa | sửa mã nguồn]
Tham khảo[sửa | sửa mã nguồn]
- Forster, Otto, 1981, Lectures on Riemann Surfaces