Đa thức
Trong toán học, đa thức là biểu thức bao gồm các biến và các hệ số, và chỉ dùng các phép cộng, phép trừ, phép nhân, và lũy thừa với số mũ tự nhiên của các biến. Một ví dụ về đa thức trong biến x là x2 − 4x + 3. Ví dụ về đa thức có ba biến là x2 + 3xyz2 − yz + 1. Các phần tử trong đa thức được gọi là hạng tử. Trong hai ví dụ trước, x2 đều là hạng tử của đa thức.
Đa thức xuất hiện trong nhiều lĩnh vực của khoa học và toán học. Ví dụ chẳng hạn, chúng được dùng để lập các phương trình đa thức cho phép mã hoá rất nhiều bài toán mới, từ những bài toán từ sơ cấp cho đến các bài toán phức tạp trong khoa học; Các đa thức còn được dùng để định nghĩa hàm đa thức xuất hiện trong nhiều bối cảnh trong khoa học, từ hoá học và vật lý cơ bản cho đến kinh tế học và khoa học xã hội. Trong toán học cao cấp, các đa thức được dùng để xây vành đa thức và đa tạp đại số, là các khái niệm trung tâm trong đại số hiện đại và hình học đại số.
Ký hiệu và thuật ngữ[sửa | sửa mã nguồn]

Đa thức P trong biến x thường được ký hiệu là P hoặc P(x) (chữ cái P được lấy từ polynomial). Thường thì ta hay dùng P để ký hiệu cho đa thức, chứ không P(x). Song việc dùng ký hiệu hàm P(x) đã có từ thời mà sự phân biệt giữa đa thức và hàm gắn liền vẫn còn chưa rõ. Ký hiệu hàm vẫn được dùng khi muốn nói trong một lời về đa thức và biến của nó. Ví dụ, câu "gọi P(x) là đa thức" có thể hiểu ngay là "gọi P là đa thức trong biến x". Mặt khác, nhiều công thức trở nên dễ nhìn và dễ đọc hơn khi bỏ đi tên các biến trong đa thức.
Ngoài ra, lợi dụng tính tổng quát đằng sau ký hiệu hàm của đa thức, ta có thể dùng ký hiệu ánh xạ cho đa thức. Nếu a là một số, hay một biến, hay một đa thức hoặc tổng quát hơn là bất kỳ biểu thức khác thì P(a) là kết quả khi thay a cho x vào trong P. Do đó đa thức P định nghĩa hàm số sau:
được gọi là hàm đa thức gắn với P. Thường thì khi dùng sử dụng ký hiệu, ta thường coi a là số. Tuy nhiên, ta có thể dùng nó trên bất cứ miền nào có phép cộng và phép nhân được định nghĩa (tức là trên một vành). Đặc biệt là, nếu a là đa thức thì P(a) cũng là đa thức.
Định nghĩa[sửa | sửa mã nguồn]
Biểu thức đa thức là biểu thức được xây từ các hằng số và các ký hiệu chữ số được gọi là biến và được nối với nhau bằng các phép cộng, phép nhân. Các biến trong đa thức có thể được mũ lên số nguyên không âm. Hằng số thường là các con số nói chung, nhưng cũng có thể biểu diễn các đối tượng toán học khác cũng có thể nhân và cộng với biến và các hằng số còn lại. Hai biểu thức đa thức được gọi là biểu diễn chung một đa thức nếu một trong hai cái có thể biến đổi về cái còn lại qua việc sử dụng các tính chất của giao hoán, kết hợp và phân phối của phép cộng và phép nhân. Lấy ví dụ, và là hai biểu thức đa thức biểu diễn chung một đa thức; do đó ta có đẳng thức sau: .
Đa thức trong một biến x luôn có thể viết (hoặc viết lại) dưới dạng sau
trong đó là các hằng số được gọi là hệ số của đa thức, còn được gọi là biến số (hay nói gọn là biến).[1] Từ "biến số" có nghĩa là không biểu diễn không một giá trị cụ thể nào cả, mà thay và đó có thể thay bất kỳ giá trị vào trong đó. Ánh xạ giữa giá trị thay vào và kết quả của đa thức sau khi thay giá trị đó vào được gọi là hàm số, cụ thể hơn là hàm đa thức.
Công thức trên có thể viết gọn lại bằng ký hiệu sigma:
Nhìn vào trong đây, một đa thức có thể bằng có thể bằng không hoặc là tổng của hữu hạn số các đơn thức khác không. Mỗi đơn thức là tích của một hằng số, được gọi là hệ số của đơn thức đó[a] – và hữu hạn các biến khác, mỗi biến có thể được mũ lên một số nguyên không âm.
Phân loại[sửa | sửa mã nguồn]
Số mũ của một biến trong phần tử được gọi là bậc của biến đó trong cùng phần tử đó; bậc của một phần tử trong đa thức là tổng các bậc của các biến trong phần tử đó, và bậc của đa thức là bậc lớn nhất của các phần tử có hệ số khác không.[2] Bởi x = x1, bậc của biến không viết số mũ ở trên đầu là một.
Đơn thức không có biến và đa thức không có biến được gọi tương ứng là phần tử hằng và đa thức hằng.[b] Bậc của đơn thức hằng và đa thức hằng khác không luôn bằng 0. Bậc của đa thức không, tức 0 (không có đơn thức nào) thường được coi là không có bậc.[3]
Lấy ví dụ:
là một đơn thức có hệ số bằng −5 và các biến là x và y, trong đó bậc của x bằng hai, còn bậc của y bằng một. Vì bậc của đơn thức là tổng các bậc các biến trong đơn thức đó, nên trong ví dụ này, bậc của đơn thức đó là 2 + 1 = 3.
Tổng của các đơn thức lập thành một đa thức. Ví dụ sau là một đa thức:
Nó có ba đơn thức: đơn thức đầu tiên có bậc hai, đơn thức thứ hai có bậc một, và đơn thức cuối có bậc không.
Có hai đa thức bậc nhỏ có tên riêng của nó. Đa thức bậc không được gọi là đa thức hằng, hay nói gọn đi là hằng số. Đa thức bậc một có tên gọi khác là đa thức tuyến tính.[2] Tên của đa thức cũng có thể dùng cho đơn thức. Lấy ví dụ,đơn thức 2x trong x2 + 2x + 1 là đơn thức tuyến tính trong đa thức bậc hai.
Đa thức 0 là đa thức không có đơn thức nào trong đó, được gọi là đa thức không. Không giống các đa thức khác, bậc của nó không có giá trị cụ thể, mà thay vào đó bậc của nó thường được để không xác định, hoặc được định nghĩa là âm (hoặc là −1 hoặc −∞).[4] Đa thức không cũng là đa thức duy nhất trong một biến có vô số nghiệm. Đồ thị của đa thức không, tức f(x) = 0, là trục hoành.
Trong các đa thức có nhiều hơn một đơn thức, một đa thức được gọi là thuần nhất bậc n nếu tất cả các đơn thức của nó đều có bậc n. "Đa thức không" là đa thức thuần nhất nhưng không có bậc.[c] Ví dụ, x3y2 + 7x2y3 − 3x5 là đa thức thuần nhất bậc 5. Xem thêm đa thức thuần nhất.
Luật giao hoán của phép cộng được dùng để xếp lại tuỳ ý vị trí các đơn thức trong đa thức. Trong các đa thức một biến, các đơn thức thường được xếp theo thứ tự tăng dần hoặc giảm dần của các bậc. Ví dụ chẳng hạn, đa thức 3x2 - 5x + 4 được viết theo thứ tự giảm dần của bậc x. Đơn thức đầu tiên có hệ số bằng 3 và số bậc bằng 2. Vì bậc của đa thức khác không là bậc lớn nhất và cũng bởi đa thức này đã được viết theo thứ tự giảm dần, nên đa thức này có bậc bằng hai.[5]
Nếu trong đa thức có hai hay nhiều đơn thức có các biến giống nhau và được nâng lên cùng số mũ thì chúng có thể gộp lại với nhau thành một đơn thức dưới luật phân phối. Hệ số của đơn thức đó sẽ là tổng của các đơn thức kia cộng lại. Giá trị của hệ số đó có thể bằng 0.[6] Các đa thức có thể được phân loại bằng số đơn thức khác không của nó, đa thức có một đơn thức được gọi là đơn thức,[d] đa thức có hai đơn thức được gọi là nhị thức, và đa thức có ba đơn thức được gọi là tam thức. Thuật ngữ "tứ thức" rất ít dùng cho đa thức có bốn phần tử.
Đa thức thực là đa thức có các hệ số là số thực. Nếu nó dùng để định nghĩa hàm số nói chung, thì miền của nó không bị giới hạn. Tuy nhiên, nếu nói rõ là hàm đa thức thực, thì hàm này là hàm từ tập các số thực sang các số thực được định nghĩa bởi đa thức thực. Tương tự như vậy, đa thức nguyên là đa thức có hệ số nguyên, và đa thức phức là đa thức có hệ số phức.
Tính đa thức là thay các giá trị vào các biến của đa thức rồi thực hiện các phép cộng và nhân để tìm ra giá trị của đa thức đó. Đối với các đa thức chỉ có một biến, việc tính toán thường hiệu quả hơn (tức ít số lần phải tính toán hơn) khi dùng phương pháp Horner:
Số học[sửa | sửa mã nguồn]
Phép cộng và phép trừ[sửa | sửa mã nguồn]
Các đa thức có thể cộng với nhau bằng cách sử dụng luật kết hợp (để nhóm lại các đơn thức với nhau), và luật giao hoán (để sắp xếp lại các vị trí các đơn thức) của phép cộng rồi gộp chúng lại với nhau.[6][7] Lấy ví dụ, nếu
- và
thì tổng
có thể xếp và nhóm lại thành
sau đó rút gọn đi được
Tổng của các đa thức luôn là một đa thức.[8]
Trừ của đa thức cũng tương tự như vậy.
Phép nhân[sửa | sửa mã nguồn]
Các đa thức có thể nhân được với nhau. Để tính của tích của hai đa thức, ta có thể dùng tính phân phối để nhân từng đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng chúng lại cho nhau.[6] Ví dụ, nếu
thì
Tính phép nhân trong mỗi đơn thức được
Cộng các đơn thức lại với nhau thành
sau đó rút gọn đi thành
Tích của các đa thức luôn là một đa thức, được minh hoạ bởi ví dụ này.[3][8]
Phép hợp[sửa | sửa mã nguồn]
Cho đa thức có một biến và đa thức g có nhiều biến, thì hợp thu được bằng cách thay đa thức vào biến của đa thức .[3] Lấy ví dụ, nếu và thì
Phép chia[sửa | sửa mã nguồn]
Kết quả của đa thức chia đa thức chưa chắc cũng là đa thức. Thay vì đó kết quả ra được thường là phân thức, được gọi là phân thức hữu tỉ hoặc biểu thức hữu tỉ. Nếu dùng làm định nghĩa của hàm số thì hàm đó được gọi là hàm phân thức.[10] Cái này tương tự với phép chia số nguyên là số hữu tỉ, chứ không phải luôn là số nguyên.[11][12] Lấy ví dụ, phân thức 1/(x2 + 1) không phải đa thức, và nó không thể viết thành tổng các đơn thức biến x.
Đối với các đa thức một biến, ta có thể dùng phép chia Euclid của đa thức , phép chia này là dạng tổng quát của phép chia có dư của các số nguyên.[e] Phép chia a(x)/b(x) sẽ ra hai đa thức, thương q(x) và phần dư r(x), sao cho a = b q + r và degree(r) < degree(b) (degree(f) là bậc của đa thức f ). Thương và phần dư có thể được tính bằng một số thuật toán, bao gồm chia đa thức lớn và chia tổng hợp.[13]
Khi mẫu số b(x) monic và tuyến tính, tức là b(x) = x − c cho một số hằng số c, thì định lý phần dư đa thức khẳng định rằng phần dư của phép chia a(x) bởi b(x) là kết quả của a(c).[12] Trong trường hợp này, thương có thể tính theo quy tắc Ruffini, một trường hợp đặc biệt của phép chia.[14]
Phân tích[sửa | sửa mã nguồn]
Tất cả các đa thức có hệ số nằm trong miền phân tích duy nhất (ví dụ như tập các số nguyên hoặc trên một trường) đều viết thành tích của các đa thức bất khả quy và một hằng số. Dạng nhân tử này là duy nhất theo thứ tự của các thừa số và phép nhân của chúng với một hằng số khả nghịch.Trong trường của các số phức, các phần tử bất khả quy đều tuyến tính. Trên các số thực, thì các đa thức có bậc một và hai. Còn khi trên tập các số nguyên và tập các số hữu tỉ, các phần tử bất khả quy có thể có bậc bất kỳ.[15] Lấy ví dụ, dạng nhân tử của
là
trên tập số nguyên và tập số thực, và là
trên các số phức.
Việc tìm dạng tích của các đa thức này được gọi là phân tích nhân tử, và thường thì rất khó để có thể tự tính tay được phân tích của một đa thức tuỳ ý. Tuy nhiên, đã có sẵn các thuật toán phân tích đa thức hiệu quả trong phần lớn các hệ thống đại số máy tính.
Tích phân[sửa | sửa mã nguồn]
Tính đạo hàm và nguyên hàm của hàm đa thức rất là dễ so với các hàm số còn lại. Đạo hàm của đa thức
Đối với các đa thức mà hệ số của nó là các đối tượng toán học khác (ví dụ như hệ số là các số nguyên modulo một số nguyên tố p nào đó,hoặc là phần tử của một vành nào đó), công thức cho đạo hàm vẫn được hiểu và tính như thường, với hệ số kak được hiểu là tổng của k hệ số ak. Lấy ví dụ chẳng hạn, trên tập các số nguyên modulo p, đạo hàm của đa thức xp + x là đa thức 1.[16]
Hàm đa thức[sửa | sửa mã nguồn]
Hàm đa thức là hàm số được định nghĩa bằng đa thức. Chuẩn xác hơn, hàm f với một tham số từ một miền cho trước là hàm đa thức nếu tồn tại đa thức
tính ra giá trị cho mọi x nằm trong miền của f (trong đây, n là số nguyên không âm và a0, a1, a2, ..., an là các hệ số hằng). Trong tổng quát, trừ phi được nhắc trước thì các hàm đa thức sẽ có hệ số, tham số và giá trị đều là số phức.Cụ thể hơn, đa thức giới hạn hệ số thực vẫn sẽ định nghĩa hàm từ tập số phức sang tập số phức. Nếu thêm vào đó, miền của hàm số bị giới hạn về số thực, thì hàm số sẽ ánh xạ tập các số thực sang tập các số thực.
Lấy ví dụ, hàm f, định nghĩa như sau
là hàm đa thức một biến. Các hàm đa thức nhiều biến cũng có thể được định nghĩa tương tự
Theo định nghĩa hàm đa thức, có các biểu thức tuy không phải đa thức nhưng vẫn có thể dùng để định nghĩa hàm đa thức. Ví dụ biểu thức có cùng giá trị với đa thức trên đoạn , và do đó cả hai định nghĩa cùng một đa thức trên đoạn này.
Mọi hàm đa thức đều liên tục, trơn, và nguyên.
Đồ thị[sửa | sửa mã nguồn]
-
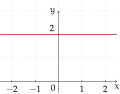
Đa thức bậc 0:
f(x) = 2 -
Đa thức bậc 1:
f(x) = 2x + 1 -
Đa thức bậc 2:
f(x) = x2 − x − 2
= (x + 1)(x − 2) -
Đa thức bậc 3:
f(x) = x3/4 + 3x2/4 − 3x/2 − 2
= 1/4 (x + 4)(x + 1)(x − 2) -
Đa thức bậc 4:
f(x) = 1/14 (x + 4)(x + 1)(x − 1)(x − 3)
+ 0.5 -
Đa thức bậc 5:
f(x) = 1/20 (x + 4)(x + 2)(x + 1)(x − 1)
(x − 3) + 2 -
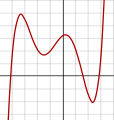
Đa thức bậc 6:
f(x) = 1/100 (x6 − 2x 5 − 26x4 + 28x3
+ 145x2 − 26x − 80) -
Đa thức bậc 7:
f(x) = (x − 3)(x − 2)(x − 1)(x)(x + 1)(x + 2)
(x + 3)
Ví dụ các đồ thị của các đa thức thực có một biến.
- Đồ thị của đa thức không là trục hoành.
- Đồ thị của đa thức bậc 0 là đường thẳng song song với trục hoành và cắt trục y tại a0
- Đồ thị của đa thức bậc 1 (hay hàm số tuyến tính) là đường thẳng cắt trục y tại a0 và có hệ số góc bằng với a1.
- Đồ thị của đa thức bậc 2 là đường parabol.
- Đồ thị của đa thức bậc 3 là đường cong bậc ba.
- Đồ thị của bất kỳ đa thức bậc hai hoặc lớn hơn là đường cong liên tục và không tuyến tính.
Hàm đa thức không hằng chạy tới vô cực khi mà giá trị cũng chạy tới vô cực (trong giá trị tuyệt đối). Nếu đa thức có bậc lớn một, thì đa thức không có tiệm cận.
Đồ thị đa thức được phân tích trong giải tích bằng các giao điểm, hệ số góc, tính lồi và hành vi cuối.
Phương trình[sửa | sửa mã nguồn]
Phương trình đa thức, hay còn gọi là phương trình đại số, là phương trình có dạng sau[17]
Lấy ví dụ,
là phương trình đại số.
Khi xét phương trình, các biến của đa thức lúc này sẽ được gọi là ẩn số (hay gọi gọn đi là ẩn), và các nghiệm là các giá trị cho ẩn sao cho đẳng thức đúng (thường thì có thể nhiều hơn một nghiệm). Phương trình đa thức khác với đồng nhất đa thức, trong đó đồng nhất đa thức là đẳng thức của hai đa thức bằng nhau, ví dụ như (x + y)(x − y) = x2 − y2.
Trong đại số sơ cấp, các phương pháp như công thức bậc hai được dùng để giải các phương trình một ẩn với bậc nhất và bậc hai. Ngoài ra còn có công thức giải cho các phương trình bậc ba và các phương trình bậc bốn. Đối với các bậc cao hơn, định lý Abel–Ruffini nói rằng không có công thức để giải cho phương trình bậc cao hơn bốn mà chỉ được dùng căn. Ta có thể dùng các thuật toán tìm nghiệm để tính xấp xỉ các nghiệm của bất kỳ biểu thức đa thức với bậc tuỳ ý.
Số các nghiệm của phương trình đa thức có hệ số thực luôn không vượt quá bậc của đa thức đó. Nếu nghiệm đó là nghiệm phức thì số nghiệm (đếm luôn cả lần lặp) luôn bằng với bậc của đa thức. Tính chất này là định lý cơ bản của đại số.
Giải phương trình[sửa | sửa mã nguồn]
Nghiệm của đa thức một biến khác không P là giá trị a của x sao cho P(a) = 0. Nói cách khác, nghiệm của P là nghiệm của phương trình đa thức P(x) = 0 hoặc là không điểm của hàm số của hàm đa thức định nghĩa bởi P. Trong trường hợp của đa thức không, mọi số đều là không điểm của hàm tương ứng và do đó ít khi quan tâm tới nghiệm của đa thức này.
Số a là nghiệm của đa thức P khi và chỉ khi đa thức tuyến tính x − a là ước của P, nghĩa là tồn tại ma trận Q sao cho P = (x − a) Q. Nếu P là đa thức khác không, thì tồn tại số mũ m cao nhất sao cho (x − a)m là ước của P, được gọi là số bội của a khi là ước của P. Số nghiệm của đa thức P, khi đếm cả số bội, không bao giờ vượt quá bậc của P,[18] và chỉ bằng với bậc này nếu xét tất cả nghiệm phức (đây là hệ quả của định lý cơ bản của đại số). Các hệ số và các nghiệm của đa thức có liên hệ với nhau qua các công thức Vieta.
Một số đa thức, ví dụ như x2 + 1, không có nghiệm trong tập các số thực. Nếu ta chấp nhận cả các số phức, mọi đa thức không hằng đều có ít nhất một nghiệm, điều này nằm trong định lý cơ bản của đại số. Bằng cách liên tục chia cho x − a, ta có thể thấy mọi đa thức với hệ số phức đều có thể viết thành tích của một hằng số với tích các đa thức có bậc một; và bởi vậy, số nghiệm phức đếm với số bội của nó luôn bằng với bậc của đa thức.
Khi giải phương trình, ta thường muốn biểu diễn nghiệm là một con số cụ thể; ví dụ, nghiệm duy nhất của 2x − 1 = 0 là 1/2. Tuy nhiên, không thể nào cũng có nghiệm duy nhất khi giải cho các phương trình có bậc cao hơn một. Ngay từ thời cổ đại , các nhà toán học đã tìm các biểu thức đại số để biểu diễn cho nghiệm; lấy ví dụ: tỷ lệ vàng là nghiệm dương duy nhất của Trong thời cổ đại, họ mới chỉ tìm được các biểu thức cho phương trình bậc nhất và bậc hai. Đối với các phương trình bậc hai, công thức bậc hai cho phép tìm ra các biểu thức của nghiệm. Kể từ thế kỉ 16 trở đi, các công thức tương tự (sử dụng thêm cả căn bậc ba với căn bậc hai), mặc dù phức tạp hơn nhưng đã được tìm thấy cho các phương trình bậc ba và bậc bốn (xem phương trình bậc ba và phương trình bậc bốn). Song, việc tìm kiếm công thức cho các phương trình bậc năm trở lên đã gây nhiều khó khăn cho các nhà nghiên cứu. Vào năm 1824, Niels Henrik Abel đã chứng minh rằng tồn tại các phương trình bậc 5 mà nghiệm của nó không thể biểu diễn bằng một công thức hữu hạn các phần tử và chỉ bao gồm các phép số học và phép căn (xem định lý Abel–Ruffini). Trong 1830, Évariste Galois đã chứng minh rằng phần lớn các phương trình có bậc lớn hơn bốn không thể nào chỉ giải được bằng căn, và chứng minh rằng với mỗi phương trình, ta đều có thể quyết định xem nó có giải được bằng căn không và nếu được thì giải nó.Kết quả đánh dấu sự khởi đầu của lý thuyết Galois và lý thuyết nhóm, hai nhánh quan trọng trong đại số hiện đại. Chính Galois đã tự nhận rằng các tính toán từ phương pháp của ông chưa ứng dụng được, song nay đã có công thức giải cho các phương trình giải được bậc năm và bậc sáu (xem phương trình bậc năm và phương trình bậc sáu).
Nếu mà không có công thức đại số để tìm ra nghiệm, hoặc có công thức nhưng nó lại quá phức tạp để có thể áp dụng vào, thì thay vì đó ta nên tính xấp xỉ giá trị nghiệm.[19] Có rất nhiều phương pháp để tính; một số được giới hạn chỉ giải cho đa thức và một số có thể giải cho hàm liên tục tuỳ ý. Các thuật toán tối ưu cho phép giải các đa thức (trong máy tính) có bậc lên tới hơn 1,000 (xem thuật toán tìm nghiệm).
Đối với các đa thức có nhiều hơn một biến, tổ hợp các giá trị sao cho hàm đa thức có giá trị 0 thường được gọi là không điểm thay vì "nghiệm". Nghiên cứu các tập không điểm của các đa thức là đối tượng của hình học đại số. Đối với hệ các phương trình đa thức nhiều biến, có các thuật toán có thể quyết định liệu nó có hữu hạn số nghiệm phức và nếu số nghiệm hữu hạn thì có thể tìm ra các nghiệm. Xem hệ phương trình đa thức.
Trường hợp đặc biệt mà hệ các phương trình đa thức đều có bậc một được gọi là hệ phương trình tuyến tính. Có rất nhiều phương pháp giải hệ phương trình này, bao gồm cả khử Gauss.
Phương trình đa thức mà ta chỉ quan tâm đến nghiệm nguyên được gọi là phương trình Diophantos. Giải phương trình Diophantos là bài toán rất là khó. Nó đã được chứng minh là không có thuật toán chung nào để giải, hoặc thậm chí là quyết định xem tập nghiệm có rỗng hay không (xem bài toán thứ 10 của Hilbert). Một số bài toán nổi tiếng được giải trong 50 năm gần đây có liên hệ với phương trình Diophantos, ví dụ như định lý lớn Fermat.
Các biểu thức đa thức khác[sửa | sửa mã nguồn]
Các đa thức sau có biến được thay bởi đối tượng toán học khác và do đó có tên riêng của nó.
Đa thức lượng giác[sửa | sửa mã nguồn]
Đa thức lượng giác là tổ hợp tuyến tính của các hàm số sin(nx) và cos(nx) với n lấy giá trị của một hay nhiều số tự nhiên.[20] Hệ số có thể là số thực hoặc là hàm số thực.
Nếu sin(nx) và cos(nx) mở rộng thành sin(x) và cos(x), đa thức lượng giác trở thành đa thức trong hai biến sin(x) và cos(x) (sử dụng các đẳng thức lượng giác). Ngược lại, mọi đa thức trong sin(x) và cos(x) đều có thể đổi lại về tổ hợp tuyến tính của các hàm sin(nx) và cos(nx). Sự tương đương giải thích ví sao cũng có thể gọi tổ hợp tuyến tính là đa thức.
Đối với hệ số phức, không có sự khác biệt giữa hàm số này với chuỗi Fourier.
Đa thức lượng giác được sử dụng rộng rãi, ví dụ như trong nội suy lượng giác áp dụng cho nội suy các hàm tuần hoàn. Chúng cũng được dùng trong biến đổi Fourier rời rạc.
Đa thức ma trận[sửa | sửa mã nguồn]
Đa thức ma trận là đa thức có các biến nhận giá trị là ma trận vuông.[21] Cho đa thức sau
kết quả đa thức tính tại ma trận A là
trong đó I là ma trận đơn vị.[22]
Các khái niệm liên quan[sửa | sửa mã nguồn]
Hàm hữu tỉ[sửa | sửa mã nguồn]
Phân thức hữu tỉ là thương (phân thức đại số) của hai đa thức. Mọi biểu thức đại số có thể viết lại thành phân thức hữu tỉ đều có thể định nghĩa hàm hữu tỉ.
Trong khi hàm đa thức nói chung xác định trên toàn miền của hàm số, hàm hữu tỉ chỉ xác định trên các giá trị các biến mà phần mẫu số khác không.
Phân thức hữu tỉ có bao gồm đa thức Laurent, nhưng không giới hạn bậc của mẫu số.
Đa thức Laurent[sửa | sửa mã nguồn]
Đa thức Laurent giống với đa thức thông thường, nhưng cho phép số mũ âm.
Chuỗi luỹ thừa[sửa | sửa mã nguồn]
Chuỗi luỹ thừa hình thức giống với đa thức, nhưng có cho phép vô hạn số các đơn thức, do đó nó không có bậc hữu hạn. Không giống như đa thức, chuỗi này không thể viết hết ra được (giống như việc không thể viết ra toàn bộ số vô tỉ), nhưng mà các quy tắc biến đổi chuỗi thì tương tự như với đa thức. Chuỗi luỹ thừa không hình thức cũng tổng quát hoá đa thức nhưng phép nhân của hai chuỗi luỹ thừa đó có thể không hội tụ.
Vành đa thức[sửa | sửa mã nguồn]
Tập tất cả các đa thức của m biến trên vành K là một vành, ký hiệu là . Vành này được gọi là vành đa thức.
Lịch sử[sửa | sửa mã nguồn]
Tìm nghiệm của đa thức, hay "giải phương trình đại số", là một trong những bài toán cổ nhất của toán học. Tuy nhiên, các phương pháp gọn và hữu ích mà ta dùng ngày nay mới chỉ bắt đầu phát triển từ thế kỷ 15. Trước thời gian đó, các phương trình thường được viết bằng lời. Lấy ví dụ như .
Xem thêm[sửa | sửa mã nguồn]
Chú thích[sửa | sửa mã nguồn]
- ^ Weisstein, Eric W. “Polynomial”. mathworld.wolfram.com (bằng tiếng Anh). Truy cập ngày 28 tháng 8 năm 2020.
- ^ a b “Polynomials | Brilliant Math & Science Wiki”. brilliant.org (bằng tiếng Anh). Truy cập ngày 28 tháng 8 năm 2020.
- ^ a b c Barbeau 2003, tr. 1–2
- ^ Weisstein, Eric W., "Zero Polynomial" từ MathWorld.
- ^ Edwards 1995, tr. 78
- ^ a b c Edwards, Harold M. (1995). Linear Algebra. Springer. tr. 47. ISBN 978-0-8176-3731-6.
- ^ Salomon, David (2006). Coding for Data and Computer Communications. Springer. tr. 459. ISBN 978-0-387-23804-3.
- ^ a b Introduction to Algebra (bằng tiếng Anh). Yale University Press. 1965. tr. 621.
Any two such polynomials can be added, subtracted, or multiplied. Furthermore , the result in each case is another polynomial
- ^ Kriete, Hartje (20 tháng 5 năm 1998). Progress in Holomorphic Dynamics (bằng tiếng Anh). CRC Press. tr. 159. ISBN 978-0-582-32388-9.
This class of endomorphisms is closed under composition,
- ^ Marecek, Lynn; Mathis, Andrea Honeycutt (6 tháng 5 năm 2020). Intermediate Algebra 2e. OpenStax. §7.1.
- ^ Haylock, Derek; Cockburn, Anne D. (14 tháng 10 năm 2008). Understanding Mathematics for Young Children: A Guide for Foundation Stage and Lower Primary Teachers (bằng tiếng Anh). SAGE. tr. 49. ISBN 978-1-4462-0497-9.
We find that the set of integers is not closed under this operation of division.
- ^ a b Marecek & Mathis 2020, §5.4]
- ^ Selby, Peter H.; Slavin, Steve (1991). Practical Algebra: A Self-Teaching Guide (ấn bản 2). Wiley. ISBN 978-0-471-53012-1.
- ^ Weisstein, Eric W. “Ruffini's Rule”. mathworld.wolfram.com (bằng tiếng Anh). Truy cập ngày 25 tháng 7 năm 2020.
- ^ Barbeau 2003, tr. 80–2
- ^ Barbeau 2003, tr. 64–5
- ^ Proskuryakov, I.V. (1994). “Algebraic equation”. Trong Hazewinkel, Michiel (biên tập). Encyclopaedia of Mathematics. 1. Springer. ISBN 978-1-55608-010-4.
- ^ Leung, Kam-tim; và đồng nghiệp (1992). Polynomials and Equations. Hong Kong University Press. tr. 134. ISBN 9789622092716.
- ^ McNamee, J.M. (2007). Numerical Methods for Roots of Polynomials, Part 1. Elsevier. ISBN 978-0-08-048947-6.
- ^ Powell, Michael J. D. (1981). Approximation Theory and Methods. Cambridge University Press. ISBN 978-0-521-29514-7.
- ^ Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2009) [1982]. Matrix Polynomials. Classics in Applied Mathematics. 58. Lancaster, PA: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-681-8. Zbl 1170.15300.
- ^ Horn & Johnson 1990, tr. 36.
- ^ The coefficient of a term may be any number from a specified set. If that set is the set of real numbers, we speak of "polynomials over the reals". Other common kinds of polynomials are polynomials with integer coefficients, polynomials with complex coefficients, and polynomials with coefficients that are integers modulo some prime number p.
- ^ This terminology dates from the time when the distinction was not clear between a polynomial and the function that it defines: a constant term and a constant polynomial define constant functions.[cần dẫn nguồn]
- ^ In fact, as a homogeneous function, it is homogeneous of every degree.[cần dẫn nguồn]
- ^ Some authors use "monomial" to mean "monic monomial". See Knapp, Anthony W. (2007). Advanced Algebra: Along with a Companion Volume Basic Algebra. Springer. tr. 457. ISBN 978-0-8176-4522-9.
- ^ This paragraph assumes that the polynomials have coefficients in a field.
Tham khảo[sửa | sửa mã nguồn]
- Barbeau, E.J. (2003). Polynomials. Springer. ISBN 978-0-387-40627-5.
- Bronstein, Manuel; và đồng nghiệp biên tập (2006). Solving Polynomial Equations: Foundations, Algorithms, and Applications. Springer. ISBN 978-3-540-27357-8.
- Cahen, Paul-Jean; Chabert, Jean-Luc (1997). Integer-Valued Polynomials. American Mathematical Society. ISBN 978-0-8218-0388-2.
- Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 , New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556. This classical book covers most of the content of this article.
- Leung, Kam-tim; và đồng nghiệp (1992). Polynomials and Equations. Hong Kong University Press. ISBN 9789622092716.
- Mayr, K. (1937). “Über die Auflösung algebraischer Gleichungssysteme durch hypergeometrische Funktionen”. Monatshefte für Mathematik und Physik. 45: 280–313. doi:10.1007/BF01707992. S2CID 197662587.
- McCoy, Neal H. (1968), Introduction To Modern Algebra, Revised Edition, Boston: Allyn and Bacon, LCCN 68015225
- Prasolov, Victor V. (2005). Polynomials. Springer. ISBN 978-3-642-04012-2.
- Sethuraman, B.A. (1997). “Polynomials”. Rings, Fields, and Vector Spaces: An Introduction to Abstract Algebra Via Geometric Constructibility. Springer. ISBN 978-0-387-94848-5.
- Toth, Gabor (2021). “Polynomial Expressions”. Elements of Mathematics. Undergraduate Texts in Mathematics. tr. 263–318. doi:10.1007/978-3-030-75051-0_6. ISBN 978-3-030-75050-3.
- Umemura, H. (2012) [1984]. “Resolution of algebraic equations by theta constants”. Trong Mumford, David (biên tập). Tata Lectures on Theta II: Jacobian theta functions and differential equations. Springer. tr. 261–. ISBN 978-0-8176-4578-6.
- von Lindemann, F. (1884). “Ueber die Auflösung der algebraischen Gleichungen durch transcendente Functionen”. Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen. 1884: 245–8.
- von Lindemann, F. (1892). “Ueber die Auflösung der algebraischen Gleichungen durch transcendente Functionen. II”. Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen. 1892: 245–8.
Liên kết ngoài[sửa | sửa mã nguồn]
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Đa thức. |
| Tra polynomial trong từ điển mở tiếng Việt Wiktionary |
- Hazewinkel, Michiel biên tập (2001), “Polynomial”, Bách khoa toàn thư Toán học, Springer, ISBN 978-1-55608-010-4
- “Euler's Investigations on the Roots of Equations”. Bản gốc lưu trữ ngày 24 tháng 9 năm 2012.









































![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)




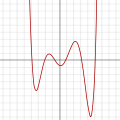








![{\displaystyle P[x_{1},x_{2},...,x_{m}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/059a12f372645aab675f1406e392c1ef7fdd11d8)