0,999...

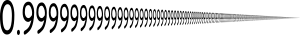
Trong toán học, số thập phân tuần hoàn '0,999... hay còn được viết $0.{\bar {9}},0,{\dot {9}}$ hoặc $0,(9)\,\!$ là một số thực bằng 1. Nói cách khác: kí hiệu 0,999... và 1 đều thể hiệu cùng một số thực. Điều này đã được nhiều giáo sư toán học trên thế giới công nhận và được giảng dạy trong nhiều sách giáo khoa. Nhiều cách chứng minh đã được trình bày với các mức độ chính xác khác nhau, dựa vào nhiều phép tính toán trên các số thực, các kiến thức được thừa nhận, bối cảnh lịch sử và mục tiêu của người đọc.

Thực tế là số thực có thực có thể được đại diện bởi một dãy số thập phân vô hạn.

The fact that certain real numbers can be represented by more than one digit string is not limited to the decimal system. The same phenomenon occurs in all integer bases, and mathematicians have also quantified the ways of writing 1 in non-integer bases. Nor is this phenomenon unique to 1: every non-zero, terminating decimal has a twin with trailing 9s, such as 28.3287 and 28.3286999…. For simplicity, the terminating decimal is almost always the preferred representation, contributing to a misconception that it is the only representation. Even more generally, any positional numeral system contains infinitely many numbers with multiple representations. These various identities have been applied to better understand patterns in the decimal expansions of fractions and the structure of a simple fractal, the Cantor set. They also occur in a classic investigation of the infinitude of the entire set of real numbers.

In the last few decades, researchers of mathematics education have studied the reception of this equality among students, many of whom initially question or reject this equality. Many are persuaded by textbooks, teachers and arithmetic reasoning as below to accept that the two are equal. However, they are often uneasy enough that they offer further justification. The students' reasoning for denying or affirming the equality is typically based on one of a few common erroneous intuitions about the real numbers; for example that each real number has a unique decimal expansion, that nonzero infinitesimal real numbers should exist, or that the expansion of 0.999… eventually terminates. Number systems that bear out some of these intuitions can be constructed, but only outside the standard real number system used in elementary, and most higher, mathematics. Indeed, some settings contain numbers that are "just shy" of 1; these are generally unrelated to 0.999…, but they are of considerable interest in mathematical analysis.

Chứng minh

Số học

Phân số và phép chia

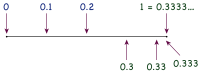
One reason that infinite decimals are a necessary extension of finite decimals is to represent fractions. Using long division, a simple division of integers like ¹⁄₃ becomes a recurring decimal, 0.333…, in which the digits repeat without end. This decimal yields a quick proof for 0.999… = 1. Multiplication of 3 times 3 produces 9 in each digit, so 3 × 0.333… equals 0.999…. And 3 × ¹⁄₃ equals 1, so 0.999… = 1.

Another form of this proof multiplies ¹/₉ = 0.111… by 9.

${\begin{aligned}0.333\dots &{}={\frac {1}{3}}\\3\times 0.333\dots &{}=3\times {\frac {1}{3}}={\frac {3\times 1}{3}}\\0.999\dots &{}=1\end{aligned}}$

${\begin{aligned}0.111\dots &{}={\frac {1}{9}}\\9\times 0.111\dots &{}=9\times {\frac {1}{9}}={\frac {9\times 1}{9}}\\0.999\dots &{}=1\end{aligned}}$

A more compact version of the same proof is given by the following equations:

$1={\frac {9}{9}}=9\times {\frac {1}{9}}=9\times 0.111\dots =0.999\dots$

Since both equations are valid, 0.999… must equal 1 (by the transitive property). Similarly, ³/_{3 = 1, and ³/3 = 0.999…. So, 0.999… must equal 1.}

Biến đổi số học

Another kind of proof more easily adapts to other repeating decimals. When a number in decimal notation is multiplied by 10, the digits do not change but the decimal separator moves one place to the right. Thus 10 × 0.999… equals 9.999…, which is 9 greater than the original number.

To see this, consider that subtracting 0.999… from 9.999… can proceed digit by digit; in each of the digits after the decimal separator the result is 9 − 9, which is 0. But trailing zeros do not change a number, so the difference is exactly 9. The final step uses algebra. Let the decimal number in question, 0.999…, be called x. Then 10x − x = 9. This is the same as 9x = 9. Dividing both sides by 9 completes the proof: x = 1. Written as a sequence of equations,

${\begin{aligned}x&=0.999\ldots \\10x&=9.999\ldots \\10x-x&=9.999\ldots -0.999\ldots \\9x&=9\\x&=1\\0.999\ldots &=1\end{aligned}}$

The validity of the digit manipulations in the above two proofs does not have to be taken on faith or as an axiom; it follows from the fundamental relationship between decimals and the numbers they represent. This relationship, which can be developed in several equivalent manners, already establishes that the decimals 0.999… and 1.000... both represent the same number.

Giải tích

Since the question of 0.999… does not affect the formal development of mathematics, it can be postponed until one proves the standard theorems of real analysis. One requirement is to characterize real numbers that can be written in decimal notation, consisting of an optional sign, a finite sequence of any number of digits forming an integer part, a decimal separator, and a sequence of digits forming a fractional part. For the purpose of discussing 0.999…, the integer part can be summarized as b₀ and one can neglect negatives, so a decimal expansion has the form

$b_{0}.b_{1}b_{2}b_{3}b_{4}b_{5}\dots$

It is vital that the fraction part, unlike the integer part, is not limited to a finite number of digits. This is a positional notation, so for example the 5 in 500 contributes ten times as much as the 5 in 50, and the 5 in 0.05 contributes one tenth as much as the 5 in 0.5.

Chuỗi vô hạn

Xem thêm thông tin: [[:Decimal representation]]

Perhaps the most common development of decimal expansions is to define them as sums of infinite series. In general:

$b_{0}.b_{1}b_{2}b_{3}b_{4}\ldots =b_{0}+b_{1}({\tfrac {1}{10}})+b_{2}({\tfrac {1}{10}})^{2}+b_{3}({\tfrac {1}{10}})^{3}+b_{4}({\tfrac {1}{10}})^{4}+\cdots .$

For 0.999… one can apply the convergence theorem concerning geometric series:

If $|r|<1$ then $ar+ar^{2}+ar^{3}+\cdots ={\frac {ar}{1-r}}.$

Since 0.999… is such a sum with a common ratio $r=\textstyle {\frac {1}{10}}$, the theorem makes short work of the question:

$0.999\ldots =9({\tfrac {1}{10}})+9({\tfrac {1}{10}})^{2}+9({\tfrac {1}{10}})^{3}+\cdots ={\frac {9({\tfrac {1}{10}})}{1-{\tfrac {1}{10}}}}=1.\,$

This proof (actually, that 10 equals 9.999…) appears as early as 1770 in Leonhard Euler's Elements of Algebra.

Limits: The unit interval, including the base-4 decimal sequence (.3, .33, .333, …) converging to 1.

The sum of a geometric series is itself a result even older than Euler. A typical 18th-century derivation used a term-by-term manipulation similar to the algebra proof given above, and as late as 1811, Bonnycastle's textbook An Introduction to Algebra uses such an argument for geometric series to justify the same maneuver on 0.999…. A 19th-century reaction against such liberal summation methods resulted in the definition that still dominates today: the sum of a series is defined to be the limit of the sequence of its partial sums. A corresponding proof of the theorem explicitly computes that sequence; it can be found in any proof-based introduction to calculus or analysis.

A sequence (x₀, x₁, x₂, …) has a limit x if the distance |x − x_n| becomes arbitrarily small as n increases. The statement that 0.999… = 1 can itself be interpreted and proven as a limit:

$0.999\ldots =\lim _{n\to \infty }0.\underbrace {99\ldots 9} _{n}=\lim _{n\to \infty }\sum _{k=1}^{n}{\frac {9}{10^{k}}}=\lim _{n\to \infty }\left(1-{\frac {1}{10^{n}}}\right)=1-\lim _{n\to \infty }{\frac {1}{10^{n}}}=1.\,$

The last step — that $\lim _{n\to \infty }{\frac {1}{10^{n}}}=0$ — is often justified by the axiom that the real numbers have the Archimedean property. This limit-based attitude towards 0.999… is often put in more evocative but less precise terms. For example, the 1846 textbook The University Arithmetic explains, ".999 +, continued to infinity = 1, because every annexation of a 9 brings the value closer to 1"; the 1895 Arithmetic for Schools says, "…when a large number of 9s is taken, the difference between 1 and .99999… becomes inconceivably small". Such heuristics are often interpreted by students as implying that 0.999… itself is less than 1.

Chia khoảng và tính bị chặn

Xem thêm thông tin: [[:Nested intervals]]

Nested intervals: in base 3, 1 = 1.000… = 0.222…

The series definition above is a simple way to define the real number named by a decimal expansion. A complementary approach is tailored to the opposite process: for a given real number, define the decimal expansion(s) to name it.

If a real number x is known to lie in the closed interval [0, 10] (i.e., it is greater than or equal to 0 and less than or equal to 10), one can imagine dividing that interval into ten pieces that overlap only at their endpoints: [0, 1], [1, 2], [2, 3], and so on up to [9, 10]. The number x must belong to one of these; if it belongs to [2, 3] then one records the digit "2" and subdivides that interval into [2, 2.1], [2.1, 2.2], …, [2.8, 2.9], [2.9, 3]. Continuing this process yields an infinite sequence of nested intervals, labeled by an infinite sequence of digits b₀, b₁, b₂, b₃, …, and one writes

x = b₀.b₁b₂b₃…

In this formalism, the identities 1 = 0.999… and 1 = 1.000… reflect, respectively, the fact that 1 lies in both [0, 1] and [1, 2], so one can choose either subinterval when finding its digits. To ensure that this notation does not abuse the "=" sign, one needs a way to reconstruct a unique real number for each decimal. This can be done with limits, but other constructions continue with the ordering theme.

One straightforward choice is the nested intervals theorem, which guarantees that given a sequence of nested, closed intervals whose lengths become arbitrarily small, the intervals contain exactly one real number in their intersection. So b₀.b₁b₂b₃… is defined to be the unique number contained within all the intervals [b₀, b₀ + 1], [b₀.b₁, b₀.b₁ + 0.1], and so on. 0.999… is then the unique real number that lies in all of the intervals [0, 1], [0.9, 1], [0.99, 1], and [0.99…9, 1] for every finite string of 9s. Since 1 is an element of each of these intervals, 0.999… = 1.

The Nested Intervals Theorem is usually founded upon a more fundamental characteristic of the real numbers: the existence of least upper bounds or suprema. To directly exploit these objects, one may define b₀.b₁b₂b₃… to be the least upper bound of the set of approximants {b₀, b₀.b₁, b₀.b₁b₂, …}. One can then show that this definition (or the nested intervals definition) is consistent with the subdivision procedure, implying 0.999… = 1 again. Tom Apostol concludes,

The fact that a real number might have two different decimal representations is merely a reflection of the fact that two different sets of real numbers can have the same supremum.

Vấn đề liên quan

• Nghịch lý Zeno

• Chia cho không

• Số âm không

Xem thêm

• Vô hạn
• Giới hạn (toán học)
• Giải tích thực
• Chuỗi (toán học)

Tham khảo

• Alligood, Sauer, and Yorke (1996). “4.1 Cantor Sets”. Chaos: An introduction to dynamical systems. Springer. ISBN 0-387-94677-2.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)

  This introductory textbook on dynamical systems is aimed at undergraduate and beginning graduate students. (p.ix)

• Apostol, Tom M. (1974). Mathematical analysis . Addison-Wesley. ISBN 0-201-00288-4.

  A transition from calculus to advanced analysis, Mathematical analysis is intended to be "honest, rigorous, up to date, and, at the same time, not too pedantic." (pref.) Apostol's development of the real numbers uses the least upper bound axiom and introduces infinite decimals two pages later. (pp.9–11)

• Bartle, R.G. and D.R. Sherbert (1982). Introduction to real analysis. Wiley. ISBN 0-471-05944-7.

  This text aims to be "an accessible, reasonably paced textbook that deals with the fundamental concepts and techniques of real analysis." Its development of the real numbers relies on the supremum axiom. (pp.vii-viii)

• Beals, Richard (2004). Analysis. Cambridge UP. ISBN 0-521-60047-2.
• Berlekamp, E.R.; J.H. Conway; and R.K. Guy (1982). Winning Ways for your Mathematical Plays. Academic Press. ISBN 0-12-091101-9.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
• Berz, Martin (1992). Automatic differentiation as nonarchimedean analysis. Elsevier. tr. 439–450.
• Bunch, Bryan H. (1982). Mathematical fallacies and paradoxes. Van Nostrand Reinhold. ISBN 0-442-24905-5.

  This book presents an analysis of paradoxes and fallacies as a tool for exploring its central topic, "the rather tenuous relationship between mathematical reality and physical reality". It assumes first-year high-school algebra; further mathematics is developed in the book, including geometric series in Chapter 2. Although 0.999… is not one of the paradoxes to be fully treated, it is briefly mentioned during a development of Cantor's diagonal method. (pp.ix-xi, 119)

• Burrell, Brian (1998). Merriam-Webster's Guide to Everyday Math: A Home and Business Reference. Merriam-Webster. ISBN 0-87779-621-1.
• Conway, John B. (1978) [1973]. Functions of one complex variable I . Springer-Verlag. ISBN 0-387-90328-3.

  This text assumes "a stiff course in basic calculus" as a prerequisite; its stated principles are to present complex analysis as "An Introduction to Mathematics" and to state the material clearly and precisely. (p.vii)

• Davies, Charles (1846). The University Arithmetic: Embracing the Science of Numbers, and Their Numerous Applications. A.S. Barnes.
• DeSua, Frank C. (1960). “A system isomorphic to the reals”. The American Mathematical Monthly. 67 (9): 900–903. doi:10.2307/2309468.
• Dubinsky, Ed, Kirk Weller, Michael McDonald, and Anne Brown (2005). “Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2”. Educational Studies in Mathematics. 60: 253–266. doi:10.1007/s10649-005-0473-0.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
• Edwards, Barbara and Michael Ward (2004). “Surprises from mathematics education research: Student (mis)use of mathematical definitions” (PDF). The American Mathematical Monthly. 111 (5): 411–425. doi:10.2307/4145268.
• Enderton, Herbert B. (1977). Elements of set theory. Elsevier. ISBN 0-12-238440-7.

  An introductory undergraduate textbook in set theory that "presupposes no specific background". It is written to accommodate a course focusing on axiomatic set theory or on the construction of number systems; the axiomatic material is marked such that it may be de-emphasized. (pp.xi-xii)

• Euler, Leonhard (1822) [1770]. John Hewlett and Francis Horner, English translators. (biên tập). Elements of Algebra (ấn bản 3). Orme Longman.
• Fjelstad, Paul (1995). “The repeating integer paradox”. The College Mathematics Journal. 26 (1): 11–15. doi:10.2307/2687285.
• Gardiner, Anthony (2003) [1982]. Understanding Infinity: The Mathematics of Infinite Processes. Dover. ISBN 0-486-42538-X.
• Gowers, Timothy (2002). Mathematics: A Very Short Introduction. Oxford UP. ISBN 0-19-285361-9.
• Grattan-Guinness, Ivor (1970). The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press. ISBN 0-262-07034-0.
• Griffiths, H.B. (1970). A Comprehensive Textbook of Classical Mathematics: A Contemporary Interpretation. London: Van Nostrand Reinhold. ISBN [[Đặc biệt:Nguồn sách/0-442-02863-6. LCC QA37.2 G75|0-442-02863-6. [[Phân loại của Thư viện Quốc hội Hoa Kỳ|LCC]]&nbsp;[https://catalog.loc.gov/vwebv/search?searchCode=CALL%2B&searchArg=QA37.2+G75&searchType=1&recCount=25 QA37.2&nbsp;G75]]].

  This book grew out of a course for Birmingham-area grammar school mathematics teachers. The course was intended to convey a university-level perspective on school mathematics, and the book is aimed at students "who have reached roughly the level of completing one year of specialist mathematical study at a university". The real numbers are constructed in Chapter 24, "perhaps the most difficult chapter in the entire book", although the authors ascribe much of the difficulty to their use of ideal theory, which is not reproduced here. (pp.vii, xiv)

• Kempner, A.J. (1936). “Anormal Systems of Numeration”. The American Mathematical Monthly. 43 (10): 610–617. doi:10.2307/2300532.
• Komornik, Vilmos; and Paola Loreti (1998). “Unique Developments in Non-Integer Bases”. The American Mathematical Monthly. 105 (7): 636–639. doi:10.2307/2589246.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
• Leavitt, W.G. (1967). “A Theorem on Repeating Decimals”. The American Mathematical Monthly. 74 (6): 669–673. doi:10.2307/2314251.
• Leavitt, W.G. (1984). “Repeating Decimals”. The College Mathematics Journal. 15 (4): 299–308. doi:10.2307/2686394.
• Lewittes, Joseph (2006). “Midy's Theorem for Periodic Decimals”. New York Number Theory Workshop on Combinatorial and Additive Number Theory. arXiv.
• Lightstone, A.H. (1972). “Infinitesimals”. The American Mathematical Monthly. 79 (3): 242–251. doi:10.2307/2316619.
• Mankiewicz, Richard (2000). The story of mathematics. Cassell. ISBN 0-304-35473-2.

  Mankiewicz seeks to represent "the history of mathematics in an accessible style" by combining visual and qualitative aspects of mathematics, mathematicians' writings, and historical sketches. (p.8)

• Maor, Eli (1987). To infinity and beyond: a cultural history of the infinite. Birkhäuser. ISBN 3-7643-3325-1.

  A topical rather than chronological review of infinity, this book is "intended for the general reader" but "told from the point of view of a mathematician". On the dilemma of rigor versus readable language, Maor comments, "I hope I have succeeded in properly addressing this problem." (pp.x-xiii)

• Mazur, Joseph (2005). Euclid in the Rainforest: Discovering Universal Truths in Logic and Math. Pearson: Pi Press. ISBN 0-13-147994-6.
• Munkres, James R. (2000) [1975]. Topology . Prentice-Hall. ISBN 0-13-181629-2.

  Intended as an introduction "at the senior or first-year graduate level" with no formal prerequisites: "I do not even assume the reader knows much set theory." (p.xi) Munkres' treatment of the reals is axiomatic; he claims of bare-hands constructions, "This way of approaching the subject takes a good deal of time and effort and is of greater logical than mathematical interest." (p.30)

• Núñez, Rafael (2006). Do Real Numbers Really Move? Language, Thought, and Gesture: The Embodied Cognitive Foundations of Mathematics. Springer. tr. 160–181. ISBN 978-0-387-25717-4.
• Pedrick, George (1994). A First Course in Analysis. Springer. ISBN 0-387-94108-8.
• Petkovšek, Marko (1990). “Ambiguous Numbers are Dense”. American Mathematical Monthly. 97 (5): 408–411. doi:10.2307/2324393.
• Pinto, Márcia and David Tall (2001). Following students' development in a traditional university analysis course (PDF). tr. v4: 57–64. Truy cập ngày 3 tháng 5 năm 2009.
• Protter, M.H. and C.B. Morrey (1991). A first course in real analysis . Springer. ISBN 0-387-97437-7.

  This book aims to "present a theoretical foundation of analysis that is suitable for students who have completed a standard course in calculus." (p.vii) At the end of Chapter 2, the authors assume as an axiom for the real numbers that bounded, nodecreasing sequences converge, later proving the nested intervals theorem and the least upper bound property. (pp.56–64) Decimal expansions appear in Appendix 3, "Expansions of real numbers in any base". (pp.503–507)

• Pugh, Charles Chapman (2001). Real mathematical analysis. Springer-Verlag. ISBN 0-387-95297-7.

  While assuming familiarity with the rational numbers, Pugh introduces Dedekind cuts as soon as possible, saying of the axiomatic treatment, "This is something of a fraud, considering that the entire structure of analysis is built on the real number system." (p.10) After proving the least upper bound property and some allied facts, cuts are not used in the rest of the book.

• Renteln, Paul and Allan Dundes (2005). “Foolproof: A Sampling of Mathematical Folk Humor” (PDF). Notices of the AMS. 52 (1): 24–34. Truy cập ngày 3 tháng 5 năm 2009.
• Richman, Fred (1999). “Is 0.999… = 1?”. Mathematics Magazine. 72 (5): 396–400. Free HTML preprint: Richman, Fred (8 tháng 6 năm 1999). “Is 0.999… = 1?”. Truy cập ngày 23 tháng 8 năm 2006. Note: the journal article contains material and wording not found in the preprint.
• Robinson, Abraham (1996). Non-standard analysis . Princeton University Press. ISBN 0-691-04490-2.
• Rosenlicht, Maxwell (1985). Introduction to Analysis. Dover. ISBN 0-486-65038-3.
• Rudin, Walter (1976) [1953]. Principles of mathematical analysis . McGraw-Hill. ISBN 0-07-054235-X.

  A textbook for an advanced undergraduate course. "Experience has convinced me that it is pedagogically unsound (though logically correct) to start off with the construction of the real numbers from the rational ones. At the beginning, most students simply fail to appreciate the need for doing this. Accordingly, the real number system is introduced as an ordered field with the least-upper-bound property, and a few interesting applications of this property are quickly made. However, Dedekind's construction is not omitted. It is now in an Appendix to Chapter 1, where it may be studied and enjoyed whenever the time is ripe." (p.ix)

• Shrader-Frechette, Maurice (1978). “Complementary Rational Numbers”. Mathematics Magazine. 51 (2): 90–98.
• Smith, Charles and Charles Harrington (1895). Arithmetic for Schools. Macmillan.
• Sohrab, Houshang (2003). Basic Real Analysis. Birkhäuser. ISBN 0-8176-4211-0.
• Stewart, Ian (1977). The Foundations of Mathematics. Oxford UP. ISBN 0-19-853165-6.
• Stewart, James (1999). Calculus: Early transcendentals . Brooks/Cole. ISBN 0-534-36298-2.

  This book aims to "assist students in discovering calculus" and "to foster conceptual understanding". (p.v) It omits proofs of the foundations of calculus.

• D.O. Tall and R.L.E. Schwarzenberger (1978). “Conflicts in the Learning of Real Numbers and Limits” (PDF). Mathematics Teaching. 82: 44–49. Truy cập ngày 3 tháng 5 năm 2009.
• Tall, David (1976/7). “Conflicts and Catastrophes in the Learning of Mathematics” (PDF). Mathematical Education for Teaching. 2 (4): 2–18. Truy cập ngày 3 tháng 5 năm 2009.
• Tall, David (2000). “Cognitive Development In Advanced Mathematics Using Technology” (PDF). Mathematics Education Research Journal. 12 (3): 210–230. Truy cập ngày 3 tháng 5 năm 2009.
• von Mangoldt, Dr. Hans (1911). “Reihenzahlen”. Einführung in die höhere Mathematik (bằng tiếng German) (ấn bản 1). Leipzig: Verlag von S. Hirzel.Quản lý CS1: ngôn ngữ không rõ (liên kết)
• Wallace, David Foster (2003). Everything and more: a compact history of infinity. Norton. ISBN 0-393-00338-8.

Liên kết ngoài

• 0,999999… = 1? từ cut-the-knot
• Tại sao 0.9999… = 1 ?
• Hỏi một nhà khoa học: Số thập phân tuần hoàn
• Phép chứng minh số học
• Chín vô hạn
• Chín vô hạn bằng một
• Nghiên cứu của David Tall về sự nhận thức toán học
• Có gì sai khi nghĩ rằng số thực là thập phân vô hạn?
• Định lý 0,999... trên Metamath
• Hackenstrings, và 0.999... ?= 1 FAQ