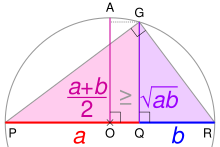
Chứng minh không cần lời của bất đẳng thức AM-GM.Chứng minh trực quan cho thấy (x + y )2 ≥ 4xy . Lấy căn bậc hai và chia cho hai ta được bất đẳng thức AM–GM.[1] Trong toán học , bất đẳng thức AM-GM là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm . Tên gọi đúng của bất đẳng thức này là bất đẳng thức trung bình cộng và trung bình nhân , nhưng thường được gọi vấn tắt là bất đẳng thức AM-GM (A rithmetic M eans - G eometric M eans). Vì có nhiều cách để chứng minh bất đẳng thức này nhưng cách chứng minh quy nạp của Cauchy được đánh giá là hiệu quả nhất nên nhiều người nhầm lẫn rằng Cauchy phát hiện ra bất đẳng thức này. Ông chỉ là người đưa ra cách chứng minh rất hay của mình chứ không phải là người phát hiện ra đầu tiên. Theo cách gọi tên chung của quốc tế, bất đẳng thức Bunyakovsky có tên là bất đẳng thức Cauchy-Schwarz , còn bất đẳng thức Cauchy (phiên âm tiếng Việt: bất đẳng thức Côsi) có tên là bất đẳng thức AM-GM.
Bất đẳng thức AM-GM có thể được phát biểu như sau:
Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng, và trung bình cộng chỉ bằng trung bình nhân khi và chỉ khi n số đó bằng nhau.
Với 2 số thực không âm a và b:
a
+
b
2
≥
a
b
{\displaystyle {\frac {a+b}{2}}\geq {\sqrt {ab}}}
khi và chỉ khi
a
=
b
{\displaystyle a=b}
Với 3 số thực không âm a, b và c:
a
+
b
+
c
3
≥
a
b
c
3
{\displaystyle {\frac {a+b+c}{3}}\geq {\sqrt[{3}]{abc}}}
Dấu "=" xảy ra khi và chỉ khi a = b = c
x
1
+
x
2
+
.
.
.
+
x
n
n
≥
x
1
.
x
2
.
.
.
.
.
x
n
n
{\displaystyle {\frac {x_{1}+x_{2}+...+x_{n}}{n}}\geq {\sqrt[{n}]{x_{1}.x_{2}.....x_{n}}}}
số tự nhiên lớn hơn 1Dấu "=" xảy ra khi và chỉ khi
x
1
=
x
2
=
.
.
.
=
x
n
{\displaystyle x_{1}=x_{2}=...=x_{n}\,}
Cho n số x 1 , x 2 ,..., x n 1 , α2 ,..., αn
Đặt
α
=
α
1
+
α
2
+
⋯
+
α
n
{\displaystyle \alpha =\alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}}
Bất đẳng thức trung bình cộng và trung bình nhân cũng đúng nếu hai giá trị trung bình có hệ số, như sau:
α
1
x
1
+
α
2
x
2
+
⋯
+
α
n
x
n
α
≥
x
1
α
1
x
2
α
2
⋯
x
n
α
n
α
{\displaystyle {\frac {\alpha _{1}x_{1}+\alpha _{2}x_{2}+\cdots +\alpha _{n}x_{n}}{\alpha }}\geq {\sqrt[{\alpha }]{x_{1}^{\alpha _{1}}x_{2}^{\alpha _{2}}\cdots x_{n}^{\alpha _{n}}}}}
Dấu " = " xảy ra khi và chỉ khi
x
1
=
x
2
=
⋯
=
x
n
{\displaystyle x_{1}=x_{2}=\cdots =x_{n}}
Với các loại trung bình khác : [ sửa | sửa mã nguồn ] Trung bình điều hòa ≤ trung bình nhân ≤ trung bình cộng
n
1
x
1
+
1
x
2
+
.
.
.
+
1
x
n
≤
x
1
x
2
.
.
.
x
n
n
≤
x
1
+
x
2
+
.
.
.
+
x
n
n
{\displaystyle {\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+...+{\frac {1}{x_{n}}}}}\leq {\sqrt[{n}]{x_{1}x_{2}...x_{n}}}\leq {\frac {x_{1}+x_{2}+...+x_{n}}{n}}}
Đẳng thức khi và chỉ khi
x
1
=
x
2
=
⋯
=
x
n
{\displaystyle x_{1}=x_{2}=\cdots =x_{n}}
Cho hàm số sau:
f
(
x
,
y
,
z
)
=
x
y
+
y
z
+
z
x
3
{\displaystyle f(x,y,z)={\frac {x}{y}}+{\sqrt {\frac {y}{z}}}+{\sqrt[{3}]{\frac {z}{x}}}}
Với x , y và z là các số thực dương. Giả sử rằng ta phải tìm giá trị nhỏ nhất của hàm số đã cho. Biến đổi và áp dụng bất đẳng thức Cauchy ta có:
f
(
x
,
y
,
z
)
{\displaystyle f(x,y,z)\,\;}
=
6
⋅
x
y
+
1
2
y
z
+
1
2
y
z
+
1
3
z
x
3
+
1
3
z
x
3
+
1
3
z
x
3
6
{\displaystyle =6\cdot {\frac {{\frac {x}{y}}+{\frac {1}{2}}{\sqrt {\frac {y}{z}}}+{\frac {1}{2}}{\sqrt {\frac {y}{z}}}+{\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}+{\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}+{\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}}{6}}}
≥
6
⋅
x
y
⋅
1
2
y
z
⋅
1
2
y
z
⋅
1
3
z
x
3
⋅
1
3
z
x
3
⋅
1
3
z
x
3
6
{\displaystyle \geq 6\cdot {\sqrt[{6}]{{\frac {x}{y}}\cdot {\frac {1}{2}}{\sqrt {\frac {y}{z}}}\cdot {\frac {1}{2}}{\sqrt {\frac {y}{z}}}\cdot {\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}\cdot {\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}\cdot {\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}}}}
=
6
⋅
1
2
⋅
2
⋅
3
⋅
3
⋅
3
x
y
y
z
z
x
6
{\displaystyle =6\cdot {\sqrt[{6}]{{\frac {1}{2\cdot 2\cdot 3\cdot 3\cdot 3}}{\frac {x}{y}}{\frac {y}{z}}{\frac {z}{x}}}}}
=
2
2
/
3
⋅
3
1
/
2
{\displaystyle =2^{2/3}\cdot 3^{1/2}}
Vậy ta có giá trị nhỏ nhất của:
f
(
x
,
y
,
z
)
là
2
2
/
3
⋅
3
1
/
2
khi
x
y
=
1
2
y
z
=
1
3
z
x
3
.
{\displaystyle f(x,y,z){\mbox{là}}2^{2/3}\cdot 3^{1/2}\quad {\mbox{khi}}\quad {\frac {x}{y}}={\frac {1}{2}}{\sqrt {\frac {y}{z}}}={\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}.}
Đặt:
μ
=
x
1
+
⋯
+
x
n
n
{\displaystyle \mu ={\frac {\ x_{1}+\cdots +x_{n}}{n}}}
bất đẳng thức tương đương vớix 1 ,...,xn là các số thực không âm, ta có:
μ
n
≥
x
1
x
2
⋯
x
n
{\displaystyle \mu ^{n}\geq x_{1}x_{2}\cdots x_{n}\,}
dấu bằng xảy ra nếu μ = xi với mọi i = 1,...,n .
Chứng minh dưới đây áp dụng phương pháp quy nạp toán học .
Cơ sở : với n = 1 bất đẳng thức đúng.
Giả thiết quy nạp: giả sử rằng bất đẳng thức đúng với n (n ≥ 1).
Quy nạp: xét n + 1 một số thực không âm. Ta có:
(
n
+
1
)
μ
=
x
1
+
⋯
+
x
n
+
x
n
+
1
.
{\displaystyle (n+1)\mu =\ x_{1}+\cdots +x_{n}+x_{n+1}.\,}
Nếu tất cả các số đều bằng μ , thì ta có đẳng thức và đã được chứng minh. Ngược lại, ta sẽ tìm được ít nhất một số nhỏ hơn μ và một số lớn hơn μ , không mất tính tổng quát, xem rằng: xn > μ và x n +1μ . Ta có:
(
x
n
−
μ
)
(
μ
−
x
n
+
1
)
>
0
.
(
∗
)
{\displaystyle (x_{n}-\mu )(\mu -x_{n+1})>0\,.\qquad (*)}
Xét n số sau:
x
1
,
…
,
x
n
−
1
,
x
n
′
{\displaystyle x_{1},\ldots ,x_{n-1},x_{n}'}
x
n
′
=
x
n
+
x
n
+
1
−
μ
≥
x
n
−
μ
>
0
,
{\displaystyle x_{n}'=x_{n}+x_{n+1}-\mu \geq x_{n}-\mu >0\,,}
cũng là số không âm. Từ đó:
n
μ
=
x
1
+
⋯
+
x
n
−
1
+
x
n
+
x
n
+
1
−
μ
⏟
=
x
n
′
,
{\displaystyle n\mu =x_{1}+\cdots +x_{n-1}+\underbrace {x_{n}+x_{n+1}-\mu } _{=\,x_{n}'},}
μ cũng là trung bình cộng của
x
1
,
…
,
x
n
−
1
,
x
n
′
{\displaystyle x_{1},\ldots ,x_{n-1},x_{n}'}
μ
n
+
1
=
μ
n
⋅
μ
≥
x
1
x
2
⋯
x
n
−
1
x
n
′
μ
.
(
∗
∗
)
{\displaystyle \mu ^{n+1}=\mu ^{n}\cdot \mu \geq x_{1}x_{2}\cdots x_{n-1}x_{n}'\mu .\qquad (**)}
Mặt khác từ (*) ta có:
(
x
n
+
x
n
+
1
−
μ
⏟
=
x
n
′
)
μ
−
x
n
x
n
+
1
=
(
x
n
−
μ
)
(
μ
−
x
n
+
1
)
>
0
,
{\displaystyle (\underbrace {x_{n}+x_{n+1}-\mu } _{=\,x_{n}'})\mu -x_{n}x_{n+1}=(x_{n}-\mu )(\mu -x_{n+1})>0,}
hay là
x
n
′
μ
>
x
n
x
n
+
1
,
(
∗
∗
∗
)
{\displaystyle x_{n}'\mu >x_{n}x_{n+1}\,,\qquad ({*}{*}{*})}
hiển nhiên μ > 0. Nếu có ít nhất một trong x 1 ,...,x n −1
μ
n
+
1
>
x
1
x
2
⋯
x
n
−
1
x
n
x
n
+
1
,
{\displaystyle \mu ^{n+1}>x_{1}x_{2}\cdots x_{n-1}x_{n}x_{n+1}\,,}
bất đẳng thức được chứng minh.
Chứng minh cho trường hợp không hệ số [ sửa | sửa mã nguồn ] Với mọi thực
x
1
,
x
2
≥
0
{\displaystyle x_{1},x_{2}\geq 0}
(
x
1
−
x
2
)
2
≥
0
⇔
x
1
−
2
x
1
x
2
+
x
2
≥
0
⇔
x
1
+
x
2
≥
2
x
1
x
2
⇔
x
1
+
x
2
2
≥
x
1
x
2
{\displaystyle ({\sqrt {x_{1}}}-{\sqrt {x_{2}}})^{2}\geq 0\Leftrightarrow x_{1}-2{\sqrt {x_{1}x_{2}}}+x_{2}\geq 0\Leftrightarrow x_{1}+x_{2}\geq 2{\sqrt {x_{1}x_{2}}}\Leftrightarrow {\frac {x_{1}+x_{2}}{2}}\geq {\sqrt {x_{1}x_{2}}}}
Giả sử
x
1
+
x
2
+
.
.
.
+
x
k
k
≥
x
1
x
2
.
.
.
x
k
k
{\displaystyle {\frac {x_{1}+x_{2}+...+x_{k}}{k}}\geq {\sqrt[{k}]{x_{1}x_{2}...x_{k}}}}
Ta có:
x
1
+
x
2
+
.
.
.
+
x
k
+
x
k
+
1
+
x
k
+
2
+
.
.
.
+
x
2
k
≥
k
x
1
x
2
.
.
.
x
k
k
+
k
x
k
+
1
x
k
+
2
.
.
.
x
2
k
k
(
1
)
{\displaystyle x_{1}+x_{2}+...+x_{k}+x_{k+1}+x_{k+2}+...+x_{2k}\geq k{\sqrt[{k}]{x_{1}x_{2}...x_{k}}}+k{\sqrt[{k}]{x_{k+1}x_{k+2}...x_{2k}}}(1)}
Áp dụng bất đẳng thức Côsi với trường hợp
n
=
2
{\displaystyle n=2}
k
x
1
x
2
.
.
.
x
k
k
+
k
x
k
+
1
x
k
+
2
.
.
.
x
2
k
k
≥
2
k
x
1
x
2
.
.
.
x
2
k
2
k
(
2
)
{\displaystyle k{\sqrt[{k}]{x_{1}x_{2}...x_{k}}}+k{\sqrt[{k}]{x_{k+1}x_{k+2}...x_{2k}}}\geq 2k{\sqrt[{2k}]{x_{1}x_{2}...x_{2k}}}(2)}
Từ
(
1
)
{\displaystyle (1)}
(
2
)
{\displaystyle (2)}
x
1
+
x
2
+
.
.
.
+
x
2
k
≥
2
k
x
1
x
2
.
.
.
x
2
k
2
k
{\displaystyle x_{1}+x_{2}+...+x_{2k}\geq 2k{\sqrt[{2k}]{x_{1}x_{2}...x_{2k}}}}
Giả sử
x
1
+
x
2
+
.
.
.
+
x
k
k
≥
x
1
x
2
.
.
.
x
k
k
{\textstyle {\frac {x_{1}+x_{2}+...+x_{k}}{k}}\geq {\sqrt[{k}]{x_{1}x_{2}...x_{k}}}}
Ta có:
x
1
+
x
2
+
.
.
.
+
x
k
+
x
k
+
1
+
x
k
+
2
.
.
.
+
x
2
k
−
1
+
x
1
x
2
.
.
.
x
2
k
−
1
2
k
−
1
≥
k
x
1
x
2
.
.
.
x
k
k
+
k
x
k
+
1
x
k
+
2
.
.
.
x
2
k
−
1
x
1
x
2
.
.
.
x
2
k
−
1
2
k
−
1
k
(
3
)
{\displaystyle x_{1}+x_{2}+...+x_{k}+x_{k+1}+x_{k+2}...+x_{2k-1}+{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}\geq k{\sqrt[{k}]{x_{1}x_{2}...x_{k}}}+k{\sqrt[{k}]{x_{k+1}x_{k+2}...x_{2k-1}{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}}}(3)}
Áp dụng bất đẳng thức Cauchy với trường hợp
n
=
2
{\displaystyle n=2}
k
x
1
x
2
.
.
.
x
k
k
+
k
x
k
+
1
x
k
+
2
.
.
.
x
1
x
2
.
.
.
x
2
k
−
1
2
k
−
1
k
≥
2
k
x
1
x
2
.
.
.
x
2
k
−
1
x
1
x
2
.
.
.
x
2
k
−
1
2
k
−
1
2
k
=
2
k
x
1
x
2
.
.
.
x
2
k
−
1
2
k
−
1
(
4
)
{\displaystyle k{\sqrt[{k}]{x_{1}x_{2}...x_{k}}}+k{\sqrt[{k}]{x_{k+1}x_{k+2}...{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}}}\geq 2k{\sqrt[{2k}]{x_{1}x_{2}...x_{2k-1}{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}}}=2k{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}(4)}
Từ
(
3
)
{\displaystyle (3)}
(
4
)
{\displaystyle (4)}
x
1
+
x
2
+
.
.
.
+
x
k
+
x
k
+
1
+
.
.
.
+
x
2
k
−
1
+
x
1
x
2
.
.
.
x
2
k
−
1
2
k
−
1
≥
2
k
x
1
x
2
.
.
.
x
2
k
−
1
2
k
−
1
{\displaystyle x_{1}+x_{2}+...+x_{k}+x_{k+1}+...+x_{2k-1}+{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}\geq 2k{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}}
Cuối cùng, ta được bất đẳng thức:
x
1
+
x
2
.
.
.
+
x
2
k
−
1
≥
(
2
k
−
1
)
x
1
x
2
.
.
.
x
2
k
−
1
2
k
−
1
{\displaystyle x_{1}+x_{2}...+x_{2k-1}\geq (2k-1){\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}}
George Pólya đưa ra một chứng minh cho bất đẳng thức như sau:[2]
Gọi f (x ) = e x −1x , có đạo hàm f ' (x ) = e x −1f ' (1) = 0 và từ đó f có giá trị nhỏ nhất tại f (1) = 0. Từ đó x ≤ ex −1x .
Xét một dãy các số thực không âm
a
1
,
a
2
,
…
,
a
n
{\displaystyle a_{1},a_{2},\dots ,a_{n}}
μ . Áp dụng bất đẳng thức ở trên ta có:
a
1
μ
a
2
μ
⋯
a
n
μ
≤
e
a
1
μ
−
1
e
a
2
μ
−
1
⋯
e
a
n
μ
−
1
=
exp
(
a
1
μ
−
1
+
a
2
μ
−
1
+
⋯
+
a
n
μ
−
1
)
.
(
1
)
{\displaystyle {{\frac {a_{1}}{\mu }}{\frac {a_{2}}{\mu }}\cdots {\frac {a_{n}}{\mu }}}\leq {e^{{\frac {a_{1}}{\mu }}-1}e^{{\frac {a_{2}}{\mu }}-1}\cdots e^{{\frac {a_{n}}{\mu }}-1}}=\exp \left({\frac {a_{1}}{\mu }}-1+{\frac {a_{2}}{\mu }}-1+\cdots +{\frac {a_{n}}{\mu }}-1\right).\qquad (1)}
Nhưng số mũ có thể rút gọn thành:
a
1
μ
−
1
+
a
2
μ
−
1
+
⋯
+
a
n
μ
−
1
=
(
a
1
+
a
2
+
⋯
+
a
n
)
μ
−
n
=
n
−
n
=
0.
{\displaystyle {\frac {a_{1}}{\mu }}-1+{\frac {a_{2}}{\mu }}-1+\cdots +{\frac {a_{n}}{\mu }}-1={\frac {(a_{1}+a_{2}+\cdots +a_{n})}{\mu }}-n=n-n=0.}
Trở lại (1),
a
1
a
2
⋯
a
n
μ
n
≤
e
0
=
1
{\displaystyle {\frac {a_{1}a_{2}\cdots a_{n}}{\mu ^{n}}}\leq e^{0}=1}
và tương đương với:
a
1
a
2
⋯
a
n
≤
μ
n
⟹
a
1
a
2
⋯
a
n
n
≤
μ
.
{\displaystyle a_{1}a_{2}\cdots a_{n}\leq \mu ^{n}\implies {\sqrt[{n}]{a_{1}a_{2}\cdots a_{n}}}\leq \mu .}
Các trường hợp tất cả các giá trị bằng nhau [ sửa | sửa mã nguồn ] Nếu tất cả các giá trị bằng nhau:
x
1
=
x
2
=
⋯
=
x
n
{\displaystyle x_{1}=x_{2}=\cdots =x_{n}}
tức tổng chúng là nx 1 , do đó giá trị trung bình cộng là x 1 ; và tích các số dưới căn bậc hai là x 1 n x 1 ; vì vậy, vế một và vế hai bằng nhau, điều phải chứng minh.
Các trường hợp các giá trị không bằng nhau [ sửa | sửa mã nguồn ] Nếu tất cả các giá trị bằng nhau không bằng nhau, thì giá trị trung bình cộng lớn hơn giá trị trung bình nhân . Rõ ràng, điều này chỉ có thể xảy ra khi n > 1. Trường hợp này khá phức tạp và được chia ra nhiều trường hợp để chứng minh.
Nếu n = 2, tức có hai giá trị x 1 và x 2 , và từ giả thiết ở trên, ta có:
x
1
≠
x
2
x
1
−
x
2
≠
0
(
x
1
−
x
2
)
2
>
0
x
1
2
−
2
x
1
x
2
+
x
2
2
>
0
x
1
2
+
2
x
1
x
2
+
x
2
2
>
4
x
1
x
2
(
x
1
+
x
2
)
2
>
4
x
1
x
2
(
x
1
+
x
2
2
)
2
>
x
1
x
2
x
1
+
x
2
2
>
x
1
x
2
{\displaystyle {\begin{aligned}x_{1}&\neq x_{2}\\[3pt]x_{1}-x_{2}&\neq 0\\[3pt]\left(x_{1}-x_{2}\right)^{2}&>0\\[3pt]x_{1}^{2}-2x_{1}x_{2}+x_{2}^{2}&>0\\[3pt]x_{1}^{2}+2x_{1}x_{2}+x_{2}^{2}&>4x_{1}x_{2}\\[3pt]\left(x_{1}+x_{2}\right)^{2}&>4x_{1}x_{2}\\[3pt]{\Bigl (}{\frac {x_{1}+x_{2}}{2}}{\Bigr )}^{2}&>x_{1}x_{2}\\[3pt]{\frac {x_{1}+x_{2}}{2}}&>{\sqrt {x_{1}x_{2}}}\end{aligned}}}
Ta có điều phải chứng minh. Xem xét các trường hợp n = 2 k k là một số nguyên dương. Chúng tôi tiến hành bằng quy nạp toán học .
Trong trường hợp cơ bản, k = 1, tức n = 2, bất đẳng thức đã được chứng minh ở trên.
Khi, có một giá trị k > 1 bất kỳ, giả sử rằng bất đẳng thức đúng với n = 2k −1n = 2k
x
1
+
x
2
+
⋯
+
x
2
k
2
k
=
x
1
+
x
2
+
⋯
+
x
2
k
−
1
2
k
−
1
+
x
2
k
−
1
+
1
+
x
2
k
−
1
+
2
+
⋯
+
x
2
k
2
k
−
1
2
≥
x
1
x
2
⋯
x
2
k
−
1
2
k
−
1
+
x
2
k
−
1
+
1
x
2
k
−
1
+
2
⋯
x
2
k
2
k
−
1
2
≥
x
1
x
2
⋯
x
2
k
−
1
2
k
−
1
x
2
k
−
1
+
1
x
2
k
−
1
+
2
⋯
x
2
k
2
k
−
1
=
x
1
x
2
⋯
x
2
k
2
k
{\displaystyle {\begin{aligned}{\frac {x_{1}+x_{2}+\cdots +x_{2^{k}}}{2^{k}}}&{}={\frac {{\frac {x_{1}+x_{2}+\cdots +x_{2^{k-1}}}{2^{k-1}}}+{\frac {x_{2^{k-1}+1}+x_{2^{k-1}+2}+\cdots +x_{2^{k}}}{2^{k-1}}}}{2}}\\[7pt]&\geq {\frac {{\sqrt[{2^{k-1}}]{x_{1}x_{2}\cdots x_{2^{k-1}}}}+{\sqrt[{2^{k-1}}]{x_{2^{k-1}+1}x_{2^{k-1}+2}\cdots x_{2^{k}}}}}{2}}\\[7pt]&\geq {\sqrt {{\sqrt[{2^{k-1}}]{x_{1}x_{2}\cdots x_{2^{k-1}}}}{\sqrt[{2^{k-1}}]{x_{2^{k-1}+1}x_{2^{k-1}+2}\cdots x_{2^{k}}}}}}\\[7pt]&={\sqrt[{2^{k}}]{x_{1}x_{2}\cdots x_{2^{k}}}}\end{aligned}}}
với bất đẳng thức đầu tiên, hai bên đều bằng nhau chỉ khi cả hai điều sau đây là đúng:
x
1
=
x
2
=
⋯
=
x
2
k
−
1
{\displaystyle x_{1}=x_{2}=\cdots =x_{2^{k-1}}}
x
2
k
−
1
+
1
=
x
2
k
−
1
+
2
=
⋯
=
x
2
k
{\displaystyle x_{2^{k-1}+1}=x_{2^{k-1}+2}=\cdots =x_{2^{k}}}
(Trong trường hợp này, trung bình số học thứ nhất và trung bình nhân thứ 1 bằng x 1 , và tương tự với trung bình số học thứ hai và trung bình nhân thứ 2); và trong bất đẳng thức thứ hai, Hai bên chỉ bằng nhau nếu hai giá trị trung bình bằng nhau. Vì không phải tất cả hai k
x
1
+
x
2
+
⋯
+
x
2
k
2
k
>
x
1
x
2
⋯
x
2
k
2
k
{\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{2^{k}}}{2^{k}}}>{\sqrt[{2^{k}}]{x_{1}x_{2}\cdots x_{2^{k}}}}}
(điều phải chứng minh).
Nếu n không phải là một hàm mũ tự nhiên cơ số 2, thì nó chắc chắn là nhỏ hơn một số nào đó theo hàm mũ tự nhiên cơ số 2, vì chuỗi 2, 4, 8,..., 2k không bị chặn trên. Do đó, mà không mất tính tổng quát, với m giá trị tuân theo hàm mũ tự nhiên cơ số 2 lớn hơn n .
Vì vậy, nếu ta có n số, thì ta có thể biểu diễn giá trị trung bình cộng α, và được mở rộng như sau:
x
n
+
1
=
x
n
+
2
=
⋯
=
x
m
=
α
.
{\displaystyle x_{n+1}=x_{n+2}=\cdots =x_{m}=\alpha .}
Sau đó ta có:
⨄
α
=
x
1
+
x
2
+
⋯
+
x
n
n
=
m
n
(
x
1
+
x
2
+
⋯
+
x
n
)
m
=
x
1
+
x
2
+
⋯
+
x
n
+
m
−
n
n
(
x
1
+
x
2
+
⋯
+
x
n
)
m
=
x
1
+
x
2
+
⋯
+
x
n
+
(
m
−
n
)
α
m
=
x
1
+
x
2
+
⋯
+
x
n
+
x
n
+
1
+
⋯
+
x
m
m
>
x
1
x
2
⋯
x
n
x
n
+
1
⋯
x
m
m
=
x
1
x
2
⋯
x
n
α
m
−
n
m
,
{\displaystyle {\begin{aligned}\biguplus \alpha &={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\\[6pt]&={\frac {{\frac {m}{n}}\left(x_{1}+x_{2}+\cdots +x_{n}\right)}{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+{\frac {m-n}{n}}\left(x_{1}+x_{2}+\cdots +x_{n}\right)}{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+\left(m-n\right)\alpha }{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}+\cdots +x_{m}}{m}}\\[6pt]&>{\sqrt[{m}]{x_{1}x_{2}\cdots x_{n}x_{n+1}\cdots x_{m}}}\\[6pt]&={\sqrt[{m}]{x_{1}x_{2}\cdots x_{n}\alpha ^{m-n}}}\,,\end{aligned}}}
như vậy:
α
m
>
x
1
x
2
⋯
x
n
α
m
−
n
α
n
>
x
1
x
2
⋯
x
n
α
>
x
1
x
2
⋯
x
n
n
{\displaystyle {\begin{aligned}\alpha ^{m}&>x_{1}x_{2}\cdots x_{n}\alpha ^{m-n}\\[5pt]\alpha ^{n}&>x_{1}x_{2}\cdots x_{n}\\[5pt]\alpha &>{\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}\end{aligned}}}
Ta suy ra điều phải chứng minh.
Các hệ quả của bất đẳng thức Cauchy [ sửa | sửa mã nguồn ] Tổng của một số thực dương và nghịch đảo của nó luôn đạt giá trị tối thiểu là 2.
Hai số thực dương có tổng không đổi thì tích 2 số đó đạt giá trị lớn nhất khi 2 số đó bằng nhau.
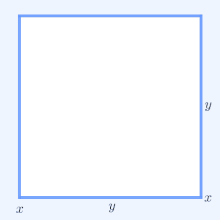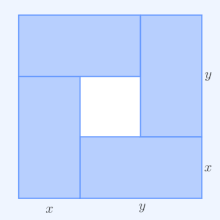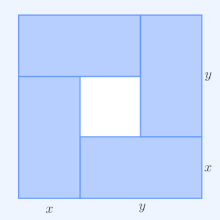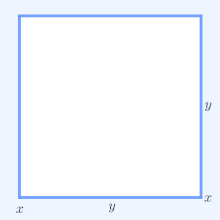
Hai số thực dương có tích không đổi thì tổng 2 số đó đạt giá trị nhỏ nhất khi 2 số đó bằng nhau. Ý nghĩa hình học của các hệ quả nêu trên [ sửa | sửa mã nguồn ] Trong các hình chữ nhật có cùng chu vi , hình vuông có diện tích lớn nhất
Trong các hình chữ nhật có cùng diện tích , hình vuông có chu vi nhỏ nhất
Việc sử dụng bất đẳng thức giúp chúng ta rất nhiều trong việc giải các phương trình vô tỉ. Ứng dụng trong Vật lý học để khảo sát công suất cực đại.



![{\displaystyle {\frac {a+b+c}{3}}\geq {\sqrt[{3}]{abc}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f2bcba0f5ef44a72f10e5f882beee94da3089e2)
![{\displaystyle {\frac {x_{1}+x_{2}+...+x_{n}}{n}}\geq {\sqrt[{n}]{x_{1}.x_{2}.....x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd6781cf75b2abc8a64a89d269c6f9e3e5eb81ff)


![{\displaystyle {\frac {\alpha _{1}x_{1}+\alpha _{2}x_{2}+\cdots +\alpha _{n}x_{n}}{\alpha }}\geq {\sqrt[{\alpha }]{x_{1}^{\alpha _{1}}x_{2}^{\alpha _{2}}\cdots x_{n}^{\alpha _{n}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a2b91d2be246172de86935612405045be57ce99)

![{\displaystyle {\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+...+{\frac {1}{x_{n}}}}}\leq {\sqrt[{n}]{x_{1}x_{2}...x_{n}}}\leq {\frac {x_{1}+x_{2}+...+x_{n}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fed87bec2e65793951229036ceefc556a456f41)
![{\displaystyle f(x,y,z)={\frac {x}{y}}+{\sqrt {\frac {y}{z}}}+{\sqrt[{3}]{\frac {z}{x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63f82a8b0a26a3c022023901ce2c13231b8a9a7e)

![{\displaystyle =6\cdot {\frac {{\frac {x}{y}}+{\frac {1}{2}}{\sqrt {\frac {y}{z}}}+{\frac {1}{2}}{\sqrt {\frac {y}{z}}}+{\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}+{\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}+{\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}}{6}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0f295c9e2335dc26a27592a449a62e4a3237c03)
![{\displaystyle \geq 6\cdot {\sqrt[{6}]{{\frac {x}{y}}\cdot {\frac {1}{2}}{\sqrt {\frac {y}{z}}}\cdot {\frac {1}{2}}{\sqrt {\frac {y}{z}}}\cdot {\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}\cdot {\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}\cdot {\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea06ac4a8acf5bcd4608a8272f76a95ae22dce2b)
![{\displaystyle =6\cdot {\sqrt[{6}]{{\frac {1}{2\cdot 2\cdot 3\cdot 3\cdot 3}}{\frac {x}{y}}{\frac {y}{z}}{\frac {z}{x}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a00ca90dd7f58d1969bbeb6d2810005b81dbcac0)

![{\displaystyle f(x,y,z){\mbox{là}}2^{2/3}\cdot 3^{1/2}\quad {\mbox{khi}}\quad {\frac {x}{y}}={\frac {1}{2}}{\sqrt {\frac {y}{z}}}={\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1fd8194da09ac7ac84eb50ffd96cf2f65124433)













![{\displaystyle {\frac {x_{1}+x_{2}+...+x_{k}}{k}}\geq {\sqrt[{k}]{x_{1}x_{2}...x_{k}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2534eb92a4c999d48f04956d02b46b61f1f699f)
![{\displaystyle x_{1}+x_{2}+...+x_{k}+x_{k+1}+x_{k+2}+...+x_{2k}\geq k{\sqrt[{k}]{x_{1}x_{2}...x_{k}}}+k{\sqrt[{k}]{x_{k+1}x_{k+2}...x_{2k}}}(1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f862b1c28335fd1228c14f221fb30323faedc8e)

![{\displaystyle k{\sqrt[{k}]{x_{1}x_{2}...x_{k}}}+k{\sqrt[{k}]{x_{k+1}x_{k+2}...x_{2k}}}\geq 2k{\sqrt[{2k}]{x_{1}x_{2}...x_{2k}}}(2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b0df47de9ce1896ade56a3955f95914774b8327)


![{\displaystyle x_{1}+x_{2}+...+x_{2k}\geq 2k{\sqrt[{2k}]{x_{1}x_{2}...x_{2k}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/696433457cc7c02f6990d29955ce392d1b76f133)
![{\textstyle {\frac {x_{1}+x_{2}+...+x_{k}}{k}}\geq {\sqrt[{k}]{x_{1}x_{2}...x_{k}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa30ffa46c4941c086971d041cd962878d149b2a)
![{\displaystyle x_{1}+x_{2}+...+x_{k}+x_{k+1}+x_{k+2}...+x_{2k-1}+{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}\geq k{\sqrt[{k}]{x_{1}x_{2}...x_{k}}}+k{\sqrt[{k}]{x_{k+1}x_{k+2}...x_{2k-1}{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}}}(3)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0feb956ab14cb4fd7810e4a84e340b01464766e)
![{\displaystyle k{\sqrt[{k}]{x_{1}x_{2}...x_{k}}}+k{\sqrt[{k}]{x_{k+1}x_{k+2}...{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}}}\geq 2k{\sqrt[{2k}]{x_{1}x_{2}...x_{2k-1}{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}}}=2k{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}(4)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/566435c09c876e0775052be40b05cd74953e06e8)


![{\displaystyle x_{1}+x_{2}+...+x_{k}+x_{k+1}+...+x_{2k-1}+{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}\geq 2k{\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/345c43084e549863d6089aa2cbec00d0da250fe0)
![{\displaystyle x_{1}+x_{2}...+x_{2k-1}\geq (2k-1){\sqrt[{2k-1}]{x_{1}x_{2}...x_{2k-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/267d2187304e981bc1369238314de4e72e535d05)




![{\displaystyle a_{1}a_{2}\cdots a_{n}\leq \mu ^{n}\implies {\sqrt[{n}]{a_{1}a_{2}\cdots a_{n}}}\leq \mu .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9cf401191a40d77b1f5e876f6421d8b27605208)
![{\displaystyle {\begin{aligned}x_{1}&\neq x_{2}\\[3pt]x_{1}-x_{2}&\neq 0\\[3pt]\left(x_{1}-x_{2}\right)^{2}&>0\\[3pt]x_{1}^{2}-2x_{1}x_{2}+x_{2}^{2}&>0\\[3pt]x_{1}^{2}+2x_{1}x_{2}+x_{2}^{2}&>4x_{1}x_{2}\\[3pt]\left(x_{1}+x_{2}\right)^{2}&>4x_{1}x_{2}\\[3pt]{\Bigl (}{\frac {x_{1}+x_{2}}{2}}{\Bigr )}^{2}&>x_{1}x_{2}\\[3pt]{\frac {x_{1}+x_{2}}{2}}&>{\sqrt {x_{1}x_{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e02b3e328bdd83f3976f7eaeb2ce2a6e91ba24c)
![{\displaystyle {\begin{aligned}{\frac {x_{1}+x_{2}+\cdots +x_{2^{k}}}{2^{k}}}&{}={\frac {{\frac {x_{1}+x_{2}+\cdots +x_{2^{k-1}}}{2^{k-1}}}+{\frac {x_{2^{k-1}+1}+x_{2^{k-1}+2}+\cdots +x_{2^{k}}}{2^{k-1}}}}{2}}\\[7pt]&\geq {\frac {{\sqrt[{2^{k-1}}]{x_{1}x_{2}\cdots x_{2^{k-1}}}}+{\sqrt[{2^{k-1}}]{x_{2^{k-1}+1}x_{2^{k-1}+2}\cdots x_{2^{k}}}}}{2}}\\[7pt]&\geq {\sqrt {{\sqrt[{2^{k-1}}]{x_{1}x_{2}\cdots x_{2^{k-1}}}}{\sqrt[{2^{k-1}}]{x_{2^{k-1}+1}x_{2^{k-1}+2}\cdots x_{2^{k}}}}}}\\[7pt]&={\sqrt[{2^{k}}]{x_{1}x_{2}\cdots x_{2^{k}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abd6928892a3005edcf7c6ef1cc3137782eecb08)


![{\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{2^{k}}}{2^{k}}}>{\sqrt[{2^{k}}]{x_{1}x_{2}\cdots x_{2^{k}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d1e238754f3dcedd3256c0d60cee9dcd27aa14a)

![{\displaystyle {\begin{aligned}\biguplus \alpha &={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\\[6pt]&={\frac {{\frac {m}{n}}\left(x_{1}+x_{2}+\cdots +x_{n}\right)}{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+{\frac {m-n}{n}}\left(x_{1}+x_{2}+\cdots +x_{n}\right)}{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+\left(m-n\right)\alpha }{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}+\cdots +x_{m}}{m}}\\[6pt]&>{\sqrt[{m}]{x_{1}x_{2}\cdots x_{n}x_{n+1}\cdots x_{m}}}\\[6pt]&={\sqrt[{m}]{x_{1}x_{2}\cdots x_{n}\alpha ^{m-n}}}\,,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/710eb6f9a9a4ad9ae3e8d581cbdf36faeaeb324a)
![{\displaystyle {\begin{aligned}\alpha ^{m}&>x_{1}x_{2}\cdots x_{n}\alpha ^{m-n}\\[5pt]\alpha ^{n}&>x_{1}x_{2}\cdots x_{n}\\[5pt]\alpha &>{\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13994bed50927b5c7b06ecf6ce5d4f9a33cdb1ae)