Bách khoa toàn thư mở Wikipedia
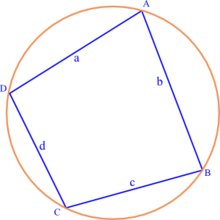
Trong hình học Euclid , công thức Brahmagupta là công thức tính diện tích của một tứ giác nội tiếp (tứ giác mà có thể vẽ một đường tròn đi qua bốn đỉnh của nó) thông qua độ dài bốn cạnh.
Nếu một tứ giác nội tiếp có độ dài các cạnh là a , b , c , d thì diện tích của nó được tính bằng công thức sau:
S
=
(
p
−
a
)
(
p
−
b
)
(
p
−
c
)
(
p
−
d
)
{\displaystyle S={\sqrt {(p-a)(p-b)(p-c)(p-d)}}}
trong đó p là nửa chu vi của tứ giác:
p
=
a
+
b
+
c
+
d
2
{\displaystyle p={\frac {a+b+c+d}{2}}}
Các công thức tương đương:
S
=
1
4
(
−
a
+
b
+
c
+
d
)
(
a
−
b
+
c
+
d
)
(
a
+
b
−
c
+
d
)
(
a
+
b
+
c
−
d
)
{\displaystyle S={\frac {1}{4}}{\sqrt {(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d)}}}
S
=
(
a
2
+
b
2
+
c
2
+
d
2
)
2
+
8
a
b
c
d
−
2
(
a
4
+
b
4
+
c
4
+
d
4
)
4
⋅
{\displaystyle S={\frac {\sqrt {(a^{2}+b^{2}+c^{2}+d^{2})^{2}+8abcd-2(a^{4}+b^{4}+c^{4}+d^{4})}}{4}}\cdot }
Diện tích tứ giác cần tìm bằng tổng diện tích hai tam giác ADB và BDC :
S
=
1
2
a
b
sin
A
+
1
2
c
d
sin
C
{\displaystyle S={\frac {1}{2}}ab\sin A+{\frac {1}{2}}cd\sin C}
Nhưng do ABCD là tứ giác nội tiếp nên hai góc A và C bù nhau (hai góc có tổng bằng 180°), suy ra
sin
A
=
sin
C
{\displaystyle \sin A=\sin C}
S
=
1
2
(
a
b
+
c
d
)
sin
A
{\displaystyle S={\frac {1}{2}}(ab+cd)\sin A}
S
2
=
1
4
(
a
b
+
c
d
)
2
sin
2
A
{\displaystyle S^{2}={\frac {1}{4}}(ab+cd)^{2}\sin ^{2}A}
4
S
2
=
(
a
b
+
c
d
)
2
(
1
−
cos
2
A
)
{\displaystyle 4S^{2}=(ab+cd)^{2}(1-\cos ^{2}A)}
4
S
2
=
(
a
b
+
c
d
)
2
−
(
a
b
+
c
d
)
2
cos
2
A
{\displaystyle 4S^{2}=(ab+cd)^{2}-(ab+cd)^{2}\cos ^{2}A}
Sử dụng định lý cos cho hai tam giác ADB và BDC với cạnh DB chung:
a
2
+
b
2
−
2
a
b
cos
A
=
c
2
+
d
2
−
2
c
d
cos
C
{\displaystyle a^{2}+b^{2}-2ab\cos A=c^{2}+d^{2}-2cd\cos C}
Thay
cos
C
=
−
cos
A
{\displaystyle \cos C=-\cos A}
A và C bù nhau):
2
(
a
b
+
c
d
)
cos
A
=
a
2
+
b
2
−
c
2
−
d
2
{\displaystyle 2(ab+cd)\cos A=a^{2}+b^{2}-c^{2}-d^{2}}
Thay vào công thức bên trên, ta có:
16
S
2
=
4
(
a
b
+
c
d
)
2
−
(
a
2
+
b
2
−
c
2
−
d
2
)
2
{\displaystyle 16S^{2}=4(ab+cd)^{2}-(a^{2}+b^{2}-c^{2}-d^{2})^{2}}
=
[
2
(
a
b
+
c
d
)
+
a
2
+
b
2
−
c
2
−
d
2
]
[
2
(
a
b
+
c
d
)
−
a
2
−
b
2
+
c
2
+
d
2
]
{\displaystyle =\left[2(ab+cd)+a^{2}+b^{2}-c^{2}-d^{2}\right]\left[2(ab+cd)-a^{2}-b^{2}+c^{2}+d^{2}\right]}
=
[
(
a
+
b
)
2
−
(
c
−
d
)
2
]
[
(
c
+
d
)
2
−
(
a
−
b
)
2
]
{\displaystyle =\left[(a+b)^{2}-(c-d)^{2}\right]\left[(c+d)^{2}-(a-b)^{2}\right]}
=
(
a
+
b
+
c
−
d
)
(
a
+
b
−
c
+
d
)
(
a
−
b
+
c
+
d
)
(
−
a
+
b
+
c
+
d
)
.
{\displaystyle =(a+b+c-d)(a+b-c+d)(a-b+c+d)(-a+b+c+d).}
Thay
a
+
b
+
c
+
d
=
2
p
{\displaystyle a+b+c+d=2p}
16
S
2
=
(
2
p
−
2
a
)
(
2
p
−
2
b
)
(
2
p
−
2
c
)
(
2
p
−
2
d
)
{\displaystyle 16S^{2}=(2p-2a)(2p-2b)(2p-2c)(2p-2d)}
hay
S
=
(
p
−
a
)
(
p
−
b
)
(
p
−
c
)
(
p
−
d
)
{\displaystyle S={\sqrt {(p-a)(p-b)(p-c)(p-d)}}}
Các nội dung liên quan, hệ quả [ sửa | sửa mã nguồn ] Công thức Heron tính diện tích tam giác có thể được suy ra từ công thức Brahmagupta nếu xem một cạnh của tứ giác, chẳng hạn, d , bằng 0 (tam giác được xem là một trường hợp đặc biệt của tứ giác nội tiếp khi một cạnh của tứ giác nội tiếp bằng không).Công thức Brahmagupta mở rộng tính diện tích một tứ giác bất kì (không nhất thiết nội tiếp) (còn được biết đến với tên gọi công thức Bretschneider ):
S
=
(
p
−
a
)
(
p
−
b
)
(
p
−
c
)
(
p
−
d
)
−
a
b
c
d
cos
2
θ
{\displaystyle S={\sqrt {(p-a)(p-b)(p-c)(p-d)-abcd\cos ^{2}\theta }}}
trong đó θ là nửa tổng hai góc đối của tứ giác. Có thể chọn hai góc đối bất kì mà không ảnh hưởng đến kết quả của công thức, bởi tổng bốn góc trong một tứ giác bất kì bằng 360°, do đó nếu nửa tổng hai góc đối này bằng θ thì nửa tổng hai góc đối còn lại sẽ bằng 180° − θ , tuy nhiên cos(180° − θ ) = −cosθ , từ đó cos2 (180° − θ ) = cos2 θ . Công thức này còn có thể được viết dưới dạng:
S
=
(
p
−
a
)
(
p
−
b
)
(
p
−
c
)
(
p
−
d
)
−
1
4
(
a
c
+
b
d
+
u
v
)
(
a
c
+
b
d
−
u
v
)
{\displaystyle S={\sqrt {(p-a)(p-b)(p-c)(p-d)-\textstyle {1 \over 4}(ac+bd+uv)(ac+bd-uv)}}}
trong đó u và v — độ dài hai đường chéo của tứ giác. (Trong tứ giác nội tiếp , uv = ac + bd theo định lý Ptolemy , công thức này trở thành công thức Brahmagupta.)















![{\displaystyle =\left[2(ab+cd)+a^{2}+b^{2}-c^{2}-d^{2}\right]\left[2(ab+cd)-a^{2}-b^{2}+c^{2}+d^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92763b8956f147f54084b331d6f3b0691a90ec42)
![{\displaystyle =\left[(a+b)^{2}-(c-d)^{2}\right]\left[(c+d)^{2}-(a-b)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e272538389a3dfef862bd968945f3c15a36b5bc5)




