Nghịch lý Olbers
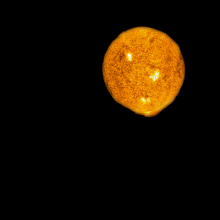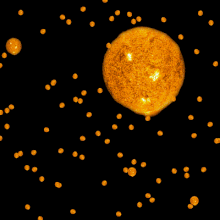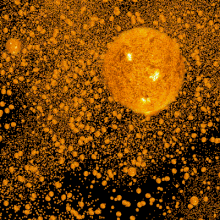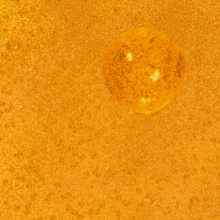
Trong vật lý thiên văn và vũ trụ học vật lý, nghịch lý Olbers, được đặt theo tên của nhà thiên văn học người Đức, Heinrich Wilhelm Olbers (1758–1840), còn được gọi là "nghịch lý bầu trời đêm tối", là lập luận rằng sự tối tăm của bầu trời đêm mâu thuẫn với giả định một vũ trụ tĩnh vô hạn và vĩnh cửu. Trong trường hợp giả định rằng vũ trụ là tĩnh, đồng nhất ở quy mô lớn và được bao phủ bởi vô số các ngôi sao, thì mọi đường ngắm từ Trái Đất phải kết thúc ở bề mặt (rất sáng) của một ngôi sao nào đó và do đó bầu trời đêm được chiếu sáng hoàn toàn và rất sáng. Điều này mâu thuẫn với sự tối tăm quan sát được và sự không đồng đều của màn đêm.[1]
Sự tối tăm của bầu trời đêm là một trong những bằng chứng cho một vũ trụ vận động, chẳng hạn như mô hình Vụ Nổ Lớn. Mô hình đó giải thích sự không đồng đều quan sát được của độ sáng bằng cách đưa vào sự giãn nở của không thời gian, kéo dài ánh sáng bắt nguồn từ Vụ Nổ Lớn đến mức bức xạ vi sóng thông qua một quá trình được gọi là dịch chuyển đỏ; bức xạ phông vi sóng này có bước sóng dài hơn nhiều so với bước sóng của ánh sáng nhìn thấy, và do đó nó trông tối tăm đối với mắt thường. Các giải thích khác cho nghịch lý đã được đưa ra, nhưng không có lời giải thích nào trong số chúng được chấp nhận rộng rãi trong giới vũ trụ học.
Lịch sử[sửa | sửa mã nguồn]
Người đầu tiên đề cập đến vấn đề vô số các ngôi sao sẽ tạo ra nhiệt lượng vô cùng lớn trong Vũ trụ là Cosmas Indicopleustes, một tu sĩ cổ Hy Lạp từ Alexandria, người khẳng định trong tác phẩm Topographia Christiana như sau: "Bầu trời được làm từ tinh thể để có thể chịu được nhiệt lượng từ Mặt Trời, Mặt Trăng, và vô tận các ngôi sao; nếu không, toàn thế gian này sẽ không gì ngoài lửa, và nó có thể thiêu cháy và làm nóng chảy bất cứ thứ gì."[2]

Cuốn Darkness at Night: A Riddle of the Universe (1987) của Edward Robert Harrison bàn về nghịch lý bầu trời đêm đen, và nó được coi là một vấn đề trong lịch sử khoa học. Theo Harrison, người đầu tiên nghĩ ra một điều tương tự như nghịch lý là Thomas Digges, cũng là người đầu tiên giải thích hệ thống vũ trụ Copernic bằng tiếng Anh và cũng mặc nhiên công nhận một vũ trụ vô hạn với vô hạn các ngôi sao.[3] Kepler cũng đặt ra vấn đề này vào năm 1610, và cuối cùng nghịch lý đã được phát biểu hoàn thiện trong công trình của Halley và Cheseaux ở thế kỷ 18.[4] Nghịch lý thường được gán cho nhà thiên văn nghiệp dư người Đức Heinrich Wilhelm Olbers, người đã mô tả nó vào năm 1823, nhưng Harrison cho thấy một cách thuyết phục rằng Olbers không phải là người đầu tiên đặt ra vấn đề này, và suy nghĩ của ông ta về nó cũng không có giá trị gì đặc biệt. Harrison lập luận rằng người đầu tiên đưa ra một giải thích thỏa đáng cho nghịch lý là Lord Kelvin, trong một bài báo ít được biết đến năm 1901,[5] và bài luận Eureka (1848) của Edgar Allan Poe đã dự đoán một cách kỳ lạ một số khía cạnh định tính trong lập luận của Kelvin:[1]
Nếu có vô hạn thế hệ các ngôi sao thì chúng ta luôn luôn được thấy nền của bầu trời thể hiện một độ sáng đều đặn, giống như sự sáng mà Dải Ngân hà trưng diện – bởi vì sẽ tuyệt nhiên không có một điểm nào ở trong toàn bộ nền trời ấy mà không tồn tại ở đó một vì sao. Vì thế, cách giải thích thỏa đáng duy nhất là dưới tình huống đó chúng ta có thể hiểu, giả định rằng tất cả những khoảng trống rỗng mà các kính viễn vọng tìm thấy xưa nay tại vô vàn các phương hướng là do cái khoảng cách tới nền trời trống vô hình quá mênh mông đến nỗi không một tia nào từ đó đã có thể tới được chúng ta.[6]
Nghịch lý[sửa | sửa mã nguồn]
Nghịch lý nêu rằng một vũ trụ tĩnh tại, vô hạn tuổi với vô hạn số các vì sao được phân bố trong một khoảng không vô cùng rộng thì sẽ trông sáng hơn là tối.[1]
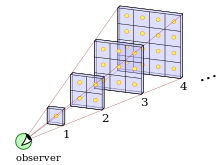
Để chỉ ra điều này, chúng ta chia vũ trụ thành một loạt các hình vỏ cầu đồng tâm, mỗi vỏ có độ dày 1 năm ánh sáng. Một số ngôi sao nhất định sẽ nằm trong lớp vỏ cách chúng ta 1.000.000.000 đến 1.000.000.001 năm ánh sáng. Nếu vũ trụ đồng nhất ở quy mô lớn, thì sẽ có số lượng sao sẽ nhiều gấp 4 lần trong lớp vỏ thứ hai, cách chúng ta từ 2.000.000.000 đến 2.000.000.000.001 năm ánh sáng. Tuy nhiên, lớp vỏ thứ hai lại ở xa gấp đôi, vì vậy mỗi ngôi sao trong đó sẽ sáng chỉ bằng một phần tư so với các ngôi sao trong lớp vỏ thứ nhất. Do đó, tổng lượng ánh sáng nhận được từ lớp vỏ thứ hai sẽ bằng với tổng lượng ánh sáng nhận được từ lớp vỏ thứ nhất.
Do đó, mỗi lớp vỏ với độ dày nhất định sẽ tạo ra lượng ánh sáng tổng như nhau bất kể nó ở khoảng cách bao xa. Có nghĩa là, lượng ánh sáng của mỗi vỏ sẽ cộng thêm vào tổng lượng ánh sáng đến ta. Như vậy với càng nhiều vỏ thì càng nhiều ánh sáng; và với vô số vỏ, thì sẽ có một bầu trời đêm sáng.
Trong khi đó nếu những đám mây tối có thể cản trở ánh sáng, những đám mây này sẽ nóng lên, cho đến khi chúng nóng như các ngôi sao, và do đó cũng tỏa ra cùng một lượng ánh sáng.
Kepler coi đây là một lập luận cho một vũ trụ quan sát được hữu hạn, hoặc ít nhất là với một số lượng hữu hạn các ngôi sao. Trong lý thuyết tương đối rộng, vẫn có thể xảy ra nghịch lý tồn tại trong một vũ trụ hữu hạn:[7] mặc dù bầu trời sẽ không sáng vô hạn, mọi điểm trên bầu trời vẫn sẽ giống như bề mặt của một ngôi sao.
Giải thích[sửa | sửa mã nguồn]
Nhà thơ Edgar Allan Poe cho rằng kích thước hữu hạn của vũ trụ quan sát được sẽ giải thích được điều nghịch lý hiển nhiên này.[8] Nói một cách cụ thể hơn, bởi vì tuổi vũ trụ chỉ hữu hạn và tốc độ ánh sáng cũng hữu hạn, cho nên chỉ có hữu hạn số các ngôi sao có thể quan sát được từ Trái Đất (dù toàn thể vũ trụ có thể vô hạn trong không gian).[9] Mật độ các sao trong thể tích hữu hạn này là đủ thấp để bất kỳ một đường ngắm nào từ Trái Đất đều không chắc chắn sẽ tới được một ngôi sao.
Tuy nhiên, lý thuyết Vụ Nổ Lớn dường như đưa ra một vấn đề mới: nó nói rằng bầu trời trong quá khứ sáng hơn nhiều, đặc biệt là vào cuối thời kỳ tái tổ hợp (recombination era), khi vũ trụ lần đầu tiên trở nên trong suốt. Tất cả các điểm của bầu trời cục bộ vào thời đại đó đều có độ sáng tương đương với bề mặt của Mặt trời, do nhiệt độ cao của vũ trụ trong thời đại đó; và hầu hết các tia sáng sẽ không bắt nguồn từ một ngôi sao mà là từ di tích của Vụ Nổ Lớn.
Vấn đề này có thể được giải quyết bởi thực tế là lý thuyết Vụ Nổ Lớn cũng gồm liên quan đến sự mở rộng không gian vũ trụ, có thể làm giảm năng lượng của ánh sáng phát ra thông qua dịch chuyển đỏ. Cụ thể hơn, bức xạ cực kỳ cao năng lượng từ Vụ Nổ Lớn đã bị dịch chuyển đỏ sang bước sóng vi sóng (gấp 1100 lần độ dài của bước sóng ban đầu) do sự giãn nở của vũ trụ, và do đó tạo thành bức xạ phông vi sóng vũ trụ không nhìn thấy được. Điều này giải thích mật độ ánh sáng và mức năng lượng tương đối thấp hiện diện trong hầu hết bầu trời của chúng ta ngày nay bất chấp bản chất sáng trong vũ trụ được giả định của thuyết Vụ Nổ Lớn. Dịch chuyển đỏ cũng ảnh hưởng tới ánh sáng từ các ngôi sao và chuẩn tinh ở xa, nhưng sự suy giảm này là rất nhỏ, vì các thiên hà và chuẩn tinh ở xa nhất chỉ có độ dịch chuyển đỏ vào khoảng 5 đến 8,6.
Các yếu tố khác[sửa | sửa mã nguồn]
Trạng thái ổn định[sửa | sửa mã nguồn]
Giả thuyết về dịch chuyển đỏ được đưa ra trong mô hình Vụ Nổ Lớn sẽ tự nó giải thích cho sự tối của bầu trời đêm ngay cả nếu vũ trụ đã già đi vô hạn. Trong lý thuyết trạng thái ổn định (Steady state theory), vũ trụ già vô hạn và đồng nhất về thời gian lẫn không gian. Không có Vụ Nổ Lớn trong mô hình của lý thuyết này, nhưng tồn tại các ngôi sao và chuẩn tinh ở những khoảng cách tùy ý. Sự giãn nở của vũ trụ dẫn đến ánh sáng từ các sao và chuẩn tinh này dịch chuyển đỏ, vì thế tổng lượng quang thông từ bầu trời vẫn luôn là hữu hạn. Do thế mật độ bức xạ quan sát được (độ sáng bầu trời của ánh sáng nền ngoài thiên hà) có thể không phụ thuộc vào sự hữu hạn của vũ trụ. Mô tả một cách toán học, tổng mật độ năng lượng điện từ (mật độ năng lượng bức xạ) trong trạng thái cân bằng nhiệt động lực học tính từ định luật Planck là:
ví dụ: đối với nhiệt độ 2,7 K nó là 40 fJ/m3 ... 4,5×10−31 kg/m3 và với nhiệt độ khả kiến 6000 K ta có 1 J/m3 ... 1,1×10−17 kg/m3. Nhưng tổng lượng bức xạ phát ra bởi một ngôi sao (hoặc các vật thể vũ trụ khác) nhiều nhất bằng tổng năng lượng liên kết hạt nhân của các đồng vị trong ngôi sao. Đối với mật độ của vũ trụ quan sát được là khoảng 4,6×10−28 kg/m3 và tính đến độ phổ biến đã biết của các nguyên tố hóa học trong vũ trụ, mật độ năng lượng bức xạ cực đại tương ứng là 9,2×10−31 kg/m3, tức là nhiệt độ 3,2 K (khớp với giá trị quan sát được đối với nhiệt độ bức xạ quang học của Arthur Eddington[10][11]). Điều này gần với tổng mật độ năng lượng của bức xạ nền vi sóng vũ trụ (CMB) và nền neutrino vũ trụ. Lý thuyết Vụ Nổ Lớn dự đoán rằng CBR phải có mật độ năng lượng bằng mật độ năng lượng liên kết hạt nhân của heli nguyên thủy, lớn hơn nhiều so với mật độ năng lượng liên kết của các nguyên tố không nguyên thủy; vì thế nó cho kết quả tương tự. Tuy nhiên, mô hình trạng thái ổn định không tiên đoán chính xác được sự phân bố góc của nhiệt độ nền vi sóng (như mô hình ΛCDM tiêu chuẩn đã tiên đoán).[12] Tuy nhiên, các lý thuyết hấp dẫn đã hiệu chỉnh (mà không tính đến sự mở rộng metric của vũ trụ) vẫn chưa thể bị loại trừ cho đến năm 2017 bởi các quan sát CMB và BAO.[13][14]
Tuổi hữu hạn của các ngôi sao[sửa | sửa mã nguồn]
Các ngôi sao có tuổi và công suất hữu hạn, do đó điều này ngụ ý rằng mỗi ngôi sao có tác động hữu hạn đến mật độ trường ánh sáng của bầu trời. Edgar Allan Poe cho rằng ý tưởng này có thể giải quyết được nghịch lý của Olbers; một lý thuyết liên quan cũng đã được đề xuất bởi Jean-Philippe de Chéseaux. Tuy vậy các ngôi sao cũng được sinh ra liên tục cùng với việc chết đi liên tục. Chỉ cần mật độ sao trong khắp vũ trụ giữ nguyên không đổi, bất kể việc chính vũ trụ có hữu hạn hay vô hạn tuổi thì sẽ vẫn luôn có vô hạn các sao khác ở cùng hướng góc ấy, với vô hạn tổng tác động. Vì vậy tuổi hữu hạn của các sao không thể giải thích được nghịch lý.[15]
Độ sáng[sửa | sửa mã nguồn]
Giả sử rằng vũ trụ không giãn nở, và luôn có cùng mật độ sao; thì nhiệt độ của vũ trụ sẽ liên tục tăng lên khi các ngôi sao tạo ra nhiều bức xạ hơn. Cuối cùng, nó sẽ đạt tới mức nhiệt độ 3000 K (tương ứng với năng lượng photon điển hình là 0,3 eV và tần số 7,5×1013 Hz), và các photon sẽ bắt đầu bị hấp thụ bởi plasma hydro lấp đầy hầu hết vũ trụ, khiến không gian ở xa trở nên mờ đục. Mật độ bức xạ cực đại này tương ứng với khoảng 12×1017 eV/m3 = 21×10−19 kg/m3, lớn hơn nhiều so với giá trị quan sát được là 47×10−31 kg/m3.[4] Vì vậy bầu trời sẽ tối hơn khoảng 500 tỉ lần so với nó nếu như vũ trụ không giãn nở hoặc quá trẻ để tiến tới sự cân bằng nhiệt. Tuy nhiên, các quan sát gần đây đã tăng cận dưới của số các thiên hà và ngụ ý rằng sự hấp thụ tia UV của hydro và sự phát xạ lại ở miền bước sóng gần hồng ngoại (không khả kiến) cũng có một vai trò.[16]
Sự phân bố fractal của sao[sửa | sửa mã nguồn]
Một giải trình khác, không dựa trên lý thuyết Vụ Nổ Lớn, được Carl Charlier đưa ra năm 1908 và sau đó được khám phá lại bởi Benoît Mandelbrot vào năm 1974. Cả hai ông đều cho rằng nếu các ngôi sao trong vũ trụ được phân bố bằng một dạng kết cấu fractal vũ trụ phân cấp (chẳng hạn, giống như kết cấu bụi Cantor)—thì mật độ trung bình của bất kỳ vùng nào sẽ tiêu giảm khi vùng đang xét tăng rộng—sẽ không cần thiết phải dựa vào thuyết Vụ Nổ Lớn để giải thích nghịch lý của Olbers. Mô hình vũ trụ này sẽ không loại trừ một Vụ Nổ Lớn, nhưng sẽ cho phép có bầu trời đêm tối nếu như Vụ Nổ Lớn không xảy ra.
Mô tả một cách toán học, ánh sáng nhận được từ các ngôi sao được biểu diễn bằng một hàm của khoảng cách sao trong một vũ trụ fractal giả định là:
trong đó:
- r0 = khoảng cách của ngôi sao gần nhất, r0 > 0;
- r = khoảng cách có thể thay đổi đo được từ Trái đất;
- L(r) = độ sáng trung bình trên mỗi sao ở khoảng cách r,
- N(r) = số sao ở khoảng cách r.
Hàm của độ sáng từ một khoảng cách nhất định L(r)N(r) xác định lượng ánh sáng nhận được là hữu hạn hay vô hạn. Đối với bất kỳ độ sáng nào từ một khoảng cách nhất định L(r)N(r) tỉ lệ với ra, giá trị là vô hạn đối với a ≥ −1 nhưng hữu hạn đối với a < −1. Vì vậy, nếu L(r) tỉ lệ với r−2, thì là hữu hạn, N(r) phải tỉ lệ với rb, trong đó b < 1. Với b = 1, số ngôi sao ở một bán kính cho trước là tỉ lệ với bán kính ấy. Khi lấy tích phân theo bán kính, điều này dẫn đến nếu b = 1, thì tổng số ngôi sao là tỉ lệ với r2. Điều đó sẽ tương ứng với số chiều fractal bằng 2. Vì vậy số chiều fractal của vũ trụ sẽ phải nhỏ hơn 2 để cho giải thích này đúng.
Giải thích này không được chấp nhận rộng rãi trong giới vũ trụ học, bởi bằng chứng cho thấy số chiều fractal của vũ trụ tối thiểu là 2.[17][18][19] Hơn nữa, phần đông các nhà vũ trụ học đều theo nguyên lý vũ trụ học,[cần dẫn nguồn] giả định rằng vật chất ở quy mô lớn hàng tỉ năm ánh sáng được phân bố đẳng hướng. Ngược lại, vũ trụ học fractal lại cần có phân bố vật chất dị hướng ở những quy mô lớn nhất. Bức xạ phông vi sóng vũ trụ có tính dị hướng cosin.[20]
Xem thêm[sửa | sửa mã nguồn]
Tham khảo[sửa | sửa mã nguồn]
- ^ a b c Overbye, Dennis (ngày 3 tháng 8 năm 2015). “The Flip Side of Optimism About Life on Other Planets”. The New York Times. Truy cập ngày 29 tháng 10 năm 2015.
- ^ "Cosmas Indicopleustès. Topographie chrétienne, 3 vols.", Ed. Wolska–Conus, W.Paris: Cerf, 1:1968; 2:1970; 3:1973; Sources chrétiennes, Book 10, section 27, line 7 "Cosmas Indicopleustès. Topographia Christiana (4061: 002) Topographie chrétienne, 3 vols.", Ed. Wolska–Conus, W. Paris: Cerf, 1:1968; 2:1970; 3:1973; Sources chrétiennes 141, 159, 197. Book 10, section 27, line 7 (Κρυσταλλώδης ἦν ὁ οὐρανὸς ἀπὸ ὑδάτων παγείς· ἐπειδὴ δὲ ἔμελλε δέχεσθαι ἡλίου φλόγα καὶ σελήνης καὶ ἄστρων ἄπειρα πλήθη, καὶ ἦν ὅλος πυρὸς πεπληρωμένος, ἵνα μὴ οὕτως ὑπὸ τῆς θερμότητος λυθῇ ἢ φλεχθῇ ἄστρων ἄπειρα πλήθη, καὶ ἦν ὅλος πυρὸς πεπληρωμένος, ἵνα μὴ οὕτως ὑπὸ τῆς θερμότητος λυθῇ ἢ φλεχθῇ.)
- ^ Hellyer, Marcus biên tập (2008). The Scientific Revolution: The Essential Readings. Blackwell Essential Readings in History. 7. John Wiley & Sons. tr. 63. ISBN 9780470754771.
The Puritan Thomas Digges (1546–1595?) was the earliest Englishman to offer a defense of the Copernican theory.... Accompanying Digges's account is a diagram of the universe portraying the heliocentric system surrounded by the orb of fixed stars, described by Digges as infinitely extended in all dimensions.
- ^ a b Unsöld, Albrecht; Baschek, Bodo (2001). The New Cosmos: An Introduction to Astronomy and Astrophysics. Physics and astronomy online. Springer. tr. 485. Bibcode:2001ncia.book.....U. ISBN 9783540678779.
The simple observation that the night sky is dark allows far-reaching conclusions to be drawn about the large-scale structure of the universe. This was already realized by J. Kepler (1610), E. Halley (1720), J.-P. Loy de Chesaux (1744), and H. W. M. Olbers (1826).
- ^ For a key extract from this paper, see Harrison (1987), pp. 227–28.
- ^ Poe, Edgar Allan (1848). “Eureka: A Prose Poem”. Bản gốc lưu trữ ngày 26 tháng 4 năm 2008. Truy cập ngày 27 tháng 11 năm 2020. Đã định rõ hơn một tham số trong
|archiveurl=và|archive-url=(trợ giúp); Đã định rõ hơn một tham số trong|archivedate=và|archive-date=(trợ giúp) - ^ D'Inverno, Ray. Introducing Einstein's Relativity, Oxford, 1992.
- ^ “Poe: Eureka”. Xroads.virginia.edu. Truy cập ngày 9 tháng 5 năm 2013.
- ^ http://www.cfa.harvard.edu/seuforum/faq.htm – Brief Answers to Cosmic Questions
- ^ Wright, Edward L. (23 tháng 10 năm 2006). “Eddington's Temperature of Space”. Truy cập ngày 10 tháng 7 năm 2013.
- ^ Eddington, A.S. (1926). Eddington's 3.18°K "Temperature of Interstellar Space". The Internal Constitution of the Stars. Cambridge University Press. tr. 371–372. Truy cập ngày 10 tháng 7 năm 2013.
- ^ Wright, E. L., E. L. “Errors in the Steady State and Quasi-SS Models”. UCLA, Physics and Astronomy Department. Truy cập ngày 28 tháng 5 năm 2015.
- ^ arXiv:1406.0485 - The observational status of Galileon gravity after Planck
- ^ arXiv:1707.02263 - Galileon Gravity in Light of ISW, CMB, BAO and H0 data
- ^ Kidger, Mark (2008), “The Mortality of the Stars”, Cosmological Enigmas: Pulsars, Quasars, and Other Deep-Space Questions, JHU Press, tr. 144–145, ISBN 9780801893353
- ^ Conselice, Christopher; Wilkinson, Aaron; Duncan, Kenneth; Mortlock, Alice (ngày 20 tháng 10 năm 2016). “THE EVOLUTION OF GALAXY NUMBER DENSITY AT z < 8 AND ITS IMPLICATIONS”. Astrophys. J. 830 (3): 83. arXiv:1607.03909. Bibcode:2016ApJ...830...83C. doi:10.3847/0004-637X/830/2/83.
- ^ Joyce, M.; Labini, F. S.; Gabrielli, A.; Montouri, M.; và đồng nghiệp (2005). “Basic Properties of Galaxy Clustering in the light of recent results from the Sloan Digital Sky Survey”. Astronomy and Astrophysics. 443 (11): 11–16. arXiv:astro-ph/0501583. Bibcode:2005A&A...443...11J. doi:10.1051/0004-6361:20053658.
- ^ Labini, F. S.; Vasilyev, N. L.; Pietronero, L.; Baryshev, Y. (2009). “Absence of self-averaging and of homogeneity in the large scale galaxy distribution”. Europhys. Lett. 86 (4): 49001. arXiv:0805.1132. Bibcode:2009EL.....8649001S. doi:10.1209/0295-5075/86/49001.
- ^ Hogg, David W.; Eisenstein, Daniel J.; Blanton, Michael R.; Bahcall, Neta A.; và đồng nghiệp (2005). “Cosmic homogeneity demonstrated with luminous red galaxies”. The Astrophysical Journal. 624 (1): 54–58. arXiv:astro-ph/0411197. Bibcode:2005ApJ...624...54H. doi:10.1086/429084.
- ^ Smoot G. F., Gorenstein M. V., and Muller R. A. (ngày 5 tháng 10 năm 1977). “Detection of Anisotropy in the Cosmic Blackbody Radiation” (PDF). Physical Review Letters. Lawrence Berkeley Laboratory và Space Sciences Laboratory, University of California, Berkeley. 39 (14): 898–901. Bibcode:1977PhRvL..39..898S. doi:10.1103/PhysRevLett.39.898. Truy cập ngày 15 tháng 9 năm 2013.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
Đọc thêm[sửa | sửa mã nguồn]
- Edward Robert Harrison (1987) Bóng tối ban đêm: Bí ẩn của Vũ trụ, Nhà xuất bản Đại học Harvard.
- Edward Robert Harrison (2000) Vũ trụ học: Khoa học về Vũ trụ, xuất bản lần thứ 2. Nhà xuất bản Đại học Cambridge. Chương 24.
- Wesson, Paul (1991). “Olbers' paradox and the spectral intensity of the extragalactic background light”. The Astrophysical Journal. 367: 399–406. Bibcode:1991ApJ...367..399W. doi:10.1086/169638.
Liên kết ngoài[sửa | sửa mã nguồn]
| Thư viện tài nguyên ngoại văn về Nghịch lý Olbers |
- Relativity FAQ about Olbers' paradox
- Astronomy FAQ about Olbers' paradox
- Cosmology FAQ about Olbers' paradox
- On Olber's Paradox MathPages
- Why is the sky dark? physics.org page about Olbers' paradox
- Why is it dark at night? A 60-second animation from the Perimeter Institute exploring the question with Alice and Bob in Wonderland



