Ngụy biện con bạc

Ngụy biện con bạc, hay ngụy biện của tay cá cược, ngụy biện Monte Carlo hoặc ngụy biện về thời cơ chín muồi, là niềm tin sai lầm rằng nếu một biến cố cụ thể xảy ra thường xuyên hơn bình thường trong quá khứ thì nó sẽ ít có khả năng xảy ra hơn trong tương lai (hoặc ngược lại), dù thực tế là xác suất các biến cố đó xảy ra không phụ thuộc vào quá khứ. Những biến cố có tính chất độc lập về lịch sử như vậy được gọi là biến cố độc lập về mặt thống kê. Ngụy biện này thường được liên hệ với cờ bạc. Ví dụ, một tay bạc có thể cho rằng lần tung xúc xắc tiếp theo có nhiều khả năng ra mặt sáu vì những lần tung gần nhất có tỷ lệ ra mặt sáu thấp hơn thông thường.
Tên gọi "ngụy biện Monte Carlo" bắt nguồn từ ví dụ nổi tiếng nhất về hiện tượng này, xảy ra tại Sòng bạc Monte Carlo năm 1913.[1]
Các ví dụ
[sửa | sửa mã nguồn]Tung đồng xu
[sửa | sửa mã nguồn]
Một minh hoạ cho ngụy biện con bạc là phép thử tung nhiều lần một đồng xu cân đối. Kết quả của các lần tung khác nhau là độc lập về mặt thống kê.
Xác suất tung ra mặt ngửa trong một lần tung là 1/2.
Xác suất tung ra mặt ngửa trong cả hai lần tung là 1/4.
Xác suất tung ra mặt ngửa trong cả ba lần tung là 1/8.
Nói chung, nếu Ai là biến cố tung i lần một đồng xu cân đối và đều ra mặt ngửa, thì xác suất xảy ra (Pr) của Ai là:
Nếu sau khi biến cố mặt ngửa xuất hiện 4 lần liên tiếp, lần tung tiếp theo cũng ra mặt ngửa, thì một chuỗi năm mặt ngửa sẽ được hình thành. Vì xác suất để chuỗi này xảy ra là 1/32, một người nào đó có thể tin rằng lần tung tiếp theo sẽ có nhiều khả năng ra mặt sấp hơn so với mặt ngửa. Điều này là không chính xác và là một ví dụ cho ảo tưởng người đánh bạc. Biến cố "5 mặt ngửa liên tiếp" và biến cố "4 mặt ngửa, rồi 1 mặt sấp" có khả năng xảy ra bằng nhau và bằng 1/32. Sau bốn lần tung đầu tiên đều ra mặt ngửa, xác suất để lần tung tiếp theo cũng ra mặt ngửa là:
Dù chuỗi năm mặt ngửa liên tiếp có xác suất là 1/32 = 0,03125 (chỉ lớn hơn 3% một chút), người chơi không nhận ra rằng đây là trường hợp ngay trước khi tung đồng xu đầu tiên. Sau bốn lần tung đầu tiên trong ví dụ này, kết quả không còn là ẩn số, vì vậy xác suất của chúng tại thời điểm đó bằng 1 (100%). Xác suất để một chuỗi ngửa hoặc sấp có độ dài bất kỳ tiếp tục cho ra một lần tung với chính mặt đó luôn là 0,5. Lập luận cho rằng lần tung thứ năm có nhiều khả năng ra mặt sấp hơn vì bốn lần tung trước đều ra mặt ngửa, rằng chuỗi may mắn trong quá khứ ảnh hưởng đến xác suất xảy ra trong tương lai, là cơ sở của ngụy biện.
Lý do đồng xu cân đối có xác suất 1/2
[sửa | sửa mã nguồn]Nếu một đồng xu cân đối được tung 21 lần, xác suất xảy ra biến cố 21 mặt ngửa liên tiếp là 1/2.097.152. Xác suất đồng xu đó tiếp tục ra mặt ngửa sau khi đã ra 20 lần mặt ngửa liên tiếp là 1/2.
Xét phép thử tung một đồng xu cân đối 21 lần:
- Xác suất biến cố "20 mặt ngửa rồi 1 mặt sấp" xảy ra là 0,520 × 0,5 = 0,521
- Xác suất biến cố "20 mặt ngửa rồi 1 mặt ngửa" xảy ra là 0,520 × 0,5 = 0,521
Xác suất xảy ra của cả hai biến cố "20 mặt ngửa rồi 1 mặt sấp" và "20 mặt ngửa rồi 1 mặt ngửa" đều là 1/2.097.152.
Trong phép thử này, hai biến cố "20 mặt ngửa rồi 1 mặt sấp" và "21 mặt ngửa" có xác suất xảy ra tương đương nhau, và cũng tương đương với bất kỳ biến cố nào khác trong không gian mẫu của phép thử đang xét, bằng 0,521, hay 1/2.097.152. Mệnh đề cho rằng xác suất sẽ thay đổi theo kết quả của các lần tung trước là không chính xác vì mọi biến cố trong không gian mẫu của phép thử trên đều có khả năng xảy ra như mọi kết quả khác. Theo định lý Bayes, xác suất của mỗi lần tung đơn lẻ bằng đúng xác suất của đồng xu cân đối: 1/2.
Những ví dụ khác
[sửa | sửa mã nguồn]Ngụy biện con bạc dẫn đến quan niệm sai lầm rằng những thất bại trước đó sẽ khiến xác suất thành công ở những lần thử tiếp theo tăng lên.
Đối với một con xúc xắc 16 mặt cân đối, xác suất của mỗi biến cố là 1/16 (6,25%). Nếu người chơi phải tung ra mặt 1 để thắng, xác suất để người đó tung ra mặt này ít nhất một lần trong 16 lần tung là:
Xác suất thua ở lần tung đầu tiên là 15/16 (93,75%).
Theo ảo tưởng người đánh bạc, người chơi sẽ có cơ hội thắng cao hơn sau khi đã thua một lần.
Trên thực tế, lúc này, xác suất để thắng ít nhất một lần là:
Sau khi thua ở lần tung đầu, xác suất chiến thắng của người chơi sẽ giảm đi 2,37%. Sau 5 lần thua, xác suất này chỉ còn khoảng 0,5083 (50,83%).
Xác suất để người chơi chiến thắng ít nhất một lần không những không tăng lên sau một chuỗi thua, mà còn giảm đi, vì số lần tung còn lại sẽ ít dần. Xác suất chiến thắng ở lần tung cuối cùng sẽ bằng xác suất khi chỉ tung một lần duy nhất, tương đương 1/16 (6,25%).
Nghịch đảo
[sửa | sửa mã nguồn]Nếu đồng xu có xu hướng ra mặt sấp, một tay bạc cũng có thể sẽ cho rằng mặt sấp là kết quả khả quan hơn, và nghĩ đồng xu có thể không cân đối. Kết luận hợp lý kiểu Bayes này không phải là ngụy biện. Nếu tin rằng tỷ lệ cược nghiêng về cửa "sấp" hơn, tay bạc sẽ không có lý do gì để đổi sang cửa "ngửa". Tuy nhiên, nếu đoán sự kiện sau dựa trên những sự kiện trước, người đó sẽ mắc lỗi ngụy biện.
Ngụy biện con bạc nghịch đảo, như Ian Hacking mô tả, là tình huống một tay bạc bước vào phòng, thấy một người tung một cặp xúc xắc ra hai mặt 6, rồi kết luận sai lầm rằng người đó đã tung xúc xắc khá lâu, vì nghĩ lần thử đầu tiên thì khó tung được như vậy.
Ngụy biện con bạc hồi tưởng
[sửa | sửa mã nguồn]Nhiều chuyên gia đã nghiên cứu xem liệu có tồn tại thiên kiến nào tương tự đối với các suy luận về các sự kiện chưa biết trong quá khứ dựa trên các sự kiện tiếp theo đã biết hay không, và gọi đây là "ngụy biện con bạc hồi tưởng".[2]
Một ví dụ cho ngụy biện con bạc hồi tưởng: một người quan sát thấy nhiều lần tung đồng xu ra mặt ngửa liên tiếp, và kết luận rằng có nhiều lần đồng xu ra mặt sấp ở những lần tung chưa biết trước đó.[2]
Nhiều người đã lập luận rằng các ví dụ thực tế cho ngụy biện này tồn tại trong nhiều sự kiện, chẳng hạn như nguồn gốc của vũ trụ. Trong tác phẩm Universes của mình, John Leslie lập luận: "sự hiện diện của nhiều vũ trụ có các đặc tính rất khác nhau có lẽ là lời giải thích thoả đáng nhất cho việc tồn tại ít nhất một vũ trụ có đặc tính cho phép sự sống".[3] Daniel M. Oppenheimer và Benoît Monin viết: "Nói cách khác, 'lời giải thích tốt nhất' cho một sự kiện có xác suất xảy ra thấp là nó chỉ là một trong nhiều lần thử. Đó là trực giác cốt lõi của ngụy biện con bạc nghịch đảo". Nhiều cuộc bàn luận triết học vẫn diễn ra, tranh cãi về việc liệu những lập luận như vậy có phải là ngụy biện hay không, và cho rằng sự xuất hiện của vũ trụ của chúng ta không nói lên điều gì về sự tồn tại của các vũ trụ khác hoặc những phép thử của các vũ trụ.[4][5] Ba nghiên cứu nhằm xác định sự tồn tại của ngụy biện con bạc hồi tưởng liên quan đến các sinh viên Đại học Stanford đã được tiến hành, và đều kết luận rằng con người sẽ sử dụng ngụy biện con bạc khi hồi tưởng cũng như với các sự kiện tương lai. Các tác giả của cả ba nghiên cứu kết luận rằng phát hiện của họ có "ý nghĩa về phương pháp luận" đáng kể nhưng cũng có thể có "ý nghĩa quan trọng về lý thuyết", và cần được điều tra, nghiên cứu: "để hiểu kỹ hơn về quá trình lập luận, chúng ta cần nghiên cứu cách chúng ảnh hưởng đến những dự đoán của chúng ta về tương lai, và cả những nhận thức về quá khứ."
Sinh con
[sửa | sửa mã nguồn]Năm 1796, trong Một bài tiểu luận triết học về xác suất, Pierre-Simon Laplace mô tả cách những người đàn ông tính toán khả năng có con trai: "Tôi đã thấy những người đàn ông khao khát có con trai. Họ cứ ghen tức với những bé trai sinh cùng tháng nhưng trước con họ. Vì nghĩ số con trai và con gái được sinh ra mỗi tháng là như nhau, nên họ cho rằng những đứa con trai sinh trước sẽ làm tăng khả năng những đứa trẻ sinh sau là con gái." Những người cha tương lai lo sợ rằng nếu những người xung quanh sinh ra nhiều con trai hơn, thì con họ sẽ có nhiều khả năng là con gái hơn. Bài luận này của Laplace được coi là một trong những mô tả đầu tiên về ngụy biện con bạc.[6]
Sau khi có nhiều con cùng giới, một số cha mẹ có thể sẽ tin rằng đứa con tiếp theo của họ sẽ khác giới. Dù giả thuyết Trivers – Willard dự đoán rằng giới tính khi sinh phụ thuộc vào điều kiện sống (trong điều kiện sống tốt thì sẽ có nhiều bé trai hơn, điều kiện sống kém hơn thì sẽ có nhiều bé gái hơn), xác suất sinh con của một trong hai giới vẫn được coi là gần 0,5 (50%).[7]
Sòng bạc Monte Carlo
[sửa | sửa mã nguồn]Một trong những ví dụ nổi tiếng nhất cho ngụy biện con bạc là một vòng roulette ở sòng bạc Monte Carlo ngày 18 tháng 8 năm 1913, khi quả bóng rơi vào ô đen 26 lần liên tiếp. Biến cố này có khả năng xảy ra cực kỳ thấp: nếu việc tung bóng hoàn toàn là ngẫu nhiên, xác suất để quả bóng rơi 26 lần liên tiếp vào ô đỏ hoặc đen là (18/37)26-1, tương đương khoảng 1/66.562.630. Những tay bạc không đặt cửa đen đã thua hàng triệu franc vì cho rằng chuỗi ô đen đã khiến tính ngẫu nhiên của vòng bị mất cân bằng, và sau chuỗi ô đen phải là một chuỗi ô đỏ.[1]
Không phải ví dụ
[sửa | sửa mã nguồn]Những biến cố không độc lập
[sửa | sửa mã nguồn]Ngụy biện con bạc không được áp dụng khi xác suất các biến cố khác nhau xảy ra không độc lập với nhau. Trong những trường hợp như hoán vị thống kê, xác suất của các biến cố sau có thể thay đổi dựa trên kết quả của các biến trong quá khứ.
Ví dụ, xét phép thử rút bài ra từ cỗ 52 lá, không có Joker:
Nếu một lá Át được rút ra mà không đặt lại, lần rút tiếp theo sẽ có nhiều khả năng ra quân khác hơn so với Át. Xác suất rút được một quân Át sẽ giảm từ 4/52 (7,69%) xuống còn 3/51 (5,88%), còn xác suất rút được quân khác lại tăng từ 4/52 (7,69%) lên 4/51 (7,84%). Hiệu ứng này cho phép sử dụng chiến thuật đếm bài trong blackjack và các trò tương tự.
Thiên hướng
[sửa | sửa mã nguồn]Trong các minh hoạ cho ngụy biện con bạc và nghịch đảo tương ứng, phép thử (chẳng hạn như tung đồng xu) được cho là hoàn toàn ngẫu nhiên. Trong thực tế, giả định này có thể không đúng. Ví dụ, nếu một đồng xu cân đối được tung 21 lần, xác suất xảy ra biến cố "21 mặt ngửa" là 1 trên 2.097.152. Vì xác suất này là rất nhỏ, nên nếu biến cố xảy ra, rất có thể đồng xu đó có xu hướng lật ngửa, hoặc do bị điều khiển bởi nam châm ẩn, hay các cách khác tương tự.[8] Trong trường hợp này, cách đặt cược thông minh là đặt vào cửa "mặt ngửa", vì suy luận kiểu Bayes từ bằng chứng thực nghiệm - 21 mặt ngửa liên tiếp - cho thấy rằng đồng xu có xu hướng ra mặt ngửa. Suy luận Bayes có thể được sử dụng để chỉ ra rằng khi tỷ lệ dài hạn của các kết quả khác nhau là không xác định nhưng có thể trao đổi (có nghĩa là quá trình ngẫu nhiên mà từ đó các kết quả được tạo ra có thể sai lệch nhưng đều có khả năng sai lệch theo bất kỳ hướng nào) và quá trình trước đó các quan sát chứng minh hướng có khả năng xảy ra sai lệch, kết quả xảy ra nhiều nhất trong quan sát cũng có khả năng xảy ra lại nhiều nhất.[9]
Ví dụ: nếu một đồng xu có 1% xác suất tiên nghiệm là không cân đối và đồng xu đó sẽ cho ra mặt ngửa trong 60% trường hợp, thì sau 21 lần ra mặt ngửa, xác suất không cân đối của đồng xu đó sẽ tăng lên đến khoảng 32%.
Vở kịch Rosencrantz và Guildenstern Are Dead (Tom Stoppard) có đề cập đến vấn đề này ở cảnh mở màn, khi một nhân vật liên tục tung ra mặt ngửa, còn người kia thì tìm cách giải thích.
Xác suất thay đổi
[sửa | sửa mã nguồn]Nếu các yếu tố bên ngoài được phép thay đổi xác suất của các sự kiện, thì ngụy biện con bạc có thể không đúng. Ví dụ: nếu luật chơi có thay đổi, một người chơi có thể sẽ có nhiều lợi thế hơn, dẫn đến tỉ lệ thắng được nâng lên. Tương tự như vậy, khả năng chiến thắng của một người chơi thiếu kinh nghiệm sẽ giảm nếu đối phương biết được và đánh vào điểm yếu của người đó. Đây là một ví dụ khác cho thiên hướng.
Tâm lý học
[sửa | sửa mã nguồn]Nguồn gốc
[sửa | sửa mã nguồn]
Nguỵ biện con bạc xuất phát từ niềm tin vào quy luật số nhỏ, dẫn đến niềm tin sai lầm rằng các mẫu nhỏ sẽ có thể đại diện cho toàn bộ quần thể lớn hơn. Theo ngụy biện, những sự bất thường cuối cùng sẽ phải đồng đều để có tính đại diện.[10] Amos Tversky và Daniel Kahneman là những người đầu tiên cho rằng nguỵ biện con bạc là một thiên kiến nhận thức, gây ra bởi một suy nghiệm tâm lý được gọi là suy nghiệm về tính đại diện. Suy nghiệm này chỉ ra cách mọi người đánh giá xác suất của một sự kiện thông qua đánh giá mức độ tương tự của nó với các sự kiện họ đã trải qua trước đây, và các sự kiện xung quanh hai quá trình đó giống nhau như thế nào.[11] Theo quan điểm này, "sau khi quan sát một chuỗi dài ô đỏ trên vòng roulette, hầu hết mọi người sẽ tin nhầm rằng thêm một ô đen sẽ khiến chuỗi tổng có tính đại diện hơn so với ô đỏ", người ta mong đợi rằng một chuỗi kết quả ngẫu nhiên sẽ có chung đặc tính với một chuỗi dài hơn, đặc biệt là việc cân bằng các sai lệch so với mức trung bình. Khi được yêu cầu tạo ra một chuỗi tung đồng xu trông có vẻ ngẫu nhiên, người ta có xu hướng tạo các chuỗi trong đó tỷ lệ ngửa/sấp ở bất kỳ đoạn ngắn nào đều nằm quanh mức 0.5. Hiện tượng này được gọi là thiếu nhạy cảm với kích thước mẫu.[12] Theo Kahneman và Tversky, nguyên nhân là vì mọi người tin rằng chuỗi ngẫu nhiên ngắn sẽ đại diện cho chuỗi dài hơn. Suy nghiệm về tính đại diện cũng đứng sau một hiện tượng liên quan - ảo giác phân cụm - khi mọi người coi chuỗi bất thường các sự kiện ngẫu nhiên là không ngẫu nhiên, dù thực tế là các chuỗi như vậy có nhiều khả năng xảy ra trong các mẫu nhỏ hơn họ tưởng.[13]
Ngụy biện con bạc cũng có thể được quy cho sự lầm tưởng rằng cờ bạc, hay chính ngẫu nhiên, là một quá trình công bằng, và có thể tự cân đối khi có những chuỗi bất thường. Điều này được gọi là ngụy biện về thế giới công bằng.[14] Các nhà nghiên cứu khác cho rằng niềm tin vào ngụy biện này có thể là hệ quả của niềm tin sai lầm vào vùng kiểm soát nội tại. Nếu ai đó tin rằng kỹ năng cá nhân của bản thân đã dẫn đến các kết quả ngẫu nhiên trong cờ bạc, họ sẽ dễ ngụy biện con bạc hơn vì họ từ chối tin rằng sự ngẫu nhiên mới là nhân tố quan trọng hơn khả năng của họ.[15]
Các biến thể
[sửa | sửa mã nguồn]Một số nhà nghiên cứu cho rằng có thể phân loại và định nghĩa hai loại ngụy biện con bạc: cổ điển (loại một) và loại hai.
Người ngụy biện con bạc kiểu cổ điển tin rằng một chuỗi dài kết quả A sẽ dẫn tới một hệ quả chắc chắn B.
Ngụy biện con bạc loại hai, theo định nghĩa của Gideon Keren và Charles Lewis, xảy ra khi tay bạc đánh giá thấp thời lượng quan sát cần thiết để xác định một hệ quả khả quan, chẳng hạn như quan sát một vòng roulette trong một khoảng thời gian rồi đặt vào những ô có tần suất xuất hiện lớn nhất. Đối với các sự kiện có mức độ ngẫu nhiên cao, việc tính toán xu hướng dẫn đến hệ quả khả quan đòi hỏi một lượng thời gian cực kỳ lớn, và rất khó, hoặc thậm chí không thể thực hiện được.[16]
Điểm khác biệt giữa hai biến thể: ngụy biện con bạc loại một giả định sai lầm rằng những điều kiện ngẫu nhiên như trong cờ bạc là công bằng và hoàn hảo; còn ngụy biện con bạc loại hai lại cho rằng những điều kiện này có xu hướng riêng, có thể bị phát hiện sau một khoảng thời gian nhất định.
Một biến thể khác là ngụy biện con bạc hồi tưởng. Người ngụy biện con bạc hồi tưởng cho rằng một sự kiện hiếm sẽ phải xảy ra trong một chuỗi dài hơn so với chuỗi bao hàm một sự kiện không hiếm bằng. Niềm tin rằng một chuỗi tung xúc xắc tưởng tượng sẽ dài hơn gấp ba lần khi một bộ ba con sáu xuất hiện trái ngược với khi chỉ có hai con sáu. Hiệu ứng này có thể xuất hiện trong các trường hợp riêng biệt hoặc tuần tự.
Oppenheimer và Monin đưa ra một ví dụ: Nếu nghe được tin đồn rằng một thiếu niên đã quan hệ tình dục không an toàn và có thai vào một đêm nào đó, thì người ta sẽ kết luận rằng cô ấy đã quan hệ không an toàn trong một khoảng thời gian dài. Nhưng nếu được cho biết thiếu niên đó tuy quan hệ không an toàn nhưng lại không có thai, khoảng thời gian giao hợp giả định mà họ đưa ra sẽ ngắn hơn. Kết luận này sai lầm ở điểm xác suất có thai của mỗi lần giao hợp không phụ thuộc vào số lần giao hợp trước đó.[17]
Mối quan hệ với ngụy biện bàn tay nóng
[sửa | sửa mã nguồn]Một quan điểm tâm lý học khác cho rằng ngụy biện con bạc có thể được coi là đối trọng với ngụy biện bàn tay nóng trong môn bóng rổ. Ngụy biện bàn tay nóng là khi mọi người có xu hướng cho rằng hệ quả sắp xảy đến cũng tương tự như sự kiện trước đó (được gọi là sự kiện tích cực gần), dẫn đến niềm tin rằng một cầu thủ đã ghi được nhiều bàn thắng sẽ tiếp tục ghi bàn.
Những người ngụy biện con bạc dự đoán sự kiện sắp xảy đến sẽ trái ngược với sự kiện trước đó (sự kiện tiêu cực gần), chẳng hạn như "vì vòng roulette đã rơi vào ô đen 6 lần liên tục rồi, nên lần tiếp theo sẽ là ô đỏ. Peter Ayton và Ilan Fischer giả thuyết rằng mọi người liên kết sự kiện tích cực gần với ngụy biện bàn tay nóng vì ngụy biện này liên quan đến hiệu suất của con người và do không tin rằng một vật vô tri vô giác có thể "nóng" lên.[18] Hiệu suất của con người không được coi là ngẫu nhiên, và người ta sẽ có xu hướng kéo dài chuỗi bất thường, nếu họ tin vào tính bất ngẫu nhiên của quá trình tạo ra kết quả.[19] Nếu một người ngụy biện con bạc, thì nhiều khả năng người đó cũng sẽ ngụy biện bàn tay nóng. Điều này dẫn đến quan điểm cho rằng có một cơ chế chung đứng sau cả hai loại ngụy biện.[15]
Các nhà nghiên cứu cũng phát hiện ra sự khác biệt giữa ngụy biện bàn tay nóng và ngụy biện con bạc trong quá trình ra quyết định về kinh tế. Năm 2010, Jürgen Huber, Michael Kirchler và Thomas Stöckl đã nghiên cứu những biểu hiện của hai loại ngụy biện này trên thị trường tài chính. Họ đã cho những đối tượng tham gia lựa chọn: đặt cược kết quả của một chuỗi tung đồng xu, sử dụng ý kiến chuyên gia để hỗ trợ đưa ra quyết định, hoặc chọn một giải pháp thay thế không có rủi ro, nhưng tiền thưởng sẽ ít hơn. Trong 24% trường hợp, các đối tượng đã ngụy biện bàn tay nóng, và chọn đưa ra quyết định dựa trên ý kiến chuyên gia, theo kinh nghiệm thành công của họ. Nếu vị chuyên gia đoán đúng, 78% số người tham gia sẽ sử dụng ý kiến của chuyên gia đó. Con số này giảm xuống 57% nếu vị chuyên gia đoán sai. Những người tham gia cũng thể hiện ngụy biện con bạc, và giảm dần các lựa chọn "ngửa" hoặc "sấp" nếu nhận thấy một chuỗi dài bất thường tương ứng. Thí nghiệm này đã giúp củng cố lý thuyết của Ayton và Fischer rằng mọi người thường tin vào hiệu suất của con người hơn là các quá trình có vẻ ngẫu nhiên.[20]
Sinh lý học thần kinh
[sửa | sửa mã nguồn]Dù suy nghiệm về tính đại diện và các thiên kiến nhận thức khác thường được coi là nguyên nhân gây ra ngụy biện con bạc, các nghiên cứu cũng cho thấy có thể có một nguyên nhân thần kinh. Ảnh chụp cộng hưởng từ chức năng chỉ ra rằng sau khi thua cược hoặc đánh bạc (rủi ro tổn thất), mạng lưới thuỳ đỉnh trước của não sẽ được kích hoạt, dẫn đến nhiều hành vi chấp nhận rủi ro hơn. Ngược lại, ở hạch hạnh nhân, thể đuôi và thể vân bụng, sau khi gặp rủi ro, các hoạt động lại giảm dần. Hoạt động ở hạch hạnh nhân có tương quan nghịch với ngụy biện con bạc: càng có nhiều hoạt động trong hạch hạnh nhân thì một cá nhân càng ít có khả năng ngụy biện con bạc. Những kết quả này cho thấy rằng ngụy biện con bạc phụ thuộc nhiều hơn vào vùng vỏ não trước trán, nơi chịu trách nhiệm điều hành, chú trọng kết quả, và ít hơn vào các vùng não kiểm soát việc ra quyết định dựa trên cảm tính.
Thể vân kiểm soát mong muốn tiếp tục chơi bạc hoặc đánh cược, đồng thời hỗ trợ một phương pháp học tập từ kết quả ngẫu nhiên. Cơ quan này xử lý các lỗi khi dự đoán và cả các hành vi thay đổi theo đó. Nếu thắng, hành vi tích cực sẽ được củng cố; nếu thua, hành vi đó sẽ bị điều kiện hoá để không lặp lại. Ở những người ngụy biện con bạc, phương pháp này bị suy yếu, và sau khi thua lỗ nhiều lần, họ vẫn tiếp tục chấp nhận rủi ro.[21]
Các giải pháp khả thi
[sửa | sửa mã nguồn]Ngụy biện con bạc là một loại thiên kiến nhận thức rất mạnh và rất khó khắc phục. Giáo dục về bản chất của ngẫu nhiên không phải lúc nào cũng có thể giảm bớt hoặc loại bỏ các biểu hiện của ngụy biện này. Trong một nghiên cứu của Lee Roy Beach và Richard Swensson vào năm 1967, các đối tượng được cho xem một bộ bài đã tráo gồm các thẻ chỉ dẫn có hình, rồi phải đoán xem những lá bài tiếp theo sẽ có hình gì. Nhóm thí nghiệm được cho biết về sự tồn tại và tính chất của ngụy biện con bạc, cũng như hướng dẫn rõ ràng để đoán mà không phụ thuộc vào những lá bài trước, còn nhóm đối chứng không được cung cấp thông tin này. Phản ứng của hai nhóm tương tự nhau, cho thấy rằng nhóm thử nghiệm vẫn bị phụ thuộc vào độ dài chuỗi bài đã biết. Họ kết luận rằng việc giải thích về tính ngẫu nhiên cho các đối tượng là không đủ để giảm bớt ngụy biện con bạc.[22]
Khả năng một người ngụy biện con bạc có thể giảm dần theo độ tuổi. Năm 1997, trong một nghiên cứu, Efraim Fischbein và Ditza Schnarch đã yêu cầu năm nhóm đối tượng trả lời một bảng câu hỏi. Năm nhóm đó được phân loại thành học sinh lớp 5, 7, 9, 11 và các sinh viên đại học chuyên dạy toán. Tất cả các đối tượng đều chưa từng học về xác suất thống kê. Câu hỏi được đặt ra là: "Ronni đã tung một đồng xu ba lần và đều ra mặt ngửa. Ronni sẽ tung đồng xu thêm một lần nữa. Khả năng đồng xu ra mặt ngửa lần thứ tư là bao nhiêu?" Kết quả chỉ ra rằng học sinh càng lớn, thì họ càng ít khi trả lời "nhỏ hơn khả năng ra mặt sấp". 35% học sinh lớp 5, 35% học sinh lớp 7 và 20% học sinh lớp 9 đã trả lời như trên, cho thấy ảnh hưởng của hiệu ứng sự kiện tiêu cực gần. Chỉ 10% học sinh lớp 11 và không có sinh viên đại học nào đưa ra câu trả lời này. Từ đó, Fischbein và Schnarch đưa ra giả thuyết rằng xu hướng dựa vào suy nghiệm về tính đại diện và các thiên kiến nhận thức khác của một cá nhân có thể sẽ giảm dần theo tuổi tác.[23]
Các nhà tâm lý học Gestalt Christopher Roney và Lana Trick đã đưa ra một giải pháp khả quan khác: gộp nhóm. Khi một sự kiện sắp xảy đến, chẳng hạn như tung đồng xu, được coi là thuộc một chuỗi sự kiện, người ta sẽ tự động liên kết sự kiện đó với các sự kiện diễn ra trước đó, dù sự kiện đó nằm ở đâu trong chuỗi, dẫn đến ngụy biện con bạc. Khi coi mọi sự kiện độc lập với nhau, ảnh hưởng của ngụy biện sẽ giảm mạnh.[24]
Roney và Trick nói với những người tham gia rằng họ sẽ đặt cược vào hai nhóm với sáu lần tung đồng xu hoặc hai nhóm bảy lần. Lần tung thứ tư, thứ năm và thứ sáu có kết quả giống nhau, đều là ngửa hoặc sấp. Lần tung thứ bảy sẽ được gộp với đuôi của một nhóm, hoặc đầu của nhóm tiếp theo. Các đối tượng ngụy biện con bạc mạnh nhất khi lần tung thứ bảy nằm trong nhóm đầu tiên, sau bộ ba lần tung mặt ngửa hoặc sấp. Các nhà nghiên cứu đã chỉ ra rằng các đối tượng không ngụy biện con bạc sẽ ít tự tin hơn vào khoản cược của họ và đặt cược ít lần hơn so với những người ngụy biện con bạc. Khi lần tung thứ bảy được gộp với nhóm thứ hai, và được coi là không nằm trong chuỗi bất thường, ngụy biện con bạc đã không xảy ra.
Roney và Trick lập luận rằng không nên cho người ta biết bản chất của sự ngẫu nhiên, mà nên khiến họ coi mỗi sự kiện là khởi đầu, không phải tiếp nối của các sự kiện xảy ra trước. Họ cũng nói điều này sẽ khiến người ta ngừng chơi bạc khi thua, và loại bỏ được niềm tin sai lầm rằng khả năng thắng của họ sẽ tăng lên, để tương quan với những lần thua trước.
Người dùng
[sửa | sửa mã nguồn]Các loại người dùng
[sửa | sửa mã nguồn]Trong bối cảnh thế giới thực, nhiều nghiên cứu đã phát hiện ra rằng những người ra quyết định khác nhau trong các tình huống rủi ro cao có thể sẽ phản ánh khá mạnh sự tự tương quan nghịch biến trong nhận định của mình.
Thẩm phán tị nạn chính trị
[sửa | sửa mã nguồn]Trong một nghiên cứu về sự tự tương quan tiêu cực với ngụy biện con bạc trong quyết định của các thẩm phán Tị nạn chính trị Hoa Kỳ, kết luận cho thấy rằng sau khi một thẩm phán cấp quyền tị nạn hai lần, khả năng người đó chấp thuận hồ sơ thứ ba sẽ giảm đi 5.5%.[25]
Trọng tài bóng chày
[sửa | sửa mã nguồn]
Trong môn bóng chày, mỗi phút đều có rất nhiều quyết định được đưa ra. Quyết định thường bị soi xét nhất của các trọng tài là quyết định "vùng đánh bóng". Nếu người đánh bóng không vung gậy, trọng tài sẽ phải quyết định xem đường bóng có đi qua vùng đánh bóng - thể tích nằm phía trên gôn nhà, được giới hạn bởi các mặt phẳng song song với mặt đất đi qua đầu gối và điểm giữa của thân trên - hay không. Nếu bóng không qua, cầu thủ đánh bóng sẽ không bị tính strike (đánh trượt bóng). Một nghiên cứu tổng hợp dữ liệu hơn 12.000 trận bóng chày cho thấy rằng khả năng các trọng tài quyết định strike sẽ giảm đi 1,3% nếu hai lần đánh bóng trước đó cũng là strike.[25]
Chuyên viên tín dụng
[sửa | sửa mã nguồn]Khích lệ tài chính được cho là yếu tố chính dẫn đến việc các chuyên viên tín dụng ra quyết định thiên lệch, khiến cho việc kiểm tra ảnh hưởng của ngụy biện con bạc trở nên khó khăn. Tuy nhiên, nghiên cứu cho thấy rằng khả năng chấp thuận một khoản vay của các chuyên viên tín dụng không được khích lệ tài chính sẽ thấp hơn 8% nếu họ đã chấp thuận cho khách hàng trước đó.[26]
Người chơi xổ số
[sửa | sửa mã nguồn]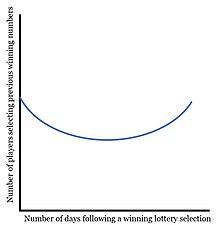
Xổ số và các loại hình tương tự thu hút rất nhiều tay bạc trên toàn cầu. Dù hầu hết những người chơi đều có chiến lược đặt cược riêng cho mình, đã có nhiều bằng chứng cho thấy rằng sau khi một mã số được công bố thắng giải, mã đó sẽ ít được chọn hơn trong những lần quay sau. Năm 1991, Charles Clotfelter và Philip Cook đã tiến hành một nghiên cứu nổi tiếng về hiệu ứng này. Họ kết luận: người chơi sẽ không đặt cược vào các mã số vừa mới thắng giải, và tỉ lệ chọn vào mã đó sẽ chỉ phổ biến trở lại sau khoảng ba tháng.[28] Ba năm sau, Dek Terrell tiến hành một nghiên cứu để kiểm tra những phát hiện của họ, nhưng có một điểm khác: mở rộng nghiên cứu sang cả loại hình xổ số cược chung. Xổ số cược chung là một con số được chọn với tổng số tiền cược càng thấp thấp hơn sẽ có kết quả trả thưởng cao hơn. Mặc dù cuộc kiểm tra này đã kết luận rằng những người chơi trong cả hai loại xổ số đều thể hiện hành vi phù hợp với lý thuyết ngụy biện của Người đánh bạc, những người tham gia cược chung dường như ít bị ảnh hưởng hơn.[27]
Bảng 1: Tỷ lệ thay đổi số của người chơi xổ số theo Clotfelter, Cook (1991)[28]
Ngụy biện con bạc đã khiến tỷ lệ chọn các mã số thắng giải giảm mạnh sau khi công bố, nhưng tăng dần lại sau khoảng hai tháng. Ví dụ, vào ngày 11 tháng 4 năm 1988, 41 người chơi đã đặt mã 244. Ba ngày sau, chỉ còn 24 người chọn mã này, giảm 41,5%. Những người chơi đã tin rằng các mã từng thắng giải sẽ có ít khả năng thắng hơn ở những lần quay sau.
| Số lần người chơi đặt | ||||||
| Mã thắng giải tuần thứ 2 tháng 4 năm 1988 | Ngày quay thưởng | Sau khi quay thưởng (ngày) | ||||
| Ngày | Mã thắng | 0 | 1 | 3 | 7 | 56 |
| 11 | 244 | 41 | 34 | 24 | 27 | 30 |
| 12 | 504 | 29 | 20 | 12 | 18 | 15 |
| 13 | 718 | 28 | 20 | 17 | 19 | 25 |
| 14 | 323 | 134 | 95 | 79 | 81 | 76 |
| 15 | 640 | 10 | 20 | 18 | 16 | 20 |
| 16 | 957 | 30 | 22 | 20 | 24 | 32 |
| Tỷ lệ số người chơi chọn mã từng trúng thưởng ở những ngày sau so với ngày quay thưởng | 78% | 63% | 68% | 73% | ||
Tham khảo
[sửa | sửa mã nguồn]- ^ a b “Why we gamble like monkeys”. BBC.com. 2 tháng 1 năm 2015.
- ^ a b Oppenheimer, D.M., & Monin, B. (2009). The retrospective gambler's fallacy: Unlikely events, constructing the past, and multiple universes. Judgment and Decision Making, vol. 4, no. 5, pp. 326-334
- ^ Leslie, J. (1989). Universes. London: Routledge.
- ^ Hacking, I (1987). “The inverse gambler's fallacy: The argument from design. The anthropic principle applied to Wheeler universes”. Mind. 96 (383): 331–340. doi:10.1093/mind/xcvi.383.331.
- ^ White, R (2000). “Fine-tuning and multiple universes”. Noûs. 34 (2): 260–276. doi:10.1111/0029-4624.00210.
- ^ Barron, Greg; Leider, Stephen (ngày 13 tháng 10 năm 2009). “The role of experience in the Gambler's Fallacy” (PDF). Journal of Behavioral Decision Making.
- ^ Palmer-Hague, Jaime (ngày 10 tháng 12 năm 2016). “Trivers-Willard hypothesis”. Encyclopedia of Evolutionary Psychological Science: 1–7. doi:10.1007/978-3-319-16999-6_1911-1. ISBN 978-3-319-16999-6 – qua SpringerLink.
- ^ Gardner, Martin (1986). Entertaining Mathematical Puzzles. Courier Dover Publications. tr. 69–70. ISBN 978-0-486-25211-7. Truy cập ngày 13 tháng 3 năm 2016.
- ^ O'Neill, B.; Puza, B.D. (2004). "Dice have no memories but I do: A defence of the reverse gambler's belief". Reprinted in abridged form as: O'Neill, B.; Puza, B.D. (2005). “In defence of the reverse gambler's belief”. The Mathematical Scientist. 30 (1): 13–16. ISSN 0312-3685.
- ^ Tversky, Amos; Daniel Kahneman (1971). “Belief in the law of small numbers” (PDF). Psychological Bulletin. 76 (2): 105–110. CiteSeerX 10.1.1.592.3838. doi:10.1037/h0031322. Bản gốc (PDF) lưu trữ ngày 24 tháng 2 năm 2021. Truy cập ngày 3 tháng 5 năm 2021.
- ^ Tversky, Amos; Daniel Kahneman (1974). “Judgment under uncertainty: Heuristics and biases”. Science. 185 (4157): 1124–1131. doi:10.1126/science.185.4157.1124. PMID 17835457. Bản gốc lưu trữ ngày 1 tháng 6 năm 2018. Truy cập ngày 3 tháng 5 năm 2021.
- ^ Tune, G. S. (1964). “Response preferences: A review of some relevant literature”. Psychological Bulletin. 61 (4): 286–302. doi:10.1037/h0048618. PMID 14140335.
- ^ Gilovich, Thomas (1991). How we know what isn't so. New York: The Free Press. tr. 16–19. ISBN 978-0-02-911706-4.
- ^ Rogers, Paul (1998). “The cognitive psychology of lottery gambling: A theoretical review”. Journal of Gambling Studies. 14 (2): 111–134. doi:10.1023/A:1023042708217. ISSN 1050-5350. PMID 12766438.
- ^ a b Sundali, J.; Croson, R. (2006). “Biases in casino betting: The hot hand and the gambler's fallacy”. Judgment and Decision Making. 1: 1–12.
- ^ Keren, Gideon; Lewis, Charles (1994). “The Two Fallacies of Gamblers: Type I and Type II”. Organizational Behavior and Human Decision Processes. 60 (1): 75–89. doi:10.1006/obhd.1994.1075. ISSN 0749-5978.
- ^ Oppenheimer, D. M.; Monin, B. (2009). “The retrospective gambler's fallacy: Unlikely events, constructing the past, and multiple universes”. Judgment and Decision Making. 4: 326–334.
- ^ Ayton, P.; Fischer, I. (2004). “The hot-hand fallacy and the gambler's fallacy: Two faces of subjective randomness?”. Memory and Cognition. 32 (8): 1369–1378. doi:10.3758/bf03206327. PMID 15900930.
- ^ Burns, Bruce D.; Corpus, Bryan (2004). “Randomness and inductions from streaks: "Gambler's fallacy" versus "hot hand"”. Psychonomic Bulletin & Review. 11 (1): 179–184. doi:10.3758/BF03206480. ISSN 1069-9384. PMID 15117006.
- ^ Huber, J.; Kirchler, M.; Stockl, T. (2010). “The hot hand belief and the gambler's fallacy in investment decisions under risk”. Theory and Decision. 68 (4): 445–462. doi:10.1007/s11238-008-9106-2.
- ^ Xue, G.; Lu, Z.; Levin, I. P.; Bechara, A. (2011). “An fMRI study of risk-taking following wins and losses: Implications for the gambler's fallacy”. Human Brain Mapping. 32 (2): 271–281. doi:10.1002/hbm.21015. PMC 3429350. PMID 21229615.
- ^ Beach, L. R.; Swensson, R. G. (1967). “Instructions about randomness and run dependency in two-choice learning”. Journal of Experimental Psychology. 75 (2): 279–282. doi:10.1037/h0024979. PMID 6062970.
- ^ Fischbein, E.; Schnarch, D. (1997). “The evolution with age of probabilistic, intuitively based misconceptions”. Journal for Research in Mathematics Education. 28 (1): 96–105. doi:10.2307/749665. JSTOR 749665.
- ^ Roney, C. J.; Trick, L. M. (2003). “Grouping and gambling: A gestalt approach to understanding the gambler's fallacy”. Canadian Journal of Experimental Psychology. 57 (2): 69–75. doi:10.1037/h0087414. PMID 12822837.
- ^ a b Chen, Daniel; Moskowitz, Tobias J.; Shue, Kelly (ngày 24 tháng 3 năm 2016). “Decision-Making Under the Gambler's Fallacy: Evidence from Asylum Judges, Loan Officers, and Baseball Umpires*”. The Quarterly Journal of Economics (bằng tiếng Anh). 131 (3): 1181–1242. doi:10.1093/qje/qjw017. ISSN 0033-5533.
- ^ Cole, Shawn; Kanz, Martin; Kapper, Leora (2015). “Incentivizing Calculated Risk-Taking: Evidence from an Experiment with Commercial Bank Loan Officers”. Journal of Finance: 537–575.
- ^ a b Terrell, Dek (tháng 10 năm 1994). “A test of the gambler's fallacy: evidence from pari-mutuel games”. Insurance: Mathematics and Economics. 15 (1): 83–84. doi:10.1016/0167-6687(94)90729-3. ISSN 0167-6687.
- ^ a b Clotfelter, Charles; Cook, Philip (1991). “The "Gambler's Fallacy" in lottery play”. National Bureau of Economic Research: 1–15.



![{\displaystyle 1-\left[{\frac {15}{16}}\right]^{16}\,=\,64.39\%}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d791f63cddc590830c6ef468bbf823c14c1953f)
![{\displaystyle 1-\left[{\frac {15}{16}}\right]^{15}\,=\,62.02\%}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b0b7ce6d128c5742499914574afc8e625b73af1)