phép biến đổi Laplace của hàm f(t) = t và ảnh của nó là hàm F(s) = 1/s^2. F(s) cũng chính là phần diện tích bên dưới đường cong y = t.e^(-st) Biến đổi Laplace (Tiếng Anh : Laplace transform ) là một biến đổi tích phân của hàm số
f
(
t
)
{\displaystyle f(t)}
thời gian sang miền tần số phức
F
(
s
)
{\displaystyle F(s)}
nhà toán học người Pháp Pierre-Simon Laplace . Cùng với biến đổi Fourier , phép biến đổi này là một trong hai biến đổi hữu ích trong việc giải các bài toán vật lý , bằng cách đơn giản hóa các phép toán giải tích phức tạp như đạo hàm , tích phân thành các phép tính đại số (giống như cách mà hàm logarit chuyển một phép toán nhân các số thành phép cộng các logarit của chúng). Vì vậy nó đặc biệt hữu ích trong giải các phương trình vi phân , phương trình đạo hàm riêng, phương trình tích phân, và những phương trình thường xuất hiện trong các bài toán vật lý, trong phân tích mạch điện, xử lý số liệu, dao động điều hòa, các hệ cơ học,... Bởi vì qua biến đổi Laplace các phương trình này có thể trở thành các phương trình đại số đơn giản hơn. Đối với các nghiệm của hàm ảnh trong không gian p , chúng ta dùng biến đổi Laplace ngược để có lại hàm gốc trong không gian thực t .
Từ năm 1744, nhà toán học người Thụy Sĩ Leonhard Euler đã đưa ra các tích phân dưới đây để giải các phương trình vi phân:
z
=
∫
X
(
x
)
e
a
x
d
x
{\displaystyle z=\int X(x)e^{ax}dx}
z
=
∫
X
(
x
)
x
A
d
x
{\displaystyle z=\int X(x)x^{A}dx}
Năm 1773, nhà toán học người Pháp gốc Ý Joseph-Louis Lagrange , một người rất ngưỡng mộ Euler, đã nghiên cứu cách tính tích phân của hàm mật độ xác suất và đưa ra biểu thức tích phân:
∫
X
(
x
)
e
a
x
a
x
d
x
{\displaystyle \int X(x)e^{ax}a^{x}dx}
Năm 1782, Laplace đã chú ý đến các dạng tích phân này khi ông tiếp tục công trình của Euler là sử dụng phép tính tích phân để giải phương trình. Đến năm 1785, vượt ra khỏi giới hạn giải quyết các phương trình bằng phương pháp tích phân, ông đã đưa ra các biến đổi mà sẽ trở nên phổ biến về sau, với phép tích phân:
∫
x
s
Φ
(
s
)
d
x
{\displaystyle \int x^{s}\Phi \ (s)dx}
Nó tương tự với biến đổi Mellin , bằng cách biến đổi phương trình sai phân để giải phương trình biến đổi. Với cách thức tương tự, Laplace đã suy ra các tính chất của biến đổi Laplace. Ông cũng nhận ra rằng phương pháp của Joseph Fourier trong chuỗi Fourier để giải phương trình khuếch tán chỉ có thể áp dụng trong một vùng không gian giới hạn.
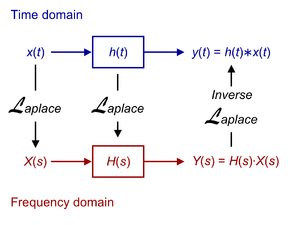
Phép biến đổi Laplace là cách tiếp cận miền tần số cho các tín hiệu thời gian liên tục bất kể tính ổn định của hệ thống. Phép biến đổi Laplace của hàm số f (t )số thực t ≥ 0F (s )
L
{
f
(
t
)
}
=
F
(
s
)
=
∫
0
−
∞
f
(
t
)
e
−
s
t
d
t
{\displaystyle {\mathcal {L}}\{f(t)\}=F(s)=\int \limits _{0^{-}}^{\infty }f(t)e^{-st}dt}
Trong đó:
s
{\displaystyle s}
s
=
σ
+
j
ω
{\displaystyle s=\sigma +j\omega }
s
{\displaystyle s}
s
−
1
{\displaystyle s^{-1}}
Giới hạn
0
−
{\displaystyle 0^{-}}
t
=
0
{\displaystyle t=0}
f
(
t
)
{\displaystyle f(t)}
t
=
0
{\displaystyle t=0}
Một khi nói "biến đổi Laplace" mà không chú ý thêm gì, thường là ta nói đến biến đổi một phía. Biến đổi Laplace có thể được định nghĩa là biến đổi Laplace hai phía bằng cách mở rộng giới hạn của tích phân đến vô cực .
F
(
s
)
=
L
{
f
(
t
)
}
=
∫
−
∞
∞
f
(
t
)
e
−
s
t
d
t
{\displaystyle F(s)={\mathcal {L}}\left\{f(t)\right\}=\int _{-\infty }^{\infty }f(t)e^{-st}dt}
Như vậy, biến đổi Laplace một phía đơn giản sẽ trở thành trường hợp đặc biệt của biến đổi Laplace hai phía, được xác định bằng cách lấy hàm đã chuyển đổi nhân với hàm bước nhảy Heaviside .
Biến đổi Laplace ngược giúp chúng ta tìm lại hàm gốc f(t) từ hàm ảnh F(s). Biến đổi Laplace ngược được định nghĩa bởi tích phân sau.
L
−
1
{
F
(
s
)
}
=
f
(
t
)
=
1
2
π
i
∫
γ
−
i
∞
γ
+
i
∞
e
s
t
F
(
s
)
d
s
{\displaystyle {\mathcal {L}}^{-1}\left\{F(s)\right\}=f(t)={\frac {1}{2\pi i}}\int _{\gamma -i\infty }^{\gamma +i\infty }e^{st}F(s)ds}
Nhưng thông thường chúng ta ít dùng đến tích phân này để tính hàm gốc mà dùng bảng "các hàm gốc – hàm ảnh tương ứng" đã có sẵn để tìm lại hàm gốc f(t).
Tập hợp các hàm f của biến số thực t sao cho tích phân
∫
0
∞
f
(
t
)
e
−
s
t
d
t
{\displaystyle \int _{0}^{\infty }f(t)e^{-st}dt}
∫
0
∞
f
(
t
)
e
−
s
t
d
t
{\displaystyle \int _{0}^{\infty }f(t)e^{-st}dt}
Ta có thể chứng minh được lớp các hàm gốc phải thỏa mãn các tính chất sau.
f(t) = 0, với mọi t < 0.
Khi t ≥ 0, hàm f(t) liên tục cùng với các đạo hàm cấp đủ lớn trên toàn trục t, trừ một số hữu hạn điểm gián đoạn loại một.
Khi
t
→
+
∞
{\displaystyle t\to +\infty }
|
f
(
t
)
|
≤
M
e
s
t
,
∀
t
>
0
{\displaystyle \left|f(t)\right|\leq Me^{st},\forall t>0}
o = inf {s} được gọi là chỉ số tăng của hàm f. (Tức là hàm f(t) không được tăng nhanh hơn hàm est để đảm bảo tích phân Laplace hội tụ). Tính chất của biến đổi Laplace [ sửa | sửa mã nguồn ] Cho các hàm f(t) và g(t), và các hàm ảnh tương ứng F(s) và G(s):
f
(
t
)
=
L
−
1
{
F
(
s
)
}
{\displaystyle f(t)={\mathcal {L}}^{-1}\left\{F(s)\right\}}
g
(
t
)
=
L
−
1
{
G
(
s
)
}
{\displaystyle g(t)={\mathcal {L}}^{-1}\left\{G(s)\right\}}
Sau đây là bảng các tính chất của biến đổi Laplace:
TÍNH CHẤT
MIỀN THỜI GIAN
MIỀN TẦN SỐ
Tuyến tính
a
f
(
t
)
+
b
g
(
t
)
{\displaystyle af(t)+bg(t)\ }
a
F
(
s
)
+
b
G
(
s
)
{\displaystyle aF(s)+bG(s)\ }
Đạo hàm trong miền tần số
t
f
(
t
)
{\displaystyle tf(t)\ }
−
F
′
(
s
)
{\displaystyle -F'(s)\ }
Đạo hàm bậc n trong miền tần số
t
n
f
(
t
)
{\displaystyle t^{n}f(t)\ }
(
−
1
)
n
F
(
n
)
(
s
)
{\displaystyle (-1)^{n}F^{(n)}(s)\ }
Đạo hàm trong miền thời gian
f
′
(
t
)
{\displaystyle f'(t)\ }
s
F
(
s
)
−
f
(
0
−
)
{\displaystyle sF(s)-f(0^{-})\ }
Đạo hàm bậc 2
f
″
(
t
)
{\displaystyle f''(t)\ }
s
2
F
(
s
)
−
s
f
(
0
−
)
−
f
′
(
0
−
)
{\displaystyle s^{2}F(s)-sf(0^{-})-f'(0^{-})\ }
Tổng quát
f
(
n
)
(
t
)
{\displaystyle f^{(n)}(t)\ }
s
n
F
(
s
)
−
s
n
−
1
f
(
0
−
)
−
⋯
−
f
(
n
−
1
)
(
0
−
)
{\displaystyle s^{n}F(s)-s^{n-1}f(0^{-})-\cdots -f^{(n-1)}(0^{-})\ }
Tích phân trong miền tần số
f
(
t
)
t
{\displaystyle {\frac {f(t)}{t}}\ }
∫
s
∞
F
(
σ
)
d
σ
{\displaystyle \int _{s}^{\infty }F(\sigma )\,d\sigma \ }
Tích phân trong miền thời gian
∫
0
t
f
(
τ
)
d
τ
=
u
(
t
)
∗
f
(
t
)
{\displaystyle \int _{0}^{t}f(\tau )\,d\tau =u(t)*f(t)}
1
s
F
(
s
)
{\displaystyle {1 \over s}F(s)}
Đồng dạng
f
(
a
t
)
{\displaystyle f(at)\ }
1
|
a
|
F
(
s
a
)
{\displaystyle {1 \over |a|}F\left({s \over a}\right)}
Biến đổi trong miền tần số
e
a
t
f
(
t
)
{\displaystyle e^{at}f(t)\ }
F
(
s
−
a
)
{\displaystyle F(s-a)\ }
Biến đổi trong miền thời gian
f
(
t
−
a
)
u
(
t
−
a
)
{\displaystyle f(t-a)u(t-a)\ }
e
−
a
s
F
(
s
)
{\displaystyle e^{-as}F(s)\ }
Tích chập
(
f
∗
g
)
(
t
)
{\displaystyle (f*g)(t)\ }
F
(
s
)
⋅
G
(
s
)
{\displaystyle F(s)\cdot G(s)\ }
Hàm tuần hoàn
f
(
t
)
{\displaystyle f(t)\ }
1
1
−
e
−
T
s
∫
0
T
e
−
s
t
f
(
t
)
d
t
{\displaystyle {1 \over 1-e^{-Ts}}\int _{0}^{T}e^{-st}f(t)\,dt}
Định lý giá trị ban đầu: (Định lý giới hạn)
f
(
0
+
)
=
lim
s
→
∞
s
F
(
s
)
{\displaystyle f(0^{+})=\lim _{s\to \infty }{sF(s)}}
Định lý giá trị cuối: (Định lý giới hạn)
f
(
∞
)
=
lim
s
→
0
s
F
(
s
)
{\displaystyle f(\infty )=\lim _{s\to 0}{sF(s)}}
Biến đổi Laplace của phép đạo hàm của một hàm [ sửa | sửa mã nguồn ] Thường dùng phép tính vi phân của biến đổi Laplace để tìm dạng đạo hàm của một hàm. Ta có thể thu được từ biểu thức cơ bản đối với biến đổi Laplace như sau:
L
{
f
(
t
)
}
=
∫
0
−
+
∞
e
−
s
t
f
(
t
)
d
t
{\displaystyle {\mathcal {L}}\left\{f(t)\right\}=\int _{0^{-}}^{+\infty }e^{-st}f(t)\,dt}
=
[
f
(
t
)
e
−
s
t
−
s
]
0
−
+
∞
−
∫
0
−
+
∞
e
−
s
t
−
s
f
′
(
t
)
d
t
{\displaystyle ~~=\left[{\frac {f(t)e^{-st}}{-s}}\right]_{0^{-}}^{+\infty }-\int _{0^{-}}^{+\infty }{\frac {e^{-st}}{-s}}f'(t)dt}
=
[
−
f
(
0
)
−
s
]
+
1
s
L
{
f
′
(
t
)
}
,
{\displaystyle ~~=\left[-{\frac {f(0)}{-s}}\right]+{\frac {1}{s}}{\mathcal {L}}\left\{f'(t)\right\},}
L
{
d
f
d
t
}
=
s
⋅
L
{
f
(
t
)
}
−
f
(
0
)
,
{\displaystyle {\mathcal {L}}\left\{{\frac {df}{dt}}\right\}=s\cdot {\mathcal {L}}\left\{f(t)\right\}-f(0),}
Trong trường hợp 2 bên, ta có
L
{
d
f
d
t
}
=
s
∫
−
∞
+
∞
e
−
s
t
f
(
t
)
d
t
=
s
⋅
L
{
f
(
t
)
}
.
{\displaystyle {\mathcal {L}}\left\{{df \over dt}\right\}=s\int _{-\infty }^{+\infty }e^{-st}f(t)\,dt=s\cdot {\mathcal {L}}\{f(t)\}.}
Liên hệ với các biến đổi khác [ sửa | sửa mã nguồn ] Biến đổi Fourier liên tục tương đương với giá trị của biến đổi Laplace hai bên với argument là số phức s = iω hay
s
=
2
π
f
i
{\displaystyle s=2\pi fi}
F
(
ω
)
=
F
{
f
(
t
)
}
=
L
{
f
(
t
)
}
|
s
=
i
ω
=
F
(
s
)
|
s
=
i
ω
=
∫
−
∞
+
∞
e
−
ı
ω
t
f
(
t
)
d
t
.
{\displaystyle {\begin{array}{rcl}F(\omega )&=&{\mathcal {F}}\left\{f(t)\right\}\\[1em]&=&{\mathcal {L}}\left\{f(t)\right\}|_{s=i\omega }=F(s)|_{s=i\omega }\\[1em]&=&\int _{-\infty }^{+\infty }e^{-\imath \omega t}f(t)\,\mathrm {d} t.\\\end{array}}}
Chú ý biểu thức này không tính đến hệ số tỉ lệ
1
2
π
{\displaystyle {\frac {1}{\sqrt {2\pi }}}}
Mối quan hệ này giữa biến đổi Laplace và biến đổi Fourier thường được dùng để xác định quang phổ tần số của một tín hiệu hay hệ thống động lực học (dynamic system ).
Biến đổi Mellin và phép nghịch đảo của nó liên hệ với biến đổi Laplace hai bên bằng cách thay đổi biến. Trong biến đổi Mellin
G
(
s
)
=
M
{
g
(
θ
)
}
=
∫
0
∞
θ
s
g
(
θ
)
d
θ
θ
{\displaystyle G(s)={\mathcal {M}}\left\{g(\theta )\right\}=\int _{0}^{\infty }\theta ^{s}g(\theta ){\frac {d\theta }{\theta }}}
Ta đặt θ = e-t , ta sẽ thu được biến đổi Laplace hai bên.
Biến đổi Z là biến đổi Laplace của một tín hiệu thử lý tưởng bằng cách thay thế:
z
=
d
e
f
e
s
T
{\displaystyle z\ {\stackrel {\mathrm {def} }{=}}\ e^{sT}\ }
T
=
1
/
f
s
{\displaystyle T=1/f_{s}\ }
f
s
{\displaystyle f_{s}\ }
đặt
Δ
T
(
t
)
=
d
e
f
∑
n
=
0
∞
δ
(
t
−
n
T
)
{\displaystyle \Delta _{T}(t)\ {\stackrel {\mathrm {def} }{=}}\ \sum _{n=0}^{\infty }\delta (t-nT)}
lực Dirac ).và
x
q
(
t
)
=
d
e
f
x
(
t
)
Δ
T
(
t
)
=
x
(
t
)
∑
n
=
0
∞
δ
(
t
−
n
T
)
{\displaystyle x_{q}(t)\ {\stackrel {\mathrm {def} }{=}}\ x(t)\Delta _{T}(t)=x(t)\sum _{n=0}^{\infty }\delta (t-nT)}
=
∑
n
=
0
∞
x
(
n
T
)
δ
(
t
−
n
T
)
=
∑
n
=
0
∞
x
[
n
]
δ
(
t
−
n
T
)
{\displaystyle =\sum _{n=0}^{\infty }x(nT)\delta (t-nT)=\sum _{n=0}^{\infty }x[n]\delta (t-nT)}
là sự biểu diễn liên tục thời gian (continuous-time ) của x(t) còn
x
[
n
]
=
d
e
f
x
(
n
T
)
{\displaystyle x[n]\ {\stackrel {\mathrm {def} }{=}}\ x(nT)\ }
Biến đổi Laplace đối với tín hiệu thử xq (t) là
X
q
(
s
)
=
∫
0
−
∞
x
q
(
t
)
e
−
s
t
d
t
{\displaystyle X_{q}(s)=\int _{0^{-}}^{\infty }x_{q}(t)e^{-st}\,dt}
=
∫
0
−
∞
∑
n
=
0
∞
x
[
n
]
δ
(
t
−
n
T
)
e
−
s
t
d
t
{\displaystyle \ =\int _{0^{-}}^{\infty }\sum _{n=0}^{\infty }x[n]\delta (t-nT)e^{-st}\,dt}
=
∑
n
=
0
∞
x
[
n
]
∫
0
−
∞
δ
(
t
−
n
T
)
e
−
s
t
d
t
{\displaystyle \ =\sum _{n=0}^{\infty }x[n]\int _{0^{-}}^{\infty }\delta (t-nT)e^{-st}\,dt}
=
∑
n
=
0
∞
x
[
n
]
e
−
n
s
T
.
{\displaystyle \ =\sum _{n=0}^{\infty }x[n]e^{-nsT}.}
Đây là định nghĩa chính xác của biến đổi Z đối với hàm x[n].
X
(
z
)
=
∑
n
=
0
∞
x
[
n
]
z
−
n
{\displaystyle X(z)=\sum _{n=0}^{\infty }x[n]z^{-n}}
z
←
e
s
T
{\displaystyle z\leftarrow e^{sT}\ }
So sánh 2 phương trình cuối ta thấy mối liên hệ giữa biến đổi Z và biến đổi Laplace của tín hiệu thử
X
q
(
s
)
=
X
(
z
)
|
z
=
e
s
T
.
{\displaystyle X_{q}(s)=X(z){\Big |}_{z=e^{sT}}.}
Dạng tích phân của biến đổi Borel có liên hệ với biến đổi Laplace; thật sự, có một số nhầm lẫn khi cho rằng chúng tương tự như nhau. Biến đổi Borel tổng quát tạo ra biến đổi Laplace cho những hàm không phải hàm mũ .
Từ biến đổi Laplace ban đầu có thể xem như là trường hợp đặc biệt của biến đổi hai bên, và từ biến đổi hai bên có thể xem như là tổng của hai biến đổi một bên, điểm khác biệt riêng của các biến đổi Laplace, Fourier, Mellin, Z ở trên là sự liên quan của từng biến đổi đối với biến đổi tích phân.
Vì biến đổi Laplace là một toán tử tuyến tính nên
Biến đổi Laplace của tổng bằng tổng các biến đổi Laplace của các số hạng
L
{
f
(
t
)
+
g
(
t
)
}
=
L
{
f
(
t
)
}
+
L
{
g
(
t
)
}
{\displaystyle {\mathcal {L}}\left\{f(t)+g(t)\right\}={\mathcal {L}}\left\{f(t)\right\}+{\mathcal {L}}\left\{g(t)\right\}}
Biến đổi Laplace của một bội số của hàm bằng bội số nhân cho biến đổi Laplace của hàm đó
L
{
a
f
(
t
)
}
=
a
L
{
f
(
t
)
}
{\displaystyle {\mathcal {L}}\left\{af(t)\right\}=a{\mathcal {L}}\left\{f(t)\right\}}
Tính đơn ánh của biến đổi Laplace chỉ đúng khi t là số không âm, vì thế các hàm trong miền thời gian ở bảng dưới là bội của hàm bậc thang Heaviside u(t).
Bảng cung cấp những biến đổi Laplace đối với những hàm chung một biến.
STT
Hàm
Hàm gốc (miền t)
x
(
t
)
=
L
−
1
{
X
(
s
)
}
{\displaystyle x(t)={\mathcal {L}}^{-1}\left\{X(s)\right\}}
Hàm ảnh (miền s)
X
(
s
)
=
L
{
x
(
t
)
}
{\displaystyle X(s)={\mathcal {L}}\left\{x(t)\right\}}
Miền hội tụ
1
trễ lý tưởng
δ
(
t
−
τ
)
{\displaystyle \delta (t-\tau )\ }
e
−
τ
s
{\displaystyle e^{-\tau s}\ }
1a
xung đơn vị
δ
(
t
)
{\displaystyle \delta (t)\ }
1
{\displaystyle 1\ }
mọi s
2
trễ mũ n
(
t
−
τ
)
n
n
!
e
−
α
(
t
−
τ
)
⋅
u
(
t
−
τ
)
{\displaystyle {\frac {(t-\tau )^{n}}{n!}}e^{-\alpha (t-\tau )}\cdot u(t-\tau )}
e
−
τ
s
(
s
+
α
)
n
+
1
{\displaystyle {\frac {e^{-\tau s}}{(s+\alpha )^{n+1}}}}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\,}
2a
mũ n n )
t
n
n
!
⋅
u
(
t
)
{\displaystyle {t^{n} \over n!}\cdot u(t)}
1
s
n
+
1
{\displaystyle {1 \over s^{n+1}}}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\,}
2a.1
mũ q q )
t
q
Γ
(
q
+
1
)
⋅
u
(
t
)
{\displaystyle {t^{q} \over \Gamma (q+1)}\cdot u(t)}
1
s
q
+
1
{\displaystyle {1 \over s^{q+1}}}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\,}
2a.2
bậc thang đơn vị
u
(
t
)
{\displaystyle u(t)\ }
1
s
{\displaystyle {1 \over s}}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\,}
2b
bậc thang đơn vị có trễ
u
(
t
−
τ
)
{\displaystyle u(t-\tau )\ }
e
−
τ
s
s
{\displaystyle {e^{-\tau s} \over s}}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\,}
2c
dốc
t
⋅
u
(
t
)
{\displaystyle t\cdot u(t)\ }
1
s
2
{\displaystyle {\frac {1}{s^{2}}}}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\,}
2d
mũ n với dịch chuyển tần số
t
n
n
!
e
−
α
t
⋅
u
(
t
)
{\displaystyle {\frac {t^{n}}{n!}}e^{-\alpha t}\cdot u(t)}
1
(
s
+
α
)
n
+
1
{\displaystyle {\frac {1}{(s+\alpha )^{n+1}}}}
Re
{
s
}
>
−
α
{\displaystyle {\textrm {Re}}\{s\}>-\alpha \,}
2d.1
suy giảm hàm mũ
e
−
α
t
⋅
u
(
t
)
{\displaystyle e^{-\alpha t}\cdot u(t)\ }
1
s
+
α
{\displaystyle {1 \over s+\alpha }}
Re
{
s
}
>
−
α
{\displaystyle {\textrm {Re}}\{s\}>-\alpha \ }
3
tiệm cận hàm mũ
(
1
−
e
−
α
t
)
⋅
u
(
t
)
{\displaystyle (1-e^{-\alpha t})\cdot u(t)\ }
α
s
(
s
+
α
)
{\displaystyle {\frac {\alpha }{s(s+\alpha )}}}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\ }
4
sine
sin
(
ω
t
)
⋅
u
(
t
)
{\displaystyle \sin(\omega t)\cdot u(t)\ }
ω
s
2
+
ω
2
{\displaystyle {\omega \over s^{2}+\omega ^{2}}}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\ }
5
cosine
cos
(
ω
t
)
⋅
u
(
t
)
{\displaystyle \cos(\omega t)\cdot u(t)\ }
s
s
2
+
ω
2
{\displaystyle {s \over s^{2}+\omega ^{2}}}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\ }
6
hyperbolic sine
sinh
(
α
t
)
⋅
u
(
t
)
{\displaystyle \sinh(\alpha t)\cdot u(t)\ }
α
s
2
−
α
2
{\displaystyle {\alpha \over s^{2}-\alpha ^{2}}}
Re
{
s
}
>
|
α
|
{\displaystyle {\textrm {Re}}\{s\}>|\alpha |\ }
7
hyperbolic cosine
cosh
(
α
t
)
⋅
u
(
t
)
{\displaystyle \cosh(\alpha t)\cdot u(t)\ }
s
s
2
−
α
2
{\displaystyle {s \over s^{2}-\alpha ^{2}}}
Re
{
s
}
>
|
α
|
{\displaystyle {\textrm {Re}}\{s\}>|\alpha |\ }
8
hàm sine
e
α
t
sin
(
ω
t
)
⋅
u
(
t
)
{\displaystyle e^{\alpha t}\sin(\omega t)\cdot u(t)\ }
ω
(
s
−
α
)
2
+
ω
2
{\displaystyle {\omega \over (s-\alpha )^{2}+\omega ^{2}}}
Re
{
s
}
>
α
{\displaystyle {\textrm {Re}}\{s\}>\alpha \ }
9
hàm cosine
e
α
t
cos
(
ω
t
)
⋅
u
(
t
)
{\displaystyle e^{\alpha t}\cos(\omega t)\cdot u(t)\ }
s
−
α
(
s
−
α
)
2
+
ω
2
{\displaystyle {s-\alpha \over (s-\alpha )^{2}+\omega ^{2}}}
Re
{
s
}
>
α
{\displaystyle {\textrm {Re}}\{s\}>\alpha \ }
10
căn bậc n
t
n
⋅
u
(
t
)
{\displaystyle {\sqrt[{n}]{t}}\cdot u(t)}
s
−
(
n
+
1
)
/
n
⋅
Γ
(
1
+
1
n
)
{\displaystyle s^{-(n+1)/n}\cdot \Gamma \left(1+{\frac {1}{n}}\right)}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\,}
11
logarit tự nhiên
ln
(
t
t
0
)
⋅
u
(
t
)
{\displaystyle \ln \left({t \over t_{0}}\right)\cdot u(t)}
−
t
0
s
[
ln
(
t
0
s
)
+
γ
]
{\displaystyle -{t_{0} \over s}\ [\ \ln(t_{0}s)+\gamma \ ]}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\,}
12
hàm Bessel n
J
n
(
ω
t
)
⋅
u
(
t
)
{\displaystyle J_{n}(\omega t)\cdot u(t)}
ω
n
(
s
+
s
2
+
ω
2
)
−
n
s
2
+
ω
2
{\displaystyle {\frac {\omega ^{n}\left(s+{\sqrt {s^{2}+\omega ^{2}}}\right)^{-n}}{\sqrt {s^{2}+\omega ^{2}}}}}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\,}
(
n
>
−
1
)
{\displaystyle (n>-1)\,}
13
hàm Bessel biến đổi n
I
n
(
ω
t
)
⋅
u
(
t
)
{\displaystyle I_{n}(\omega t)\cdot u(t)}
ω
n
(
s
+
s
2
−
ω
2
)
−
n
s
2
−
ω
2
{\displaystyle {\frac {\omega ^{n}\left(s+{\sqrt {s^{2}-\omega ^{2}}}\right)^{-n}}{\sqrt {s^{2}-\omega ^{2}}}}}
Re
{
s
}
>
|
ω
|
{\displaystyle {\textrm {Re}}\{s\}>|\omega |\,}
14
hàm Bessel
Y
0
(
α
t
)
⋅
u
(
t
)
{\displaystyle Y_{0}(\alpha t)\cdot u(t)}
−
2
sinh
−
1
(
s
/
α
)
π
s
2
+
α
2
{\displaystyle -{2\sinh ^{-1}(s/\alpha ) \over \pi {\sqrt {s^{2}+\alpha ^{2}}}}}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\,}
15
hàm Bessel biến đổi
K
0
(
α
t
)
⋅
u
(
t
)
{\displaystyle K_{0}(\alpha t)\cdot u(t)}
16
hàm sai số
e
r
f
(
t
)
⋅
u
(
t
)
{\displaystyle \mathrm {erf} (t)\cdot u(t)}
e
s
2
/
4
(
1
−
erf
(
s
/
2
)
)
s
{\displaystyle {e^{s^{2}/4}\left(1-\operatorname {erf} \left(s/2\right)\right) \over s}}
Re
{
s
}
>
0
{\displaystyle {\textrm {Re}}\{s\}>0\,}
chú thích:
t
{\displaystyle t\,}
s
{\displaystyle s\,}
số phức angular frequency và Re(s) là phần thực của s).
α
{\displaystyle \alpha \,}
β
{\displaystyle \beta \,}
τ
{\displaystyle \tau \,}
ω
{\displaystyle \omega \,}
số thực .
n
{\displaystyle n\,}
nguyên .
Trở kháng và sơ đồ mạch điện tương đương trong mạch miền s [ sửa | sửa mã nguồn ] Biến đổi Laplace được sử dụng để biến đổi các yếu tố mạch điện từ miền thời gian t sang mạch miền s
Bảng so sánh giữa mạch miền t và mạch miền s Mối quan hệ dòng áp trong miền s của các yếu tố mạch điện RLC
V
R
(
s
)
=
R
.
I
(
s
)
{\displaystyle V_{R}(s)=R.I(s)}
V
L
(
s
)
=
s
.
L
.
I
(
s
)
−
L
.
I
o
{\displaystyle V_{L}(s)=s.L.I(s)-L.I_{o}}
V
C
(
s
)
=
1
s
.
C
I
(
s
)
+
V
o
s
{\displaystyle V_{C}(s)={\frac {1}{s.C}}I(s)+{\frac {V_{o}}{s}}}
Chú ý : đối với điện trở R, mạch miền t và mạch miền s giống nhau. Riêng đối với cuộn cảm L và tụ điện C cần phải kể đến nguồn điều kiện ban đầu (dòng ban đầu đối với cuộn cảm và áp ban đầu đối với tụ điện)
Ứng dụng các tính chất và định lý của biến đổi Laplace [ sửa | sửa mã nguồn ] Biến đổi Laplace được sử dụng nhiều trong kỹ thuật và vật lý học . Việc tính toán được chuyển sang không gian Laplace nhằm chuyển phép nhân chập về phép nhân thông thường, khi đó ta có thể giải quyết vấn đề bằng phương pháp đại số.
Biến đổi Laplace còn được sử dụng để giải phương trình vi phân và được ứng dụng rộng rãi trong kỹ thuật điện (electrical engineering ). Phương pháp sử dụng biến đổi Laplace để giải phương trình vi phân được phát triển bởi kỹ sư người Anh Oliver Heaviside .
Những ví dụ dưới đây được sử dụng trong hệ đơn vị SI
Bài toán trong vật lý hạt nhân nguyên tử
Phương trình biểu diễn sự phân rã phóng xạ của một chất đồng vị phóng xạ
d
N
d
t
=
−
λ
N
{\displaystyle {\frac {dN}{dt}}=-\lambda N}
λ
{\displaystyle \lambda }
hằng số phân rã
Ta sẽ sử dụng biến đổi Laplace để giải phương trình này
Từ (1) ta có
d
N
d
t
+
λ
N
=
0
{\displaystyle {\frac {dN}{dt}}+\lambda N=0}
Thực hiện biến đổi Laplace cho cả hai vế của phương trình
(
s
N
~
(
s
)
−
N
o
)
+
λ
N
~
(
s
)
=
0
{\displaystyle \left(s{\tilde {N}}(s)-N_{o}\right)+\lambda {\tilde {N}}(s)\ =\ 0}
Với
N
~
(
s
)
=
L
{
N
(
t
)
}
{\displaystyle {\tilde {N}}(s)={\mathcal {L}}\{N(t)\}}
N
o
=
N
(
0
)
.
{\displaystyle N_{o}\ =\ N(0).}
Giải phương trình ta có
N
~
(
s
)
=
N
o
s
+
λ
.
{\displaystyle {\tilde {N}}(s)={N_{o} \over s+\lambda }.}
Cuối cùng ta thực hiện biến đổi ngược để chuyển về miền t
N
(
t
)
=
L
−
1
{
N
~
(
s
)
}
=
L
−
1
{
N
o
s
+
λ
}
{\displaystyle N(t)\ ={\mathcal {L}}^{-1}\{{\tilde {N}}(s)\}={\mathcal {L}}^{-1}\left\{{\frac {N_{o}}{s+\lambda }}\right\}}
Tổng trở Z(s) của tụ điện và cuộn cảm [ sửa | sửa mã nguồn ] Ví dụ này dựa vào lý thuyết giải tích mạch điện (electrical circuit )
Quan hệ dòng áp của các phần tử RLC trong miền thời gian t
i
R
(
t
)
=
V
R
(
t
)
R
{\displaystyle i_{R}(t)={\frac {V_{R}(t)}{R}}}
i
C
(
t
)
=
C
.
d
V
C
(
t
)
d
t
{\displaystyle i_{C}(t)=C.{\frac {dV_{C}(t)}{dt}}}
V
L
(
t
)
=
L
.
d
i
L
(
t
)
d
t
{\displaystyle V_{L}(t)=L.{\frac {di_{L}(t)}{dt}}}
Với i(t) là lượng điện tích chạy qua các thành phần RLC trong một đơn vị thời gian và V(t) là điện áp giữa 2 đầu từng thành phần RLC, cũng là hàm theo thời gian t
Dùng biến đổi Laplace để chuyển sang miền s
V
R
(
s
)
=
R
.
I
)
(
s
)
{\displaystyle V_{R}(s)=R.I)(s)}
V
L
(
s
)
=
s
.
L
.
I
(
s
)
−
L
.
I
o
{\displaystyle V_{L}(s)=s.L.I(s)-L.I_{o}}
V
C
(
s
)
=
1
s
C
I
(
s
)
+
V
o
s
{\displaystyle V_{C}(s)={\frac {1}{sC}}I(s)+{\frac {V_{o}}{s}}}
Với
I
(
s
)
=
L
i
(
t
)
{\displaystyle I(s)={\mathcal {L}}{i(t)}}
V
(
s
)
=
L
v
(
t
)
{\displaystyle V(s)={\mathcal {L}}{v(t)}}
I
o
=
i
(
0
)
{\displaystyle I_{o}=i(0)}
cuộn cảm L
V
o
=
V
C
(
0
)
{\displaystyle V_{o}=V_{C}(0)}
tụ điện C
Tổng trở Z(s) được định nghĩa là tỷ số giữa áp V và dòng i khi điều kiện ban đầu bằng 0
Z
(
s
)
=
V
(
s
)
I
(
s
)
|
V
o
=
0
.
{\displaystyle Z(s)={V(s) \over I(s)}{\bigg |}_{V_{o}=0}.}
Từ đây ta suy ra tổng trở của các thành phần RLC
Z
R
(
s
)
=
R
{\displaystyle Z_{R}(s)=R}
Z
L
(
s
)
=
s
.
L
{\displaystyle Z_{L}(s)=s.L}
Z
C
(
s
)
=
1
s
C
{\displaystyle Z_{C}(s)={\frac {1}{sC}}}
Sự liên hệ giữa miền thời gian t và miền tần số được biểu diễn thông qua bảng sau:
Chú ý rằng ký hiệu * trong miền thời gian chính là phép nhân chập
Xét hệ tuyến tính bất biến theo thời gian với
h
(
t
)
=
A
e
−
α
t
cos
(
ω
d
t
−
ϕ
d
)
{\displaystyle h(t)=Ae^{-\alpha t}\cos(\omega _{d}t-\phi _{d})}
ω
d
t
−
ϕ
d
≥
0
{\displaystyle \omega _{d}t-\phi _{d}\geq 0}
0
≤
ϕ
d
≤
2
π
{\displaystyle 0\leq \phi _{d}\leq 2\pi }
pha
Ta biến đổi (1)
h
(
t
)
=
A
e
−
α
t
cos
[
ω
d
(
t
−
t
d
)
]
⋅
u
(
t
−
t
d
)
{\displaystyle h(t)=Ae^{-\alpha t}\cos \left[\omega _{d}(t-t_{d})\right]\cdot u(t-t_{d})}
Với
t
d
=
ϕ
d
ω
d
{\displaystyle t_{d}={\phi _{d} \over \omega _{d}}}
hàm bước Heaviside .
Hàm truyền H(s) được suy ra bằng cách dùng biến đổi Laplace đối với hàm h(t)
H
(
s
)
=
L
{
h
(
t
)
}
=
A
e
−
s
t
d
(
s
+
α
)
(
s
+
α
)
2
+
ω
d
2
{\displaystyle H(s)\ =\ {\mathcal {L}}\{h(t)\}=Ae^{-st_{d}}{(s+\alpha ) \over (s+\alpha )^{2}+\omega _{d}^{2}}}
=
A
e
−
s
t
d
(
s
+
α
)
(
s
2
+
2
α
s
+
α
2
)
+
ω
d
2
{\displaystyle =\ Ae^{-st_{d}}{(s+\alpha ) \over (s^{2}+2\alpha s+\alpha ^{2})+\omega _{d}^{2}}}
=
A
e
−
s
t
d
(
s
+
α
)
(
s
2
+
2
α
s
+
ω
0
2
)
{\displaystyle =\ Ae^{-st_{d}}{(s+\alpha ) \over (s^{2}+2\alpha s+\omega _{0}^{2})}}
với
ω
0
=
α
2
+
ω
d
2
{\displaystyle \omega _{0}={\sqrt {\alpha ^{2}+\omega _{d}^{2}}}}
Phương pháp khai triển thừa số riêng phần [ sửa | sửa mã nguồn ] Xét hệ tuyến tính bất biến với thời gian và hàm truyền
H
(
s
)
=
1
(
s
+
α
)
(
s
+
β
)
{\displaystyle H(s)={\frac {1}{(s+\alpha )(s+\beta )}}}
h
(
t
)
=
L
−
1
{
H
(
s
)
}
{\displaystyle h(t)={\mathcal {L}}^{-1}\{H(s)\}}
Để thực hiện biến đổi Laplace ngược, ta bắt đầu khai triển H(s) bằng cách sử dụng phương pháp khai triển riêng phần
H
(
s
)
=
1
(
s
+
α
)
(
s
+
β
)
=
P
(
s
+
α
)
+
R
(
s
+
β
)
{\displaystyle H(s)={\frac {1}{(s+\alpha )(s+\beta )}}={P \over (s+\alpha )}+{R \over (s+\beta )}}
P, R là các hằng số chưa biết. Để tìm hằng số này ta dùng đồng nhất thức
s
+
α
s
+
β
=
P
(
s
+
β
)
+
R
(
s
+
α
)
(
s
+
α
)
(
s
+
β
)
{\displaystyle {\frac {s+\alpha }{s+\beta }}={\frac {P(s+\beta )+R(s+\alpha )}{(s+\alpha )(s+\beta )}}}
Từ đây suy ra
P
=
1
(
s
+
β
)
|
s
=
−
α
=
1
(
β
−
α
)
{\displaystyle P=\left.{1 \over (s+\beta )}\right|_{s=-\alpha }={1 \over (\beta -\alpha )}}
và
R
=
1
(
s
+
α
)
|
s
=
−
β
=
1
(
α
−
β
)
=
−
1
(
β
−
α
)
=
−
P
{\displaystyle R=\left.{1 \over (s+\alpha )}\right|_{s=-\beta }={1 \over (\alpha -\beta )}={-1 \over (\beta -\alpha )}=-P}
Thay vào H(s) ta tìm được
H
(
s
)
=
(
1
β
−
α
)
⋅
(
1
(
s
+
α
)
−
1
(
s
+
β
)
)
{\displaystyle H(s)=\left({\frac {1}{\beta -\alpha }}\right)\cdot \left({1 \over (s+\alpha )}-{1 \over (s+\beta )}\right)}
Cuối cùng sử dụng tính chất và bảng biến đổi Laplace, ta thực hiện biến đổi Laplace ngược cho hàm H(s)
h
(
t
)
=
L
−
1
{
H
(
s
)
}
=
1
β
−
α
(
e
−
α
t
−
e
−
β
t
)
{\displaystyle h(t)={\mathcal {L}}^{-1}\{H(s)\}={\frac {1}{\beta -\alpha }}\left(e^{-\alpha t}-e^{-\beta t}\right)}
Tổng hợp hàm sin, cos và hàm mũ [ sửa | sửa mã nguồn ]
Hàm thời gian Biến đổi Laplace
e
−
α
t
[
cos
(
ω
t
)
+
(
β
−
α
ω
)
sin
(
ω
t
)
]
u
(
t
)
{\displaystyle e^{-\alpha t}\left[\cos {(\omega t)}+\left({\frac {\beta -\alpha }{\omega }}\right)\sin {(\omega t)}\right]u(t)}
s
+
β
(
s
+
α
)
2
+
ω
2
{\displaystyle {\frac {s+\beta }{(s+\alpha )^{2}+\omega ^{2}}}}
Ta bắt đầu với hàm biến đổi Laplace
X
(
s
)
=
s
+
β
(
s
+
α
)
2
+
ω
2
{\displaystyle X(s)={\frac {s+\beta }{(s+\alpha )^{2}+\omega ^{2}}}}
Ta tìm hàm ngược của X(s) bằng cách thêm và bớt hằng số vào tử số
X
(
s
)
=
s
+
α
(
s
+
α
)
2
+
ω
2
+
β
−
α
(
s
+
α
)
2
+
ω
2
{\displaystyle X(s)={\frac {s+\alpha }{(s+\alpha )^{2}+\omega ^{2}}}+{\frac {\beta -\alpha }{(s+\alpha )^{2}+\omega ^{2}}}}
Dựa vào định lý dịch chuyển ta có
x
(
t
)
=
e
−
α
t
L
−
1
{
s
s
2
+
ω
2
+
β
−
α
s
2
+
ω
2
}
{\displaystyle x(t)=e^{-\alpha t}{\mathcal {L}}^{-1}\left\{{s \over s^{2}+\omega ^{2}}+{\beta -\alpha \over s^{2}+\omega ^{2}}\right\}}
=
e
−
α
t
L
−
1
{
s
s
2
+
ω
2
+
(
β
−
α
ω
)
(
ω
s
2
+
ω
2
)
}
{\displaystyle =e^{-\alpha t}{\mathcal {L}}^{-1}\left\{{s \over s^{2}+\omega ^{2}}+\left({\beta -\alpha \over \omega }\right)\left({\omega \over s^{2}+\omega ^{2}}\right)\right\}}
=
e
−
α
t
[
L
−
1
{
s
s
2
+
ω
2
}
+
(
β
−
α
ω
)
L
−
1
{
ω
s
2
+
ω
2
}
]
{\displaystyle =e^{-\alpha t}\left[{\mathcal {L}}^{-1}\left\{{s \over s^{2}+\omega ^{2}}\right\}+\left({\beta -\alpha \over \omega }\right){\mathcal {L}}^{-1}\left\{{\omega \over s^{2}+\omega ^{2}}\right\}\right]}
Cuối cùng, dùng biến đổi Laplace cho hàm sin và cos , ta thu được
x
(
t
)
=
e
−
α
t
[
cos
(
ω
t
)
u
(
t
)
+
(
β
−
α
ω
)
sin
(
ω
t
)
u
(
t
)
]
{\displaystyle x(t)=e^{-\alpha t}\left[\cos {(\omega t)}u(t)+\left({\frac {\beta -\alpha }{\omega }}\right)\sin {(\omega t)}u(t)\right]}
x
(
t
)
=
e
−
α
t
[
cos
(
ω
t
)
+
(
β
−
α
ω
)
sin
(
ω
t
)
]
u
(
t
)
{\displaystyle x(t)=e^{-\alpha t}\left[\cos {(\omega t)}+\left({\frac {\beta -\alpha }{\omega }}\right)\sin {(\omega t)}\right]u(t)}
Hàm thời gian Biến đổi Laplace
sin
(
ω
t
+
ϕ
)
{\displaystyle \sin(\omega t+\phi )}
s
sin
ϕ
+
ω
cos
ϕ
s
2
+
ω
2
{\displaystyle {\frac {s\sin \phi +\omega \cos \phi }{s^{2}+\omega ^{2}}}}
cos
(
ω
t
+
ϕ
)
{\displaystyle \cos {(\omega t+\phi )}}
s
cos
ϕ
−
ω
sin
ϕ
s
2
+
ω
2
{\displaystyle {\frac {s\cos \phi -\omega \sin \phi }{s^{2}+\omega ^{2}}}}
Ta bắt đầu với hàm biến đổi Laplace
X
(
s
)
=
s
sin
ϕ
+
ω
cos
ϕ
s
2
+
ω
2
{\displaystyle X(s)={\frac {s\sin \phi +\omega \cos \phi }{s^{2}+\omega ^{2}}}}
Suy ra
X
(
s
)
=
s
sin
ϕ
s
2
+
ω
2
+
ω
cos
ϕ
s
2
+
ω
2
{\displaystyle X(s)={\frac {s\sin \phi }{s^{2}+\omega ^{2}}}+{\frac {\omega \cos \phi }{s^{2}+\omega ^{2}}}}
=
(
sin
ϕ
)
(
s
s
2
+
ω
2
)
+
(
cos
ϕ
)
(
ω
s
2
+
ω
2
)
{\displaystyle \,\,\,\,\,\,=(\sin \phi )\left({\frac {s}{s^{2}+\omega ^{2}}}\right)+(\cos \phi )\left({\frac {\omega }{s^{2}+\omega ^{2}}}\right)}
Thực hiện biến đổi ngược cho X(s), ta có
x
(
t
)
{\displaystyle x(t)\,\!}
=
(
sin
ϕ
)
L
−
1
{
s
s
2
+
ω
2
}
+
(
cos
ϕ
)
L
−
1
{
ω
s
2
+
ω
2
}
{\displaystyle {}=(\sin \phi ){\mathcal {L}}^{-1}\left\{{\frac {s}{s^{2}+\omega ^{2}}}\right\}+(\cos \phi ){\mathcal {L}}^{-1}\left\{{\frac {\omega }{s^{2}+\omega ^{2}}}\right\}}
=
(
sin
ϕ
)
(
cos
ω
t
)
+
(
sin
ω
t
)
(
c
o
s
ϕ
)
.
{\displaystyle {}=(\sin \phi )(\cos \omega t)+(\sin \omega t)(cos\phi ).\,\!}
Áp dụng hệ thức lượng trong tam giác (trigonometric identity )
a
sin
ω
t
+
b
cos
ω
t
=
a
2
+
b
2
⋅
sin
(
ω
t
+
arctan
(
b
/
a
)
)
{\displaystyle a\sin \omega t+b\cos \omega t={\sqrt {a^{2}+b^{2}}}\cdot \sin \left(\omega t+\arctan(b/a)\right)}
Ta suy ra
x
(
t
)
{\displaystyle x(t)\,\!}
=
cos
2
ϕ
+
sin
2
ϕ
⋅
sin
(
ω
t
+
arctan
(
sin
ϕ
cos
ϕ
)
)
{\displaystyle {}={\sqrt {\cos ^{2}\phi +\sin ^{2}\phi }}\cdot \sin \left(\omega t+\arctan \left({\frac {\sin \phi }{\cos \phi }}\right)\right)}
=
sin
(
ω
t
+
ϕ
)
.
{\displaystyle {}=\sin(\omega t+\phi ).\,\!}
Tương tự ta cũng nhận được
L
−
1
{
s
cos
ϕ
−
ω
sin
ϕ
s
2
+
ω
2
}
=
cos
(
ω
t
+
ϕ
)
{\displaystyle {\mathcal {L}}^{-1}\left\{{\frac {s\cos \phi -\omega \sin \phi }{s^{2}+\omega ^{2}}}\right\}=\cos {(\omega t+\phi )}}



















































![{\displaystyle ~~=\left[{\frac {f(t)e^{-st}}{-s}}\right]_{0^{-}}^{+\infty }-\int _{0^{-}}^{+\infty }{\frac {e^{-st}}{-s}}f'(t)dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d09344bdecb5d278b19a9074dff27dab0383a4d1)
![{\displaystyle ~~=\left[-{\frac {f(0)}{-s}}\right]+{\frac {1}{s}}{\mathcal {L}}\left\{f'(t)\right\},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/074c586581569204ce59195c66b2677378d8cd83)



![{\displaystyle {\begin{array}{rcl}F(\omega )&=&{\mathcal {F}}\left\{f(t)\right\}\\[1em]&=&{\mathcal {L}}\left\{f(t)\right\}|_{s=i\omega }=F(s)|_{s=i\omega }\\[1em]&=&\int _{-\infty }^{+\infty }e^{-\imath \omega t}f(t)\,\mathrm {d} t.\\\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72c5373b6a06299010a3a711efc68aba01e889d1)







![{\displaystyle =\sum _{n=0}^{\infty }x(nT)\delta (t-nT)=\sum _{n=0}^{\infty }x[n]\delta (t-nT)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85c04a28bc50f1e8453ba38536b5fd6d10460005)
![{\displaystyle x[n]\ {\stackrel {\mathrm {def} }{=}}\ x(nT)\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/070b84a494ac1284b2ce0e1d24ad955c51a43846)

![{\displaystyle \ =\int _{0^{-}}^{\infty }\sum _{n=0}^{\infty }x[n]\delta (t-nT)e^{-st}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2427b219d2ac5f6d5dfaaa71311849fea754299d)
![{\displaystyle \ =\sum _{n=0}^{\infty }x[n]\int _{0^{-}}^{\infty }\delta (t-nT)e^{-st}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6243d14c2da5e2440901440149d7582a8de9bba9)
![{\displaystyle \ =\sum _{n=0}^{\infty }x[n]e^{-nsT}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c45fe18e6ac2a02b438e3cb908f3f2f7ac1cd3bb)
![{\displaystyle X(z)=\sum _{n=0}^{\infty }x[n]z^{-n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbf7e6d1a9bf26a3017c79040c80295cb1f2eaa1)














































![{\displaystyle {\sqrt[{n}]{t}}\cdot u(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4345a4c33a88daeb8ec5a3002d02d62f66ff3fb)


![{\displaystyle -{t_{0} \over s}\ [\ \ln(t_{0}s)+\gamma \ ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fce40449b6e96562216aebb919341a47876cf15)

















































![{\displaystyle h(t)=Ae^{-\alpha t}\cos \left[\omega _{d}(t-t_{d})\right]\cdot u(t-t_{d})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34b1825f95b43f2c3baaaaf5ea730d6861ea1495)













![{\displaystyle e^{-\alpha t}\left[\cos {(\omega t)}+\left({\frac {\beta -\alpha }{\omega }}\right)\sin {(\omega t)}\right]u(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8fc986650f3808a272ace7b5128ee88c5ad69aa)





![{\displaystyle =e^{-\alpha t}\left[{\mathcal {L}}^{-1}\left\{{s \over s^{2}+\omega ^{2}}\right\}+\left({\beta -\alpha \over \omega }\right){\mathcal {L}}^{-1}\left\{{\omega \over s^{2}+\omega ^{2}}\right\}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16c121beb014d201b33605d4ae3841615d09f941)
![{\displaystyle x(t)=e^{-\alpha t}\left[\cos {(\omega t)}u(t)+\left({\frac {\beta -\alpha }{\omega }}\right)\sin {(\omega t)}u(t)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/381e6130c4b380d3b5810be1093c146e76f95518)
![{\displaystyle x(t)=e^{-\alpha t}\left[\cos {(\omega t)}+\left({\frac {\beta -\alpha }{\omega }}\right)\sin {(\omega t)}\right]u(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0de0f2d3282815a9634b6b092eb77976abc86f94)













