Đường tròn Euler

Chân ba đường cao của một tam giác bất kì, ba trung điểm của ba cạnh, ba trung điểm của ba đoạn thẳng nối ba đỉnh với trực tâm, tất cả chín điểm này cùng nằm trên một đường tròn. Đường tròn này thường được gọi là đường tròn Euler hay còn gọi là đường tròn Feuerbach, đường tròn Terquem hay đường tròn chín điểm, đường tròn trung bình.

Một số tính chất

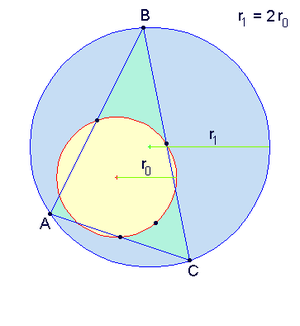
• Gọi R là bán kính đường tròn ngoại tiếp của tam giác thì đường tròn Euler có bán kính là R/2 và tâm của nó là trung điểm đoạn nối trực tâm và tâm đường tròn ngoại tiếp của tam giác đó.
• Nếu có một hệ thống trực giao của 4 điểm đã cho thì các tam giác có đỉnh là 3 trong 4 điểm đó đều có chung đường tròn Euler.
• Các tâm đường tròn nội tiếp và các đường tròn bàng tiếp lập thành một hệ thống trực giao có đường tròn Euler chính là đường tròn ngoại tiếp tam giác gốc.
• Với có bốn điểm phân biệt bất kỳ A,B,C,D thì các đường tròn Euler của các tam giác ABC, BCD, CDA, DAB đồng quy tại một điểm.
• Đường tròn Euler đi qua tâm của các hyperbol Kiepert và Jeřábek.

Định lý Feuerbach

Định lý Feuerbach

Nội dung định lý:

Đường tròn Feuerbach của một tam giác tiếp xúc với đường tròn nội tiếp và ba đường tròn bàng tiếp của tam giác đó.

Liên kết ngoài

Tiếng Anh:

• Encyclopedia of Triangles Centers by Clark Kimberling. The nine-point center is indexed as X(5), the Feuerbach point, as X(11), the center of the Kiepert hyperbola as X(115), and the center of the Jerabek hyperbola as X(125).
• Nine Point Center by Antonio Gutierrez from Geometry Step by Step from the Land of the Incas.
• History about the nine-point circle based on J.S. MacCay's article from 1892: History of the Nine Point Circle
• Nine Point Circle in Java at cut-the-knot
• Feuerbach's Theorem: a Proof at cut-the-knot
• Special lines and circles in a triangle (requires Java)
• An interactive Java applet showing several triangle centers that lies on the Nine Point Circle.

Tiếng Việt:

• Nâng cao và phát triển Toán 9 - Vũ Hữu Bình, NXBGD