Hyperbol

Trong toán học, hyperbol hay hypecbol (từ tiếng Hy Lạp: ὑπερβολή, nghĩa đen là "vượt quá" hay "thái quá") là một kiểu Đường cô-nic, được định nghĩa là đường giao của một mặt nón với một mặt phẳng cắt cả hai nửa của hình nón.

Đường hyperbol còn được nghĩa định là quỹ tích của những điểm trong mặt phẳng có giá trị tuyết đối của hiệu khoảng cách tới hai điểm cố định là một hằng số bằng 2a. a đồng thời cũng bằng độ dài bán trục lớn của Hyberbol. Hai điểm cố định đó gọi là hai tiêu điểm của hyperbol. Đường thẳng đi qua hai tiêu điểm này được gọi là trục thực của hyberbol và trung điểm của đoạn thẳng nối hai tiêu điểm này được gọi là tâm của hình hyperbol.

Hình hyperbol được tạo bởi giao của một mặt phẳng với một mặt nón

Trong đại số, đường hyperbol là một đường cong trên mặt phẳng Descartes được định nghĩa bằng công thức tổng quát

Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0

với $B^{2}>4AC$ , trong đó A, B, C, D, E đều là các hệ số thực, và có nhiều hơn một cách giải, với mỗi điểm (x, y) thuộc hình Hyperbol.

Định nghĩa

Hình hyberbol có thể được định nghĩa theo 3 cách:

Đường giao tạo bởi hai mặt nón với một mặt phẳng khi mặt phẳng cắt cả hai hình nón.
Quỹ tích của các điểm mà hiệu khoảng cách tới hai điểm cho trước (hai tiêu điểm) là một hằng số.
Quỹ tích của các điểm thỏa mãn tỉ lệ khoảng cách từ điểm đó đến tiêu điểm trên khoảng cách từ điểm đó đến một đường thẳng (được gọi là đường chuẩn) là một hằng số lớn hơn 1. Hằng số này được gọi là tâm sai của hyberbol.

Đường hyperbol có hai nhánh với hai tiêu điểm và hai đường tiệm cận. Hai đường tiệm cận đi qua tâm của hình hyperbol có phương trình $y={\frac {bx}{a}}$ và $y=-{\frac {bx}{a}}$

Đường hyperbol có tính chất là một tia bắt đầu tại một tiêu điểm sẽ bị phản xạ qua giao điểm của nó với hyperbol (đường tiếp tuyến với hyperbol tại điểm đó là đường pháp tuyến) tạo thành một đường thẳng đi qua tiêu điểm còn lại, và ngược lại.

Các hình mà theo tên tiếng Anh là *rectangular hyperbola* (xanh lam và xanh lá cây) và các đường tiệm cận (đỏ)

Trường hợp đặc biệt của hyperbol theo tên tiếng Anh được gọi là rectangular hyperbola khi hai đường tiệm cận tạo thành một góc vuông. Hình hyperbol đều với trục tọa độ là các đường tiệm cận được xác định bởi công thức xy= $c^{2}$ , trong đó c là một hằng số (theo hình bên dưới). Điểm nằm trên Hyperbol gần gốc tọa độ nhất có tọa độ là $({\sqrt {c}},{\sqrt {c}})$ . Đồng thời, đường thẳng đi qua gốc tọa độ và điểm đó thì vuông góc với tiếp tuyến tại điểm đó.

Vì hàm số sin và hàm số cos là hàm lượng giác dành cho đường elíp, nên hàm sin của hyperbol và hàm cos của hyperbol là hàm lượng giác của hyperbol.

Công thức

Hình hyper tuyển

Hình Hyperbol nằm theo hướng Đông-Tây với tâm có tọa độ là (h,k):

{\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1

Phương trình chính tắc của đường hyperbol trong hệ tọa độ Descartes khi có tâm trùng với gốc tọa độ:

{\frac {\left(x\right)^{2}}{a^{2}}}-{\frac {\left(y\right)^{2}}{b^{2}}}=1

Trong đó $c^{2}=a^{2}+b^{2}$ và 2c là tiêu cự

Trục thực của hyperbol đi qua tâm của hình hyperbol và cắt các nhánh tại các đỉnh của mỗi nhánh. Các tiêu điểm cũng nằm trên đường thẳng chứa trục thực của hyperbol.
Trục ảo vuông góc với trục thực tại tâm của hyperbol.
Hình chữ nhật cơ sở là hình chữ nhật có các đỉnh nằm trên các đường tiệm cận và có hai cạnh là hai tiếp tuyến của hyberbol, độ dài của hai cạnh này bằng 2b đơn vị độ dài, hai cạnh còn lại song song với trục thực có độ dài bằng 2a đơn vị độ dài. Chú ý rằng b có thể lớn hơn a.

Tính khoảng cách từ một điểm bất kì tới hai tiêu điểm, hiệu hai giá trị này luôn luôn bằng 2a.

Tâm sai được tính bằng công thức

\varepsilon ={\sqrt {1+{\frac {b^{2}}{a^{2}}}}}=\sec \left(\arctan \left({\frac {b}{a}}\right)\right)=\cosh \left(\operatorname {arsinh} \left({\frac {b}{a}}\right)\right)

Nếu c bằng khoảng cách từ tâm cho đến mỗi tiêu điểm, ta có

\varepsilon ={\frac {c}{a}}

trong đó

c={\sqrt {a^{2}+b^{2}}}

.

Khoảng cách c được hiểu là nửa tiêu cự của hyperbol. Khoảng cách giữa hai tiêu điểm (tiêu cự) bằng 2c hay 2aε.

Tiêu điểm của đường hyperbol nằm theo hướng Đông-Tây được xác định bởi công thức:

\left(h\pm c,k\right)

và đối với đường hyperbol Bắc-Nam được xác định bởi công thức

\left(h,k\pm c\right)

.

Đường chuẩn của đường hyperbol nằm theo hướng Đông-Tây được xác định bởi công thức

x=h\pm a\;\cos \left(\arctan \left({\frac {b}{a}}\right)\right)

và đối với đường hyperbol nằm theo hướng Bắc-Nam được xác định bởi công thức

y=k\pm a\;\cos \left(\arctan \left({\frac {b}{a}}\right)\right)

.

Hình hyperbol đều

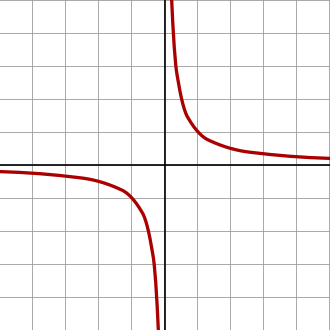
Đối với đường hyperbol đều có trục tọa song song với các đường tiệm cận:

(x-h)(y-k)=c\,

Ví dụ đơn giản nhất của hình hyperbol đều

y={\frac {m}{x}}\,

.

Cực của đường hyperbol

Hình hyperbol nằm theo hướng đông-tây:

r^{2}=a\sec 2\theta \,

Hình hyperbol nằm theo hướng bắc-nam:

r^{2}=-a\sec 2\theta \,

Hình hyperbol nằm theo hướng Đông Bắc-Tây Nam:

r^{2}=a\csc 2\theta \,

Hình hyperbol nằm theo hướng Tây Bắc-Đông Nam

r^{2}=-a\csc 2\theta \,

Hàm số

Hình hyperbol nằm theo hướng Đông-Tây

{\begin{matrix}x=a\sec t+h\\y=b\tan t+k\\\end{matrix}}\qquad \mathrm {or} \qquad {\begin{matrix}x=\pm a\cosh t+h\\y=b\sinh t+k\\\end{matrix}}

Hình hyperbol nằm theo hướng Bắc-Nam:

{\begin{matrix}x=a\tan t+h\\y=b\sec t+k\\\end{matrix}}\qquad \mathrm {or} \qquad {\begin{matrix}x=a\sinh t+h\\y=\pm b\cosh t+k\\\end{matrix}}

Trong công thức (h,k) là tọa độ tâm của hyperbol, a bằng nửa độ dài trục thực, và b bằng nửa độ dài trục ảo.

Hyperbol chữ nhật

Hyperbol chữ nhật, hyperbol đều, hoặc hyperbol vuông là một hyperbol với hai đường tiệm cận vuông góc.^[1]

Phương trình của Hyperbol chữ nhật trong hệ trục tọa độ song song với hai đường tiệm cận:

(x-h)(y-k)=m\,\,\,

.

Phương trình tối giản của hyperbol chữ nhật có dạng sau đây:

y={\frac {m}{x}}\,

Một conic ngoại tiếp đi qua trực tâm của một tam giác là một hyperbol chữ nhật.^[2]

Định lý Feuerbach phát biểu rằng nếu một hyperbol chữ nhật đi qua ba điểm A,B,C thì tâm của hyperbol này nằm trên đường tròn chín điểm của tam giác ABC.

Một hyperbol chữ nhật đi qua ba điểm A,B,C và cắt đường tròn ngoại tiếp tam giác ABC tại T thì tâm của hyperbol này là trung điểm của đoạn thẳng nối trực tâm tam giác ABC và T.^[3]

Trong tam giác có ba đường hyperbol chữ nhật nổi tiếng là hyperbol Kiepert, hyperbol Jerabek và hyperbol Feuerbach.