Mômen lưỡng cực điện

Bài viết về
Điện từ học
Điện Từ học Lịch sử Giáo trình
Tĩnh điện Chất cách điện Chất dẫn điện Cảm ứng tĩnh điện Điện ma sát Điện thông Điện thế Điện trường Điện tích Định luật Coulomb Định luật Gauss Độ điện thẩm Mômen lưỡng cực điện Mật độ phân cực Mật độ điện tích Phóng tĩnh điện Thế năng điện
Tĩnh từ Định luật Ampère Định luật Biot–Savart Định luật Gauss cho từ trường Độ từ thẩm Lực từ động Mômen lưỡng cực từ Quy tắc bàn tay phải Từ hóa Từ thông Từ thế vectơ Từ thế vô hướng Từ trường
Điện động Bức xạ điện từ Cảm ứng điện từ Dòng điện Foucault Dòng điện dịch chuyển Định luật Faraday Định luật Lenz Lực Lorentz Mô tả toán học của trường điện từ Phương trình Jefimenko Phương trình London Phương trình Maxwell Tenxơ ứng suất Maxwell Thế Liénard–Wiechert Trường điện từ Vectơ Poynting Xung điện từ
Mạch điện Bộ cộng hưởng Dòng điện Dòng điện một chiều Dòng điện xoay chiều Điện dung Điện phân Điện trở Định luật Ohm Gia nhiệt Joule Hiện tượng tự cảm Hiệu điện thế Lực điện động Mạch nối tiếp Mạch song song Mật độ dòng điện Ống dẫn sóng điện từ Trở kháng
Phát biểu hiệp phương sai Tenxơ điện từ (tenxơ ứng suất–năng lượng) Dòng bốn chiều Thế điện từ bốn chiều
Các nhà khoa học Ampère Biot Coulomb Davy Einstein Faraday Fizeau Gauss Heaviside Henry Hertz Joule Lenz Lorentz Maxwell Ørsted Ohm Ritchie Savart Singer Tesla Volta Weber

Trong vật lý, moment lưỡng cực điện là một đại lượng đo về sự tách biệt của các điện tích dương và âm trong một hệ hạt điện tích. Các đơn vị SI là Coulomb nhân mét (C.m). Bài viết này chỉ giới hạn trong các hiện tượng tĩnh điện và không mô tả thời gian hay phân cực năng lượng. Độ lớn của moment lưỡng cực điện chính là cường độ điện trường E.

Khái niệm điện tích

Hình động cho thấy điện trường của một lưỡng cực điện

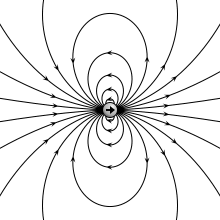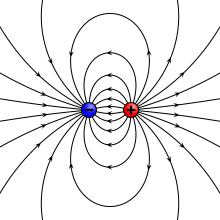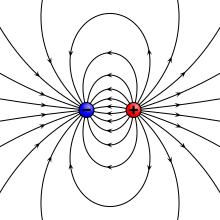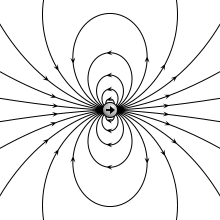
Trong trường hợp đơn giản của hai điện tích điểm, với một điện tích q = +1 và cái còn lại là điện tích q = -1, mômen lưỡng cực điện p là:

$\mathbf {p} =q\mathbf {d}$

trong đó d là các vector chuyển dấu từ các điện tích âm sang điện tích dương. Như vậy, momen lưỡng cực điện từ điện tích âm sang điện tích dương. Một lý tưởng hóa của hệ thống hai điện tích này là lưỡng cực điện gồm hai điện tích vô cùng nhỏ tách ra, nhưng với một hữu hạn p.

Mô men lực

Electric p lưỡng cực và mô-men xoắn τ của nó trong một trường E

Một vật có một moment lưỡng cực điện là đối tượng của một τ - mô-men xoắn khi được đặt trong một trường điện từ. Các mô-men xoắn có xu hướng sắp xếp các lưỡng cực trong một trường. Một lưỡng cực song song với một điện trường có năng lượng thấp hơn so với momen lưỡng cực điện tạo thành một góc với nó. Đối với một không gian có điện trường E, mô-men xoắn được cho bởi công thức :

${\boldsymbol {\tau }}=\mathbf {p} \times \mathbf {E} ,$

trong đó p là mômen lưỡng cực điện, × là tích có hướng giữa các vector.

Biểu diễn trong trường hợp tổng quát

Một cách tổng quát hơn, về sự phân bố điện tích trên một thể tích bị hạn chế, nó biểu thị tương tự cho mômen lưỡng cực điện là:

$\mathbf {p} (\mathbf {r} )=\iiint _{V}\rho (\mathbf {r} _{0})(\mathbf {r} _{0}-\mathbf {r} )\cdot d^{3}\mathbf {r} _{0},$

trong đó r là một điểm có điện tích và d³r₀ là vi phân cấp 3 của vị trí đầu có điện tích nằm trên thể tích V. Mômen lưỡng cực điện còn được thể hiện qua hàm delta Dirac như sau:

$\rho (\mathbf {r} )=\sum _{i=1}^{N}q_{i}\delta (\mathbf {r} -\mathbf {r} _{i}),$

trong đó mỗi r_i là một vector từ một số điểm tham chiếu đến các điện tích q_i được thay vào công thức tích phân như trên:

$\mathbf {p} (\mathbf {r} )=\sum _{i=1}^{N}q_{i}\iiint _{V}\delta (\mathbf {r} _{0}-\mathbf {r} _{i})(\mathbf {r} _{0}-\mathbf {r} )\cdot d^{3}\mathbf {r} _{0}=\sum _{i=1}^{N}q_{i}(\mathbf {r} _{i}-\mathbf {r} ).$

Biểu thức này tương đương với các biểu thức trước đó trong trường hợp điện tích trung hòa và N = 2. Đối với hai điện tích trái dấu nhau, nó thể hiện điện tích dương trong các cặp điện tích như r⁺ và điện tích âm như r^-:

$\mathbf {p} (\mathbf {r} )=q_{1}(\mathbf {r} _{1}-\mathbf {r} )+q_{2}(\mathbf {r} _{2}-\mathbf {r} )=q(\mathbf {r} ^{+}-\mathbf {r} )-q(\mathbf {r} ^{-}-\mathbf {r} )=q(\mathbf {r^{+}-r^{-}} )=q\mathbf {d} ,$

cho thấy rằng vector mômen lưỡng cực điện có nguồn từ điện tích âm đến dương vì các vector của một điểm có hướng từ nguồn cho đến điểm đó. Momen lưỡng cực điện dễ thấy nhất khi một hệ điểm có tất cả các hạt mang điện trung hòa; Ví dụ, một cặp điện đối dấu, hoặc một dây dẫn trung tính trong một điện trường đồng nhất. Đối với một hệ điểm không có điện tích, hình dung như là một dãy các điện tích kết nối với nhau, các mối quan hệ cho momen lưỡng cực điện là:

${\begin{aligned}\mathbf {p} (\mathbf {r} )&=\sum _{i=1}^{N}\,\iiint \limits _{V}q_{i}[\delta (\mathbf {r_{0}} -(\mathbf {r} _{i}+\mathbf {d} _{i}))-\delta (\mathbf {r_{0}} -\mathbf {r} _{i})]\,(\mathbf {r} _{0}-\mathbf {r} )\ d^{3}\mathbf {r} _{0}\\&=\sum _{i=1}^{N}\,q_{i}\,[\mathbf {r} _{i}+\mathbf {d} _{i}-\mathbf {r} -(\mathbf {r} _{i}-\mathbf {r} )]\\&=\sum _{i=1}^{N}q_{i}\mathbf {d} _{i}=\sum _{i=1}^{N}\mathbf {p} _{i}\,\end{aligned}}$

đó là vector tổng của những mômen lưỡng cực điện duy nhất của các cặp điện tích trung hòa. (Bởi vì toàn bộ hạt mang điện trung hòa, các moment lưỡng cực điện độc lập với vị trí r.) Như vậy, giá trị của p là độc lập với vị trí ta muốn xét tới, qui ước toàn bộ điện tích của hệ điểm là bằng 0.

Điện thế và điện trường bởi lưỡng cực điện

Lưỡng cực điện lý tưởng gồm hai điện tích trái dấu nhau với sự phân li vô cùng nhỏ. Điện thế và điện trường lý tưởng được tìm thấy bên cạnh là một trường hợp giới hạn của một ví dụ về hai điện tích trái dấu phân li khi khoảng cách giữa chúng tiến đến không. Hai điện tích trái dấu ở gần nhau có thể tạo ra điện thế và có biểu thức:

$\phi (\mathbf {r} )={\frac {q}{4\pi \varepsilon _{0}|\mathbf {r} -\mathbf {r} ^{+}|}}-{\frac {q}{4\pi \varepsilon _{0}|\mathbf {r} -\mathbf {r} ^{-}|}},$

Vector vị trí R của trung điểm lưỡng cực liên quan đến khối lượng (giả sử chúng bằng nhau), ${\hat {\mathbf {R} }}$ là vector đơn vị trùng hướng với R được cho bởi biểu thức:

$\mathbf {R} =\mathbf {r} -{\frac {\mathbf {r} ^{+}+\mathbf {r} ^{-}}{2}},{\hat {\mathbf {R} }}={\frac {\mathbf {R} }{R}},$

Dùng khai triển Taylor ta được :

$\phi (\mathbf {R} )={\frac {1}{4\pi \varepsilon _{0}}}{\frac {q\mathbf {d} \cdot {\hat {\mathbf {R} }}}{R^{2}}}+{\mathcal {O}}\left({\frac {d^{2}}{R^{2}}}\right)\approx {\frac {1}{4\pi \varepsilon _{0}}}{\frac {\mathbf {p} \cdot \mathbf {R} }{R^{3}}},$

Điện thế bởi lưỡng cực điện cũng được biểu diễn như sau :

$\phi (\mathbf {R} )=-\mathbf {p} \cdot {\vec {\mbox{grad }}}{\frac {1}{4\pi \varepsilon _{0}}}R,$

với grad là toán tử gradient. Điện trường của lưỡng cực điện là âm gradient của điện thế dẫn tới :

$\mathbf {E} (\mathbf {R} )={\frac {3(\mathbf {p} \cdot {\hat {\mathbf {R} }})-\mathbf {p} }{4\pi \varepsilon _{0}R^{3}}}.$

Do đó, mặc dù hai điện tích trái dấu gần nhau không có vẻ là lưỡng cực điện lý tưởng (vì điện thế của chúng ở khoảng cách ngắn không tương tự điện thế bởi một lưỡng cực điện lý tưởng), ở vị trí xem xét lớn hơn nhiều so với khoảng cách phân li, mômen lưỡng cực xuất hiện rõ rệt trong biểu thức điện trường và điện thế.

Xem thêm

• Mômen lưỡng cực từ
• Phương trình Maxwell
• Mật độ phân cực
• Khai triển Taylor
• Gradient
• Toán tử div
• Rot (toán tử)

Liên kết ngoài

• Electric Dipole Moment – from Eric Weisstein's World of Physics
• Electrostatic Dipole Multiphysics Model o