Chuyển động tròn
Trong vật lý, chuyển động tròn là chuyển động quay của một chất điểm trên một vòng tròn: một cung tròn hoặc quỹ đạo tròn. Nó có thể là một chuyển động đều với vận tốc góc không đổi, hoặc chuyển động không đều với vận tốc góc thay đổi theo thời gian. Các phương trình mô tả chuyển động tròn của một vật không có kích thước hình học, đúng hơn là chuyển động của một điểm giả định trên một mặt phẳng. Trong thực tế, khối tâm của vật đang xét có thể được coi là chuyển động tròn.
Ví dụ chuyển động tròn của một vệ tinh nhân tạo bay quanh Trái Đất theo một quỹ đạo địa tĩnh, một hòn đá được cột với một sợi dây và quay tròn (ném tạ), một chiếc xe đua chạy qua một đường cong trong một đường đua, một electron chuyển động vuông góc với một từ trường đều, và bánh răng quay trong một máy cơ khí.
Chuyển động tròn là không đều ngay cả khi vận tốc góc ω không đổi, bởi vì vector vận tốc v của điểm đang xét liên tục đổi hướng. Sự thay đổi hướng của vận tốc liên quan đến gia tốc gây ra do lực hướng tâm kéo vật di chuyển về phía tâm của quỹ đạo tròn. Nếu không có gia tốc này, đối tượng sẽ di chuyển trên một đường thẳng theo các định luật của Newton về chuyển động.
Mô tả chuyển động tròn bằng hệ tọa độ cực[sửa | sửa mã nguồn]
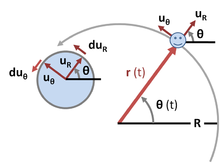
Trong chuyển động tròn, vật di chuyển trên một đường cong có thể miêu tả bằng hệ tọa độ cực với 1 trục R cố định tính từ tâm của quỹ đạo, góc θ (t) thay đổi so với trục gốc R. Xem hình 3: vector là một vector bán kính từ trục đến vị trí vật:
với là vector đơn vị song song cùng hướng với vector bán kính tại thời điểm t và chỉ vị trí so với trục gốc. Vận tốc là đạo hàm theo thời gian của độ dịch chuyển:
Biểu diễn bằng số phức[sửa | sửa mã nguồn]
Chuyển động tròn có thể biểu diễn bằng số phức. Với trục thực và trục ảo , vị trí của vật chuyển động tròn đều có thể biểu diễn bằng vector số phức :
với là số ảo đơn vị, và
là góc của vector phức tạo với trục thực và là 1 hàm số theo biến t. Vì bán kính là hằng số:
dấu chấm (đạo hàm) cho thấy sự khác biệt về thời gian. Với ký hiệu này, vận tốc trở thành:
và gia tốc trở thành:
Chuyển động tròn đều[sửa | sửa mã nguồn]

Phương trình của chuyển động tròn với bán kính quỹ đạo r, chu vi C = 2π r. Chu kỳ T, vận tốc góc ω:
Góc θ quét trên mặt phẳng quỹ đạo trong một thời gian t:
Vận tốc[sửa | sửa mã nguồn]
Bởi vì vận tốc v là tiếp tuyến với đường tròn, và không có hai vận tốc điểm trong cùng một hướng. Mặc dù độ lớn của vận tốc không đổi nhưng hướng của nó luôn luôn thay đổi. Sự thay đổi hướng của vận tốc này được gây ra bởi một gia tốc có độ lớn cũng không đổi, nhưng có hướng cũng luôn luôn thay đổi. Gia tốc luôn hướng vào tâm quỹ đạo và vuông góc với vận tốc. Gia tốc này được gọi là gia tốc hướng tâm.
Với quỹ đạo có bán kính r, khi vật di chuyển quét 1 góc θ, thì quãng đường dài di chuyển của vật trên quỹ đạo sẽ là s = rθ. Do đó, vận tốc là:
- ,
vì là chuyển động tròn đều nên vận tốc góc ω không đổi, cho nên vận tốc v cũng không đổi.
Gia tốc hướng tâm[sửa | sửa mã nguồn]
Vòng tròn bên trái trong hình 1 là quỹ đạo cho thấy các vectơ vận tốc tại 2 điểm liền kề. Vòng tròn bên phải hình là hai vận tốc di chuyển để trùng vào nhau (dt → 0). Bởi vì vận tốc góc không đổi, vectơ vận tốc cũng quét ra một vòng tròn tương tự. Đối với một góc quét dθ = ωdt sự biến đổi của v sẽ là một vector vuông góc với v và có độ lớn bằng vdθ, do đó độ lớn của gia tốc được tính bởi phương trình:
Các vector[sửa | sửa mã nguồn]

Các mối quan hệ vector được thể hiện trong hình 2. Trục quay được hiển thị như là một vector Ω vuông góc với mặt phẳng quỹ đạo và có độ lớn ω = dθ / dt. Chiều của vector Ω tuân theo quy tắc bàn tay phải. Vector vận tốc được tính theo phép tích vector:
là một vector vuông góc với cả hai vector Ω và r (t), tiếp tuyến với quỹ đạo và có độ lớn bằng ω r. Tương tự, vector gia tốc được tính theo công thức:
là một vector vuông góc với cả hai vector Ω và v (t) với độ lớn bằng ω |v| = ω2 r và ngược hướng với vector r (t).[1]
Quan hệ với dao động điều hòa[sửa | sửa mã nguồn]
Hình chiếu của 1 điểm chuyển động tròn đều xuống một trục nằm trong mặt quẳng quỹ đạo là một dao động điều hòa. Ngược lại, bất kỳ một dao động điều hòa nào cũng có thể biểu diễn bằng 1 vector có mũi chuyển động tròn đều với vận tốc góc ω=2π/T trong đó T là chu kỳ của dao động điều hòa, độ lớn vector là biên độ dao động, góc tạo với trục tọa độ là pha ban đầu.
Chuyển động tròn biến đổi đều[sửa | sửa mã nguồn]

a trong chuyển động biến đổi đều là tổng của 2 vector gia tốc pháp tuyến hướng tâm aR và gia tốc tiếp tuyến aθChuyển động tròn biến đổi đều là chuyển động của một chất điểm trên 1 quỹ đạo hình tròn có gia tốc tiếp tuyến aθ luôn luôn không đổi, chuyển động có thể là nhanh dần đều hoặc chậm dần đều. Một số ví dụ của chuyển động tròn biến đổi đều như một tàu lượn, một con lắc đơn, hay một chiếc xe hơi chay trên một ngọn đồi hình cung tròn.
Gia tốc hướng tâm hay còn gọi là gia tốc pháp tuyến aR có giá trị bằng , với là độ lớn của vận tốc tại điểm đang xét: v = v0 + , với aθtv0 là vận tốc ban đầu của chất điểm tại t0=0.[2]
Vector gia tốc tiếp tuyến aθ, có phương trùng với tiếp tuyến của quỹ đạo tròn tại điểm đang xét và có độ lớn là đạo hàm bậc nhất của vận tốc theo thời gian: .
Chính gia tốc tiếp tuyến làm thay đổi vận tốc chất điểm. Nguyên nhân làm xuất hiện gia tốc này là do chất điểm chịu ảnh hưởng bởi các ngoại lực tác động vào, ví dụ như lực ma sát hoặc trọng lực.
Gia tốc toàn phần tại 1 điểm có giá trị:
Góc lệch μ tạo thành giữa a với aθ[3]:
Chú thích[sửa | sửa mã nguồn]
- ^ Knudsen, Jens M.; Hjorth, Poul G. (2000). Elements of Newtonian mechanics: including nonlinear dynamics (ấn bản 3). Springer. tr. 96. ISBN 3-540-67652-X., Chapter 5 page 96
- ^ M. X. Targ & Phạm Huyền (dịch) (1983). Giáo trình giản yếu cơ học lý thuyết. <<MIR>> Maxcơva, Nhà xuất bản Đại học và trung học chuyên nghiệp Hà Nội. tr. 159.Quản lý CS1: sử dụng tham số tác giả (liên kết)
- ^ M. X. Targ & Phạm Huyền (dịch) (1983). Giáo trình giản yếu cơ học lý thuyết. <<MIR>> Maxcơva, Nhà xuất bản Đại học và trung học chuyên nghiệp Hà Nội. tr. 156-157.Quản lý CS1: sử dụng tham số tác giả (liên kết)
Liên kết ngoài[sửa | sửa mã nguồn]
- Circular Motion Lưu trữ 2010-12-14 tại Wayback Machine - một chương sách giáo khoa trực tuyến.
- Circular Motion Lecture Lưu trữ 2010-01-17 tại Wayback Machine - một video bài giảng trên CM.
































