Định lý Thales

Định lý Thales, hay định lý Thalès, định lý Talet, là một định lý quan trọng trong hình học sơ cấp, được đặt theo tên nhà toán học người Hy Lạp Thales. Mặc dù định lý Thales đã được người Babylon và Ai Cập cổ đại biết đến, bằng chứng đầu tiên về định lý này xuất hiện trong cuốn Cơ sở của Euclid.

Định lý Thales trong tam giác[sửa | sửa mã nguồn]

Định lý Thales được phát biểu như sau:^[1]

Nếu 1 đường thẳng song song với 1 cạnh của tam giác đó và cắt 2 cạnh còn lại thì nó định ra trên 2 cạnh đó những đoạn thẳng tương ứng tỷ lệ.

Tại hình vẽ bên nếu có tam giác ABC, d cắt AB tại D, cắt AC tại E, song song với BC, như vậy theo định lý Thales, có:

{\frac {\mbox{AD}}{\mbox{AB}}}={\frac {\mbox{AE}}{\mbox{AC}}}

và

{\frac {\mbox{AD}}{\mbox{DB}}}={\frac {\mbox{AE}}{\mbox{EC}}}

và

{\frac {\mbox{DB}}{\mbox{AB}}}={\frac {\mbox{EC}}{\mbox{AC}}}

.

Định lý Thales đảo[sửa | sửa mã nguồn]

Định lý Thales có tính hai chiều. Định lý Thales đảo được phát biểu như sau:^[2]

Nếu một đường thẳng cắt hai cạnh của tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỷ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Tại hình vẽ bên nếu có tam giác ABC; ${\frac {\mbox{AD}}{\mbox{AB}}}={\frac {\mbox{AE}}{\mbox{AC}}}$ hoặc ${\frac {\mbox{AD}}{\mbox{DB}}}={\frac {\mbox{AE}}{\mbox{EC}}}$ hoặc ${\frac {\mbox{DB}}{\mbox{AB}}}={\frac {\mbox{EC}}{\mbox{AC}}}$ , như vậy theo định lý Thales đảo, có: DE song song với BC (DE // BC).

Hệ quả của định lý Thales – định lý Thales mở rộng[sửa | sửa mã nguồn]

Hệ quả 1[sửa | sửa mã nguồn]

Hệ quả 1 của định lý Thales được phát biểu như sau:

Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác có ba cạnh tỷ lệ với ba cạnh của tam giác đã cho.

Hệ quả 2[sửa | sửa mã nguồn]

Hệ quả 2 của định lý Thales được phát biểu như sau:

Có một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới đồng dạng với tam giác đã cho.

Hệ quả 3 – Thales mở rộng[sửa | sửa mã nguồn]

Hệ quả 3 – Thales mở rộng được phát biểu như sau:

Ba đường thẳng đồng quy thì chắn trên hai đường thẳng song song các cặp đoạn thẳng tỷ lệ.

Định lý Thales trong hình thang[sửa | sửa mã nguồn]

Định lý Thales đối với hình thang như sau:

Nếu có một đường thẳng song song với 2 cạnh đáy của hình thang và cắt 2 cạnh bên của hình thì nó định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỷ lệ.

Định lý Thales trong không gian[sửa | sửa mã nguồn]

Ba mặt phẳng song song chắn trên 2 đường thẳng những đoạn thẳng tỷ lệ.

Định lý đảo[sửa | sửa mã nguồn]

Cho 2 đường thẳng $d_{1}$ và $d_{2}$ chéo nhau. Lấy các điểm $A_{1}$ , $B_{1}$ , $C_{1}$ $\in (d_{1})$ và $A_{2}$ , $B_{2}$ , $C_{2}$ $\in (d_{2})$ sao cho ${\frac {A_{1}B_{1}}{B_{1}C_{1}}}={\frac {A_{2}B_{2}}{B_{2}C_{2}}}$ . Khi đó các đường thẳng $A_{1}A_{2}$ , $B_{1}B_{2}$ , $C_{1}C_{2}$ cùng song song với một mặt phẳng.

Các khái niệm liên quan[sửa | sửa mã nguồn]

Đồng dạng và tam giác đồng dạng[sửa | sửa mã nguồn]

Định lý Thales có liên quan chặt chẽ đến khái niệm đồng dạng. Định lý Thales có thể được dùng để chứng minh tam giác đồng dạng, cũng như có thể dùng tam giác đồng dạng để chứng minh định lý Thales.

Phép nhân vô hướng trong không gian vectơ[sửa | sửa mã nguồn]

Trong không gian định chuẩn, các tiên đề liên quan đến phép nhân vô hướng (đặc biệt là $\lambda \cdot ({\vec {a}}+{\vec {b}})=\lambda \cdot {\vec {a}}+\lambda \cdot {\vec {b}}$ và $\|\lambda {\vec {a}}\|=|\lambda |\cdot \ \|{\vec {a}}\|$ ) đã giúp khẳng định tính đúng đắn của định lý Thales. Trong hình, ta có ${\frac {\|\lambda \cdot {\vec {a}}\|}{\|{\vec {a}}\|}}={\frac {\|\lambda \cdot {\vec {b}}\|}{\|{\vec {b}}\|}}={\frac {\|\lambda \cdot ({\vec {a}}+{\vec {b}})\|}{\|{\vec {a}}+{\vec {b}}\|}}=|\lambda |$ .

Ứng dụng[sửa | sửa mã nguồn]

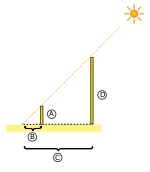
Định lý Thales được áp dụng rất nhiều vào thực tiễn. Đơn giản nhất là công việc đo đạc kích thước của một vật lớn mà con người không thể đo trực tiếp. Một số ví dụ về ứng dụng của định lý này bao gồm: đo khoảng cách giữa hai bờ sông, dùng bóng Mặt Trời và định lý Thales để đo chiều cao vật,...