Hằng số vũ trụ

Hằng số vũ trụ

Hằng số vũ trụ ban đầu do Albert Einstein đưa ra vào năm 1917 khi ông coi nó là lực đẩy nhằm giữ cho Vũ trụ trong trạng thái cân bằng tĩnh. Trong ngành vũ trụ học hiện đại, nó là ứng cử viên hàng đầu cho năng lượng tối, loại gây ra sự giãn nở gia tốc của vũ trụ ngày nay.

Trong phạm vi của ngành vũ trụ học, hằng số vũ trụ (hay hằng số vũ trụ học) là dạng mật độ năng lượng đồng nhất gây ra sự giãn nở gia tốc của vũ trụ.

Nó được đề xuất từ lúc mới hình thành phát triển của thuyết tương đối rộng để có thể miêu tả một nghiệm vũ trụ tĩnh suy ra từ phương trình trường Einstein, nhưng sau đó các nhà thiên văn từ bỏ nó khi các quan sát thực nghiệm trong thập niên 1930 cho thấy vũ trụ đang giãn nở. Hiện tại, hằng số vũ trụ học được khôi phục trở lại nhằm giải thích kết quả quan sát vũ trụ đang giãn nở gia tốc. Hằng số vũ trụ học là cách giải thích đơn giản nhất cho năng lượng tối, nguyên nhân chưa được hiểu rõ gây ra sự giãn nở gia tốc này. Vật lý lượng tử cũng tiên đoán sự tồn tại của nó dưới dạng năng lượng chân không, mặc dù độ lớn tính toán từ lý thuyết lượng tử không khớp với giá trị đo được của vật lý vũ trụ học.

Lịch sử

Hằng số vũ trụ xuất hiện lần đầu tiên trong một bài báo năm 1917 của Einstein có tiêu đề "Những khía cạnh vũ trụ học của thuyết tương đối tổng quát"., trong đó ông giới thiệu hằng số vào lý thuyết tương đối tổng quát nhằm thu được nghiệm ổn định của vũ trụ chống lại sức hút của hấp dẫn:

"Số hạng này chỉ cần thiết cho mục đích tạo ra sự phân bố gần tĩnh tại của vật chất, như thực tế cho thấy các ngôi sao có vận tốc chuyển động khá nhỏ"

Ở giai đoạn này, các quan sát thiên văn tập trung vào các sao trong Ngân Hà do bị giới hạn bởi độ phân giải của kính thiên văn, do đó thực sự có chứng cứ quan sát cho thấy giả thiết vũ trụ tĩnh tại là đúng. Mục đích của Einstein là nhằm mô tả mô hình vũ trụ thỏa mãn nguyên lý Mach về tính tương đối của quán tính (về thảo luận lịch sử xem Pais 1982), và ông xây dựng một vũ trụ có kích thước hữu hạn, ổn định so với lực hấp dẫn hút mọi sao về phía nhau. Mô hình này nhanh chóng gặp những khó khăn, khi ngay sau đó nhà thiên văn học de Sitter (1917) đã chứng tỏ tồn tại một nghiệm vũ trụ mà trống rỗng từ phương trình trường Einstein (cho phép quán tính liên hệ tương đối với không gian trống rỗng vật chất) và nhà vật lý thiên văn Alexander Friedman năm 1922 đã thu được một nghiệm từ phương trình trường Einstein miêu tả vũ trụ đang giãn nở. Những kết quả này đưa các nhà thiên văn Friedmann, Georges Lemaître tới tiên đoán vũ trụ phải đang giãn nở hoặc co lại, một hệ quả bất ngờ từ thuyết tương đối rộng mà sau này đã được phát hiện bằng thực nghiệm. Khi Edwin Hubble thực hiện quan sát các "tinh vân" và đo khoảng cách tới chúng, ông nhận thấy các tinh vân càng ở xa thì có dịch chuyển đỏ càng lớn và vận tốc lùi xa của chúng tỷ lệ với khoảng cách từ chúng tới Trái Đất. Khám phá về vũ trụ đang giãn nở khiến Einstein cuối cùng hoàn toàn từ bỏ hằng số vũ trụ khi ông không thấy nó phải cần thiết nữa.

Trong những năm sau đó, hằng số vũ trụ xuất hiện trở lại khi những kết quả quan sát mới dường như đòi hỏi phải có nó, nhưng ý nghĩa vật lý của nó được giải thích theo một cách khác. Cho tới đầu thập kỷ 1990 có những dấu hiệu tinh tế cho thấy các nhà vũ trụ học lại một lần nữa phải cần tới hằng số này. Dường như tuổi của vũ trụ lại ít hơn những ngôi sao già nhất trong nó, một đặc điểm nghịch lý nếu vũ trụ hiện tại đang trong giai đoạn giãn nở gia tốc. Số lượng các thiên hà trong một thể tích góc khối ở độ dịch chuyển đỏ cao lớn hơn số lượng thiên hà ước lượng trong vũ trụ đang giãn nở giảm dần. Các lập luận từ lý thuyết lạm phát và những kết quả quan sát về sau từ bức xạ nền vi sóng vũ trụ chứng tỏ hình học của vũ trụ có dạng phẳng, nhưng lại có một điều khó giải thích khác đó là khi quan sát trên cấu trúc lớn thì mật độ vật chất lại không đủ để vũ trụ có dạng phẳng - và năng lượng chân không có thể bù vào sự thiếu hụt này.

Ước lượng sự phân bố của vật chất và năng lượng trong vũ trụ.

Các nhà vũ trụ học trở lên tin tưởng hơn vào điều này khi hai đội các nhà thiên văn đã phát hiện ra vũ trụ giãn nở gia tốc vào năm 1998/1999. Đội siêu tân tinh Z-Cao và dự án Vũ trụ siêu tân tinh đều khám phá ra các siêu tân tinh có độ dịch chuyển đỏ cao mờ hơn so với dự kiến trong mô hình vũ trụ giãn nở giảm tốc và sự khác nhau này có thể giải thích dựa trên hằng số vũ trụ học với độ lớn phù hợp cần thiết để vũ trụ là phẳng.

Đây quả là một sự trùng khớp kỳ lạ giữa lý thuyết và quan sát. Kể từ đó những tàu không gian quan sát đã xác nhận với độ chính xác cao hơn cho sự cần thiết của năng lượng tối, nhưng bản chất của năng lượng tối vẫn đang là câu hỏi mở chưa có giải đáp. Cho tới 2015 các tính chất đo được của năng lượng tối vẫn tương thích với mô hình về một hằng số vũ trụ học. Tuy nhiên, đang có những nỗ lực quan sát để kiểm tra đây là cách giải thích đúng đắn cho sự giãn nở gia tốc hay liệu có một mô hình khác cho năng lượng tối, có lẽ sẽ có thứ thay đổi theo thời gian hoặc lý thuyết về hấp dẫn lượng tử sẽ giải thích được sự giãn nở mà chúng ta quan sát được.

Sai lầm lớn nhất

Trong tự thuật của mình, My World Line, George Gamow viết ông đã từng hỏi Einstein về vấn đề khi đưa hằng số vũ trụ học vào phương trình trường của ông:

"Lâu về sau, khi tôi đang thảo luận với Einstein về vấn đề hằng số vũ trụ học, tôi nhớ ông cho rằng việc giới thiệu ra hằng số vũ trụ học là một sai lầm lớn nhất của đời ông. "

Mặc dù đây là một trong những danh ngôn thường được nhắc đến nhiều trong ngành vũ trụ học, nhưng gần đây các nhà nghiên cứu lịch sử vật lý học nhận thấy Einstein chỉ nhắc tới "sai lầm cơ bản" của ông về hằng số vũ trụ học, trong khi ở tự thuật của Gamow, Gamow đã viết thành "sai lầm lớn nhất". Họ cũng không tìm thấy trong tài liệu gốc nào do chính Einstein viết về sai lầm lớn nhất này.

Hằng số vũ trụ học trong vật lý

Để khám phá bản chất sâu hơn của Vũ trụ, chúng ta phải sử dụng ngôn ngữ toán học trong thuyết tương đối rộng của Einstein nhằm liên hệ hình học của không thời gian (thể hiện bằng tenxơ mêtric, g_μν) với lượng năng lượng trong Vũ trụ, (thể hiện bằng tenxơ ứng suất–năng lượng, T_μν).

Phương trình trường Einstein

Một trong những phát hiện quan trọng nhất của Einstein đó là sự phân bố của vật chất và năng lượng xác định lên hình học của không thời gian, mà được miêu tả trong phương trình trường của ông

$R_{\mu \nu }-{\frac {1}{2}}R\,g_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }$

(1)

trong đó:

• R_μν: tenxơ Ricci
• R: vô hướng Ricci
• g_μν: tenxơ mêtric
• c: vận tốc ánh sáng trong chân không
• G: hằng số hấp dẫn (giống như hằng số hấp dẫn trong định luật hấp dẫn của Newton)
• T_μν: tenxơ năng lượng-xung lượng

R và g gắn liến với cấu trúc của không-thời gian, T gắn liền với vật chất và năng lượng, G và c phụ thuộc vào hệ đơn vị đo lường.

Mặc dù đây là dạng đơn giản nhất của phương trình, ta vẫn còn có thể tự do thêm vào một số hạng hằng số trong phương trình mà vẫn có thể đảm bảo định luật bảo toàn năng lượng toàn phần (hay đạo hàm hiệp biến của hai vế phương trình bằng 0). "Hằng số vũ trụ học" mà Einstein thêm vào với mục đích thu được mô hình vũ trụ tĩnh tại, và ông ký hiệu nó là Λ.

$R_{\mu \nu }-{\frac {1}{2}}R\,g_{\mu \nu }+\Lambda \,g_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }$

(2)

Năng lượng chân không

Năng lượng chân không xuất hiện một cách tự nhiên trong cơ học lượng tử là do nguyên lý bất định. Trong vật lý hạt, chân không được coi như trạng thái nền - trạng thái có cấu hình năng lượng thấp nhất. Nguyên lý bất định không cho phép trạng thái năng lượng có giá trị thấp nhất bằng 0, ngay cả trong chân không (bởi vì các hạt ảo luôn được tạo ra và hủy lẫn nhau). Vì trong thuyết tương đối rộng mọi dạng năng lượng đều hình thành lên năng lượng hấp dẫn, trạng thái năng lượng chân không nền này ảnh hưởng tới động lực giãn nở của vũ trụ.

Năng lượng chân không không thể là một quá trình có sự tiêu tán nào như dẫn nhiệt hay tính nhớt, do đó nó có thể được coi là một dạng chất lỏng lý tưởng, với tenxơ năng lượng-xung lượng có dạng

$T_{\mu \nu }\,=\left(\rho +{p \over c^{2}}\right)U_{\mu }U_{\nu }+pg_{\mu \nu }$

(3)

với U là trường vectơ vận tốc của chất lỏng, $\rho$ là mật độ khối lượng, p là áp suất đẳng hướng.

Để thỏa mãn tính bất biến Lorentz, năng lượng chân cũng không thể có một hướng chuyển động ưu tiên nào cả. Do vậy số hạng thứ nhất trong tenxơ năng lượng-ứng suất phải bằng 0, hay (đặt c = 1)

${\rho }^{vacuum}=-{p}^{vacuum}$

(4)

mà tương ứng với phương trình trạng thái $w^{vac}={p^{vac} \over {\rho }^{vac}}=-1$ và năng lượng chân không có tenxơ năng lượng-xung lượng bằng

${T_{\mu \nu }}^{vac}\,=p^{vac}g_{\mu \nu }=-{\rho }^{vac}g_{\mu \nu }$

(5)

Sự tương đương giữa hằng số vũ trụ và năng lượng chân không

Có thể tách năng lượng-xung lượng ra thành hai số hạng, một số hạng mô tả năng lượng và vật chất, còn số hạng kia mô tả riêng năng lượng chân không, $T_{\mu \nu }={T}_{\mu \nu }^{matter}+{T}_{\mu \nu }^{vac}$ phương trình Einstein bao gồm năng lượng chân không trở thành:

$R_{\mu \nu }-{\frac {1}{2}}R\,g_{\mu \nu }={8\pi G}({T}_{\mu \nu }^{matter}-{\rho }^{vac}g_{\mu \nu })$

(6)

Mặt khác phương trình trường Einstein khi có sự xuất hiện của hằng số vũ trụ học (2)

$R_{\mu \nu }-{\frac {1}{2}}R\,g_{\mu \nu }+\Lambda \,g_{\mu \nu }={8\pi G}T_{\mu \nu }$

Do vậy hằng số vũ trụ học (xuất hiện ở bên vế cấu trúc hình học không thời gian) về mặt vật lý có vai trò tương đương với năng lượng chân không (xuất hiện ở bên vế tenxơ năng lượng ứng suất vật chất), và có liên hệ:

${\rho }^{vac}={\Lambda \over {8\pi G}}$

(7)

Vũ trụ học

Trong mô hình vũ trụ đồng nhất và đẳng hướng, sự phân bố vật chất và năng lượng trong vũ trụ được mô hình hóa như một chất lỏng lý tưởng, và cấu trúc hình học của nó được miêu tả bẳng mêtric Friedmann–Lemaître–Robertson–Walker (mêtric FLRW) và sự tiến hóa động lực của vũ trụ chi phối bởi phương trình Friedmann. Động lực này ảnh hưởng từ thành phần năng lượng trong Vũ trụ và phương trình trạng thái liên hệ giữa mật độ khối lượng và áp suất $w={p \over {\rho }}$. Hằng số vũ trụ học xuất hiện trong những phương trình này theo cách sau, với a(t) là hệ số tỷ lệ của vũ trụ được chuẩn hóa bằng 1 tại thời điểm hiện tại, $H={{\dot {a}} \over a}$ là hằng số Hubble (dấu chấm trên a thể hiện đạo hàm của nó theo thời gian), và k là độ cong của vũ trụ chuẩn hóa thành +1, 0, và -1 tương ứng với độ cong dương, phẳng, và âm,

$H^{2}={\frac {{\dot {a}}^{2}}{a^{2}}}={\frac {8\pi G}{3}}\rho -{\frac {k}{a^{2}}}+{\frac {\Lambda }{3}}$

(8)

${\frac {\ddot {a}}{a}}=-{\frac {4\pi G}{3}}\left(\rho +3p\right)+{\frac {\Lambda }{3}}$

(9)

Những phương trình này được viết một cách cụ thể hơn khi coi hằng số vũ trụ và độ cong dưới dạng mật độ năng lượng ${\rho }_{\Lambda }={\Lambda \over {8\pi G}}$ và ${\rho }_{k}={-3k \over {8\pi Ga^{2}}}$

Các phương trình (8) và (9) trở thành

$H^{2}={\frac {8\pi G}{3}}\sum _{i}\rho _{i}$

(10)

${\frac {\ddot {a}}{a}}=-{\frac {4\pi G}{3}}\sum _{i}(\rho _{i}+3p_{i})$

(11)

Các thành phần khác nhau có phương trình trạng thái $w_{i}$ khác nhau, mà xác định lên mật độ của chúng thay đổi như thế nào cùng với sự giãn nở của vũ trụ

$\rho _{i}=\rho _{i0}a^{-3(1+w_{i})}$

(12)

Vật chất không gây áp suất có $w=0$, đối với bức xạ có $w={\frac {1}{3}}$, độ cong có $w=-{\frac {1}{3}}$, hằng số vũ trụ có $w=-1$ (chúng ta sử dụng $w_{\Lambda }=-1$ và rút ra được $\rho _{\Lambda }+3p_{\Lambda }=-2\rho _{\Lambda }$ từ phương trình (11))

Mật độ hiện tại của mỗi thành phần, $\rho _{i0}$ thường được biểu diễn bằng tỷ lệ với mật độ giới hạn $\rho _{c}={\frac {3{H_{0}}^{2}}{8\pi G}}$, đó là mật độ đòi hỏi để vũ trụ là phẳng (như được tính toán tại thời điểm hiện tại). Ký hiệu tỷ số này là $\Omega _{i}={\frac {\rho _{i0}}{\rho _{c}}}$ và sử dụng phương trình (12) cho phép viết được

$H^{2}={H_{0}}^{2}\sum _{i}{\frac {\rho _{i}}{\rho _{c}}}={H_{0}}^{2}\sum _{i}\Omega _{i}a^{-3(1+w_{i})}={H_{0}}^{2}(\Omega _{R}a^{-4}+\Omega _{M}a^{-3}+\Omega _{k}a^{-2}+\Omega _{\Lambda })$

(13)

trong đó $\Omega _{R},\Omega _{M},\Omega _{k},\Omega _{\Lambda }$ lần lượt là tỷ số giữa mật độ bức xạ, mật độ vật chất (baryon và tối), mật độ độ cong không gian và mật độ năng lượng tối so với mật độ giới hạn.

Để áp suất sinh công cần phải có một gradien áp suất—một vùng áp suất tương đối cao nằm gần một vùng áp suất tương đối thấp—điều này sẽ là nguyên nhân gây chuyển động từ áp suất cao đến áp suất thấp. Trong một vũ trụ đồng nhất sẽ không có gradien áp suất, vì thế một áp suất dương sẽ không sinh công và không có hiệu ứng giãn nở (không có những vùng áp suất thấp để có thể đẩy vật chất vào vùng đó). Ngược lại, trong thuyết tương đối rộng mọi dạng năng lượng đều tạo ra trường hấp dẫn vì thế áp suất càng lớn càng làm trường hấp dẫn mạnh thêm (lực hấp dẫn trở lên mạnh hơn) (p xuất hiện trong phương trình (9) mà không thể xảy ra như ở thuyết hấp dẫn của Newton). Trong trường hợp năng lượng chân không, ta có $w=-1$ và $p_{\Lambda }=-\rho _{\Lambda }$ hay năng lượng chân không có vai trò như một áp suất âm, đóng góp tương đối tính tổng quát của nó chống lại lực hấp dẫn thông thường, gây ra một sự giãn nở không thời gian - tức đạo hàm bậc hai của a(t) là ${\ddot {a}}$ có giá trị dương hay tương đương ${\dot {a}}$ tăng theo thời gian t.

Ngoài ra, cũng trong phương trình (9) cả mật độ năng lượng $\rho$ và áp suất $p$ là nguyên nhân gây tốc độ giãn nở của vũ trụ ${\dot {a}}$ giảm dần, tức là cả hai làm giảm tốc sự giãn nở của vũ trụ. Đây là hệ quả của lực hấp dẫn, với áp suất đóng vai trò tương tự như của mật năng lượng (hay khối lượng), theo như các nguyên lý của thuyết tương đối rộng. Mặt khác, hằng số vũ trụ, khi có giá trị lấn át mật độ năng lượng và áp suất gây ra sự giãn nở gia tốc của vũ trụ.

Chứng cứ quan sát

Hiện nay chứng cứ về vũ trụ giãn nở gia tốc là rất mạnh, với nhiều thí nghiệm khác nhau trên quy mô về thời gian vũ trụ, khoảng cách vũ trụ và những quá trình vật lý, tất cả đều ủng hộ mô hình vũ trụ học ΛCDM, trong đó vũ trụ là phẳng và thành phần mật độ năng lượng là 4,9% vật chất baryon, 26,8% vật chất tối, và năng lượng tối chiếm 68,9%. Chi tiết và tham khảo tại bài viết tổng quan

Kết quả quan sát quan trọng đưa hằng số vũ trụ học trở thành một chủ đề nóng trong vật lý hiện đại đó là sự phát hiện ra các siêu tân tinh loại Ia ở xa (0<z<1), mà các nhà thiên văn coi như những ngọn nến chuẩn, có độ sáng mờ hơn so với dự định nếu vũ trụ đang giãn nở giảm tốc. Kể từ đó nhiều nhóm nhà thiên văn đã xác nhận kết quả này với thêm nhiều siêu tân tinh ở những độ dịch chuyển đỏ lớn hơn. Sự quan trọng bậc nhất đó là khi quan sát các siêu tân tinh ở dịch chuyển đỏ lớn (z>1) chúng lại có độ sáng lớn hơn so với dự định, mà đây là dấu hiệu thực nghiệm mà được chờ đợi có từ giai đoạn giảm giãn nở trước giai đoạn giãn nở gia tốc hiện nay. Những siêu tân tinh có độ dịch chuyển đỏ lớn hơn so với dự định cho phép chúng ta loại bỏ được những hiệu ứng làm mờ độ sáng của siêu tân ngoài sự giãn nở gia tốc của không thời gian trong vũ trụ.

Trước khi có kết quả công bố năm 1998 từ việc quan sát siêu tân tinh, đã có một số chứng cứ ủng hộ cho sự chấp nhận khá nhanh về vũ trụ giãn nở gia tốc từ kết quả quan sát siêu tân tinh ở xa. Có ba sự kiện trong số chúng bao gồm:

Tuổi và số phận sau cùng của vũ trụ có thể xác định bằng cách đo hằng số Hubble theo thời điểm ngày nay và ngoại suy giá trị thu được của tham số giảm tốc, được đặc trưng duy nhất bởi tham số mật độ (Ω_M cho vật chất tối và baryon và Ω_Λ cho năng lượng tối). "Vũ trụ đóng" có Ω_M > 1 và Ω_Λ = 0 kết thúc bằng Vụ Co Lớn và có tuổi trẻ hơn đáng kể so với tuổi từ tham số Hubble. "Vũ trụ mở" với Ω_M ≤ 1 và Ω_Λ = 0 sẽ giãn nở mãi mãi và có tuổi gần bằng với tuổi theo tham số Hubble. Đối với vũ trụ gia tốc với Ω_Λ khác 0 mà chúng ta đang ở trong nó (trong hình tương ứng với giá trị quan sát được Ω_M = 0,3 và Ω_Λ = 0,7), tuổi của vũ trụ rất sát với tuổi theo hằng số Hubble.

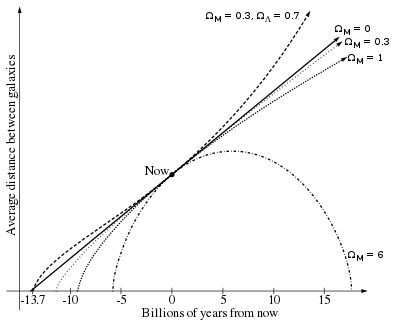
• Tuổi của Vũ trụ dường như ít hơn so với những sao già nhất từng phát hiện. Chúng ta đã khá rõ quá trình tiến hóa sao, và khi theo dõi các sao trong những cụm sao cầu và thiên hà gần cho thấy một số có tuổi trên 13 tỷ năm. Chúng ta có thể so sánh giá trị này với tuổi của vũ trụ bằng cách đo tốc độ giãn nở của vũ trụ ngày nay và lần theo trở lại tới thời điểm của Vụ Nổ Lớn. Nếu vũ trụ giãn nở giảm tốc tới tốc độ hiện tại thì tuổi của nó phải thấp hơn so với vũ trụ đang giãn nở gia tốc với tốc độ hiện tại (hình bên cạnh, tương ứng với các mô hình vũ trụ chỉ có vật chất tối và baryon, hay Ω_M > 0). Vũ trụ phẳng chỉ chứa vật chất có tuổi chỉ khoảng 9 tỷ năm - trẻ hơn vài tỷ năm so với những ngôi sao già nhất. Mặt khác, vũ trụ phẳng với thành phần chứa khoảng 70% năng lượng tối có tuổi ước tính bằng 13,8 tỷ năm. Do đó các quan sát về vũ trụ giãn nở gia tốc đã giải được nghịch lý tuổi của các ngôi sao già nhất.

• Có quá nhiều thiên hà nằm ở xa. Phương pháp đếm số lượng các thiên hà đã được các nhà thiên văn sử dụng rộng rãi để ước lượng sự giãn nở giảm tốc của vũ trụ. Thể tích không gian giữa hai khoảng cách có giá trị dịch chuyển đỏ khác nhau phụ thuộc vào lịch sử giãn nở của vũ trụ (đối với một góc khối cho trước). Khi sử dụng thể tích không gian giữa hai giá trị dịch chuyển đỏ như là hàm số của số lượng thiên hà chứa trong thể tích, các nhà thiên văn nhận thấy thể tích ở xa đo được (bằng cách đếm số thiên hà) dường như quá lớn so với thể tích tiên đoán từ mô hình vũ trụ giãn nở giảm tốc. Như vậy hoặc là độ sáng của các thiên hà hay số lượng các thiên hà trong một đơn vị thể tích đã tiến hóa theo thời gian theo cách bất ngờ nào đó, hoặc là việc tính toán thể tích dựa trên những giả thiết chưa đúng. Mô hình vũ trụ giãn nở gia tốc đã lý giải được kết quả quan sát này mà không cần tới mô hình tiến hóa thiên hà kỳ lạ nào.
• Hình học của vũ trụ là phẳng mặc dù không đủ vật chất theo như tính toán. Khi đo thăng giáng nhiệt (giữa hai điểm nóng và điểm lạnh) trong bức xạ nền vi sóng vũ trụ (CMB) phát ra khi vũ trụ ~380.000 năm tuổi, tam giác tạo thành bởi điểm quan sát từ Trái Đất và hai điểm nóng và điểm lạnh có tổng các góc xấp xỉ 180°, và có thể kết luận rằng hình học của vũ trụ là phẳng. Bằng cách kết hợp những dữ liệu này với đo lường chính xác về H₀ (dựa trên dịch chuyển đỏ của các thiên hà chằng hạn) và hoặc đo lường về mật độ vật chất trong vũ trụ (chẳng hạn xác định khối lượng và độ sáng của các đám thiên hà, dựa trên thấu kính hấp dẫn hoặc phổ công suất của CMB), các nhà thiên văn nhận thấy rõ ràng rằng mật độ vật chất trong vũ trụ chỉ đóng góp vào khoảng 30% tổng thành phần trong nó. Một cách để tính tới mật độ năng lượng bị thiếu đó là đưa vào một hằng số vũ trụ học. Và như kết quả quan sát được, giá trị hằng số vũ trụ học đo được cần để giải thích sự giãn nở gia tốc quan sát thấy từ dữ liệu siêu tân tinh, là đủ và phù hợp để làm cho hình học của vũ trụ là phẳng. Do vậy hằng số vũ trụ học lý giải được sự mâu thuẫn giữa mật độ vật chất với các thí nghiệm quan sát từ CMB.

Những vấn đề chưa giải được

Mặc dù có những thành công về mặt mô hình đơn giản, hằng số vũ trụ học cũng như năng lượng tối vẫn chưa thể giải thích được một số vấn đề trong vật lý học (chi tiết xem).

Vấn đề giá trị năng lượng chân không

Một trong những thử thách lớn nhất của vật lý học ngày nay đó là giải thích giá trị dương nhỏ của hằng số vũ trụ học, hay một cách tương đương, mật độ năng lượng chân không. Giá trị đo được bởi quan sát vũ trụ học $\rho _{\Lambda }$ ~ 7x10⁻³⁰ g/cm³, nhỏ hơn 120 bậc độ lớn so với mật độ Planck tính theo phương pháp phân tích thứ nguyên và lý thuyết trường hữu hiệu bằng 10⁹³ g/cm³, giá trị được tính tại lúc Vũ trụ hình thành từ thời điểm Vụ Nổ Lớn. Càng khó hiểu hơn, mật độ chân không thu được từ các đóng góp bởi những hiệu ứng vật lý năng lượng thấp hơn, bao gồm sự chuyển tiếp pha điện yếu (QED) và sắc động lực học lượng tử (QCD), chỉ trở lên quan trọng ở những thời điểm muộn hơn. Các nhà vật lý ngày nay giải thích giá trị rất nhỏ này đòi hỏi một cơ chế có khả năng hủy rất nhiều những đóng góp khác nhau với độ chính xác gần tuyệt đối.

Cách giải thích dựa trên nguyên lý vị nhân

Một cách để giải thích giá trị nhỏ nhưng khác không của năng lượng chân không đưa ra bởi Steven Weinberg vào năm 1987 dựa trên nguyên lý vị nhân. Weinberg giải thích rằng nếu năng lượng chân không có những giá trị khác nhau ở trong những miền khác nhau của Vũ trụ, thì nếu tồn tại một nền văn minh ngoài vũ trụ thì họ sẽ đo được giá trị năng lượng chân không tương ứng trong miền đó: những cấu trúc hỗ trợ cho sự hình thành sự sống sẽ không tồn tại được trong những miền có giá trị năng lượng chân không lớn hơn. Cụ thể, nếu năng lượng chân không là âm và giá trị tuyệt đối của nó lớn hơn so với giá trị quan sát được ngày nay (chẳng hạn 10 lần lớn hơn), và giữ cho những tham số khác không đổi (ví dụ mật độ vật chất), thì tô pô của Vũ trụ là đóng; hơn nữa tuổi của nó sẽ ngắn hơn so với tuổi của Vũ trụ hiện nay, và có thể quá ngắn để hình thành sự sống có trí tuệ. Mặt khác, nếu một vũ trụ có hằng số vũ trụ học là dương thì nó sẽ giãn nở quá nhanh, cản trở các thiên hà hình thành. Theo Weinberg, những miền nơi hằng số vũ trụ tương thích cho sự sống có thể là rất hiếm. Bằng lập luận này, ông tiên đoán rằng hằng số vũ trụ học có giá trị nhỏ hơn 100 lần giá trị được chấp nhận hiện nay. Năm 1992, Weinberg thu được giá trị hằng số vũ trụ gấp 5 đến 10 lần mật độ vật chất.

Những mô hình khác

Lý thuyết đa vũ trụ đưa ra nhiều "vũ trụ song song" cùng tồn tại với những giá trị hằng số và định luật vật lý khác nhau trong đó có hằng số vũ trụ. Và cũng tương tự như nguyên lý vị nhân, chúng ta chỉ có thể sống trong một vũ trụ có những điều kiện tương thích để hình thành sự sống.

Lý thuyết dây cũng như thuyết M với mục tiêu thống nhất mọi lực trong tự nhiên đưa ra cách giải thích cho giá trị các hằng số vật lý, nhưng hai lý thuyết tiên đoán khá nhiều mô hình vũ trụ và vũ trụ của chúng ta chỉ là một trong số đó.

Có thể năng lượng tối không phải là một thành phần năng lượng trong vũ trụ, mà là ở các phương trình của thuyết tương đối cần sửa đổi dạng của chúng. Theo cách này, các nhà vật lý sửa đổi hoặc là ở vế hình học của phương trình trường Einstein hoặc họ bổ sung thêm số hạng vào tenxơ năng lượng xung lượng. Nó cũng tương tự như lý thuyết của Newton là trường hợp giới hạn của thuyết tương đối rộng khi ở trường hấp dẫn yếu và vận tốc nhỏ.

Thư mục tham khảo

• Carroll, Sean; Press, William; Turner, Edwin (1992), The cosmological constant, 30, Annual Review of Astronomy and Astrophysics, tr. 499–542, doi:10.1146/annurev.aa.30.090192.002435
• Carroll, Sean (2001), The cosmological constant, 4, Living Reviews in Relativity, doi:10.12942/lrr-2001-1
• Carroll, Sean (2004), Spacetime and Geometry, Addison Wesley, San Francisco, CA, tr. 171-174, ISBN 978-0805387322
• Einstein, Albert (1917), Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie, Koniglich Preußische Akademie der Wissenschaften, Sitzungsberichte (Berlin), tr. 142-152, Bibcode:1917SPAW.......142E

• For an English translation see Einstein, Albert (1997). The collected papers of Albert Einstein (Alfred Engel, translator) Princeton University Press, Princeton, New Jersey.

• Einstein, Albert (1931), Zum Kosmologischen Problem der allgemeinen Relativitätstheorie, Sitzungsberichte Preussische Akademie der Wissenschaften, Berlin
• Friedmann, Alexander (1922), Über die Krümmung des Raumes, 10, Zeitschrift für Physik, tr. 377–386, Bibcode:1922ZPhy...10..377F, doi:10.1007/BF01332580

• For an English translation see Friedmann, Alexander (1999). Gen. Rel. Grav. 31: 1991-2000.

• Frieman, Joshua; Turner, Michael; Huterer, Dragan (2008), Dark Energy and the Accelerating Universe, 46, Annual Review of Astronomy and Astrophysics, tr. 385–432, arXiv:0803.0982, doi:10.1146/annurev.astro.46.060407.145243
• Gamow, George (1970), My World Line, Viking, New York, tr. 44
• Padmanabhan, Thanu (2003), Cosmological constant - The weight of the vacuum, 380, Physics Reports, tr. 235–320, arXiv:hep-th/0212290v2, doi:10.1016/S0370-1573(03)00120-0
• Pais, Abraham (1982), 'Subtle is the Lord...' The Science and life of Albert Einstein, Oxford University Press, ISBN 0-19-853907-X
• Perlmutter, Saul (1999), Measurements of Ω and Λ from 42 high-redshift supernovae, 517, The Astrophysical Journal, tr. 565-586, arXiv:astro-ph/9812133v1, doi:10.1086/307221
• Polchinski, Joseph (2006), The cosmological constant and the string landscape, arXiv:hep-th/0603249
• Riess, Adam (1998), Observational evidence from supernovae for an accelerating universe and a cosmological constant, 116, The Astrophysical Journal, tr. 1009-1038, arXiv:astro-ph/9805201v1, doi:10.1086/300499
• Weinberg, Steven (1989), The cosmological constant problem, 61, Reviews of Modern Physics, tr. 1-23, doi:10.1103/RevModPhys.61.1
• Weinberg, Steven (2000), The cosmological constant problems, arXiv:astro-ph/0005265v1
• de Sitter, Willem (1917), On the relativity of inertia. Remarks concerning Einstein's latest hypothesis, 19, Koninklijke Nederlandsche Akademie van Wetenschappen Proceedings, tr. 1217-1225, Bibcode:1917KNAB...19.1217D

Liên kết ngoài

• Cosmological constant (astronomy) tại Encyclopædia Britannica (tiếng Anh)
• Carroll, Sean M, "The Cosmological Constant" (short), "The Cosmological Constant" Lưu trữ 2016-08-29 tại Wayback Machine(extended). Pdf Lưu trữ 2014-11-02 tại Wayback Machine
• 'Cyclic universe' can explain cosmological constant. New Scientist 19:00 ngày 4 tháng 5 năm 2006 by Zeeya Merali doi:10.1126/science.1126231
• Mysterious force's long presence BBC Last Updated: Thursday, ngày 16 tháng 11 năm 2006, 22:59 GMT
• Einstein's Biggest Blunder - American Physical Society